Code
source("../dsan-globals/_globals.r")DSAN 5000: Data Science and Analytics
source("../dsan-globals/_globals.r")\[ \DeclareMathOperator*{\argmax}{argmax} \DeclareMathOperator*{\argmin}{argmin} \newcommand{\bigexp}[1]{\exp\mkern-4mu\left[ #1 \right]} \newcommand{\bigexpect}[1]{\mathbb{E}\mkern-4mu \left[ #1 \right]} \newcommand{\definedas}{\overset{\text{defn}}{=}} \newcommand{\definedalign}{\overset{\phantom{\text{defn}}}{=}} \newcommand{\eqeventual}{\overset{\text{eventually}}{=}} \newcommand{\expect}[1]{\mathbb{E}[#1]} \newcommand{\expectsq}[1]{\mathbb{E}^2[#1]} \newcommand{\fw}[1]{\texttt{#1}} \newcommand{\given}{\mid} \newcommand{\green}[1]{\color{green}{#1}} \newcommand{\heads}{\outcome{heads}} \newcommand{\lik}{\mathcal{L}} \newcommand{\mle}{\textsf{ML}} \newcommand{\orange}[1]{\color{orange}{#1}} \newcommand{\outcome}[1]{\textsf{#1}} \newcommand{\param}[1]{{\color{purple} #1}} \newcommand{\paramDist}{\param{\boldsymbol\theta_\mathcal{D}}} \newcommand{\pgsamplespace}{\{\green{1},\green{2},\green{3},\purp{4},\purp{5},\purp{6}\}} \newcommand{\prob}[1]{P\left( #1 \right)} \newcommand{\purp}[1]{\color{purple}{#1}} \newcommand{\spacecap}{\; \cap \;} \newcommand{\spacewedge}{\; \wedge \;} \newcommand{\tails}{\outcome{tails}} \newcommand{\Var}[1]{\text{Var}[#1]} \newcommand{\bigVar}[1]{\text{Var}\mkern-4mu \left[ #1 \right]} \]
| General Questions | Specific Questions |
|---|---|
| Is it a physical object? | Is it a soda can? |
| Is it an animal? | Is it a cat? |
| Is it bigger than a house? | Is it a planet? |
For linguistics fans: if a word \(x\) is one level “more general” than another word \(y\) (e.g., the word “camel” is one level more general than “bactrian camel”, a camel with two humps), we say that \(x\) is a hypernym of \(y\), and that \(y\) is a hyponym of \(x\). The WordNet project is a big tree of hypernym/hyponym relationships among all English words, where “entity” is the root node of the tree.
| \(\text{Choice}\) | Tree | Bird | Car |
| \(\Pr(\text{Choice})\) | 0.25 | 0.25 | 0.50 |
Example adapted from this essay by Simon DeDeo!
\[ \begin{align*} &\mathbb{E}[\text{\# Moves}] \\ =\,&1 \cdot \Pr(\text{Car}) + 2 \cdot \Pr(\text{Bird}) \\ &+ 2 \cdot \Pr(\text{Tree}) \\ =\,&1 \cdot 0.5 + 2\cdot 0.25 + 2\cdot 0.25 \\ =\,&1.5 \end{align*} \]
\[ \begin{align*} &\mathbb{E}[\text{\# Moves}] \\ =\,&1 \cdot \Pr(\text{Bird}) + 2 \cdot \Pr(\text{Car}) \\ &+ 2 \cdot \Pr(\text{Tree}) \\ =\,&1 \cdot 0.25 + 2\cdot 0.5 + 2\cdot 0.25 \\ =\,&1.75 \end{align*} \]
\[ \begin{align*} &\mathbb{E}[\text{\# Moves}] \\ =\,&1 \cdot \Pr(\text{Bird}) + 3 \cdot \Pr(\text{Car}) \\ &+ 3 \cdot \Pr(\text{Tree}) \\ =\,&1 \cdot 0.25 + 3\cdot 0.5 + 3\cdot 0.25 \\ =\,&2.5 \end{align*} \]
\[ \begin{align*} H(X) &= -\sum_{i=1}^N \Pr(X = i)\log_2\Pr(X = i) \end{align*} \]
\[ \begin{align*} H(X) &= -\left[ \Pr(X = \text{Car}) \log_2\Pr(X = \text{Car}) \right. \\ &\phantom{= -[ } + \Pr(X = \text{Bird})\log_2\Pr(X = \text{Bird}) \\ &\phantom{= -[ } + \left. \Pr(X = \text{Tree})\log_2\Pr(X = \text{Tree})\right] \\ &= -\left[ (0.5)(-1) + (0.25)(-2) + (0.25)(-2) \right] = 1.5~🧐 \end{align*} \]
\[ \begin{align*} \mathbb{E}[\text{\# Moves}] &= 1 \cdot (1/3) + 2 \cdot (1/3) + 2 \cdot (1/3) \\ &= \frac{5}{3} \approx 1.667 \end{align*} \]
\[ \begin{align*} H(X) &= -\left[ \Pr(X = \text{Car}) \log_2\Pr(X = \text{Car}) \right. \\ &\phantom{= -[ } + \Pr(X = \text{Bird})\log_2\Pr(X = \text{Bird}) \\ &\phantom{= -[ } + \left. \Pr(X = \text{Tree})\log_2\Pr(X = \text{Tree})\right] \\ &= -\left[ \frac{1}{3}\log_2\left(\frac{1}{3}\right) + \frac{1}{3}\log_2\left(\frac{1}{3}\right) + \frac{1}{3}\log_2\left(\frac{1}{3}\right) \right] \approx 1.585~🧐 \end{align*} \]
The smallest possible number of levels \(L^*\) for a script based on RV \(X\) is exactly
\[ L^* = \lceil H(X) \rceil \]
Intuition: Although \(\mathbb{E}[\text{\# Moves}] = 1.5\), we cannot have a tree with 1.5 levels!
Entropy provides a lower bound on \(\mathbb{E}[\text{\# Moves}]\):
\[ \mathbb{E}[\text{\# Moves}] \geq H(X) \]
library(tidyverse)── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
✔ dplyr 1.1.4 ✔ readr 2.1.5
✔ forcats 1.0.0 ✔ stringr 1.5.1
✔ lubridate 1.9.3 ✔ tibble 3.2.1
✔ purrr 1.0.2 ✔ tidyr 1.3.1
── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
✖ dplyr::filter() masks stats::filter()
✖ dplyr::lag() masks stats::lag()
ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errorslibrary(lubridate)
set.seed(5001)
sample_size <- 100
day <- seq(ymd('2023-01-01'),ymd('2023-12-31'),by='weeks')
lat_bw <- 5
latitude <- seq(-90, 90, by=lat_bw)
ski_df <- expand_grid(day, latitude)
#ski_df |> head()
# Data-generating process
lat_cutoff <- 35
ski_df <- ski_df |> mutate(
near_equator = abs(latitude) <= lat_cutoff,
northern = latitude > lat_cutoff,
southern = latitude < -lat_cutoff,
first_3m = day < ymd('2023-04-01'),
last_3m = day >= ymd('2023-10-01'),
middle_6m = (day >= ymd('2023-04-01')) & (day < ymd('2023-10-01')),
snowfall = 0
)
# Update the non-zero sections
mu_snow <- 10
sd_snow <- 2.5
# How many northern + first 3 months
num_north_first_3 <- nrow(ski_df[ski_df$northern & ski_df$first_3m,])
ski_df[ski_df$northern & ski_df$first_3m, 'snowfall'] = rnorm(num_north_first_3, mu_snow, sd_snow)
# Northerns + last 3 months
num_north_last_3 <- nrow(ski_df[ski_df$northern & ski_df$last_3m,])
ski_df[ski_df$northern & ski_df$last_3m, 'snowfall'] = rnorm(num_north_last_3, mu_snow, sd_snow)
# How many southern + middle 6 months
num_south_mid_6 <- nrow(ski_df[ski_df$southern & ski_df$middle_6m,])
ski_df[ski_df$southern & ski_df$middle_6m, 'snowfall'] = rnorm(num_south_mid_6, mu_snow, sd_snow)
# And collapse into binary var
ski_df['good_skiing'] = ski_df$snowfall > 0
# This converts day into an int
ski_df <- ski_df |> mutate(
day_num = lubridate::yday(day)
)
#print(nrow(ski_df))
ski_sample <- ski_df |> slice_sample(n = sample_size)
ski_sample |> write_csv("assets/ski.csv")
ggplot(
ski_sample,
aes(
x=day,
y=latitude,
#shape=good_skiing,
color=good_skiing
)) +
geom_point(
size = g_pointsize / 1.5,
#stroke=1.5
) +
dsan_theme() +
labs(
x = "Time of Year",
y = "Latitude",
shape = "Good Skiing?"
) +
scale_shape_manual(name="Good Skiing?", values=c(1, 3)) +
scale_color_manual(name="Good Skiing?", values=c(cbPalette[1], cbPalette[2]), labels=c("No (Sunny)","Yes (Snowy)")) +
scale_x_continuous(
breaks=c(ymd('2023-01-01'), ymd('2023-02-01'), ymd('2023-03-01'), ymd('2023-04-01'), ymd('2023-05-01'), ymd('2023-06-01'), ymd('2023-07-01'), ymd('2023-08-01'), ymd('2023-09-01'), ymd('2023-10-01'), ymd('2023-11-01'), ymd('2023-12-01')),
labels=c("Jan", "Feb", "Mar", "Apr", "May", "Jun", "Jul", "Aug", "Sep", "Oct", "Nov", "Dec")
) +
scale_y_continuous(breaks=c(-90, -60, -30, 0, 30, 60, 90))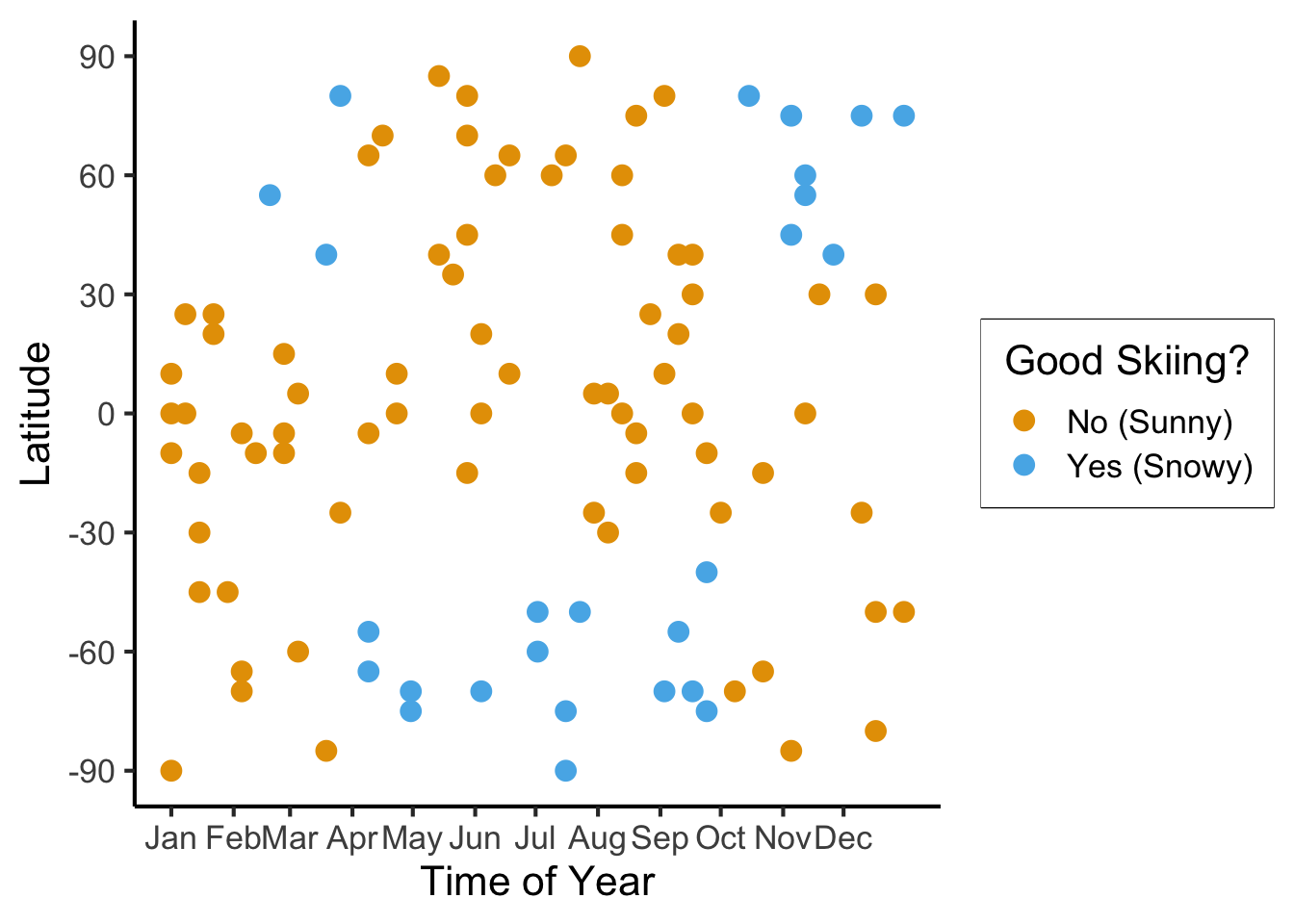
ski_sample |> count(good_skiing)| good_skiing | n |
|---|---|
| FALSE | 74 |
| TRUE | 26 |
\[ \mathscr{L}(R_i) = -\sum_{c}\widehat{p}_c(R_i)\log_2(\widehat{p}_c(R_i)) \]
\[ \mathscr{L}(R_i) = -[(0.74)\log_2(0.74) + (0.26)\log_2(0.26)] \approx 0.827 \]
Let’s think through two choices for the first split:
ski_sample <- ski_sample |> mutate(
lat_lt_475 = latitude <= 47.5
)
ski_sample |> group_by(lat_lt_475) |> count(good_skiing)
ski_sample <- ski_sample |> mutate(
month_lt_oct = day < ymd('2023-10-01')
)
ski_sample |> group_by(month_lt_oct) |> count(good_skiing)\(\text{latitude} \leq -47.5\):
| lat_lt_475 | good_skiing | n |
|---|---|---|
| FALSE | FALSE | 13 |
| FALSE | TRUE | 8 |
| TRUE | FALSE | 61 |
| TRUE | TRUE | 18 |
This gives us the rule
\[ \widehat{C}(x) = \begin{cases} 0 &\text{if }\text{latitude} \leq 47.5, \\ 0 &\text{otherwise} \end{cases} \]
\(\text{month} < \text{October}\)
| month_lt_oct | good_skiing | n |
|---|---|---|
| FALSE | FALSE | 12 |
| FALSE | TRUE | 8 |
| TRUE | FALSE | 62 |
| TRUE | TRUE | 18 |
This gives us the rule
\[ \widehat{C}(x) = \begin{cases} 0 &\text{if }\text{month} < \text{October}, \\ 0 &\text{otherwise} \end{cases} \]
So, if we judge purely on acuracy scores… it seems like we’re not getting anywhere here (but, we know we are getting somewhere!)
import json
import pandas as pd
import numpy as np
import sklearn
from sklearn.tree import DecisionTreeClassifier
sklearn.set_config(display='text')
ski_df = pd.read_csv("assets/ski.csv")
ski_df['good_skiing'] = ski_df['good_skiing'].astype(int)
X = ski_df[['day_num', 'latitude']]
y = ski_df['good_skiing']
dtc = DecisionTreeClassifier(
max_depth = 1,
criterion = "entropy",
random_state=5001
)
dtc.fit(X, y);
y_pred = pd.Series(dtc.predict(X), name="y_pred")
result_df = pd.concat([X,y,y_pred], axis=1)
result_df['correct'] = result_df['good_skiing'] == result_df['y_pred']
result_df.to_csv("assets/ski_predictions.csv")
sklearn.tree.plot_tree(dtc, feature_names = X.columns)
n_nodes = dtc.tree_.node_count
children_left = dtc.tree_.children_left
children_right = dtc.tree_.children_right
feature = dtc.tree_.feature
feat_index = feature[0]
feat_name = X.columns[feat_index]
thresholds = dtc.tree_.threshold
feat_threshold = thresholds[0]
#print(f"Feature: {feat_name}\nThreshold: <= {feat_threshold}")
values = dtc.tree_.value
#print(values)
dt_data = {
'feat_index': feat_index,
'feat_name': feat_name,
'feat_threshold': feat_threshold
}
dt_df = pd.DataFrame([dt_data])
dt_df.to_feather('assets/ski_dt.feather')
library(tidyverse)
library(arrow)
# Load the dataset
ski_result_df <- read_csv("assets/ski_predictions.csv")
# Load the DT info
dt_df <- read_feather("assets/ski_dt.feather")
# Here we only have one value, so just read that
# value directly
lat_thresh <- dt_df$feat_threshold
ggplot(ski_result_df, aes(x=day_num, y=latitude, color=factor(good_skiing), shape=correct)) +
geom_point(
size = g_pointsize / 1.5,
stroke = 1.5
) +
geom_hline(
yintercept = lat_thresh,
linetype = "dashed"
) +
dsan_theme("half") +
labs(
x = "Time of Year",
y = "Latitude",
color = "True Class",
#shape = "Correct?"
) +
scale_shape_manual("DT Prediction", values=c(1,3), labels=c("Incorrect","Correct")) +
scale_color_manual("True Class", values=c(cbPalette[1], cbPalette[2]), labels=c("Bad (Sunny)","Good (Snowy)"))
ski_result_df |> count(correct)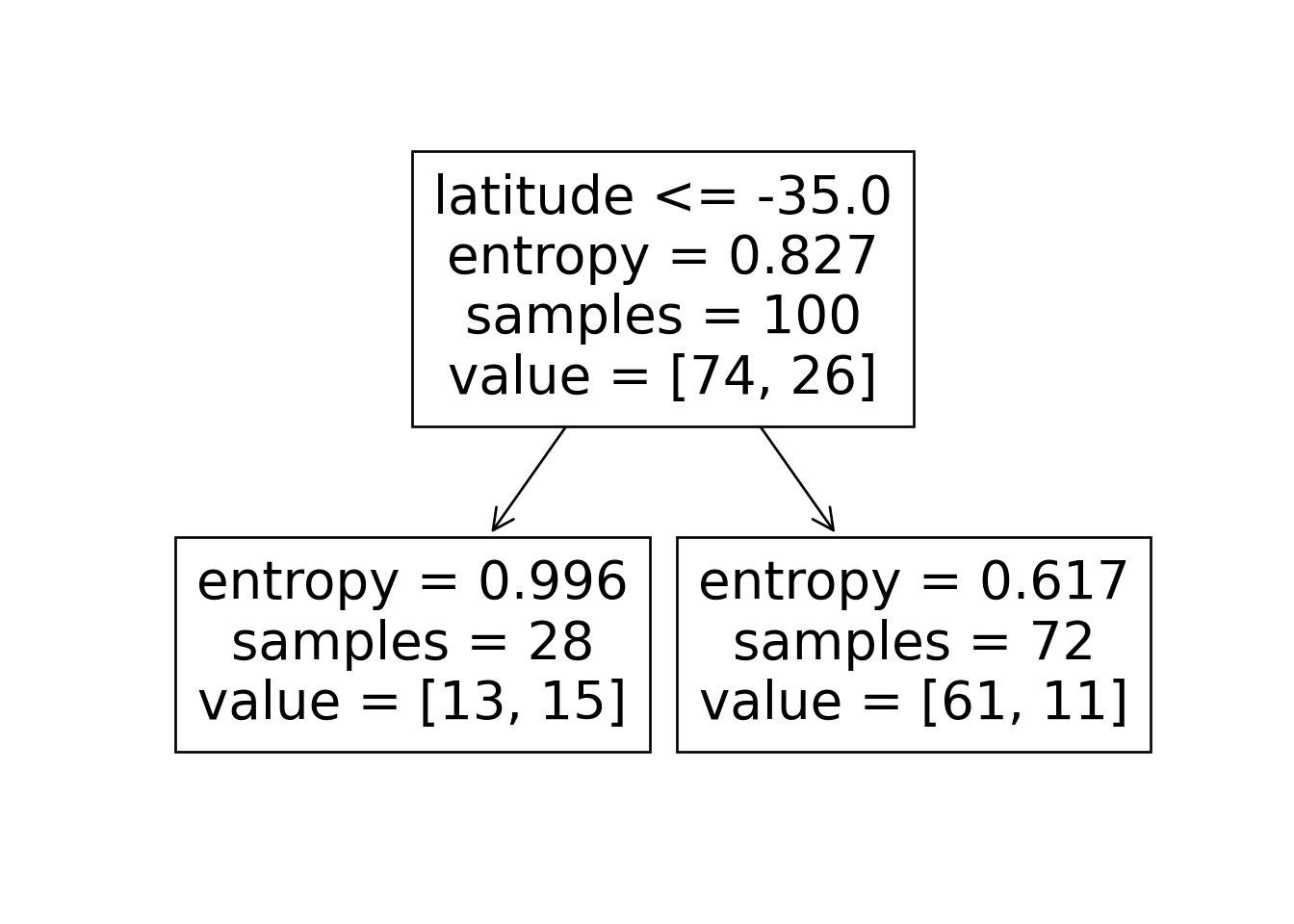
Attaching package: 'arrow'The following object is masked from 'package:lubridate':
durationThe following object is masked from 'package:utils':
timestampNew names:
• `` -> `...1`Rows: 100 Columns: 6
── Column specification ────────────────────────────────────────────────────────
Delimiter: ","
dbl (5): ...1, day_num, latitude, good_skiing, y_pred
lgl (1): correct
ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.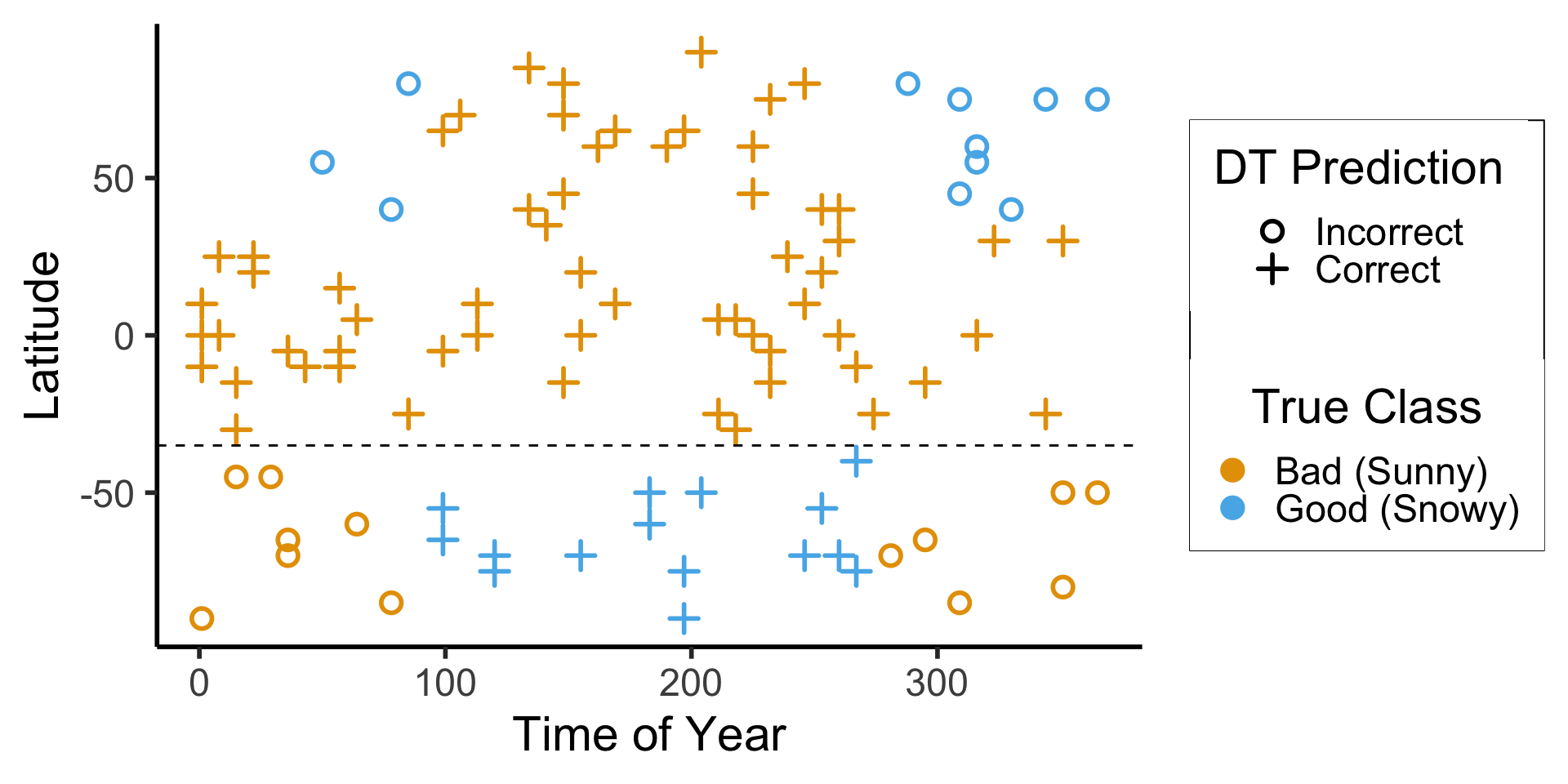
| correct | n |
|---|---|
| FALSE | 24 |
| TRUE | 76 |
\[ \begin{align*} \mathscr{L}(R_1) &= -\left[ \frac{13}{28}\log_2\left(\frac{13}{28}\right) + \frac{15}{28}\log_2\left(\frac{15}{28}\right) \right] \approx 0.996 \\ \mathscr{L}(R_2) &= -\left[ \frac{61}{72}\log_2\left(\frac{61}{72}\right) + \frac{11}{72}\log_2\left(\frac{11}{72}\right) \right] \approx 0.617 \\ %\mathscr{L}(R \rightarrow (R_1, R_2)) &= \Pr(x_i \in R_1)\mathscr{L}(R_1) + \Pr(x_i \in R_2)\mathscr{L}(R_2) \\ \mathscr{L}(R_1, R_2) &= \frac{28}{100}(0.996) + \frac{72}{100}(0.617) \approx 0.723 < 0.827~😻 \end{align*} \]
#format_snow <- function(x) sprintf('%.2f', x)
format_snow <- function(x) round(x, 2)
ski_sample['snowfall_str'] <- sapply(ski_sample$snowfall, format_snow)
#ski_df |> head()
#print(nrow(ski_df))
ggplot(ski_sample, aes(x=day, y=latitude, label=snowfall_str)) +
geom_text(size = 6) +
dsan_theme() +
labs(
x = "Time of Year",
y = "Latitude",
shape = "Good Skiing?"
) +
scale_shape_manual(values=c(1, 3)) +
scale_x_continuous(
breaks=c(ymd('2023-01-01'), ymd('2023-02-01'), ymd('2023-03-01'), ymd('2023-04-01'), ymd('2023-05-01'), ymd('2023-06-01'), ymd('2023-07-01'), ymd('2023-08-01'), ymd('2023-09-01'), ymd('2023-10-01'), ymd('2023-11-01'), ymd('2023-12-01')),
labels=c("Jan", "Feb", "Mar", "Apr", "May", "Jun", "Jul", "Aug", "Sep", "Oct", "Nov", "Dec")
) +
scale_y_continuous(breaks=c(-90, -60, -30, 0, 30, 60, 90))
library(tidyverse)
library(latex2exp)
expr_pi2 <- TeX("$\\frac{\\pi}{2}$")
expr_pi <- TeX("$\\pi$")
expr_3pi2 <- TeX("$\\frac{3\\pi}{2}$")
expr_2pi <- TeX("$2\\pi$")
x_range <- 2 * pi
x_coords <- seq(0, x_range, by = x_range / 100)
num_x_coords <- length(x_coords)
data_df <- tibble(x = x_coords)
data_df <- data_df |> mutate(
y_raw = sin(x),
y_noise = rnorm(num_x_coords, 0, 0.15)
)
data_df <- data_df |> mutate(
y = y_raw + y_noise
)
#y_coords <- y_raw_coords + y_noise
#y_coords <- y_raw_coords
#data_df <- tibble(x = x, y = y)
reg_tree_plot <- ggplot(data_df, aes(x=x, y=y)) +
geom_point(size = g_pointsize / 2) +
dsan_theme("half") +
labs(
x = "Feature",
y = "Label"
) +
geom_vline(
xintercept = pi,
linewidth = g_linewidth,
linetype = "dashed"
) +
scale_x_continuous(
breaks=c(0,pi/2,pi,(3/2)*pi,2*pi),
labels=c("0",expr_pi2,expr_pi,expr_3pi2,expr_2pi)
)
reg_tree_plot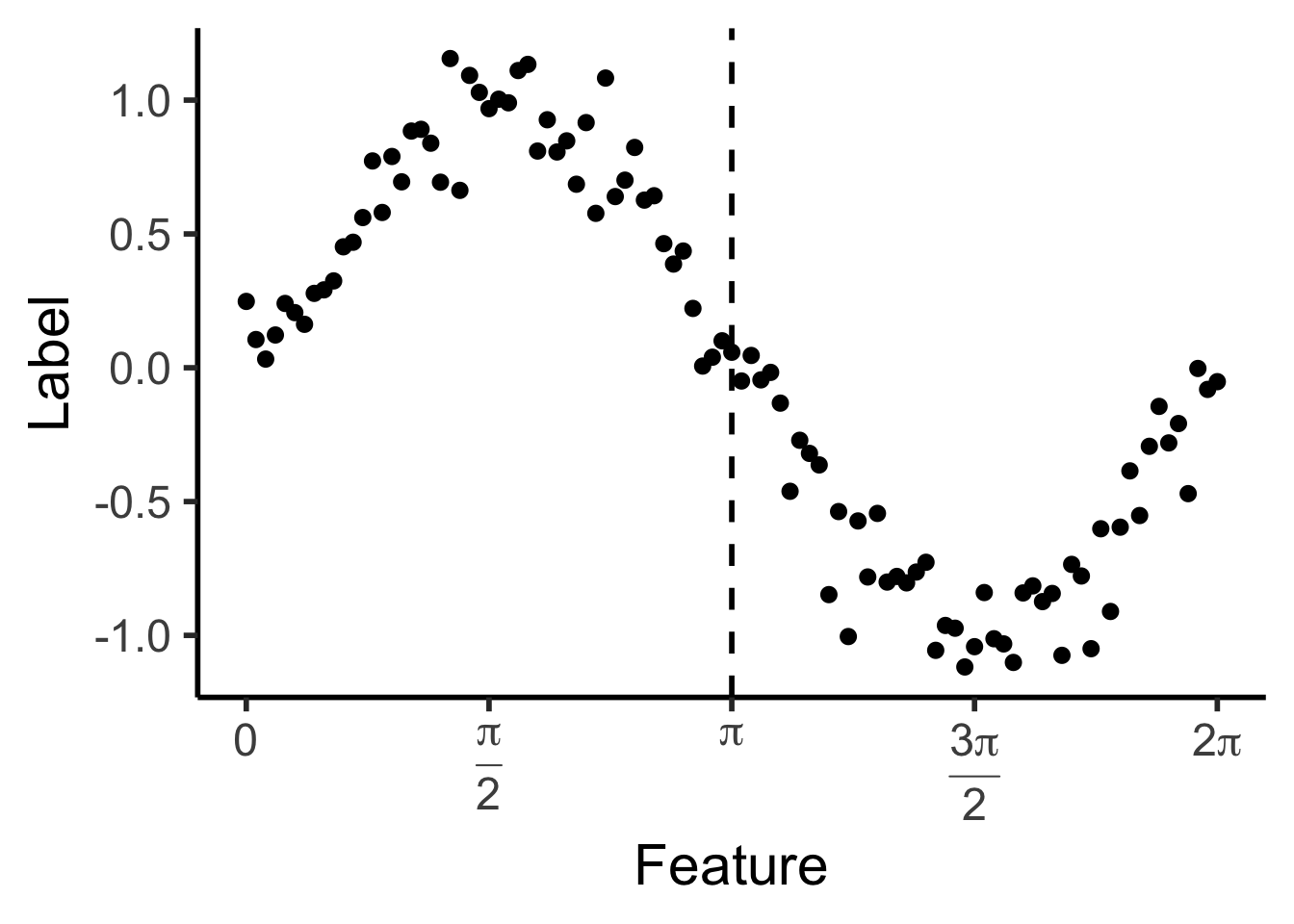
library(ggtext)
# x_lt_pi = data_df |> filter(x < pi)
# mean(x_lt_pi$y)
data_df <- data_df |> mutate(
pred_sq_err0 = (y - 0)^2
)
mse0 <- mean(data_df$pred_sq_err0)
mse0_str <- sprintf("%.3f", mse0)
reg_tree_plot +
geom_hline(
yintercept = 0,
color=cbPalette[1],
linewidth = g_linewidth
) +
geom_segment(
aes(x=x, xend=x, y=0, yend=y)
) +
geom_text(
aes(x=(3/2)*pi, y=0.5, label=paste0("MSE = ",mse0_str)),
size = 10,
#box.padding = unit(c(2,2,2,2), "pt")
)Warning in geom_text(aes(x = (3/2) * pi, y = 0.5, label = paste0("MSE = ", : All aesthetics have length 1, but the data has 101 rows.
ℹ Please consider using `annotate()` or provide this layer with data containing
a single row.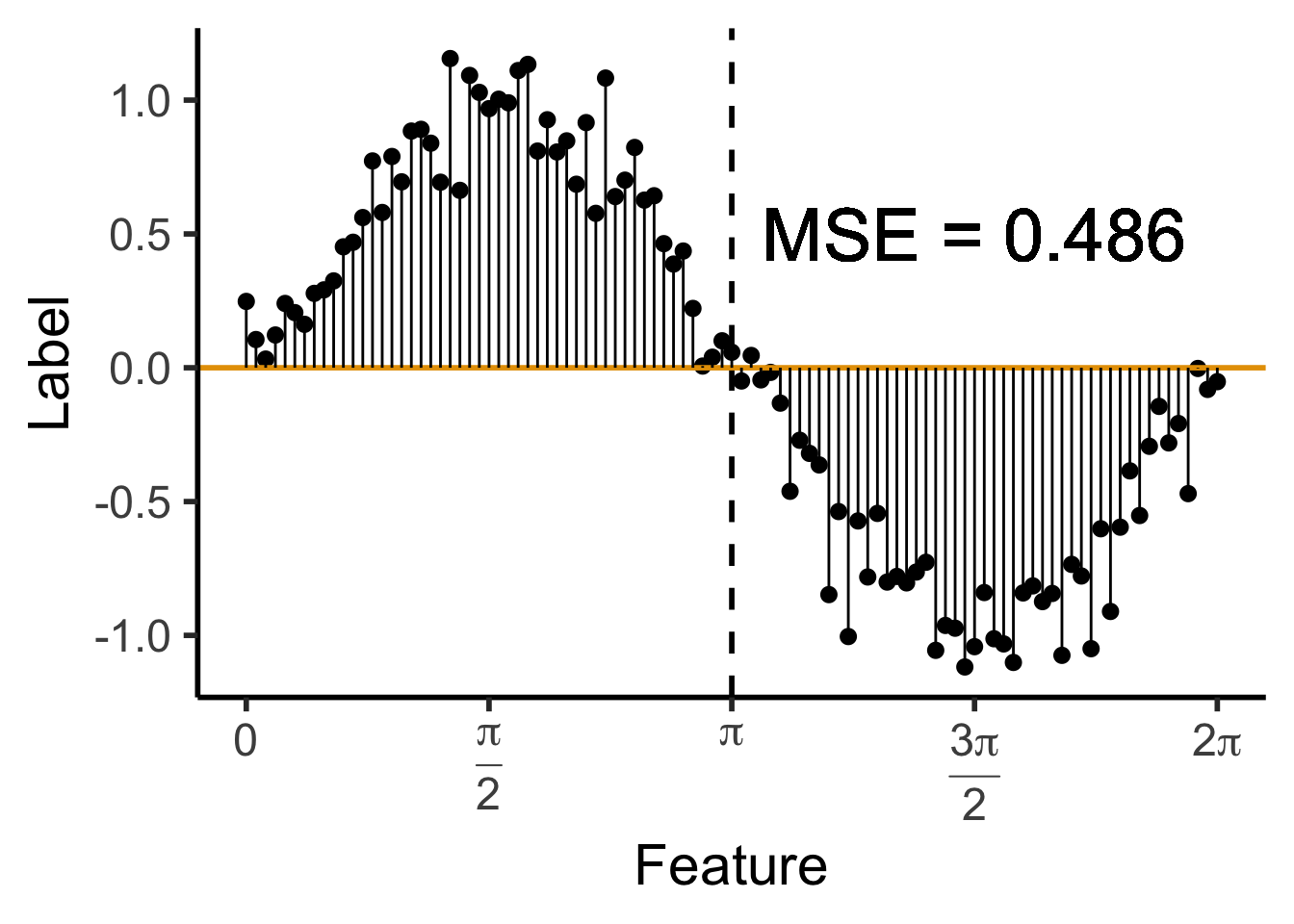
\[ \widehat{y}(x) = \begin{cases} \phantom{-}\frac{2}{\pi} &\text{if }x < \pi, \\ -\frac{2}{\pi} &\text{otherwise.} \end{cases} \]
get_y_pred <- function(x) ifelse(x < pi, 2/pi, -2/pi)
data_df <- data_df |> mutate(
pred_sq_err1 = (y - get_y_pred(x))^2
)
mse1 <- mean(data_df$pred_sq_err1)
mse1_str <- sprintf("%.3f", mse1)
decision_df <- tribble(
~x, ~xend, ~y, ~yend,
0, pi, 2/pi, 2/pi,
pi, 2*pi, -2/pi, -2/pi
)
reg_tree_plot +
geom_segment(
data=decision_df,
aes(x=x, xend=xend, y=y, yend=yend),
color=cbPalette[1],
linewidth = g_linewidth
) +
geom_segment(
aes(x=x, xend=x, y=get_y_pred(x), yend=y)
) +
geom_text(
aes(x=(3/2)*pi, y=0.5, label=paste0("MSE = ",mse1_str)),
size = 9,
#box.padding = unit(c(2,2,2,2), "pt")
)Warning in geom_text(aes(x = (3/2) * pi, y = 0.5, label = paste0("MSE = ", : All aesthetics have length 1, but the data has 101 rows.
ℹ Please consider using `annotate()` or provide this layer with data containing
a single row.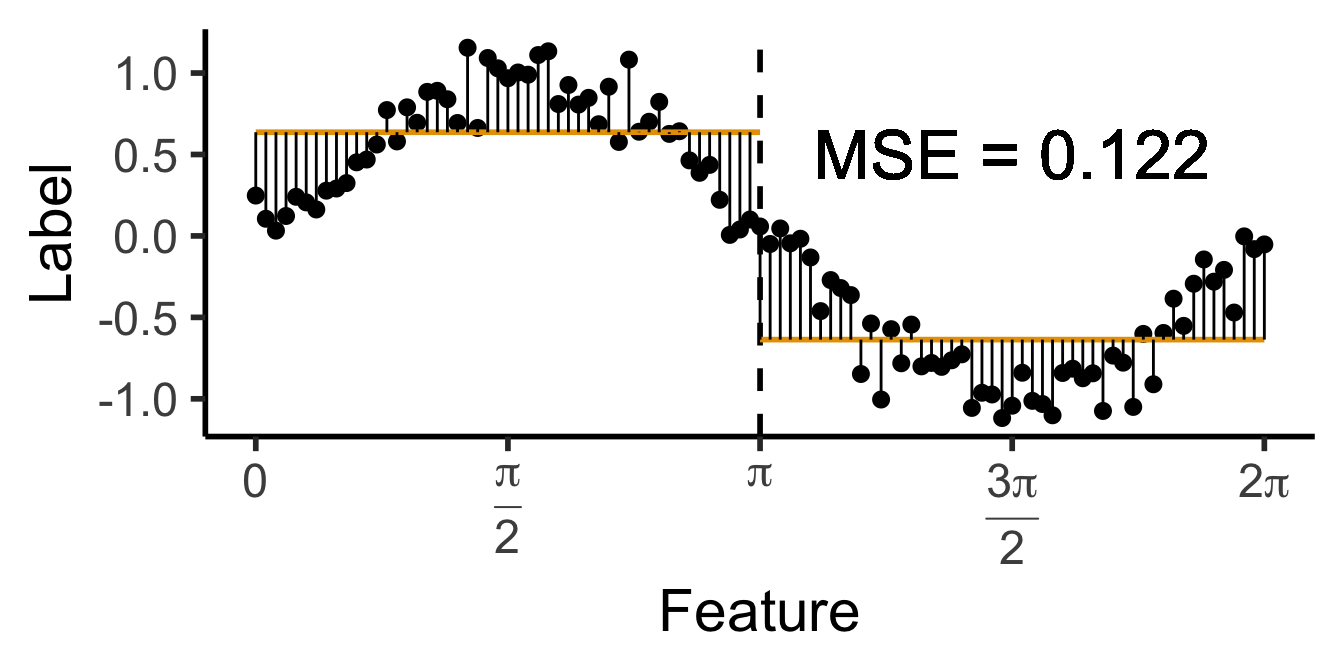
\[ \widehat{y}(x) = \begin{cases} \phantom{-}\frac{9}{4\pi} &\text{if }x < \frac{2\pi}{3}, \\ \phantom{-}0 &\text{if }\frac{2\pi}{3} \leq x \leq \frac{4\pi}{3} \\ -\frac{9}{4\pi} &\text{otherwise.} \end{cases} \]
cut1 <- (2/3) * pi
cut2 <- (4/3) * pi
pos_mean <- 9 / (4*pi)
get_y_pred <- function(x) ifelse(x < cut1, pos_mean, ifelse(x < cut2, 0, -pos_mean))
data_df <- data_df |> mutate(
pred_sq_err1b = (y - get_y_pred(x))^2
)
mse1b <- mean(data_df$pred_sq_err1b)
mse1b_str <- sprintf("%.3f", mse1b)
decision_df <- tribble(
~x, ~xend, ~y, ~yend,
0, (2/3)*pi, pos_mean, pos_mean,
(2/3)*pi, (4/3)*pi, 0, 0,
(4/3)*pi, 2*pi, -pos_mean, -pos_mean
)
reg_tree_plot +
geom_segment(
data=decision_df,
aes(x=x, xend=xend, y=y, yend=yend),
color=cbPalette[1],
linewidth = g_linewidth
) +
geom_segment(
aes(x=x, xend=x, y=get_y_pred(x), yend=y)
) +
geom_text(
aes(x=(3/2)*pi, y=0.5, label=paste0("MSE = ",mse1b_str)),
size = 9,
#box.padding = unit(c(2,2,2,2), "pt")
)Warning in geom_text(aes(x = (3/2) * pi, y = 0.5, label = paste0("MSE = ", : All aesthetics have length 1, but the data has 101 rows.
ℹ Please consider using `annotate()` or provide this layer with data containing
a single row.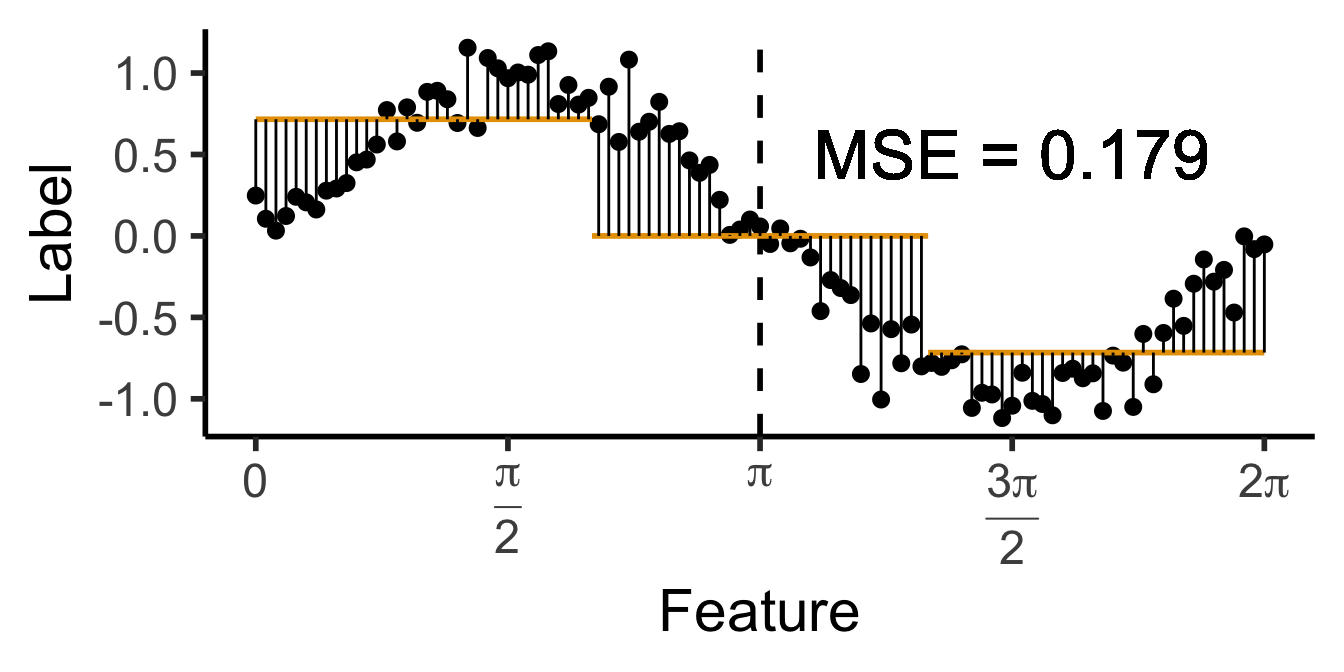
\[ \widehat{y}(x) = \begin{cases} \phantom{-}0.695 &\text{if }x < (1-c)\pi, \\ \phantom{-}0 &\text{if }(1-c)\pi \leq x \leq (1+c)\pi \\ -0.695 &\text{otherwise,} \end{cases} \]
with \(c \approx 0.113\), gives us:
c <- 0.113
cut1 <- (1 - c) * pi
cut2 <- (1 + c) * pi
pos_mean <- 0.695
get_y_pred <- function(x) ifelse(x < cut1, pos_mean, ifelse(x < cut2, 0, -pos_mean))
data_df <- data_df |> mutate(
pred_sq_err1b = (y - get_y_pred(x))^2
)
mse1b <- mean(data_df$pred_sq_err1b)
mse1b_str <- sprintf("%.3f", mse1b)
decision_df <- tribble(
~x, ~xend, ~y, ~yend,
0, cut1, pos_mean, pos_mean,
cut1, cut2, 0, 0,
cut2, 2*pi, -pos_mean, -pos_mean
)
reg_tree_plot +
geom_segment(
data=decision_df,
aes(x=x, xend=xend, y=y, yend=yend),
color=cbPalette[1],
linewidth = g_linewidth
) +
geom_segment(
aes(x=x, xend=x, y=get_y_pred(x), yend=y)
) +
geom_text(
aes(x=(3/2)*pi, y=0.5, label=paste0("MSE = ",mse1b_str)),
size = 9,
#box.padding = unit(c(2,2,2,2), "pt")
)Warning in geom_text(aes(x = (3/2) * pi, y = 0.5, label = paste0("MSE = ", : All aesthetics have length 1, but the data has 101 rows.
ℹ Please consider using `annotate()` or provide this layer with data containing
a single row.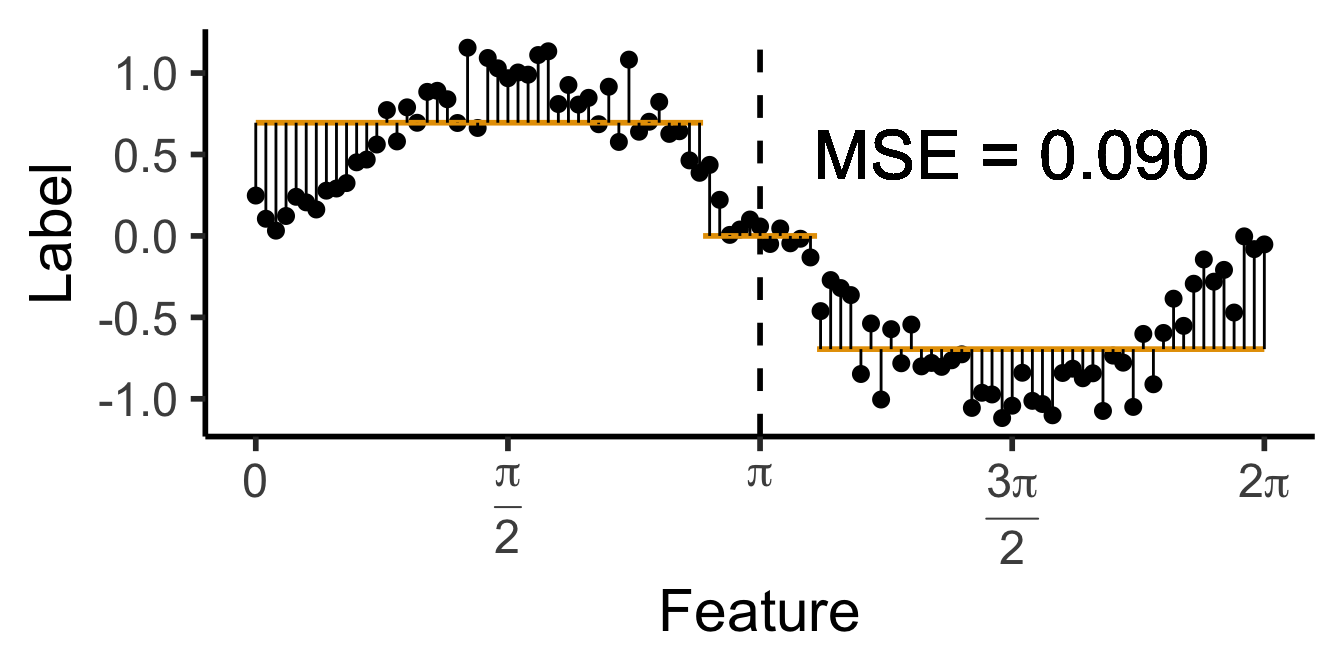
DecisionTreeClassifier and DecisionTreeRegressor classes!Last week we started with classification task (of good vs. bad skiing weather), to get a feel for how decision trees approach these tasks
This week, for a deeper dive into the math/code, let’s start with regression. But why?
\[ \mathscr{L}_{\text{MSE}}\left(\widehat{f}~\right) = \sum_{i=1}^N \left(\widehat{f}(X_i) - \ell_i\right)^2 \]
Once we’re comfortable with how to approach this regression task, we’ll move back to the classification task, where there is no longer a single “obvious” choice for the loss function \(\mathscr{L}\left(\widehat{f}~\right)\)
library(ggtext)
# x_lt_pi = data_df |> filter(x < pi)
# mean(x_lt_pi$y)
data_df <- data_df |> mutate(
pred_sq_err0 = (y - 0)^2
)
mse0 <- mean(data_df$pred_sq_err0)
mse0_str <- sprintf("%.3f", mse0)
reg_tree_plot +
geom_hline(
yintercept = 0,
color=cbPalette[1],
linewidth = g_linewidth
) +
geom_segment(
aes(x=x, xend=x, y=0, yend=y)
) +
geom_text(
aes(x=(3/2)*pi, y=0.5, label=paste0("MSE = ",mse0_str)),
size = 10,
#box.padding = unit(c(2,2,2,2), "pt")
)Warning in geom_text(aes(x = (3/2) * pi, y = 0.5, label = paste0("MSE = ", : All aesthetics have length 1, but the data has 101 rows.
ℹ Please consider using `annotate()` or provide this layer with data containing
a single row.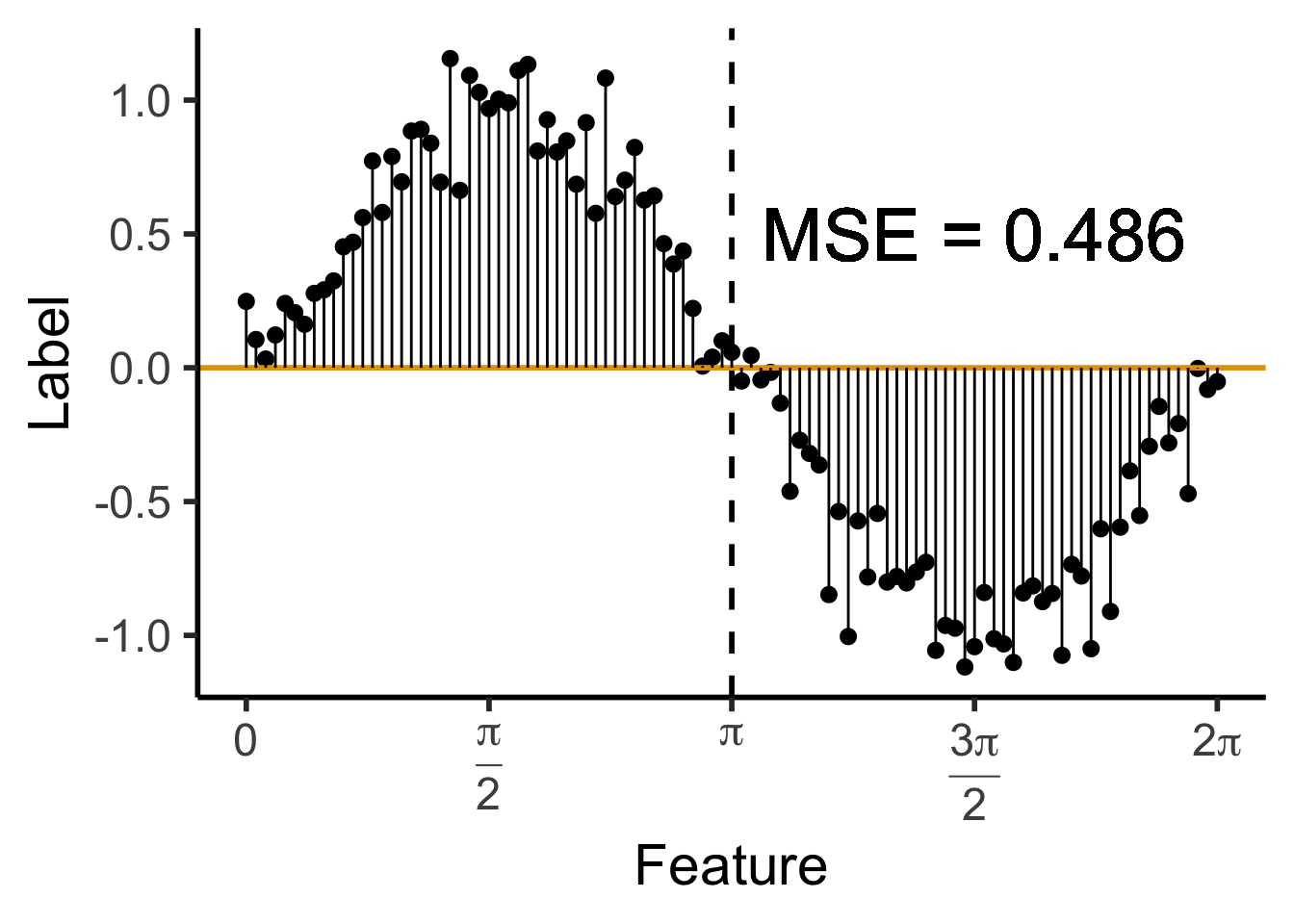
\[ \widehat{y}(x) = \begin{cases} \phantom{-}\frac{2}{\pi} &\text{if }x < \pi, \\ -\frac{2}{\pi} &\text{otherwise.} \end{cases} \]
get_y_pred <- function(x) ifelse(x < pi, 2/pi, -2/pi)
data_df <- data_df |> mutate(
pred_sq_err1 = (y - get_y_pred(x))^2
)
mse1 <- mean(data_df$pred_sq_err1)
mse1_str <- sprintf("%.3f", mse1)
decision_df <- tribble(
~x, ~xend, ~y, ~yend,
0, pi, 2/pi, 2/pi,
pi, 2*pi, -2/pi, -2/pi
)
reg_tree_plot +
geom_segment(
data=decision_df,
aes(x=x, xend=xend, y=y, yend=yend),
color=cbPalette[1],
linewidth = g_linewidth
) +
geom_segment(
aes(x=x, xend=x, y=get_y_pred(x), yend=y)
) +
geom_text(
aes(x=(3/2)*pi, y=0.5, label=paste0("MSE = ",mse1_str)),
size = 9,
#box.padding = unit(c(2,2,2,2), "pt")
)Warning in geom_text(aes(x = (3/2) * pi, y = 0.5, label = paste0("MSE = ", : All aesthetics have length 1, but the data has 101 rows.
ℹ Please consider using `annotate()` or provide this layer with data containing
a single row.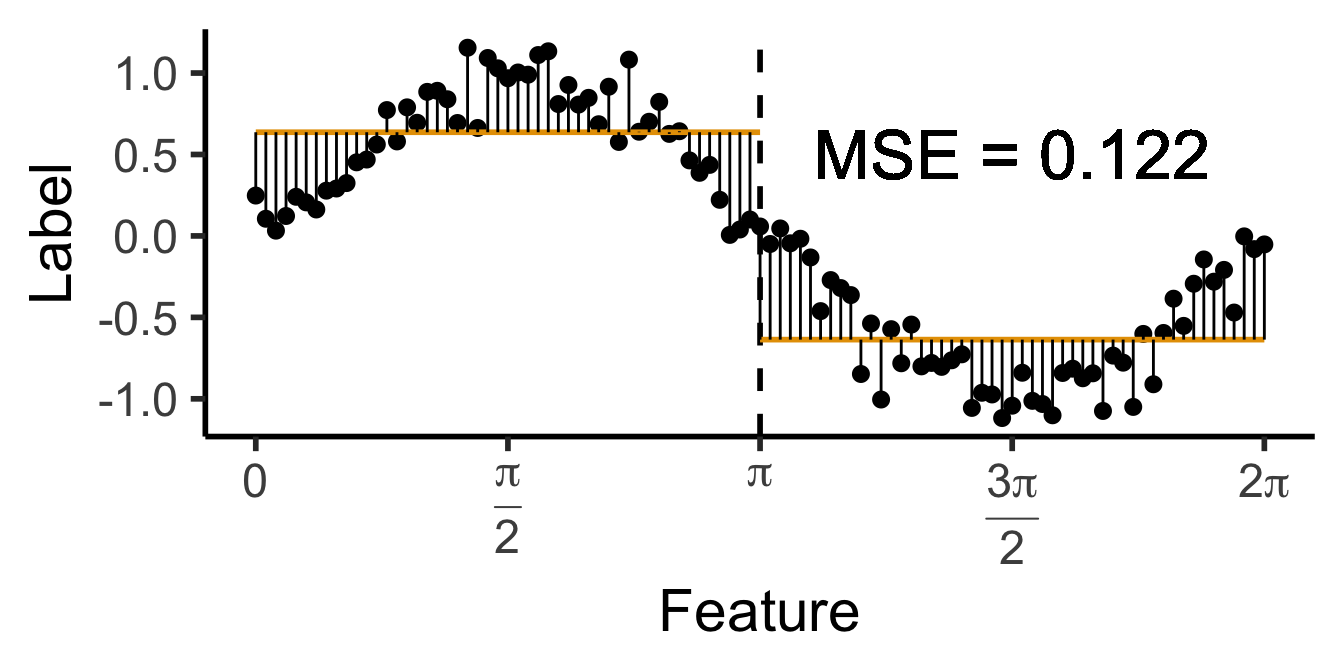
\[ \widehat{y}(x) = \begin{cases} \phantom{-}\frac{9}{4\pi} &\text{if }x < \frac{2\pi}{3}, \\ \phantom{-}0 &\text{if }\frac{2\pi}{3} \leq x \leq \frac{4\pi}{3} \\ -\frac{9}{4\pi} &\text{otherwise.} \end{cases} \]
cut1 <- (2/3) * pi
cut2 <- (4/3) * pi
pos_mean <- 9 / (4*pi)
get_y_pred <- function(x) ifelse(x < cut1, pos_mean, ifelse(x < cut2, 0, -pos_mean))
data_df <- data_df |> mutate(
pred_sq_err1b = (y - get_y_pred(x))^2
)
mse1b <- mean(data_df$pred_sq_err1b)
mse1b_str <- sprintf("%.3f", mse1b)
decision_df <- tribble(
~x, ~xend, ~y, ~yend,
0, (2/3)*pi, pos_mean, pos_mean,
(2/3)*pi, (4/3)*pi, 0, 0,
(4/3)*pi, 2*pi, -pos_mean, -pos_mean
)
reg_tree_plot +
geom_segment(
data=decision_df,
aes(x=x, xend=xend, y=y, yend=yend),
color=cbPalette[1],
linewidth = g_linewidth
) +
geom_segment(
aes(x=x, xend=x, y=get_y_pred(x), yend=y)
) +
geom_text(
aes(x=(3/2)*pi, y=0.5, label=paste0("MSE = ",mse1b_str)),
size = 9,
#box.padding = unit(c(2,2,2,2), "pt")
)Warning in geom_text(aes(x = (3/2) * pi, y = 0.5, label = paste0("MSE = ", : All aesthetics have length 1, but the data has 101 rows.
ℹ Please consider using `annotate()` or provide this layer with data containing
a single row.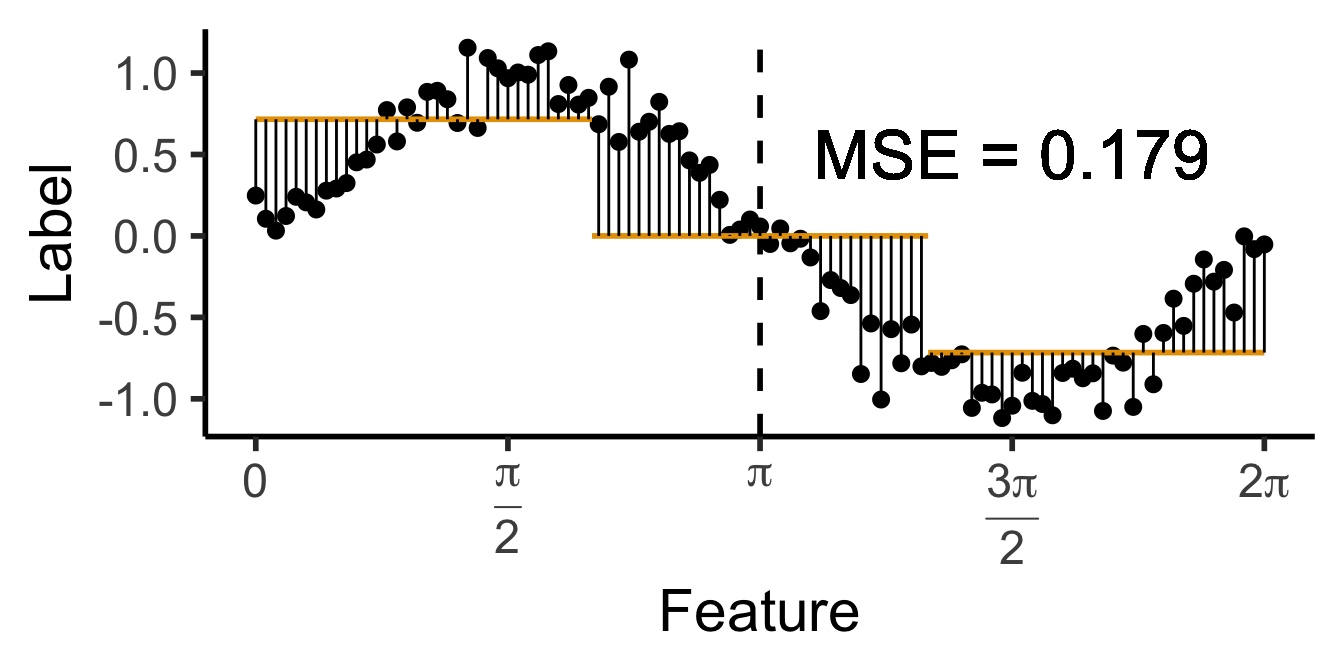
\[ \widehat{y}(x) = \begin{cases} \phantom{-}0.695 &\text{if }x < (1-c)\pi, \\ \phantom{-}0 &\text{if }(1-c)\pi \leq x \leq (1+c)\pi \\ -0.695 &\text{otherwise,} \end{cases} \]
with \(c \approx 0.113\), gives us:
c <- 0.113
cut1 <- (1 - c) * pi
cut2 <- (1 + c) * pi
pos_mean <- 0.695
get_y_pred <- function(x) ifelse(x < cut1, pos_mean, ifelse(x < cut2, 0, -pos_mean))
data_df <- data_df |> mutate(
pred_sq_err1b = (y - get_y_pred(x))^2
)
mse1b <- mean(data_df$pred_sq_err1b)
mse1b_str <- sprintf("%.3f", mse1b)
decision_df <- tribble(
~x, ~xend, ~y, ~yend,
0, cut1, pos_mean, pos_mean,
cut1, cut2, 0, 0,
cut2, 2*pi, -pos_mean, -pos_mean
)
reg_tree_plot +
geom_segment(
data=decision_df,
aes(x=x, xend=xend, y=y, yend=yend),
color=cbPalette[1],
linewidth = g_linewidth
) +
geom_segment(
aes(x=x, xend=x, y=get_y_pred(x), yend=y)
) +
geom_text(
aes(x=(3/2)*pi, y=0.5, label=paste0("MSE = ",mse1b_str)),
size = 9,
#box.padding = unit(c(2,2,2,2), "pt")
)Warning in geom_text(aes(x = (3/2) * pi, y = 0.5, label = paste0("MSE = ", : All aesthetics have length 1, but the data has 101 rows.
ℹ Please consider using `annotate()` or provide this layer with data containing
a single row.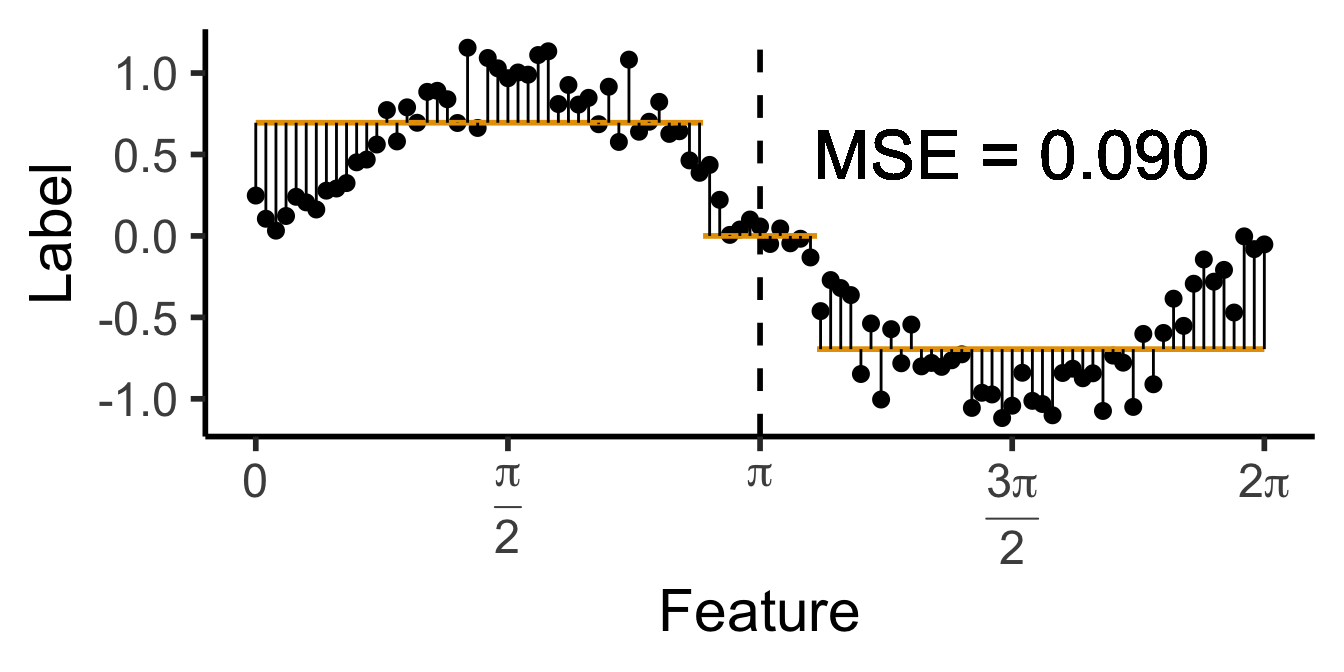
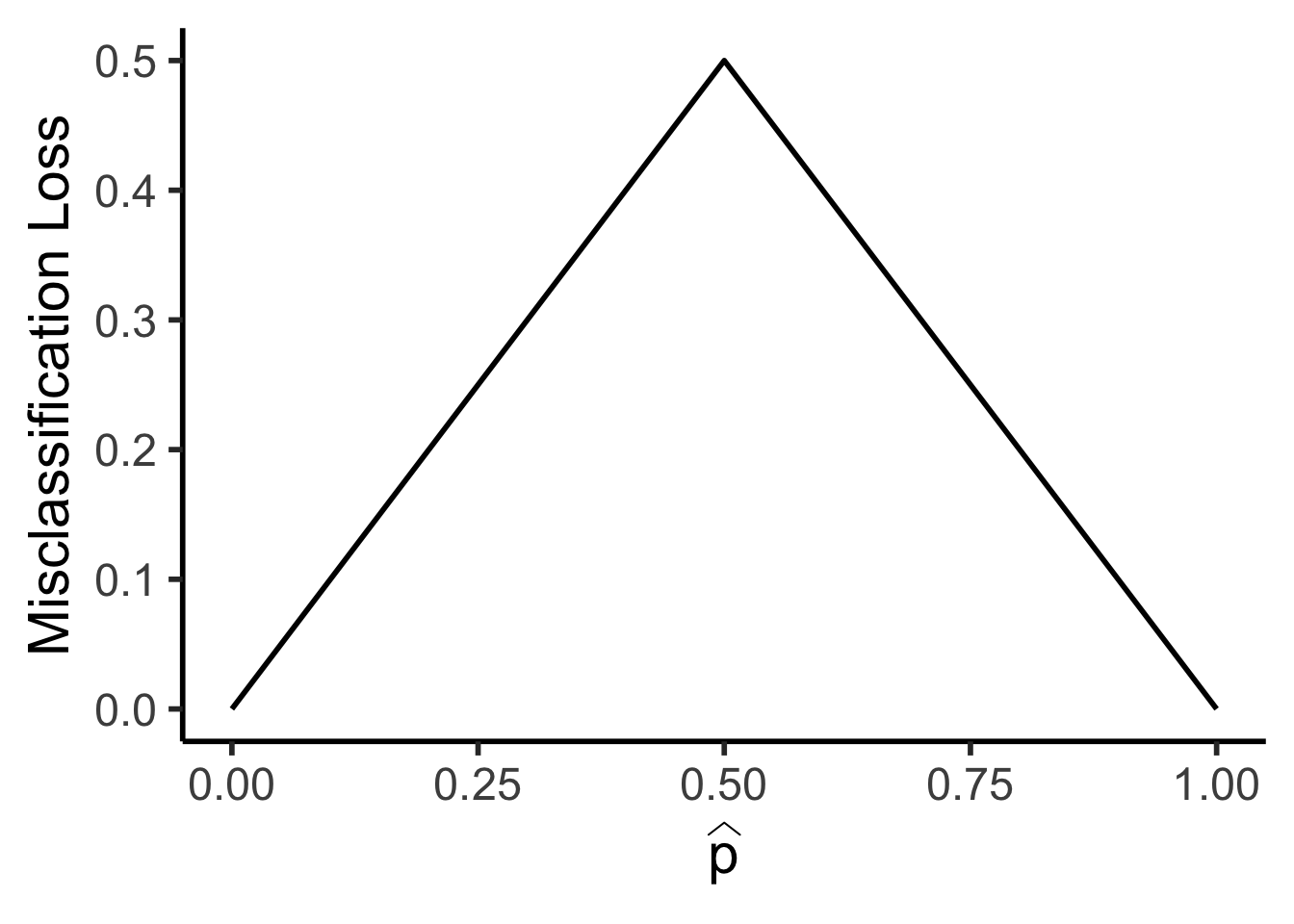
\[ \mathscr{L}_{MC}(R) = 1 - \widehat{p}_{R} \]
library(tidyverse)
library(latex2exp)
my_mc <- function(p) 0.5 - abs(0.5 - p)
x_vals <- seq(0, 1, 0.01)
mc_vals <- sapply(x_vals, my_mc)
phat_label <- TeX('$\\widehat{p}$')
data_df <- tibble(x=x_vals, loss_mc=mc_vals)
ggplot(data_df, aes(x=x, y=loss_mc)) +
geom_line(linewidth = g_linewidth) +
dsan_theme("half") +
labs(
x = phat_label,
y = "Misclassification Loss"
)
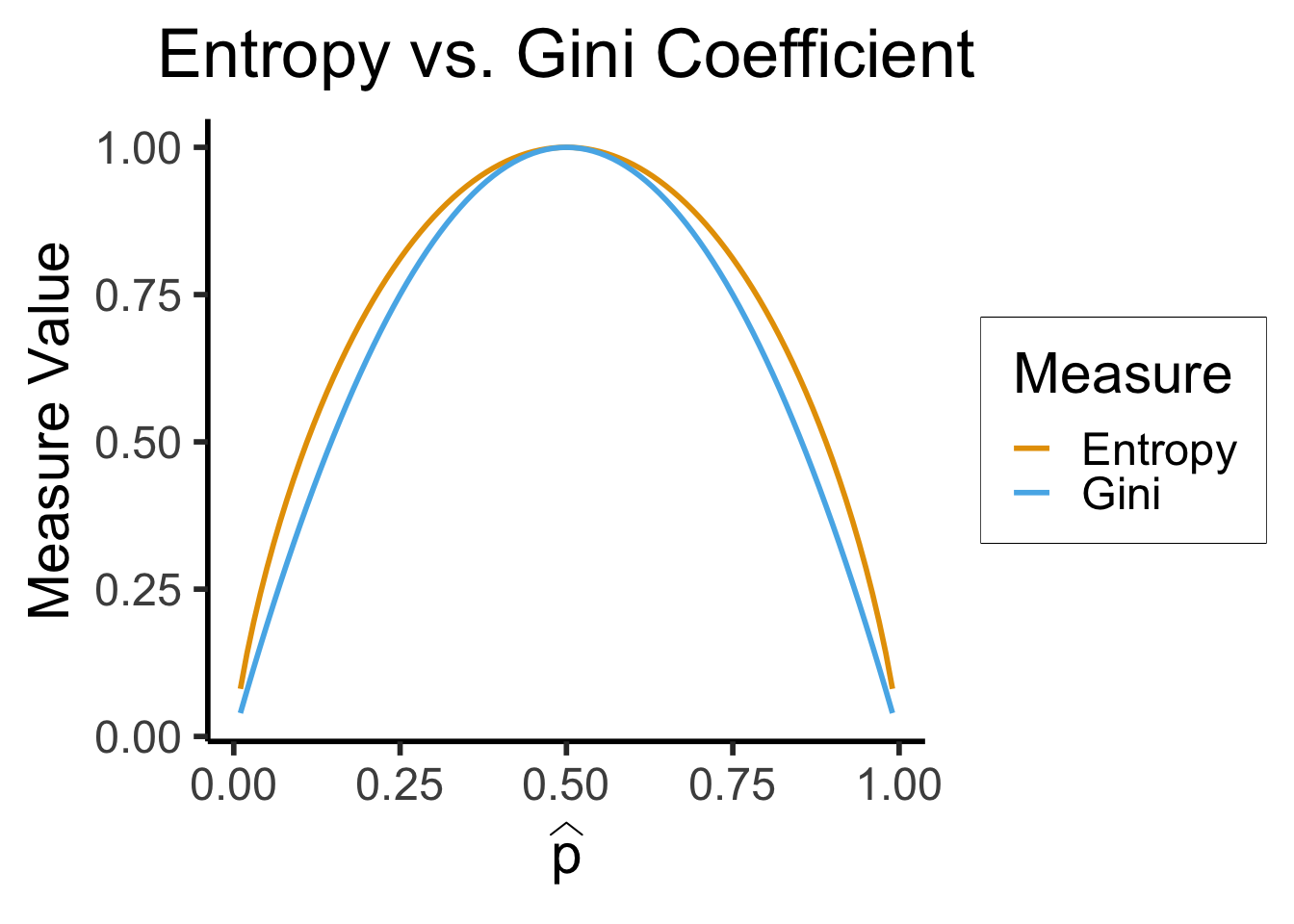
\[ \mathscr{L}_{\text{Ent}}(\widehat{p}) = -\sum_{i=1}^K \widehat{p}_k\log_2(\widehat{p}_k) \]
\[ \mathscr{L}_{\text{Gini}}(\widehat{p}) = -\sum_{i=1}^K \widehat{p}_k(1-\widehat{p}_k) \]
library(tidyverse)
library(latex2exp)
phat_label <- TeX('$\\widehat{p}')
my_ent <- function(p) -(p*log2(p) + (1-p)*log2(1-p))
my_gini <- function(p) 4*p*(1-p)
x_vals <- seq(0.01, 0.99, 0.01)
ent_vals <- sapply(x_vals, my_ent)
ent_df <- tibble(x=x_vals, y=ent_vals, Measure="Entropy")
gini_vals <- sapply(x_vals, my_gini)
gini_df <- tibble(x=x_vals, y=gini_vals, Measure="Gini")
data_df <- bind_rows(ent_df, gini_df)
ggplot(data=data_df, aes(x=x, y=y, color=Measure)) +
geom_line(linewidth = g_linewidth) +
dsan_theme("half") +
scale_color_manual(values=c(cbPalette[1], cbPalette[2])) +
labs(
x = phat_label,
y = "Measure Value",
title = "Entropy vs. Gini Coefficient"
)
\[ (j^*, s^*) = \argmax_{j, s}\left[ \mathscr{L}(R_1(j,s)) + \mathscr{L}(R_2(j,s)) \right], \]
where
\[ R_1(j, s) = \{X \mid X_j < s\}, \; R_2(j, s) = \{X \mid X_j \geq s\}. \]
library(tidyverse)
library(lubridate)
set.seed(5001)
sample_size <- 100
day <- seq(ymd('2023-01-01'),ymd('2023-12-31'),by='weeks')
lat_bw <- 5
latitude <- seq(-90, 90, by=lat_bw)
ski_df <- expand_grid(day, latitude)
ski_df <- tibble::rowid_to_column(ski_df, var='obs_id')
#ski_df |> head()
# Data-generating process
lat_cutoff <- 35
ski_df <- ski_df |> mutate(
near_equator = abs(latitude) <= lat_cutoff,
northern = latitude > lat_cutoff,
southern = latitude < -lat_cutoff,
first_3m = day < ymd('2023-04-01'),
last_3m = day >= ymd('2023-10-01'),
middle_6m = (day >= ymd('2023-04-01')) & (day < ymd('2023-10-01')),
snowfall = 0
)
# Update the non-zero sections
mu_snow <- 10
sd_snow <- 2.5
# How many northern + first 3 months
num_north_first_3 <- nrow(ski_df[ski_df$northern & ski_df$first_3m,])
ski_df[ski_df$northern & ski_df$first_3m, 'snowfall'] = rnorm(num_north_first_3, mu_snow, sd_snow)
# Northerns + last 3 months
num_north_last_3 <- nrow(ski_df[ski_df$northern & ski_df$last_3m,])
ski_df[ski_df$northern & ski_df$last_3m, 'snowfall'] = rnorm(num_north_last_3, mu_snow, sd_snow)
# How many southern + middle 6 months
num_south_mid_6 <- nrow(ski_df[ski_df$southern & ski_df$middle_6m,])
ski_df[ski_df$southern & ski_df$middle_6m, 'snowfall'] = rnorm(num_south_mid_6, mu_snow, sd_snow)
# And collapse into binary var
ski_df['good_skiing'] = ski_df$snowfall > 0
# This converts day into an int
ski_df <- ski_df |> mutate(
day_num = lubridate::yday(day)
)
#print(nrow(ski_df))
ski_sample <- ski_df |> slice_sample(n = sample_size)
ski_sample |> write_csv("assets/ski.csv")
month_vec <- c(ymd('2023-01-01'), ymd('2023-02-01'), ymd('2023-03-01'), ymd('2023-04-01'), ymd('2023-05-01'), ymd('2023-06-01'), ymd('2023-07-01'), ymd('2023-08-01'), ymd('2023-09-01'), ymd('2023-10-01'), ymd('2023-11-01'), ymd('2023-12-01'))
month_labels <- c("Jan", "Feb", "Mar", "Apr", "May", "Jun", "Jul", "Aug", "Sep", "Oct", "Nov", "Dec")
lat_vec <- c(-90, -60, -30, 0, 30, 60, 90)
ggplot(
ski_sample,
aes(
x=day,
y=latitude,
#shape=good_skiing,
color=good_skiing
)) +
geom_point(
size = g_pointsize / 1.5,
#stroke=1.5
) +
dsan_theme() +
labs(
x = "Time of Year",
y = "Latitude",
shape = "Good Skiing?"
) +
scale_shape_manual(name="Good Skiing?", values=c(1, 3)) +
scale_color_manual(name="Good Skiing?", values=c(cbPalette[1], cbPalette[2]), labels=c("No (Sunny)","Yes (Snowy)")) +
scale_x_continuous(
breaks=c(month_vec,ymd('2024-01-01')),
labels=c(month_labels,"Jan")
) +
scale_y_continuous(breaks=lat_vec)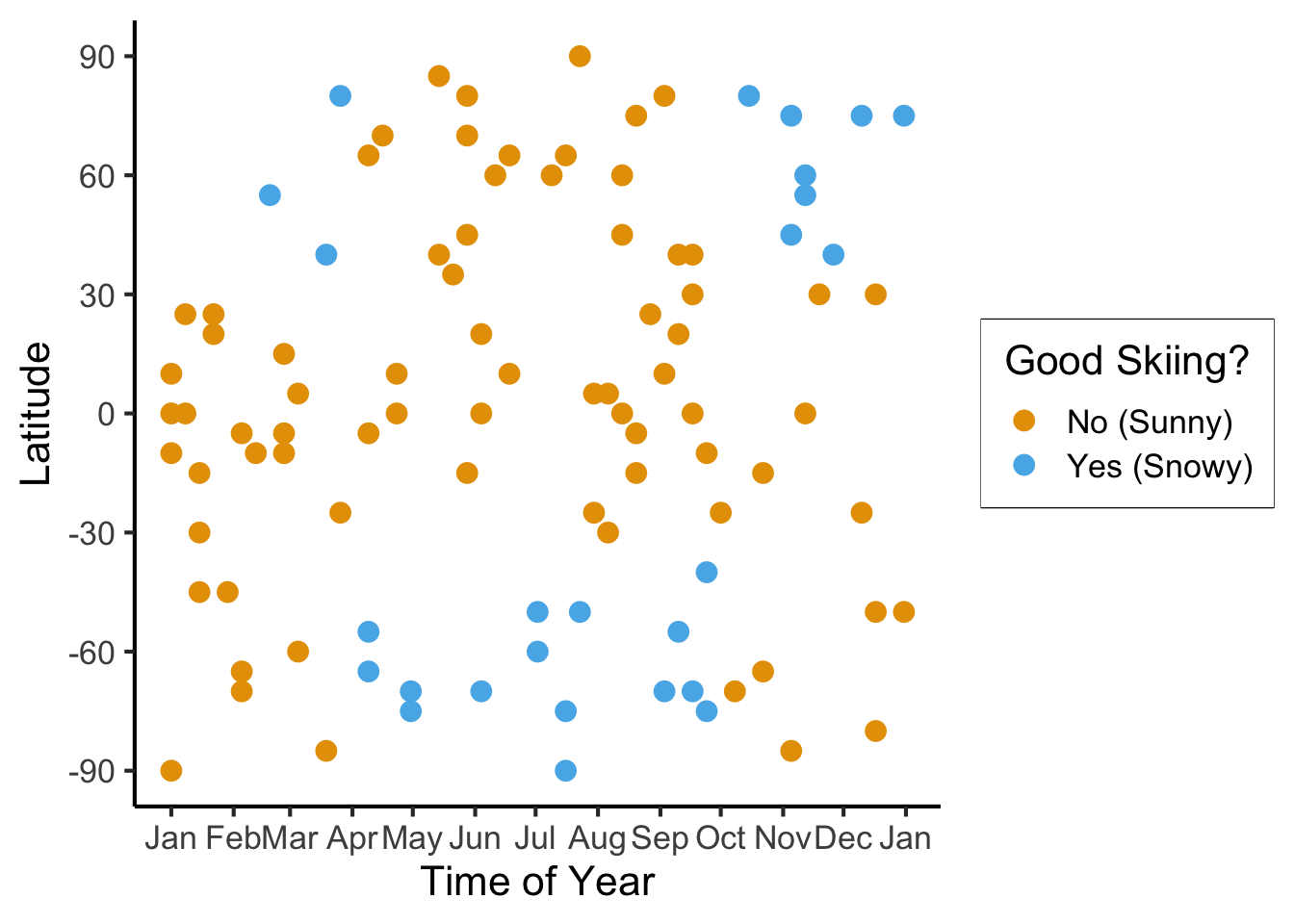
ski_sample |> count(good_skiing)| good_skiing | n |
|---|---|
| FALSE | 74 |
| TRUE | 26 |
\[ \mathscr{L}(R_i) = -[(0.74)\log_2(0.74) + (0.26)\log_2(0.26)] \approx 0.8267 \]
Given that \(\mathscr{L}(R_P) \approx 0.9427\), let’s think through two choices for the first split:
ski_sample <- ski_sample |> mutate(
lat_lt_n425 = latitude < -42.5
)
r1a <- ski_sample |> filter(lat_lt_n425) |> summarize(
good_skiing = sum(good_skiing),
total = n()
) |> mutate(region = "R1(A)", .before=good_skiing)
r2a <- ski_sample |> filter(lat_lt_n425 == FALSE) |> summarize(
good_skiing = sum(good_skiing),
total = n()
) |> mutate(region = "R2(A)", .before=good_skiing)
choice_a_df <- bind_rows(r1a, r2a)
choice_a_df
ski_sample <- ski_sample |> mutate(
month_lt_oct = day < ymd('2023-10-01')
)
r1b <- ski_sample |> filter(month_lt_oct) |> summarize(
good_skiing = sum(good_skiing),
total = n()
) |> mutate(region = "R1(B)", .before=good_skiing)
r2b <- ski_sample |> filter(month_lt_oct == FALSE) |> summarize(
good_skiing = sum(good_skiing),
total = n()
) |> mutate(region = "R2(B)", .before=good_skiing)
choice_b_df <- bind_rows(r1b, r2b)
choice_b_df\[ \begin{align*} R_1^A &= \{X_i \mid X_{i,\text{lat}} < -42.5\} \\ R_2^A &= \{X_i \mid X_{i,\text{lat}} \geq -42.5\} \end{align*} \]
| region | good_skiing | total |
|---|---|---|
| R1(A) | 14 | 27 |
| R2(A) | 12 | 73 |
\[ \begin{align*} \mathscr{L}(R_1^A) &= -\mkern-4mu\left[ \frac{21}{32}\log_2\frac{21}{32} + \frac{11}{32}\log_2\frac{11}{32} \right] \approx 0.9284 \\ \mathscr{L}(R_2^A) &= -\mkern-4mu\left[ \frac{15}{68}\log_2\frac{15}{68} + \frac{53}{68}\log_2\frac{53}{68}\right] \approx 0.7612 \\ \implies \mathscr{L}(A) &= \frac{32}{100}(0.9284) + \frac{68}{100}(0.7612) \approx 0.8147 % < 0.9427 \end{align*} \]
\[ \begin{align*} R_1^B &= \{X_i \mid X_{i,\text{month}} < \text{October}\} \\ R_2^B &= \{X_i \mid X_{i,\text{month}} \geq \text{October}\} \end{align*} \]
| region | good_skiing | total |
|---|---|---|
| R1(B) | 18 | 80 |
| R2(B) | 8 | 20 |
\[ \begin{align*} \mathscr{L}(R_1^B) &= -\mkern-4mu\left[ \frac{28}{75}\log_2\frac{28}{75} + \frac{47}{75}\log_2\frac{47}{75}\right] \approx 0.9532 \\ \mathscr{L}(R_2^B) &= -\mkern-4mu\left[ \frac{8}{25}\log_2\frac{8}{25} + \frac{17}{25}\log_2\frac{17}{25} \right] \approx 0.9044 \\ \implies \mathscr{L}(B) &= \frac{75}{100}(0.9532) + \frac{25}{100}(0.9044) \approx 0.941 \end{align*} \]
max_levels, or min_samples_leaf)| Player | Skill |
|---|---|
| Larry “Lefty” Lechuga | Always hits 5cm left of bullseye |
| Rico Righty | Always hits 5cm right of bullseye |
| Lil Uppy Vert | Always hits 5cm above bullseye |
| Inconsistent Inkyung | Hits bullseye 50% of time, other 50% hits random point |
| Diagonal Dave | Always hits 5cm above right of bullseye |
| Dobert Downy Jr. | Always hits 5cm below bullseye |
| Gregor “the GOAT” Gregorsson | Hits bullseye 99.9% of time, other 0.1% hits random point |
| Craig | Top 25 Craigs of 2023 |

 , and the effect goes away (biases no longer cancel out)
, and the effect goes away (biases no longer cancel out)library(ggtext)
# x_lt_pi = data_df |> filter(x < pi)
# mean(x_lt_pi$y)
data_df <- data_df |> mutate(
pred_sq_err0 = (y - 0)^2
)
mse0 <- mean(data_df$pred_sq_err0)
mse0_str <- sprintf("%.3f", mse0)
reg_tree_plot +
geom_hline(
yintercept = 0,
color=cbPalette[1],
linewidth = g_linewidth
) +
geom_segment(
aes(x=x, xend=x, y=0, yend=y)
) +
geom_text(
aes(x=(3/2)*pi, y=0.5, label=paste0("MSE = ",mse0_str)),
size = 10,
#box.padding = unit(c(2,2,2,2), "pt")
)
get_y_pred <- function(x) ifelse(x < pi, 2/pi, -2/pi)
data_df <- data_df |> mutate(
pred_sq_err1 = (y - get_y_pred(x))^2
)
mse1 <- mean(data_df$pred_sq_err1)
mse1_str <- sprintf("%.3f", mse1)
decision_df <- tribble(
~x, ~xend, ~y, ~yend,
0, pi, 2/pi, 2/pi,
pi, 2*pi, -2/pi, -2/pi
)
reg_tree_plot +
geom_segment(
data=decision_df,
aes(x=x, xend=xend, y=y, yend=yend),
color=cbPalette[1],
linewidth = g_linewidth
) +
geom_segment(
aes(x=x, xend=x, y=get_y_pred(x), yend=y)
) +
geom_text(
aes(x=(3/2)*pi, y=0.5, label=paste0("MSE = ",mse1_str)),
size = 9,
#box.padding = unit(c(2,2,2,2), "pt")
)Warning in geom_text(aes(x = (3/2) * pi, y = 0.5, label = paste0("MSE = ", : All aesthetics have length 1, but the data has 101 rows.
ℹ Please consider using `annotate()` or provide this layer with data containing
a single row.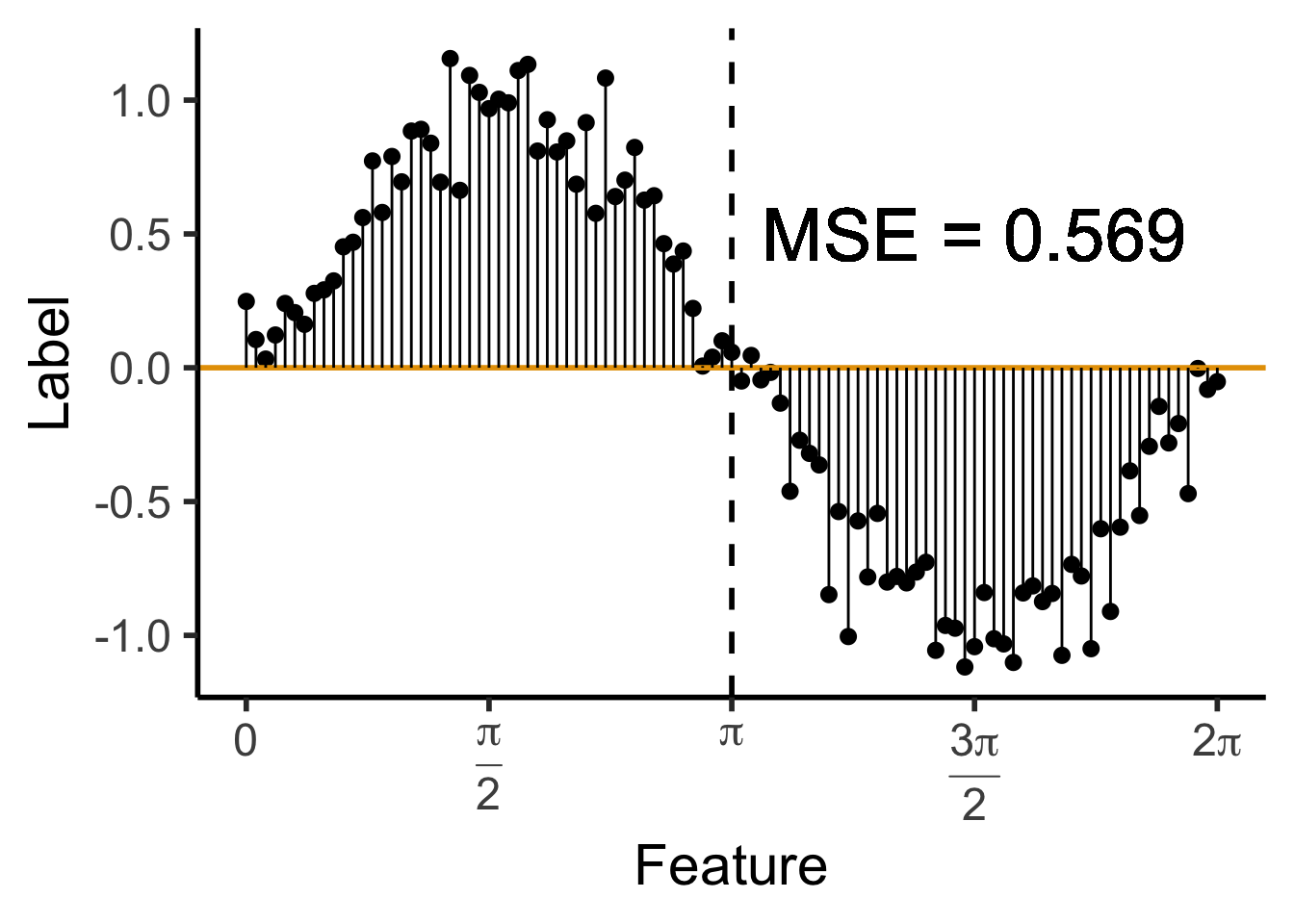
Warning in geom_text(aes(x = (3/2) * pi, y = 0.5, label = paste0("MSE = ", : All aesthetics have length 1, but the data has 101 rows.
ℹ Please consider using `annotate()` or provide this layer with data containing
a single row.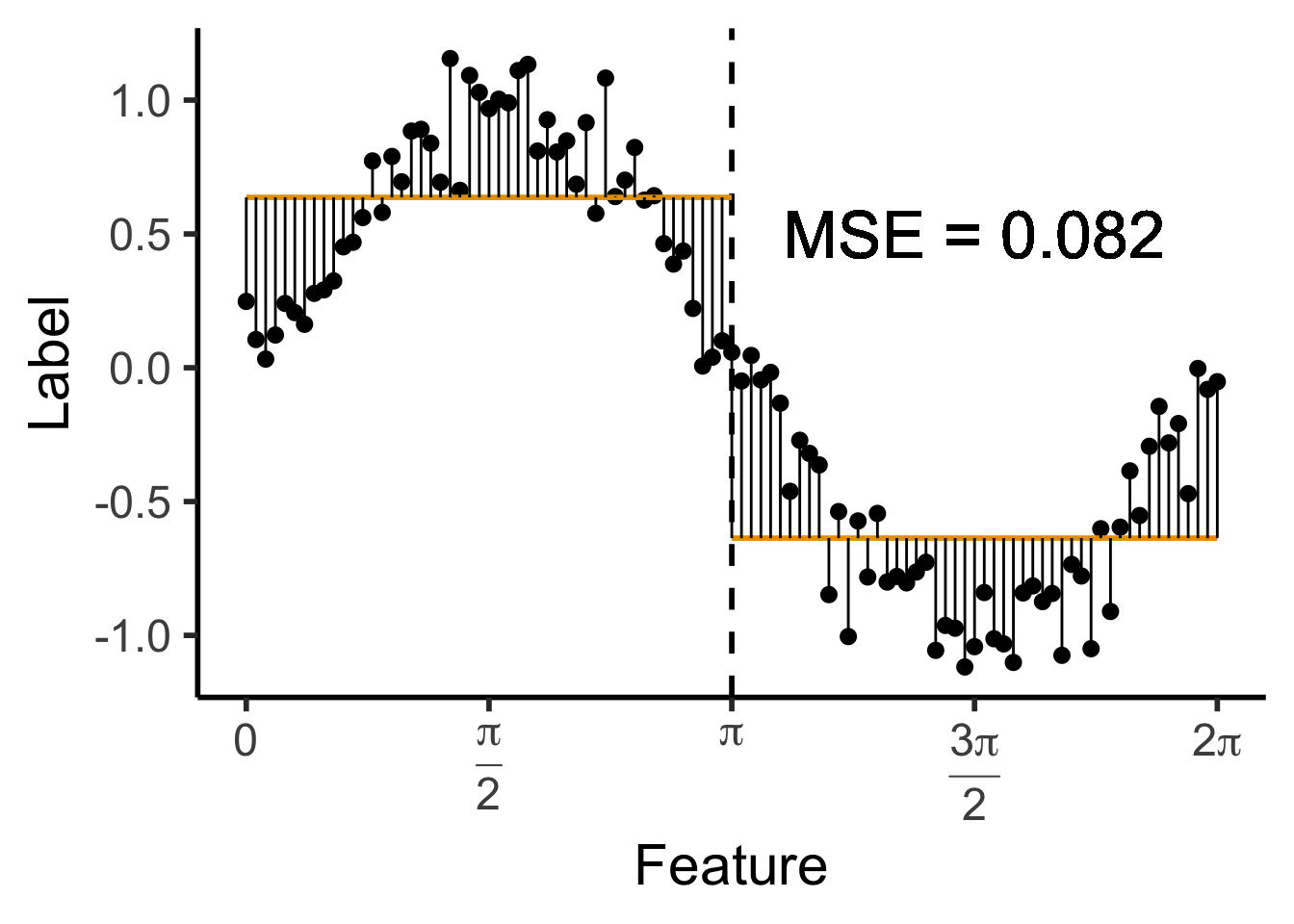
\[ \mathbf{\Sigma}' = \mathbf{V}\mathbf{\Sigma}\mathbf{V}^{-1}. \]