Week 11: Random Forests
DSAN 5000: Data Science and Analytics
Thursday, November 14, 2024
Decision Trees
\[ \DeclareMathOperator*{\argmax}{argmax} \DeclareMathOperator*{\argmin}{argmin} \newcommand{\bigexp}[1]{\exp\mkern-4mu\left[ #1 \right]} \newcommand{\bigexpect}[1]{\mathbb{E}\mkern-4mu \left[ #1 \right]} \newcommand{\definedas}{\overset{\text{defn}}{=}} \newcommand{\definedalign}{\overset{\phantom{\text{defn}}}{=}} \newcommand{\eqeventual}{\overset{\text{eventually}}{=}} \newcommand{\expect}[1]{\mathbb{E}[#1]} \newcommand{\expectsq}[1]{\mathbb{E}^2[#1]} \newcommand{\fw}[1]{\texttt{#1}} \newcommand{\given}{\mid} \newcommand{\green}[1]{\color{green}{#1}} \newcommand{\heads}{\outcome{heads}} \newcommand{\lik}{\mathcal{L}} \newcommand{\mle}{\textsf{ML}} \newcommand{\orange}[1]{\color{orange}{#1}} \newcommand{\outcome}[1]{\textsf{#1}} \newcommand{\param}[1]{{\color{purple} #1}} \newcommand{\paramDist}{\param{\boldsymbol\theta_\mathcal{D}}} \newcommand{\pgsamplespace}{\{\green{1},\green{2},\green{3},\purp{4},\purp{5},\purp{6}\}} \newcommand{\prob}[1]{P\left( #1 \right)} \newcommand{\purp}[1]{\color{purple}{#1}} \newcommand{\spacecap}{\; \cap \;} \newcommand{\spacewedge}{\; \wedge \;} \newcommand{\tails}{\outcome{tails}} \newcommand{\Var}[1]{\text{Var}[#1]} \newcommand{\bigVar}[1]{\text{Var}\mkern-4mu \left[ #1 \right]} \]
20 Questions
- I am thinking of some entity. What is it?
- What questions should we ask initially?
- Why might questions on the left be more helpful than questions on the right?
| General Questions | Specific Questions |
|---|---|
| Is it a physical object? | Is it a soda can? |
| Is it an animal? | Is it a cat? |
| Is it bigger than a house? | Is it a planet? |
We Can Quantify How Good a Sequence of Questions Is!
- Assume we’re playing with someone who only knows three objects \(S = \{\text{Tree}, \text{Bird}, \text{Car}\}\), and they randomize among these such that
| \(\text{Choice}\) | Tree | Bird | Car |
| \(\Pr(\text{Choice})\) | 0.25 | 0.25 | 0.50 |
- Why might the “script” on the left be a better choice than script in the middle? Why are left and middle both better than right?
Let’s Use Math
- An optimal script minimizes average number of questions required to reach answer
\[ \begin{align*} &\mathbb{E}[\text{\# Moves}] \\ =\,&1 \cdot \Pr(\text{Car}) + 2 \cdot \Pr(\text{Bird}) \\ &+ 2 \cdot \Pr(\text{Tree}) \\ =\,&1 \cdot 0.5 + 2\cdot 0.25 + 2\cdot 0.25 \\ =\,&1.5 \end{align*} \]
\[ \begin{align*} &\mathbb{E}[\text{\# Moves}] \\ =\,&1 \cdot \Pr(\text{Bird}) + 2 \cdot \Pr(\text{Car}) \\ &+ 2 \cdot \Pr(\text{Tree}) \\ =\,&1 \cdot 0.25 + 2\cdot 0.5 + 2\cdot 0.25 \\ =\,&1.75 \end{align*} \]
\[ \begin{align*} &\mathbb{E}[\text{\# Moves}] \\ =\,&1 \cdot \Pr(\text{Bird}) + 3 \cdot \Pr(\text{Car}) \\ &+ 3 \cdot \Pr(\text{Tree}) \\ =\,&1 \cdot 0.25 + 3\cdot 0.5 + 3\cdot 0.25 \\ =\,&2.5 \end{align*} \]
Let’s Use (Different) Math
- Forgetting about the individual trees for a moment, let’s compute the entropy of the RV representing the opponent’s choice.
- In general, if \(X\) represents the opponent’s choice and \(\mathcal{R}_X = \{1, 2, \ldots, N\}\), the entropy of \(X\) is:
\[ \begin{align*} H(X) &= -\sum_{i=1}^N \Pr(X = i)\log_2\Pr(X = i) \end{align*} \]
- So in our case we have:
\[ \begin{align*} H(X) &= -\left[ \Pr(X = \text{Car}) \log_2\Pr(X = \text{Car}) \right. \\ &\phantom{= -[ } + \Pr(X = \text{Bird})\log_2\Pr(X = \text{Bird}) \\ &\phantom{= -[ } + \left. \Pr(X = \text{Tree})\log_2\Pr(X = \text{Tree})\right] \\ &= -\left[ (0.5)(-1) + (0.25)(-2) + (0.25)(-2) \right] = 1.5~🧐 \end{align*} \]
Entropy Seems Helpful Here…
- Now let’s imagine our opponent randomizes between all three options:
\[ \begin{align*} \mathbb{E}[\text{\# Moves}] &= 1 \cdot (1/3) + 2 \cdot (1/3) + 2 \cdot (1/3) \\ &= \frac{5}{3} \approx 1.667 \end{align*} \]
\[ \begin{align*} H(X) &= -\left[ \Pr(X = \text{Car}) \log_2\Pr(X = \text{Car}) \right. \\ &\phantom{= -[ } + \Pr(X = \text{Bird})\log_2\Pr(X = \text{Bird}) \\ &\phantom{= -[ } + \left. \Pr(X = \text{Tree})\log_2\Pr(X = \text{Tree})\right] \\ &= -\left[ \frac{1}{3}\log_2\left(\frac{1}{3}\right) + \frac{1}{3}\log_2\left(\frac{1}{3}\right) + \frac{1}{3}\log_2\left(\frac{1}{3}\right) \right] \approx 1.585~🧐 \end{align*} \]
The Mathematical Relationship
The smallest possible number of levels \(L^*\) for a script based on RV \(X\) is exactly
\[ L^* = \lceil H(X) \rceil \]
Intuition: Although \(\mathbb{E}[\text{\# Moves}] = 1.5\), we cannot have a tree with 1.5 levels!
Entropy provides a lower bound on \(\mathbb{E}[\text{\# Moves}]\):
\[ \mathbb{E}[\text{\# Moves}] \geq H(X) \]
Decision Tree Structure
- Leaf Nodes represent outcomes
- Branch Nodes represent questions
How Are They Built?
- Example: we find ourselves at some point on the globe, at some time during the year, and we’re trying to see whether this point+time are good for skiing
Code
library(tidyverse)
library(lubridate)
set.seed(5001)
sample_size <- 100
day <- seq(ymd('2023-01-01'),ymd('2023-12-31'),by='weeks')
lat_bw <- 5
latitude <- seq(-90, 90, by=lat_bw)
ski_df <- expand_grid(day, latitude)
#ski_df |> head()
# Data-generating process
lat_cutoff <- 35
ski_df <- ski_df |> mutate(
near_equator = abs(latitude) <= lat_cutoff,
northern = latitude > lat_cutoff,
southern = latitude < -lat_cutoff,
first_3m = day < ymd('2023-04-01'),
last_3m = day >= ymd('2023-10-01'),
middle_6m = (day >= ymd('2023-04-01')) & (day < ymd('2023-10-01')),
snowfall = 0
)
# Update the non-zero sections
mu_snow <- 10
sd_snow <- 2.5
# How many northern + first 3 months
num_north_first_3 <- nrow(ski_df[ski_df$northern & ski_df$first_3m,])
ski_df[ski_df$northern & ski_df$first_3m, 'snowfall'] = rnorm(num_north_first_3, mu_snow, sd_snow)
# Northerns + last 3 months
num_north_last_3 <- nrow(ski_df[ski_df$northern & ski_df$last_3m,])
ski_df[ski_df$northern & ski_df$last_3m, 'snowfall'] = rnorm(num_north_last_3, mu_snow, sd_snow)
# How many southern + middle 6 months
num_south_mid_6 <- nrow(ski_df[ski_df$southern & ski_df$middle_6m,])
ski_df[ski_df$southern & ski_df$middle_6m, 'snowfall'] = rnorm(num_south_mid_6, mu_snow, sd_snow)
# And collapse into binary var
ski_df['good_skiing'] = ski_df$snowfall > 0
# This converts day into an int
ski_df <- ski_df |> mutate(
day_num = lubridate::yday(day)
)
#print(nrow(ski_df))
ski_sample <- ski_df |> slice_sample(n = sample_size)
ski_sample |> write_csv("assets/ski.csv")
ggplot(
ski_sample,
aes(
x=day,
y=latitude,
#shape=good_skiing,
color=good_skiing
)) +
geom_point(
size = g_pointsize / 1.5,
#stroke=1.5
) +
dsan_theme() +
labs(
x = "Time of Year",
y = "Latitude",
shape = "Good Skiing?"
) +
scale_shape_manual(name="Good Skiing?", values=c(1, 3)) +
scale_color_manual(name="Good Skiing?", values=c(cbPalette[1], cbPalette[2]), labels=c("No (Sunny)","Yes (Snowy)")) +
scale_x_continuous(
breaks=c(ymd('2023-01-01'), ymd('2023-02-01'), ymd('2023-03-01'), ymd('2023-04-01'), ymd('2023-05-01'), ymd('2023-06-01'), ymd('2023-07-01'), ymd('2023-08-01'), ymd('2023-09-01'), ymd('2023-10-01'), ymd('2023-11-01'), ymd('2023-12-01')),
labels=c("Jan", "Feb", "Mar", "Apr", "May", "Jun", "Jul", "Aug", "Sep", "Oct", "Nov", "Dec")
) +
scale_y_continuous(breaks=c(-90, -60, -30, 0, 30, 60, 90))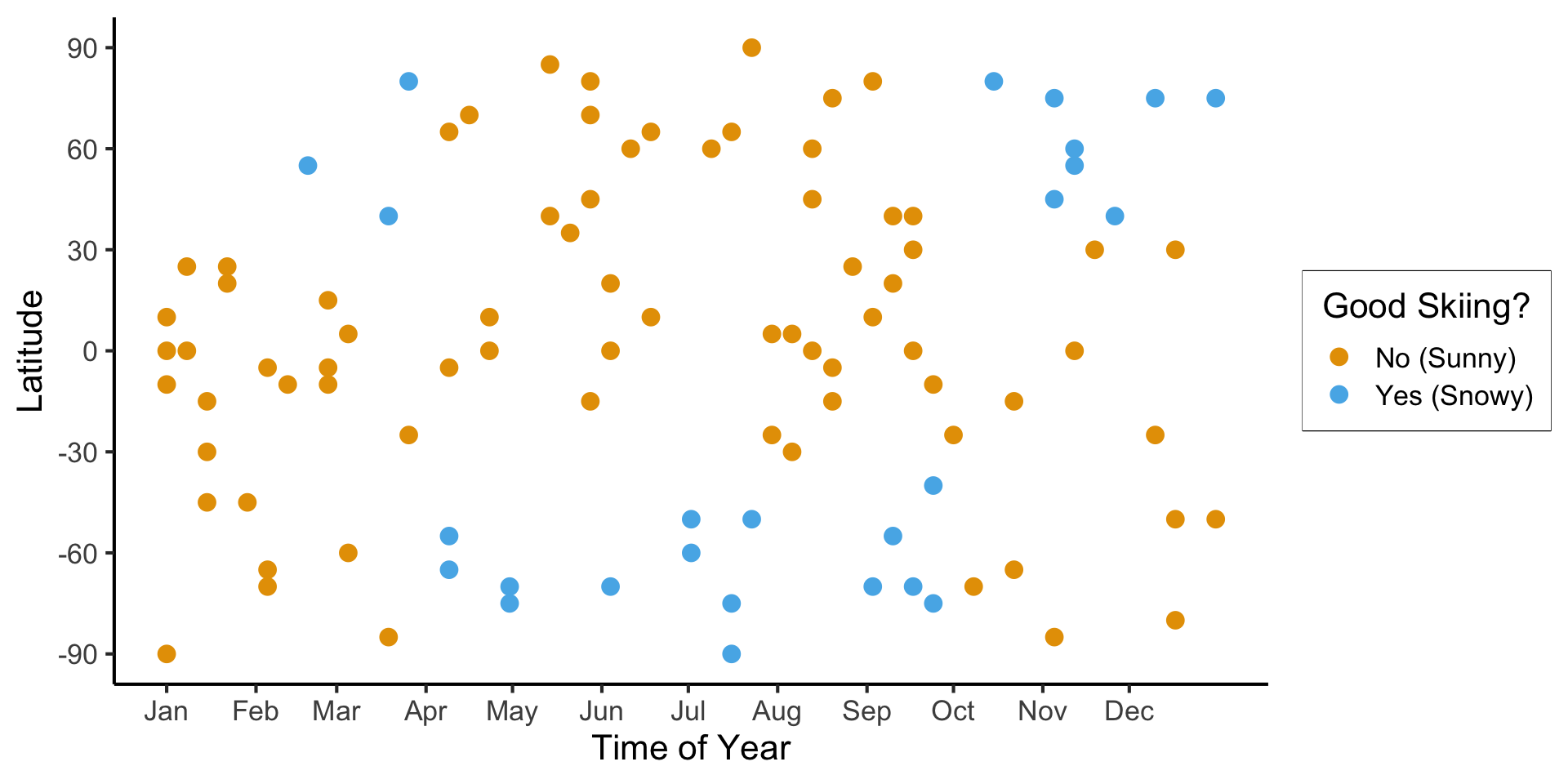
(Example adapted from CS229: Machine Learning, Stanford University)
Zero Splits
- Starting out: no splits at all, just guess most frequent class: bad skiing
- This gives us \(\Pr(\text{Correct Guess}) = 0.74\)
- Let \(R_i\) denote the region we’re considering at level \(i\), and \(\widehat{p}_c(R_i)\) be the proportion of points in region \(R_i\) that are of class \(c\)
- The (nearly) unique measure is, you guessed it: entropy:
\[ \mathscr{L}(R_i) = -\sum_{c}\widehat{p}_c(R_i)\log_2(\widehat{p}_c(R_i)) \]
- Here, since we’re not splitting the region up at all (yet), the entropy is just
\[ \mathscr{L}(R_i) = -[(0.74)\log_2(0.74) + (0.26)\log_2(0.26)] \approx 0.827 \]
Judging Split Options
Let’s think through two choices for the first split:
Code
\(\text{latitude} \leq -47.5\):
| lat_lt_475 | good_skiing | n |
|---|---|---|
| FALSE | FALSE | 13 |
| FALSE | TRUE | 8 |
| TRUE | FALSE | 61 |
| TRUE | TRUE | 18 |
This gives us the rule
\[ \widehat{C}(x) = \begin{cases} 0 &\text{if }\text{latitude} \leq 47.5, \\ 0 &\text{otherwise} \end{cases} \]
\(\text{month} < \text{October}\)
| month_lt_oct | good_skiing | n |
|---|---|---|
| FALSE | FALSE | 12 |
| FALSE | TRUE | 8 |
| TRUE | FALSE | 62 |
| TRUE | TRUE | 18 |
This gives us the rule
\[ \widehat{C}(x) = \begin{cases} 0 &\text{if }\text{month} < \text{October}, \\ 0 &\text{otherwise} \end{cases} \]
So, if we judge purely on acuracy scores… it seems like we’re not getting anywhere here (but, we know we are getting somewhere!)
Scikit-Learn: Growing the Tree
Code
import json
import pandas as pd
import numpy as np
import sklearn
from sklearn.tree import DecisionTreeClassifier
sklearn.set_config(display='text')
ski_df = pd.read_csv("assets/ski.csv")
ski_df['good_skiing'] = ski_df['good_skiing'].astype(int)
X = ski_df[['day_num', 'latitude']]
y = ski_df['good_skiing']
dtc = DecisionTreeClassifier(
max_depth = 1,
criterion = "entropy",
random_state=5001
)
dtc.fit(X, y);
y_pred = pd.Series(dtc.predict(X), name="y_pred")
result_df = pd.concat([X,y,y_pred], axis=1)
result_df['correct'] = result_df['good_skiing'] == result_df['y_pred']
result_df.to_csv("assets/ski_predictions.csv")
sklearn.tree.plot_tree(dtc, feature_names = X.columns)
n_nodes = dtc.tree_.node_count
children_left = dtc.tree_.children_left
children_right = dtc.tree_.children_right
feature = dtc.tree_.feature
feat_index = feature[0]
feat_name = X.columns[feat_index]
thresholds = dtc.tree_.threshold
feat_threshold = thresholds[0]
#print(f"Feature: {feat_name}\nThreshold: <= {feat_threshold}")
values = dtc.tree_.value
#print(values)
dt_data = {
'feat_index': feat_index,
'feat_name': feat_name,
'feat_threshold': feat_threshold
}
dt_df = pd.DataFrame([dt_data])
dt_df.to_feather('assets/ski_dt.feather')
library(tidyverse)
library(arrow)
# Load the dataset
ski_result_df <- read_csv("assets/ski_predictions.csv")
# Load the DT info
dt_df <- read_feather("assets/ski_dt.feather")
# Here we only have one value, so just read that
# value directly
lat_thresh <- dt_df$feat_threshold
ggplot(ski_result_df, aes(x=day_num, y=latitude, color=factor(good_skiing), shape=correct)) +
geom_point(
size = g_pointsize / 1.5,
stroke = 1.5
) +
geom_hline(
yintercept = lat_thresh,
linetype = "dashed"
) +
dsan_theme("half") +
labs(
x = "Time of Year",
y = "Latitude",
color = "True Class",
#shape = "Correct?"
) +
scale_shape_manual("DT Prediction", values=c(1,3), labels=c("Incorrect","Correct")) +
scale_color_manual("True Class", values=c(cbPalette[1], cbPalette[2]), labels=c("Bad (Sunny)","Good (Snowy)"))
ski_result_df |> count(correct)
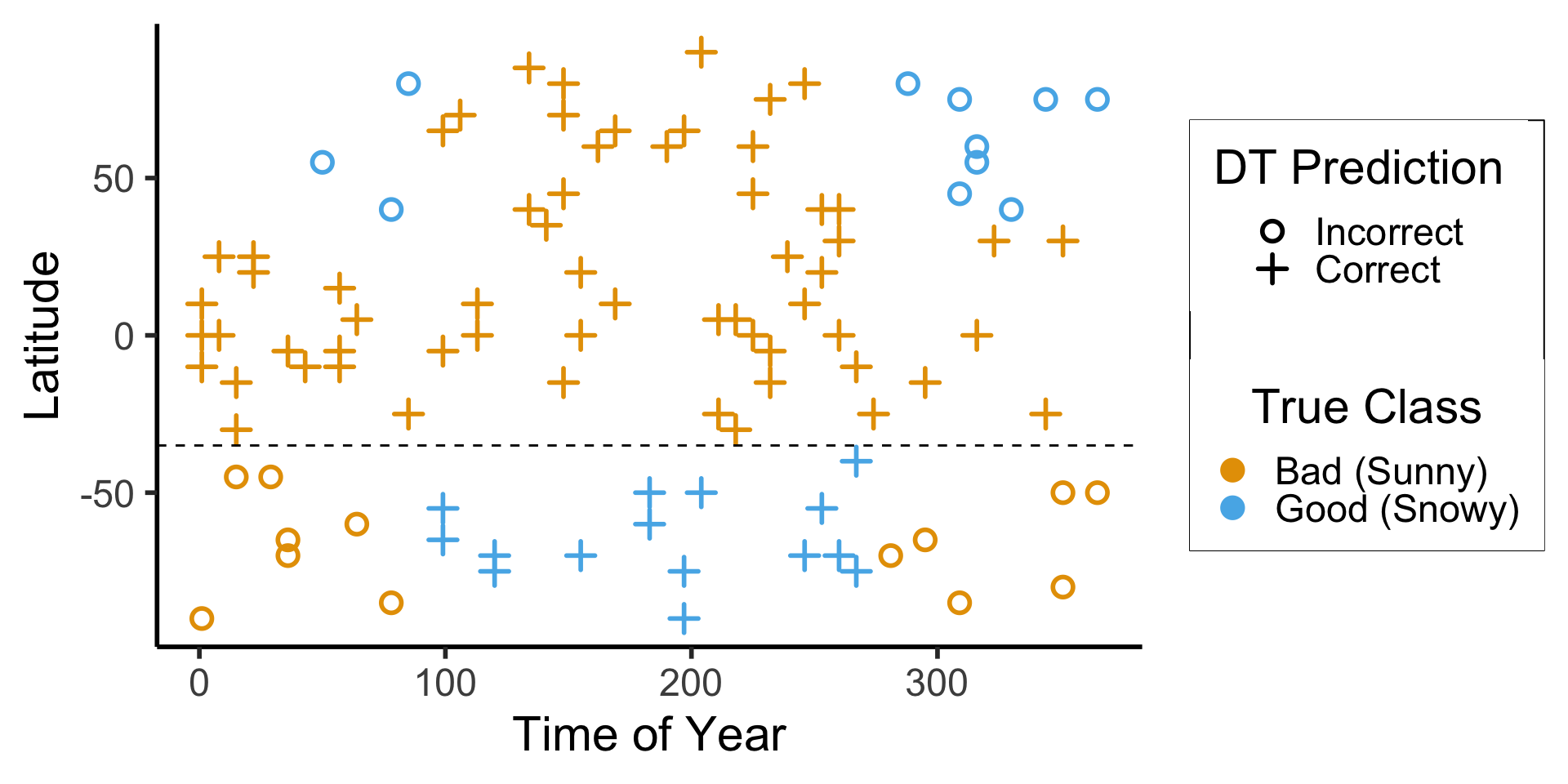
| correct | n |
|---|---|
| FALSE | 24 |
| TRUE | 76 |
\[ \begin{align*} \mathscr{L}(R_1) &= -\left[ \frac{13}{28}\log_2\left(\frac{13}{28}\right) + \frac{15}{28}\log_2\left(\frac{15}{28}\right) \right] \approx 0.996 \\ \mathscr{L}(R_2) &= -\left[ \frac{61}{72}\log_2\left(\frac{61}{72}\right) + \frac{11}{72}\log_2\left(\frac{11}{72}\right) \right] \approx 0.617 \\ %\mathscr{L}(R \rightarrow (R_1, R_2)) &= \Pr(x_i \in R_1)\mathscr{L}(R_1) + \Pr(x_i \in R_2)\mathscr{L}(R_2) \\ \mathscr{L}(R_1, R_2) &= \frac{28}{100}(0.996) + \frac{72}{100}(0.617) \approx 0.723 < 0.827~😻 \end{align*} \]
Continuous Values
- What if we replace binary labels with continuous values: in this case, cm of snow?
Code
#format_snow <- function(x) sprintf('%.2f', x)
format_snow <- function(x) round(x, 2)
ski_sample['snowfall_str'] <- sapply(ski_sample$snowfall, format_snow)
#ski_df |> head()
#print(nrow(ski_df))
ggplot(ski_sample, aes(x=day, y=latitude, label=snowfall_str)) +
geom_text(size = 6) +
dsan_theme() +
labs(
x = "Time of Year",
y = "Latitude",
shape = "Good Skiing?"
) +
scale_shape_manual(values=c(1, 3)) +
scale_x_continuous(
breaks=c(ymd('2023-01-01'), ymd('2023-02-01'), ymd('2023-03-01'), ymd('2023-04-01'), ymd('2023-05-01'), ymd('2023-06-01'), ymd('2023-07-01'), ymd('2023-08-01'), ymd('2023-09-01'), ymd('2023-10-01'), ymd('2023-11-01'), ymd('2023-12-01')),
labels=c("Jan", "Feb", "Mar", "Apr", "May", "Jun", "Jul", "Aug", "Sep", "Oct", "Nov", "Dec")
) +
scale_y_continuous(breaks=c(-90, -60, -30, 0, 30, 60, 90))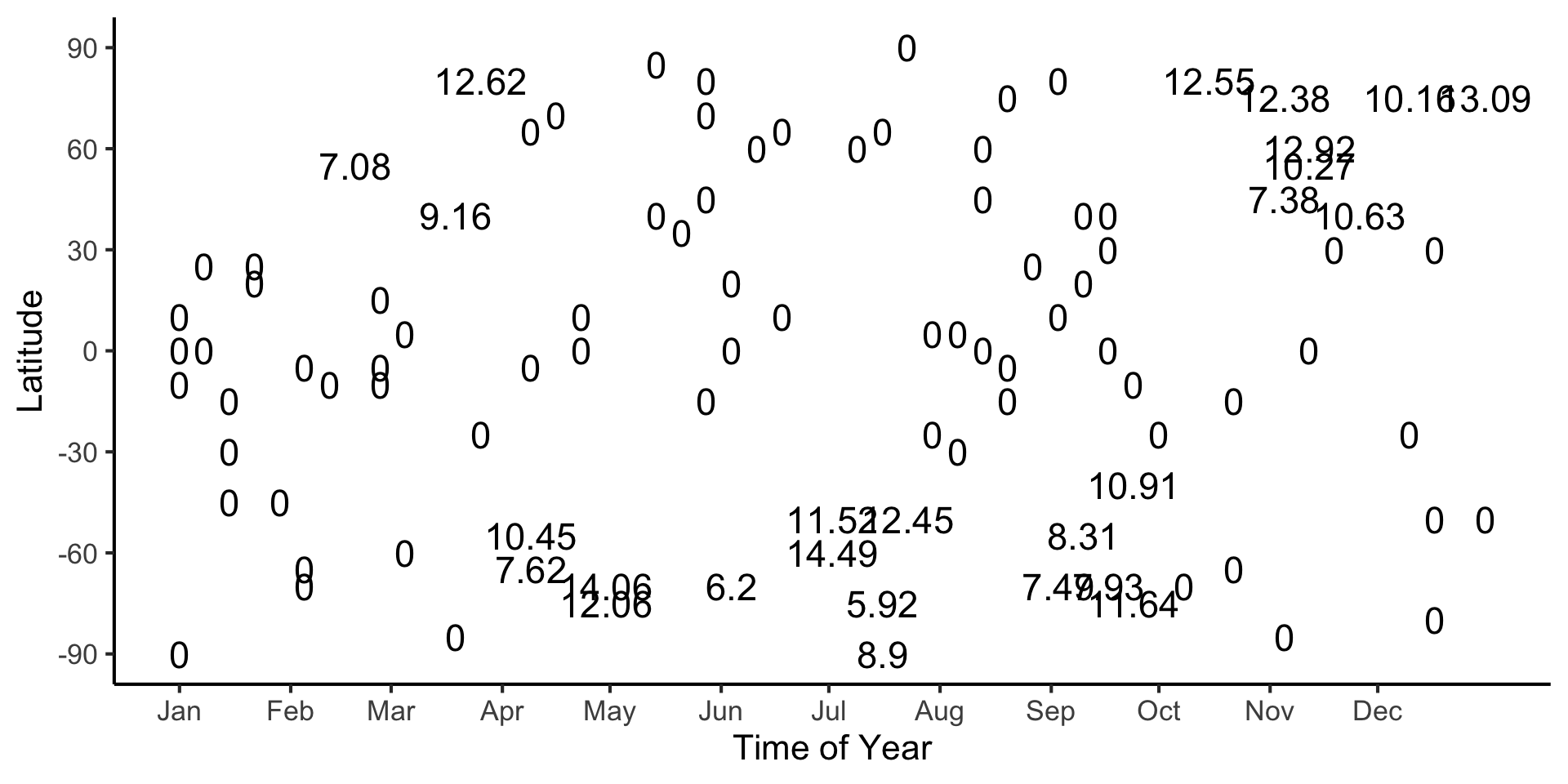
(Example adapted from CS229: Machine Learning, Stanford University)
Looking Towards Regression
- How could we make a decision tree to predict \(y\) from \(x\) for this data?
Code
library(tidyverse)
library(latex2exp)
expr_pi2 <- TeX("$\\frac{\\pi}{2}$")
expr_pi <- TeX("$\\pi$")
expr_3pi2 <- TeX("$\\frac{3\\pi}{2}$")
expr_2pi <- TeX("$2\\pi$")
x_range <- 2 * pi
x_coords <- seq(0, x_range, by = x_range / 100)
num_x_coords <- length(x_coords)
data_df <- tibble(x = x_coords)
data_df <- data_df |> mutate(
y_raw = sin(x),
y_noise = rnorm(num_x_coords, 0, 0.15)
)
data_df <- data_df |> mutate(
y = y_raw + y_noise
)
#y_coords <- y_raw_coords + y_noise
#y_coords <- y_raw_coords
#data_df <- tibble(x = x, y = y)
reg_tree_plot <- ggplot(data_df, aes(x=x, y=y)) +
geom_point(size = g_pointsize / 2) +
dsan_theme("half") +
labs(
x = "Feature",
y = "Label"
) +
geom_vline(
xintercept = pi,
linewidth = g_linewidth,
linetype = "dashed"
) +
scale_x_continuous(
breaks=c(0,pi/2,pi,(3/2)*pi,2*pi),
labels=c("0",expr_pi2,expr_pi,expr_3pi2,expr_2pi)
)
reg_tree_plot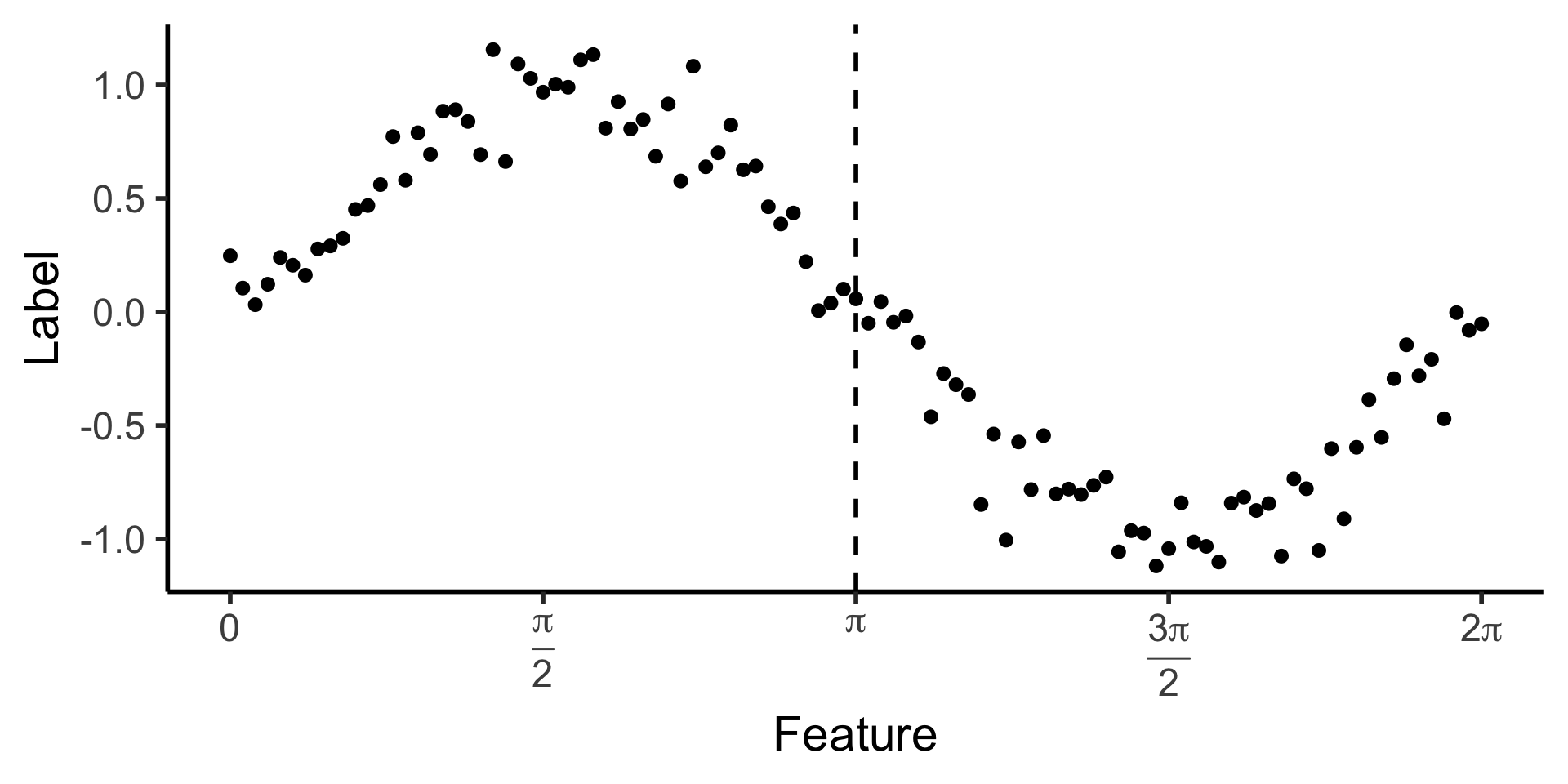
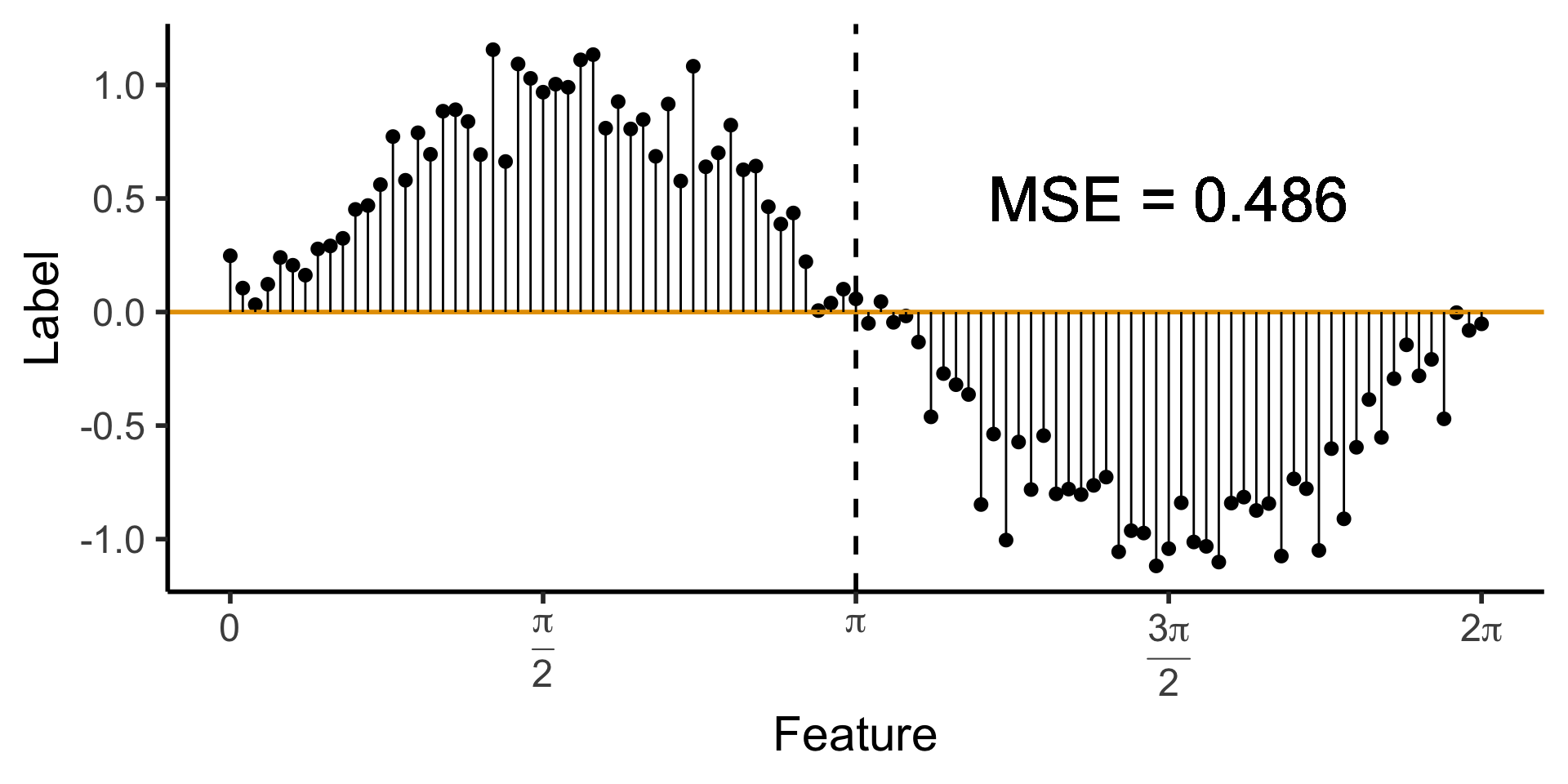
A Zero-Level Tree
- Trivial example: \(\widehat{y}(x) = 0\). How well does this do?
Code
library(ggtext)
# x_lt_pi = data_df |> filter(x < pi)
# mean(x_lt_pi$y)
data_df <- data_df |> mutate(
pred_sq_err0 = (y - 0)^2
)
mse0 <- mean(data_df$pred_sq_err0)
mse0_str <- sprintf("%.3f", mse0)
reg_tree_plot +
geom_hline(
yintercept = 0,
color=cbPalette[1],
linewidth = g_linewidth
) +
geom_segment(
aes(x=x, xend=x, y=0, yend=y)
) +
geom_text(
aes(x=(3/2)*pi, y=0.5, label=paste0("MSE = ",mse0_str)),
size = 10,
#box.padding = unit(c(2,2,2,2), "pt")
)
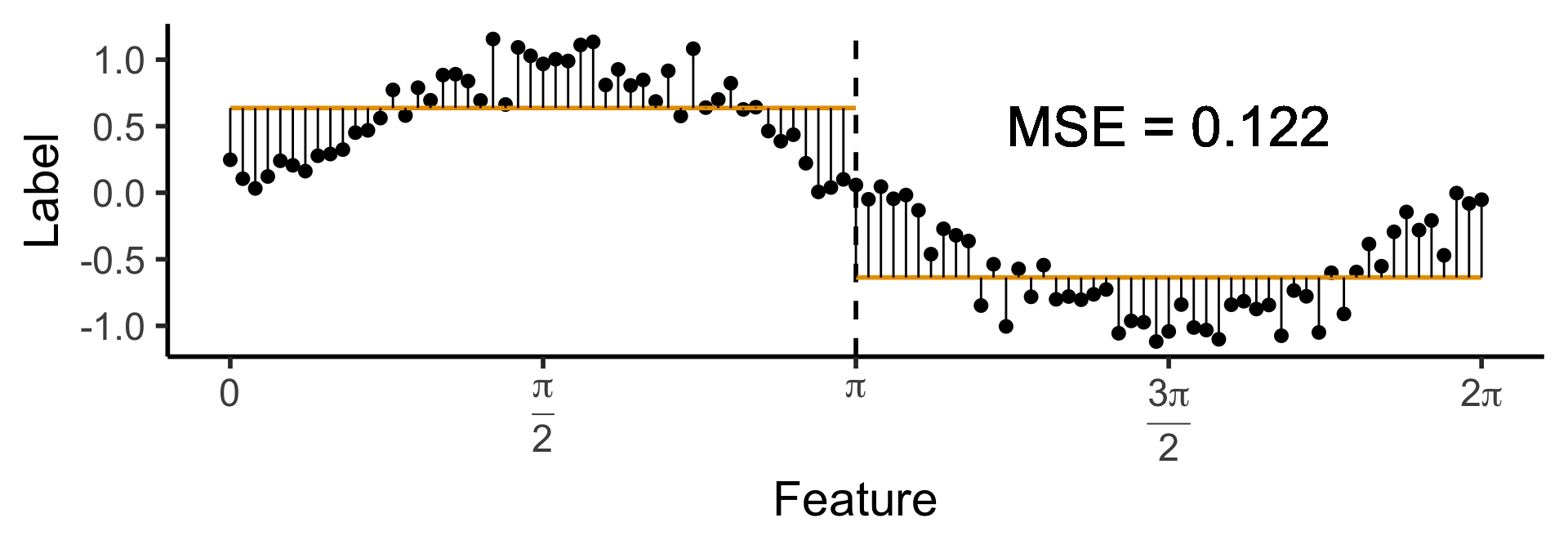
A One-Level Binary Tree
- Let’s introduce a single branch node:
\[ \widehat{y}(x) = \begin{cases} \phantom{-}\frac{2}{\pi} &\text{if }x < \pi, \\ -\frac{2}{\pi} &\text{otherwise.} \end{cases} \]
Code
get_y_pred <- function(x) ifelse(x < pi, 2/pi, -2/pi)
data_df <- data_df |> mutate(
pred_sq_err1 = (y - get_y_pred(x))^2
)
mse1 <- mean(data_df$pred_sq_err1)
mse1_str <- sprintf("%.3f", mse1)
decision_df <- tribble(
~x, ~xend, ~y, ~yend,
0, pi, 2/pi, 2/pi,
pi, 2*pi, -2/pi, -2/pi
)
reg_tree_plot +
geom_segment(
data=decision_df,
aes(x=x, xend=xend, y=y, yend=yend),
color=cbPalette[1],
linewidth = g_linewidth
) +
geom_segment(
aes(x=x, xend=x, y=get_y_pred(x), yend=y)
) +
geom_text(
aes(x=(3/2)*pi, y=0.5, label=paste0("MSE = ",mse1_str)),
size = 9,
#box.padding = unit(c(2,2,2,2), "pt")
)
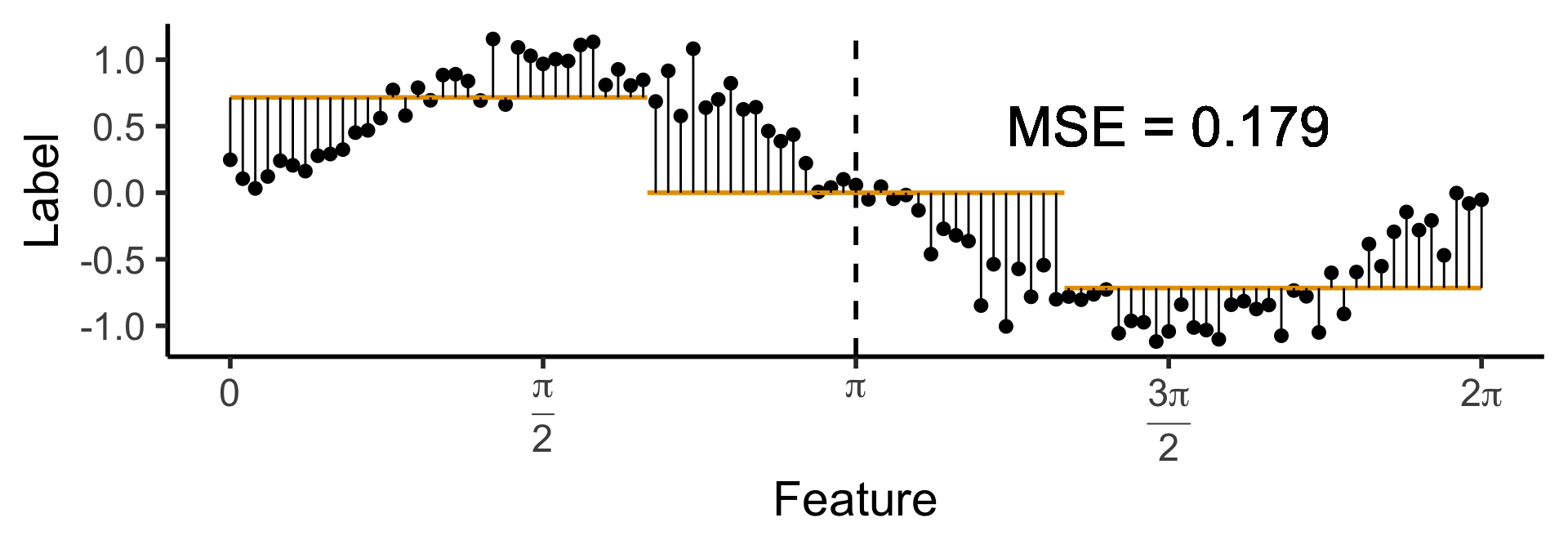
A One-Level Ternary Tree
- Now let’s allow three answers:
\[ \widehat{y}(x) = \begin{cases} \phantom{-}\frac{9}{4\pi} &\text{if }x < \frac{2\pi}{3}, \\ \phantom{-}0 &\text{if }\frac{2\pi}{3} \leq x \leq \frac{4\pi}{3} \\ -\frac{9}{4\pi} &\text{otherwise.} \end{cases} \]
Code
cut1 <- (2/3) * pi
cut2 <- (4/3) * pi
pos_mean <- 9 / (4*pi)
get_y_pred <- function(x) ifelse(x < cut1, pos_mean, ifelse(x < cut2, 0, -pos_mean))
data_df <- data_df |> mutate(
pred_sq_err1b = (y - get_y_pred(x))^2
)
mse1b <- mean(data_df$pred_sq_err1b)
mse1b_str <- sprintf("%.3f", mse1b)
decision_df <- tribble(
~x, ~xend, ~y, ~yend,
0, (2/3)*pi, pos_mean, pos_mean,
(2/3)*pi, (4/3)*pi, 0, 0,
(4/3)*pi, 2*pi, -pos_mean, -pos_mean
)
reg_tree_plot +
geom_segment(
data=decision_df,
aes(x=x, xend=xend, y=y, yend=yend),
color=cbPalette[1],
linewidth = g_linewidth
) +
geom_segment(
aes(x=x, xend=x, y=get_y_pred(x), yend=y)
) +
geom_text(
aes(x=(3/2)*pi, y=0.5, label=paste0("MSE = ",mse1b_str)),
size = 9,
#box.padding = unit(c(2,2,2,2), "pt")
)
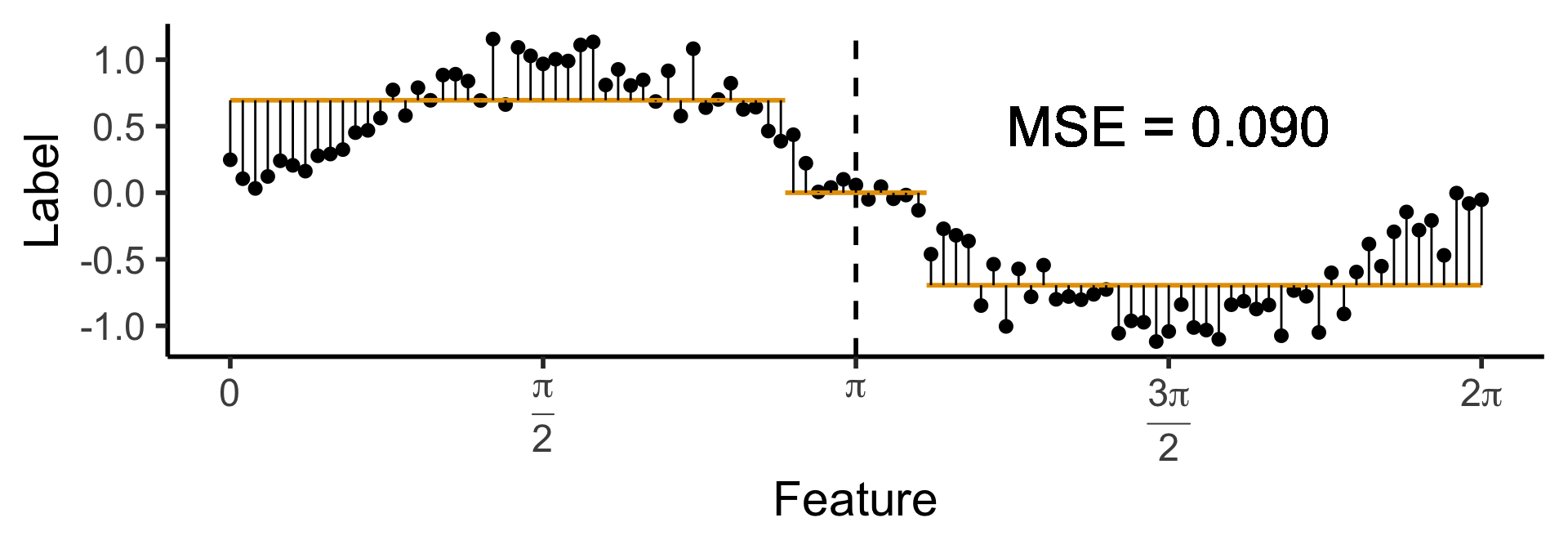
Another One-Level Ternary Tree
- Now let’s allow an uneven split:
\[ \widehat{y}(x) = \begin{cases} \phantom{-}0.695 &\text{if }x < (1-c)\pi, \\ \phantom{-}0 &\text{if }(1-c)\pi \leq x \leq (1+c)\pi \\ -0.695 &\text{otherwise,} \end{cases} \]
with \(c \approx 0.113\), gives us:
Code
c <- 0.113
cut1 <- (1 - c) * pi
cut2 <- (1 + c) * pi
pos_mean <- 0.695
get_y_pred <- function(x) ifelse(x < cut1, pos_mean, ifelse(x < cut2, 0, -pos_mean))
data_df <- data_df |> mutate(
pred_sq_err1b = (y - get_y_pred(x))^2
)
mse1b <- mean(data_df$pred_sq_err1b)
mse1b_str <- sprintf("%.3f", mse1b)
decision_df <- tribble(
~x, ~xend, ~y, ~yend,
0, cut1, pos_mean, pos_mean,
cut1, cut2, 0, 0,
cut2, 2*pi, -pos_mean, -pos_mean
)
reg_tree_plot +
geom_segment(
data=decision_df,
aes(x=x, xend=xend, y=y, yend=yend),
color=cbPalette[1],
linewidth = g_linewidth
) +
geom_segment(
aes(x=x, xend=x, y=get_y_pred(x), yend=y)
) +
geom_text(
aes(x=(3/2)*pi, y=0.5, label=paste0("MSE = ",mse1b_str)),
size = 9,
#box.padding = unit(c(2,2,2,2), "pt")
)
On to the Code!
- Scikit-learn has both
DecisionTreeClassifierandDecisionTreeRegressorclasses!
Regression Trees: Harder Task, Simpler Goal
Last week we started with classification task (of good vs. bad skiing weather), to get a feel for how decision trees approach these tasks
This week, for a deeper dive into the math/code, let’s start with regression. But why?
- Despite the fact that the task itself is harder (have to guess an output \(\ell \in \mathbb{R}\) rather than \(\ell \in \{0, 1\}\)),
- Our objective/goal is easier to define: given feature matrix \(\mathbf{X} = [\begin{smallmatrix}X_1 & \cdots & X_n\end{smallmatrix}]\) and labels \(\boldsymbol\ell = (\ell_1, \ldots, \ell_n)^\top\), find a function \(\widehat{f}\) which minimizes
\[ \mathscr{L}_{\text{MSE}}\left(\widehat{f}~\right) = \sum_{i=1}^N \left(\widehat{f}(X_i) - \ell_i\right)^2 \]
Once we’re comfortable with how to approach this regression task, we’ll move back to the classification task, where there is no longer a single “obvious” choice for the loss function \(\mathscr{L}\left(\widehat{f}~\right)\)
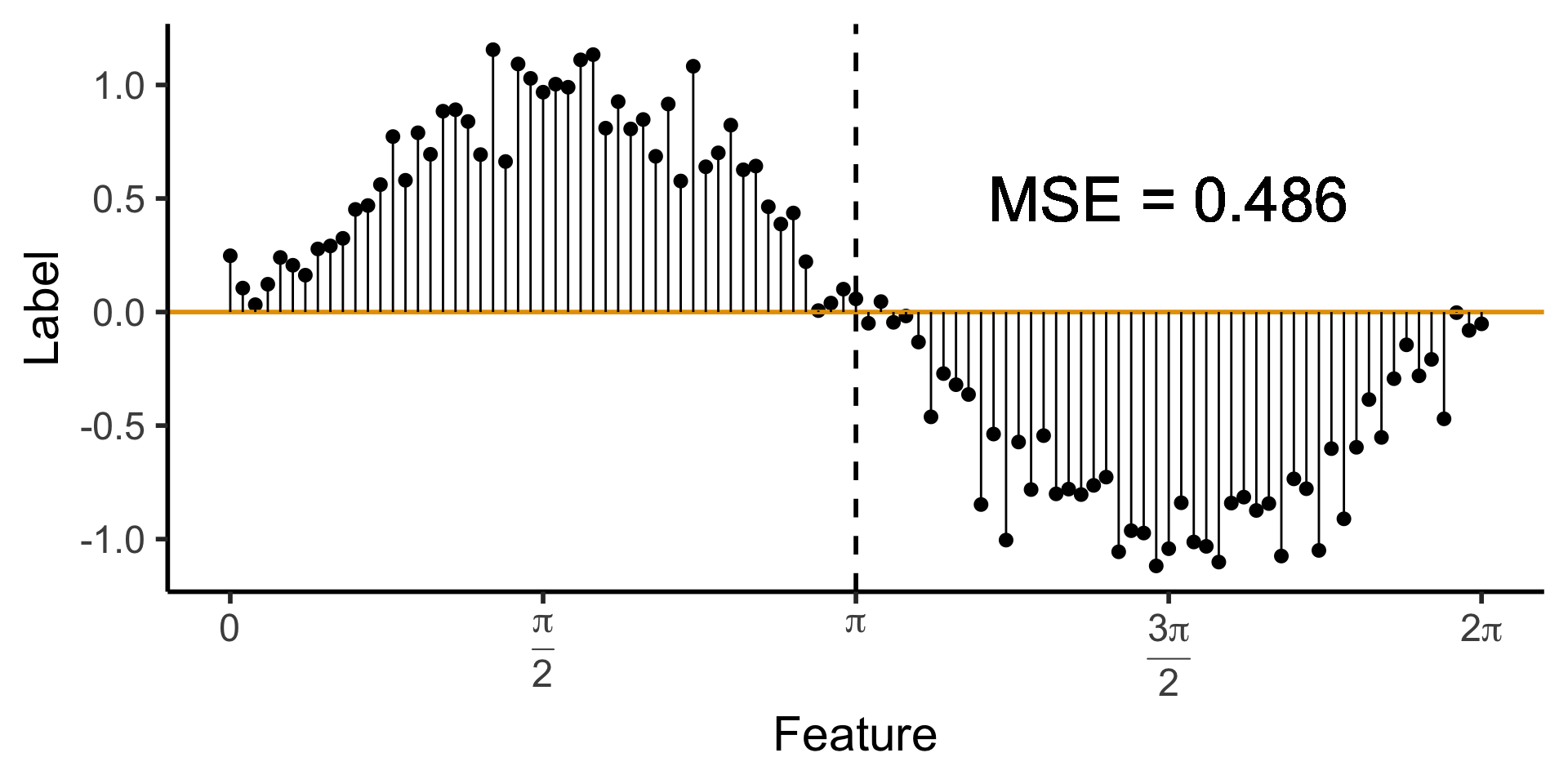
A Zero-Level Tree
- Trivial example: \(\widehat{y}(x) = 0\). (We ignore the feature value)
- How well does this do?
Code
library(ggtext)
# x_lt_pi = data_df |> filter(x < pi)
# mean(x_lt_pi$y)
data_df <- data_df |> mutate(
pred_sq_err0 = (y - 0)^2
)
mse0 <- mean(data_df$pred_sq_err0)
mse0_str <- sprintf("%.3f", mse0)
reg_tree_plot +
geom_hline(
yintercept = 0,
color=cbPalette[1],
linewidth = g_linewidth
) +
geom_segment(
aes(x=x, xend=x, y=0, yend=y)
) +
geom_text(
aes(x=(3/2)*pi, y=0.5, label=paste0("MSE = ",mse0_str)),
size = 10,
#box.padding = unit(c(2,2,2,2), "pt")
)
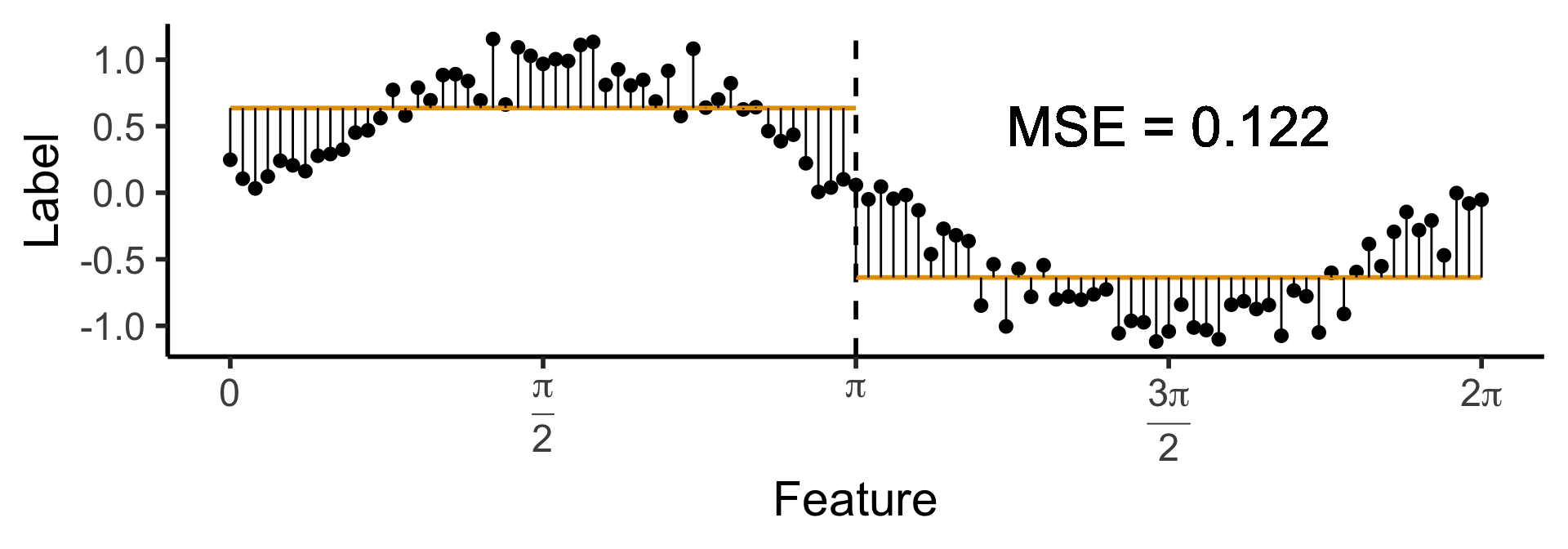
A One-Level Binary Tree
- Let’s introduce a single branch node:
\[ \widehat{y}(x) = \begin{cases} \phantom{-}\frac{2}{\pi} &\text{if }x < \pi, \\ -\frac{2}{\pi} &\text{otherwise.} \end{cases} \]
Code
get_y_pred <- function(x) ifelse(x < pi, 2/pi, -2/pi)
data_df <- data_df |> mutate(
pred_sq_err1 = (y - get_y_pred(x))^2
)
mse1 <- mean(data_df$pred_sq_err1)
mse1_str <- sprintf("%.3f", mse1)
decision_df <- tribble(
~x, ~xend, ~y, ~yend,
0, pi, 2/pi, 2/pi,
pi, 2*pi, -2/pi, -2/pi
)
reg_tree_plot +
geom_segment(
data=decision_df,
aes(x=x, xend=xend, y=y, yend=yend),
color=cbPalette[1],
linewidth = g_linewidth
) +
geom_segment(
aes(x=x, xend=x, y=get_y_pred(x), yend=y)
) +
geom_text(
aes(x=(3/2)*pi, y=0.5, label=paste0("MSE = ",mse1_str)),
size = 9,
#box.padding = unit(c(2,2,2,2), "pt")
)
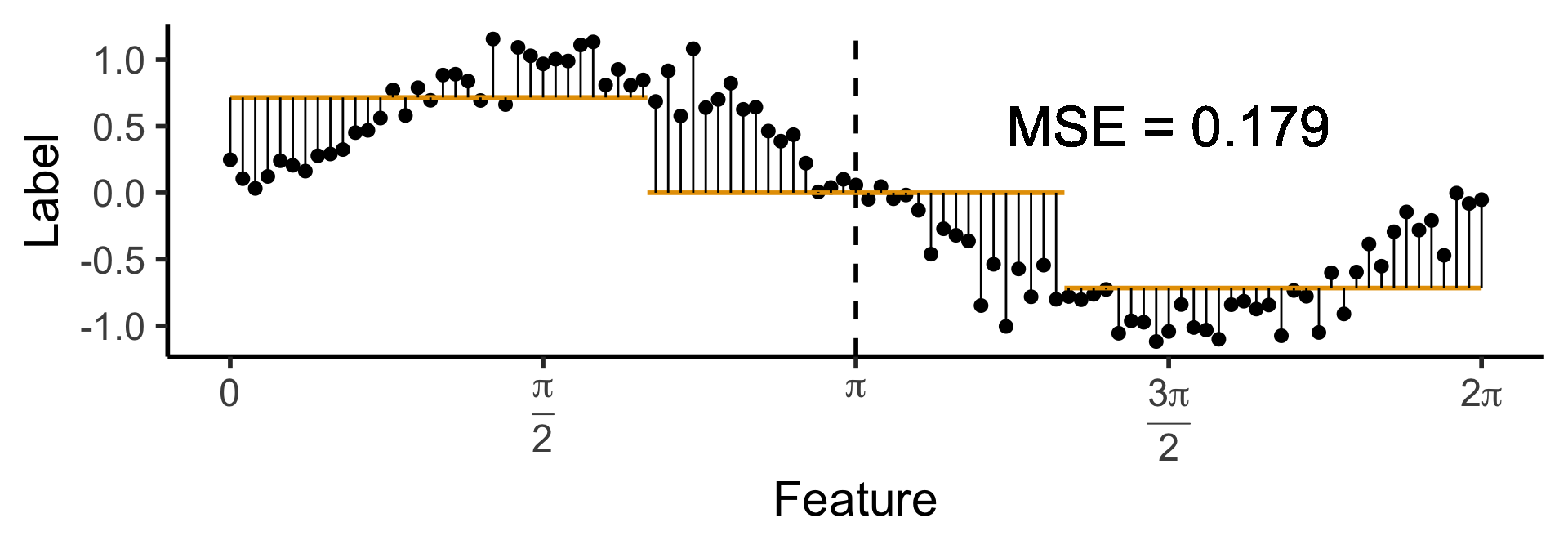
A One-Level Ternary Tree
- Now let’s allow three answers:
\[ \widehat{y}(x) = \begin{cases} \phantom{-}\frac{9}{4\pi} &\text{if }x < \frac{2\pi}{3}, \\ \phantom{-}0 &\text{if }\frac{2\pi}{3} \leq x \leq \frac{4\pi}{3} \\ -\frac{9}{4\pi} &\text{otherwise.} \end{cases} \]
Code
cut1 <- (2/3) * pi
cut2 <- (4/3) * pi
pos_mean <- 9 / (4*pi)
get_y_pred <- function(x) ifelse(x < cut1, pos_mean, ifelse(x < cut2, 0, -pos_mean))
data_df <- data_df |> mutate(
pred_sq_err1b = (y - get_y_pred(x))^2
)
mse1b <- mean(data_df$pred_sq_err1b)
mse1b_str <- sprintf("%.3f", mse1b)
decision_df <- tribble(
~x, ~xend, ~y, ~yend,
0, (2/3)*pi, pos_mean, pos_mean,
(2/3)*pi, (4/3)*pi, 0, 0,
(4/3)*pi, 2*pi, -pos_mean, -pos_mean
)
reg_tree_plot +
geom_segment(
data=decision_df,
aes(x=x, xend=xend, y=y, yend=yend),
color=cbPalette[1],
linewidth = g_linewidth
) +
geom_segment(
aes(x=x, xend=x, y=get_y_pred(x), yend=y)
) +
geom_text(
aes(x=(3/2)*pi, y=0.5, label=paste0("MSE = ",mse1b_str)),
size = 9,
#box.padding = unit(c(2,2,2,2), "pt")
)
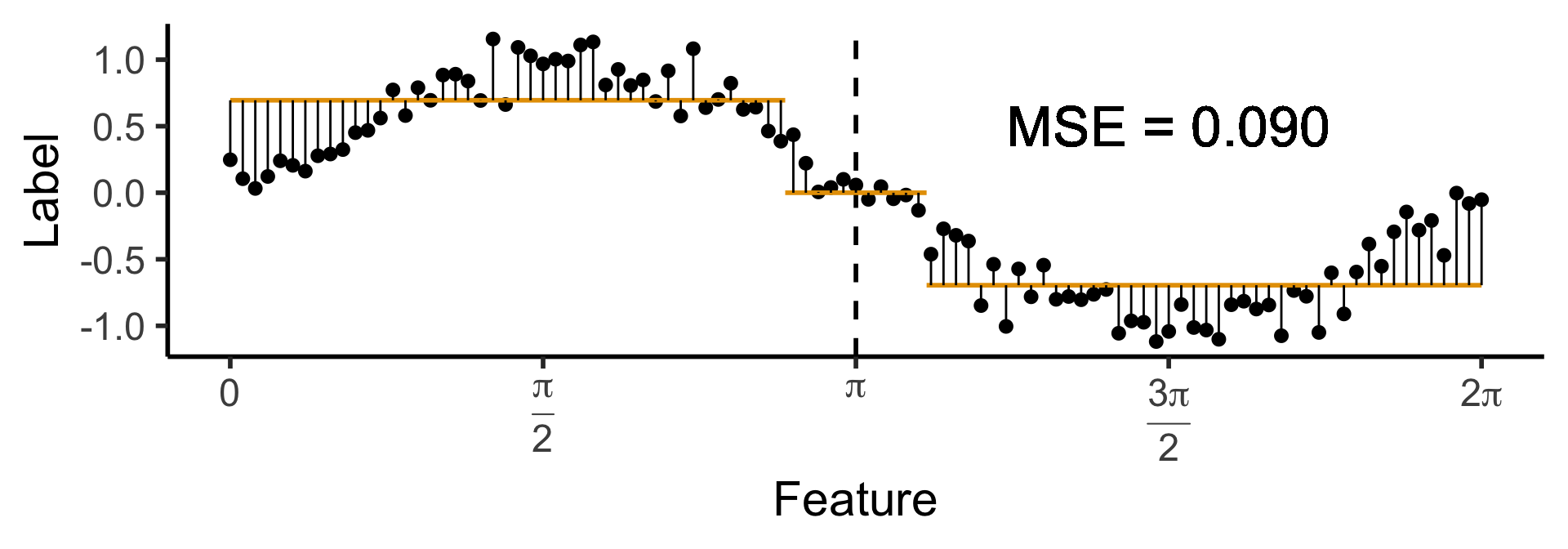
Another One-Level Ternary Tree
- Now let’s allow an uneven split:
\[ \widehat{y}(x) = \begin{cases} \phantom{-}0.695 &\text{if }x < (1-c)\pi, \\ \phantom{-}0 &\text{if }(1-c)\pi \leq x \leq (1+c)\pi \\ -0.695 &\text{otherwise,} \end{cases} \]
with \(c \approx 0.113\), gives us:
Code
c <- 0.113
cut1 <- (1 - c) * pi
cut2 <- (1 + c) * pi
pos_mean <- 0.695
get_y_pred <- function(x) ifelse(x < cut1, pos_mean, ifelse(x < cut2, 0, -pos_mean))
data_df <- data_df |> mutate(
pred_sq_err1b = (y - get_y_pred(x))^2
)
mse1b <- mean(data_df$pred_sq_err1b)
mse1b_str <- sprintf("%.3f", mse1b)
decision_df <- tribble(
~x, ~xend, ~y, ~yend,
0, cut1, pos_mean, pos_mean,
cut1, cut2, 0, 0,
cut2, 2*pi, -pos_mean, -pos_mean
)
reg_tree_plot +
geom_segment(
data=decision_df,
aes(x=x, xend=xend, y=y, yend=yend),
color=cbPalette[1],
linewidth = g_linewidth
) +
geom_segment(
aes(x=x, xend=x, y=get_y_pred(x), yend=y)
) +
geom_text(
aes(x=(3/2)*pi, y=0.5, label=paste0("MSE = ",mse1b_str)),
size = 9,
#box.padding = unit(c(2,2,2,2), "pt")
)
Onto Classification
- We’d like to carry out a similar process for classification tasks: (1) try a split of the full space into \(K\) sub-regions, then (2) evaluate the split based on how much it reduces uncertainty
- But, the discreteness of labels in this case means we cannot just “import” MSE as our loss function
- For example, if the true class for a datapoint \(i\) is \(\ell_i = 1\), is a guess \(\widehat{\ell} = 3\) “twice as wrong” as \(\widehat{\ell} = 2\)?
- So, let’s brainstorm a discrete loss function
Getting Closer
- Your first instinct might be to choose the misclassification rate, the proportion of points in region \(R\) that we are misclassifying if we guess the most-common class:
\[ \mathscr{L}_{MC}(R) = 1 - \widehat{p}_{R} \]
- The shape of this function, however, gives us a hint as to why we may want to choose a different function:
Code
library(tidyverse)
library(latex2exp)
my_mc <- function(p) 0.5 - abs(0.5 - p)
x_vals <- seq(0, 1, 0.01)
mc_vals <- sapply(x_vals, my_mc)
phat_label <- TeX('$\\widehat{p}$')
data_df <- tibble(x=x_vals, loss_mc=mc_vals)
ggplot(data_df, aes(x=x, y=loss_mc)) +
geom_line(linewidth = g_linewidth) +
dsan_theme("half") +
labs(
x = phat_label,
y = "Misclassification Loss"
)
Using Misclassification Loss to Choose a Split
- Given a parent region \(R_P\), we’re trying to choose a split into subregions \(R_1\) and \(R_2\) which will decrease the loss: \(\frac{|R_1|}{|R_P|}\mathscr{L}(R_1) + \frac{|R_2|}{|R_P|}\mathscr{L}(R_2) < \mathscr{L}(R_P)\)
- But what happens when we use misclassification loss to “judge” a split?
- Tl;dr this doesn’t “detect” when we’ve reduced uncertainty
- But we do have a function that was constructed to measure uncertainty!
Using Entropy to Choose a Split
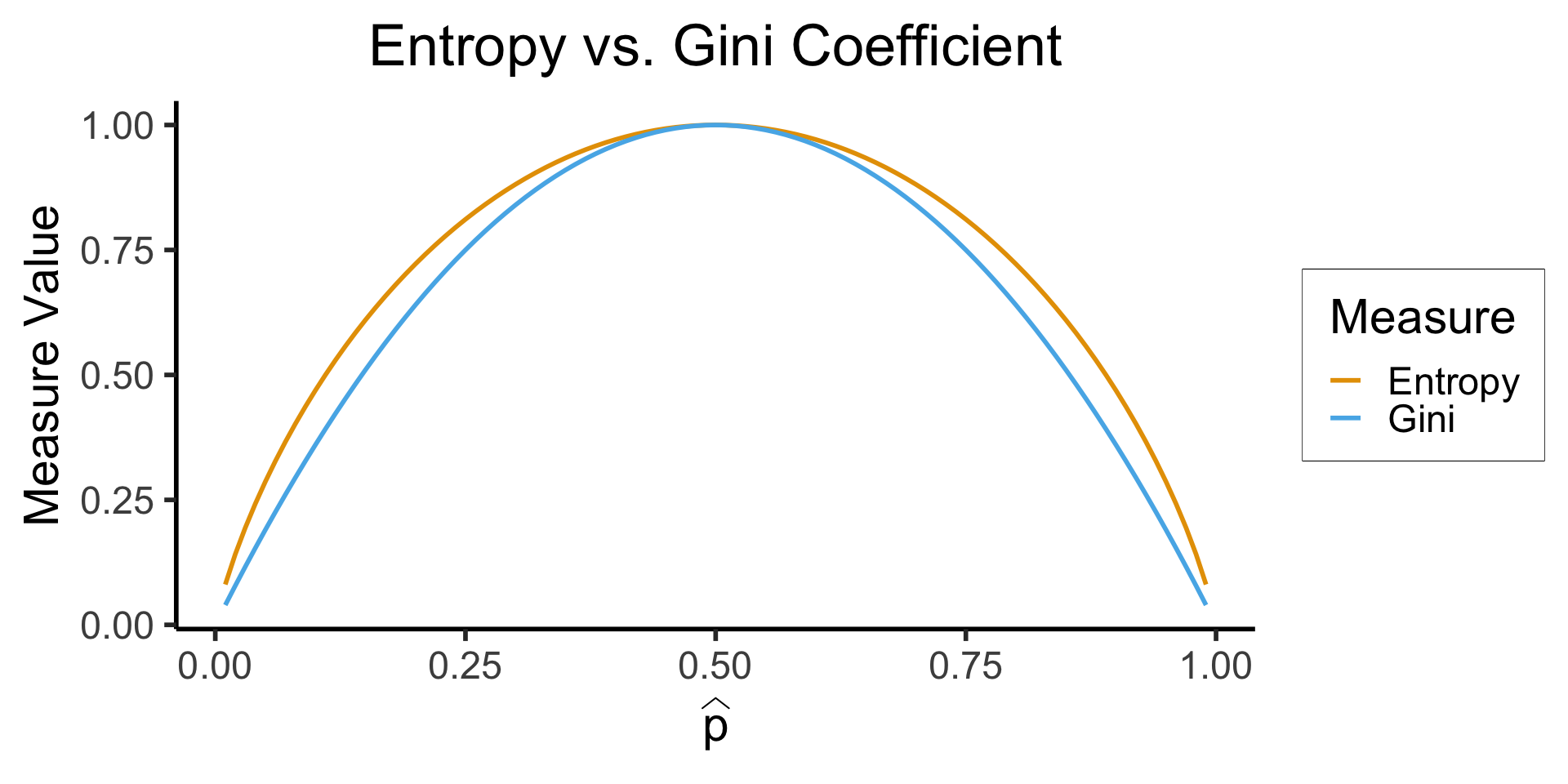
Is There Another Option?
\[ \mathscr{L}_{\text{Ent}}(\widehat{p}) = -\sum_{i=1}^K \widehat{p}_k\log_2(\widehat{p}_k) \]
\[ \mathscr{L}_{\text{Gini}}(\widehat{p}) = -\sum_{i=1}^K \widehat{p}_k(1-\widehat{p}_k) \]
Code
library(tidyverse)
library(latex2exp)
phat_label <- TeX('$\\widehat{p}')
my_ent <- function(p) -(p*log2(p) + (1-p)*log2(1-p))
my_gini <- function(p) 4*p*(1-p)
x_vals <- seq(0.01, 0.99, 0.01)
ent_vals <- sapply(x_vals, my_ent)
ent_df <- tibble(x=x_vals, y=ent_vals, Measure="Entropy")
gini_vals <- sapply(x_vals, my_gini)
gini_df <- tibble(x=x_vals, y=gini_vals, Measure="Gini")
data_df <- bind_rows(ent_df, gini_df)
ggplot(data=data_df, aes(x=x, y=y, color=Measure)) +
geom_line(linewidth = g_linewidth) +
dsan_theme("half") +
scale_color_manual(values=c(cbPalette[1], cbPalette[2])) +
labs(
x = phat_label,
y = "Measure Value",
title = "Entropy vs. Gini Coefficient"
)
The Space of All Decision Trees
- Why can’t we just try all possible decision trees, and choose the one with minimum loss? Consider a case with just \(N = 1\) binary feature, \(F_1 \in \{0, 1\}\):
Decision Trees \(\leftrightarrow\) Binary Functions
- Possible binary decision trees over \(N\) binary features \(\leftrightarrow\) possible binary functions mapping all \(2^N\) possible inputs to an output \(\widehat{\ell} \in \{0,1\}\)
- That is, all functions \(f: 2^N \rightarrow \{0,1\}\). There are \(2^{2^N}\) such functions 😵💫
- Previous slide:
- \(T_0 = \{(f_1 = 0) \rightarrow 0, (f_1 = 1) \rightarrow 0\}\)
- \(T_1 = \{(f_1 = 0) \rightarrow 1, (f_1 = 1) \rightarrow 1\}\)
- \(T_2 = \{(f_1 = 0) \rightarrow 0, (f_1 = 1) \rightarrow 1\}\)
- \(T_3 = \{(f_1 = 0) \rightarrow 1, (f_1 = 1) \rightarrow 0\}\)
- With \(N = 2\) binary features, each tree would choose a possible decision for inputs \((f_1 = 0, f_2 = 0)\), \((f_1 = 0, f_2 = 1)\), \((f_1 = 1, f_2 = 0)\), \((f_1 = 1, f_2 = 1)\)
- Possible binary DTs over \(N\) ternary (3-class) features \(\leftrightarrow\) map all \(3^N\) inputs to output \(\widehat{\ell} \in \{0, 1\} \implies 2^{3^N}\) ternary DTs… Ternary DTs, \(N\) ternary features \(\implies\) \(3^{3^N}\) DTs
So What Do We Do Instead?
- We get greedy!
- Start from the top of the tree, and at each level, choose feature \(j^*\) and splitpoint \(s^*\) as solution to:
\[ (j^*, s^*) = \argmax_{j, s}\left[ \mathscr{L}(R_1(j,s)) + \mathscr{L}(R_2(j,s)) \right], \]
where
\[ R_1(j, s) = \{X \mid X_j < s\}, \; R_2(j, s) = \{X \mid X_j \geq s\}. \]
Back to the Skiing Example
Code
library(tidyverse)
library(lubridate)
set.seed(5001)
sample_size <- 100
day <- seq(ymd('2023-01-01'),ymd('2023-12-31'),by='weeks')
lat_bw <- 5
latitude <- seq(-90, 90, by=lat_bw)
ski_df <- expand_grid(day, latitude)
ski_df <- tibble::rowid_to_column(ski_df, var='obs_id')
#ski_df |> head()
# Data-generating process
lat_cutoff <- 35
ski_df <- ski_df |> mutate(
near_equator = abs(latitude) <= lat_cutoff,
northern = latitude > lat_cutoff,
southern = latitude < -lat_cutoff,
first_3m = day < ymd('2023-04-01'),
last_3m = day >= ymd('2023-10-01'),
middle_6m = (day >= ymd('2023-04-01')) & (day < ymd('2023-10-01')),
snowfall = 0
)
# Update the non-zero sections
mu_snow <- 10
sd_snow <- 2.5
# How many northern + first 3 months
num_north_first_3 <- nrow(ski_df[ski_df$northern & ski_df$first_3m,])
ski_df[ski_df$northern & ski_df$first_3m, 'snowfall'] = rnorm(num_north_first_3, mu_snow, sd_snow)
# Northerns + last 3 months
num_north_last_3 <- nrow(ski_df[ski_df$northern & ski_df$last_3m,])
ski_df[ski_df$northern & ski_df$last_3m, 'snowfall'] = rnorm(num_north_last_3, mu_snow, sd_snow)
# How many southern + middle 6 months
num_south_mid_6 <- nrow(ski_df[ski_df$southern & ski_df$middle_6m,])
ski_df[ski_df$southern & ski_df$middle_6m, 'snowfall'] = rnorm(num_south_mid_6, mu_snow, sd_snow)
# And collapse into binary var
ski_df['good_skiing'] = ski_df$snowfall > 0
# This converts day into an int
ski_df <- ski_df |> mutate(
day_num = lubridate::yday(day)
)
#print(nrow(ski_df))
ski_sample <- ski_df |> slice_sample(n = sample_size)
ski_sample |> write_csv("assets/ski.csv")
month_vec <- c(ymd('2023-01-01'), ymd('2023-02-01'), ymd('2023-03-01'), ymd('2023-04-01'), ymd('2023-05-01'), ymd('2023-06-01'), ymd('2023-07-01'), ymd('2023-08-01'), ymd('2023-09-01'), ymd('2023-10-01'), ymd('2023-11-01'), ymd('2023-12-01'))
month_labels <- c("Jan", "Feb", "Mar", "Apr", "May", "Jun", "Jul", "Aug", "Sep", "Oct", "Nov", "Dec")
lat_vec <- c(-90, -60, -30, 0, 30, 60, 90)
ggplot(
ski_sample,
aes(
x=day,
y=latitude,
#shape=good_skiing,
color=good_skiing
)) +
geom_point(
size = g_pointsize / 1.5,
#stroke=1.5
) +
dsan_theme() +
labs(
x = "Time of Year",
y = "Latitude",
shape = "Good Skiing?"
) +
scale_shape_manual(name="Good Skiing?", values=c(1, 3)) +
scale_color_manual(name="Good Skiing?", values=c(cbPalette[1], cbPalette[2]), labels=c("No (Sunny)","Yes (Snowy)")) +
scale_x_continuous(
breaks=c(month_vec,ymd('2024-01-01')),
labels=c(month_labels,"Jan")
) +
scale_y_continuous(breaks=lat_vec)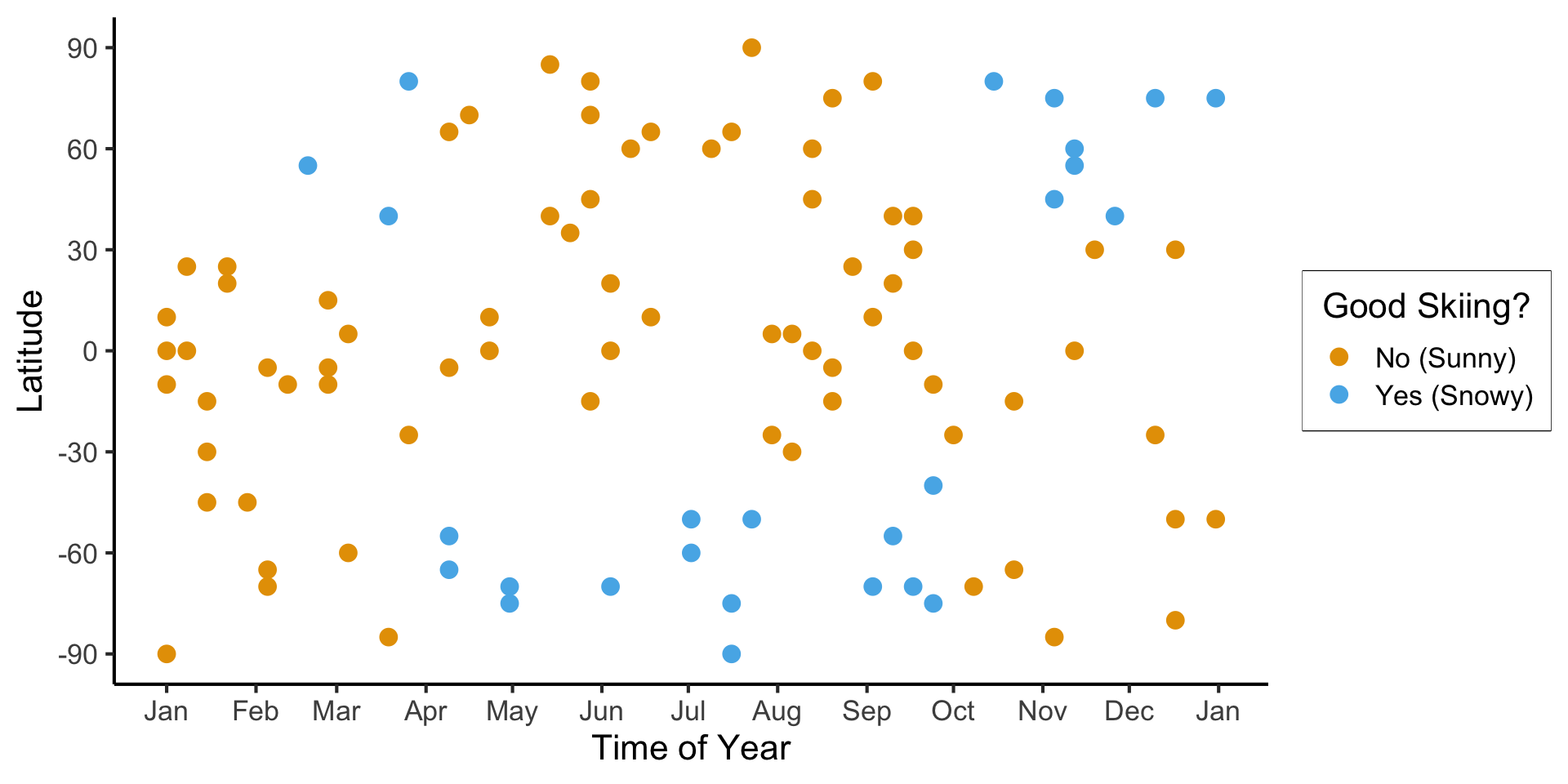
(Example adapted from CS229: Machine Learning, Stanford University)
The Parent Region
- Starting out: no splits at all, so that \(R = \{X_i \mid X_i \in \mathbf{X} \}\)
- So we just guess most frequent class in the dataset: bad skiing
- This gives us \(\Pr(\text{Correct Guess} \mid \text{Guess Bad}) = 0.74\)
- Since we’re not splitting the region up at all (yet), the entropy is just
\[ \mathscr{L}(R_i) = -[(0.74)\log_2(0.74) + (0.26)\log_2(0.26)] \approx 0.8267 \]
Judging Split Options
Given that \(\mathscr{L}(R_P) \approx 0.9427\), let’s think through two choices for the first split:
Code
ski_sample <- ski_sample |> mutate(
lat_lt_n425 = latitude < -42.5
)
r1a <- ski_sample |> filter(lat_lt_n425) |> summarize(
good_skiing = sum(good_skiing),
total = n()
) |> mutate(region = "R1(A)", .before=good_skiing)
r2a <- ski_sample |> filter(lat_lt_n425 == FALSE) |> summarize(
good_skiing = sum(good_skiing),
total = n()
) |> mutate(region = "R2(A)", .before=good_skiing)
choice_a_df <- bind_rows(r1a, r2a)
choice_a_df
ski_sample <- ski_sample |> mutate(
month_lt_oct = day < ymd('2023-10-01')
)
r1b <- ski_sample |> filter(month_lt_oct) |> summarize(
good_skiing = sum(good_skiing),
total = n()
) |> mutate(region = "R1(B)", .before=good_skiing)
r2b <- ski_sample |> filter(month_lt_oct == FALSE) |> summarize(
good_skiing = sum(good_skiing),
total = n()
) |> mutate(region = "R2(B)", .before=good_skiing)
choice_b_df <- bind_rows(r1b, r2b)
choice_b_df\[ \begin{align*} R_1^A &= \{X_i \mid X_{i,\text{lat}} < -42.5\} \\ R_2^A &= \{X_i \mid X_{i,\text{lat}} \geq -42.5\} \end{align*} \]
| region | good_skiing | total |
|---|---|---|
| R1(A) | 14 | 27 |
| R2(A) | 12 | 73 |
\[ \begin{align*} \mathscr{L}(R_1^A) &= -\mkern-4mu\left[ \frac{21}{32}\log_2\frac{21}{32} + \frac{11}{32}\log_2\frac{11}{32} \right] \approx 0.9284 \\ \mathscr{L}(R_2^A) &= -\mkern-4mu\left[ \frac{15}{68}\log_2\frac{15}{68} + \frac{53}{68}\log_2\frac{53}{68}\right] \approx 0.7612 \\ \implies \mathscr{L}(A) &= \frac{32}{100}(0.9284) + \frac{68}{100}(0.7612) \approx 0.8147 % < 0.9427 \end{align*} \]
\[ \begin{align*} R_1^B &= \{X_i \mid X_{i,\text{month}} < \text{October}\} \\ R_2^B &= \{X_i \mid X_{i,\text{month}} \geq \text{October}\} \end{align*} \]
| region | good_skiing | total |
|---|---|---|
| R1(B) | 18 | 80 |
| R2(B) | 8 | 20 |
\[ \begin{align*} \mathscr{L}(R_1^B) &= -\mkern-4mu\left[ \frac{28}{75}\log_2\frac{28}{75} + \frac{47}{75}\log_2\frac{47}{75}\right] \approx 0.9532 \\ \mathscr{L}(R_2^B) &= -\mkern-4mu\left[ \frac{8}{25}\log_2\frac{8}{25} + \frac{17}{25}\log_2\frac{17}{25} \right] \approx 0.9044 \\ \implies \mathscr{L}(B) &= \frac{75}{100}(0.9532) + \frac{25}{100}(0.9044) \approx 0.941 \end{align*} \]
- Notice: \(\mathscr{L}(A)\), \(\mathscr{L}(B)\) both \(< \mathscr{L}(R_P)\). But \(\mathscr{L}(R_P) - \mathscr{L}(A) = 0.128\), \(\mathscr{L}(R_P) - \mathscr{L}(B) = 0.0017\). \(B\) decreases our uncertainty more than \(A\), given \(R_P\).
When Do We Stop?
- Option 1: Stop when all nodes are pure; there is no uncertainty left
- Pros: Perfect training accuracy!
- Cons: The definition of overfitting
- Option 2: Manually restrict the number of levels, via a hyperparameter (could be
max_levels, ormin_samples_leaf) - Option 3: Prune the tree using heuristic methods
Random Forests
The Wisdom of Crowds
- Imagine you’re assembling a darts team. You can choose a team of 4 from among the following 8 players:
| Player | Skill |
|---|---|
| Larry “Lefty” Lechuga | Always hits 5cm left of bullseye |
| Rico Righty | Always hits 5cm right of bullseye |
| Lil Uppy Vert | Always hits 5cm above bullseye |
| Inconsistent Inkyung | Hits bullseye 50% of time, other 50% hits random point |
| Diagonal Dave | Always hits 5cm above right of bullseye |
| Dobert Downy Jr. | Always hits 5cm below bullseye |
| Gregor “the GOAT” Gregorsson | Hits bullseye 99.9% of time, other 0.1% hits random point |
| Craig | Top 25 Craigs of 2023 |
Your Opponents

High Variance, Low Bias
The Wisdom of Sheep
- Unfortunately, the “wisdom of crowds” phenomenon only works if everyone in the crowd is unable to communicate
- The minute people tasked with making decisions as a group begin to communicate (long story short), they begin to follow charismatic leaders
![]() , and the effect goes away (biases no longer cancel out)
, and the effect goes away (biases no longer cancel out) - The takeaway for effectively training random forests: ensure that each tree has a separate (ideally orthogonal) slice of the full dataset, and has to infer labels from only that slice!
Bagging and Boosting
Decision Trees: What Now?
- We have a dataset and a decision tree… now what?
- If our only goal is interpretability, we’re done
- If we want to increase accuracy/efficiency, however, we can do better!
Bootstrapped Trees
Making up for Lost Interpretability
- While we no longer have a nice single tree structure, we can still “back out” the most important features!
- Basic idea: for importance of feature \(j\), loop over all subtrees, and look at the average decrease in uncertainty when a tree splits on feature \(j\)
Doing Even Better
- Issue: Each bootstrapped tree will be highly correlated
- If there is one extremely strong signal (think of the RateMyProfessors example!), associated with one (or a few) feature(s), all of the trees will focus on that feature
- How can we ensure that some trees pick up on more subtle signals within the dataset?
Decorrelating Trees
- Long story short: give each subtree only a subset of the features, of size \(M_i \approx \sqrt{M}\)
- Can prove that:
- Smaller subsets \(\implies\) too much uncorrelated info to aggregate
- Larger subsets \(\implies\) trees become correlated
But Wait…
- We’re giving each subtree a portion of the features, hoping that each one picks up on some important “sub-signal” in the data
- Instead of hoping, why don’t we make sure that each subtree is tasked with explaining the so-far-unexplained variation?
- Enter boosting 😎
Boosting
- Rather than giving each subtree a random subset of features, grow trees sequentially! Ask each subtree to explain remaining unexplained variance from previous step
- Step 1: \(\widehat{f}_1(X)\) = DT for \(X \rightarrow Y\)
- Step \(t+1\): \(\widehat{f}_{t+1}(X)\) = DT for \(X \rightarrow \left(\widehat{f}_t(X) - Y\right)\)
Code
library(ggtext)
# x_lt_pi = data_df |> filter(x < pi)
# mean(x_lt_pi$y)
data_df <- data_df |> mutate(
pred_sq_err0 = (y - 0)^2
)
mse0 <- mean(data_df$pred_sq_err0)
mse0_str <- sprintf("%.3f", mse0)
reg_tree_plot +
geom_hline(
yintercept = 0,
color=cbPalette[1],
linewidth = g_linewidth
) +
geom_segment(
aes(x=x, xend=x, y=0, yend=y)
) +
geom_text(
aes(x=(3/2)*pi, y=0.5, label=paste0("MSE = ",mse0_str)),
size = 10,
#box.padding = unit(c(2,2,2,2), "pt")
)
get_y_pred <- function(x) ifelse(x < pi, 2/pi, -2/pi)
data_df <- data_df |> mutate(
pred_sq_err1 = (y - get_y_pred(x))^2
)
mse1 <- mean(data_df$pred_sq_err1)
mse1_str <- sprintf("%.3f", mse1)
decision_df <- tribble(
~x, ~xend, ~y, ~yend,
0, pi, 2/pi, 2/pi,
pi, 2*pi, -2/pi, -2/pi
)
reg_tree_plot +
geom_segment(
data=decision_df,
aes(x=x, xend=xend, y=y, yend=yend),
color=cbPalette[1],
linewidth = g_linewidth
) +
geom_segment(
aes(x=x, xend=x, y=get_y_pred(x), yend=y)
) +
geom_text(
aes(x=(3/2)*pi, y=0.5, label=paste0("MSE = ",mse1_str)),
size = 9,
#box.padding = unit(c(2,2,2,2), "pt")
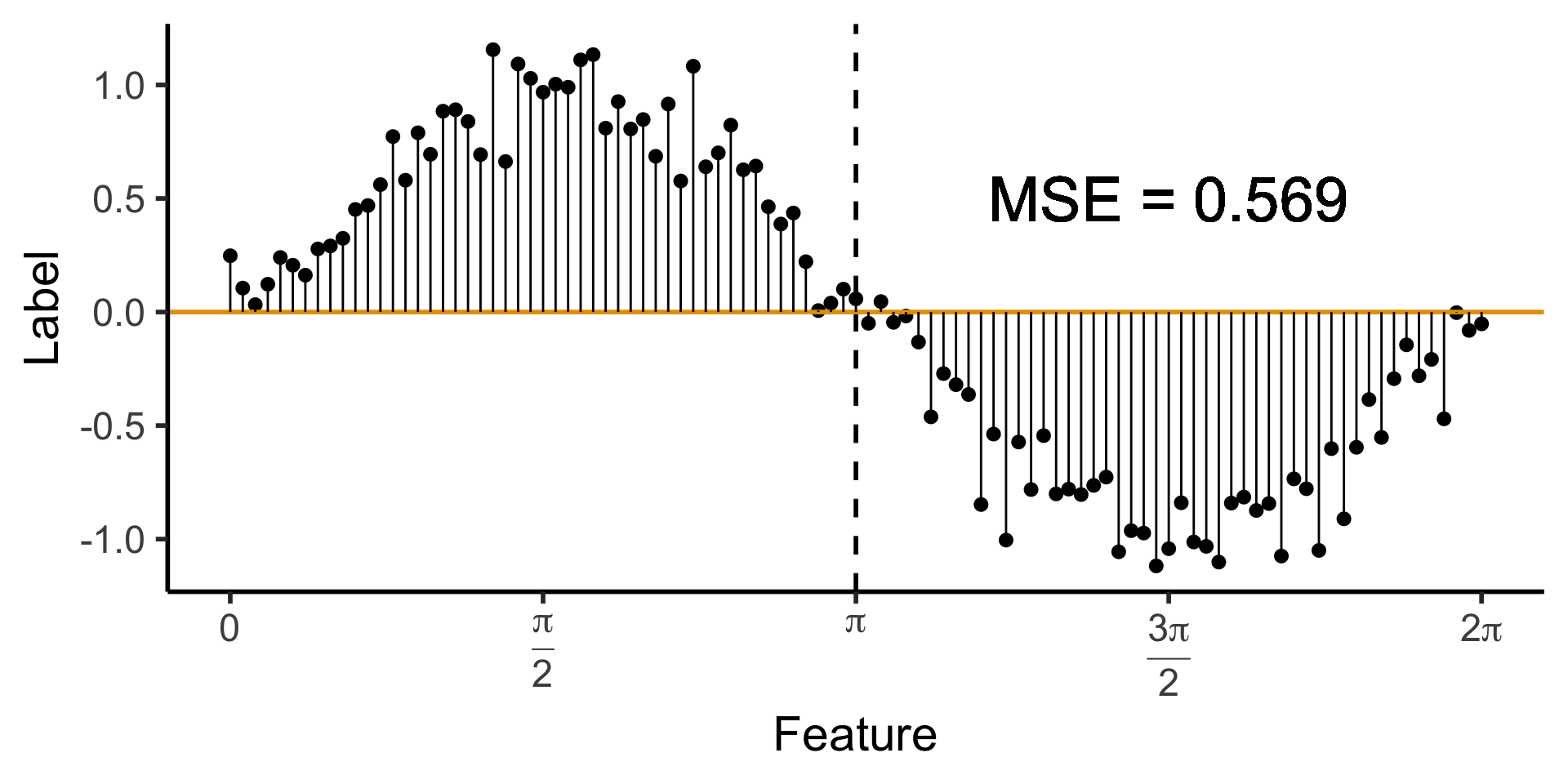
)- Original data
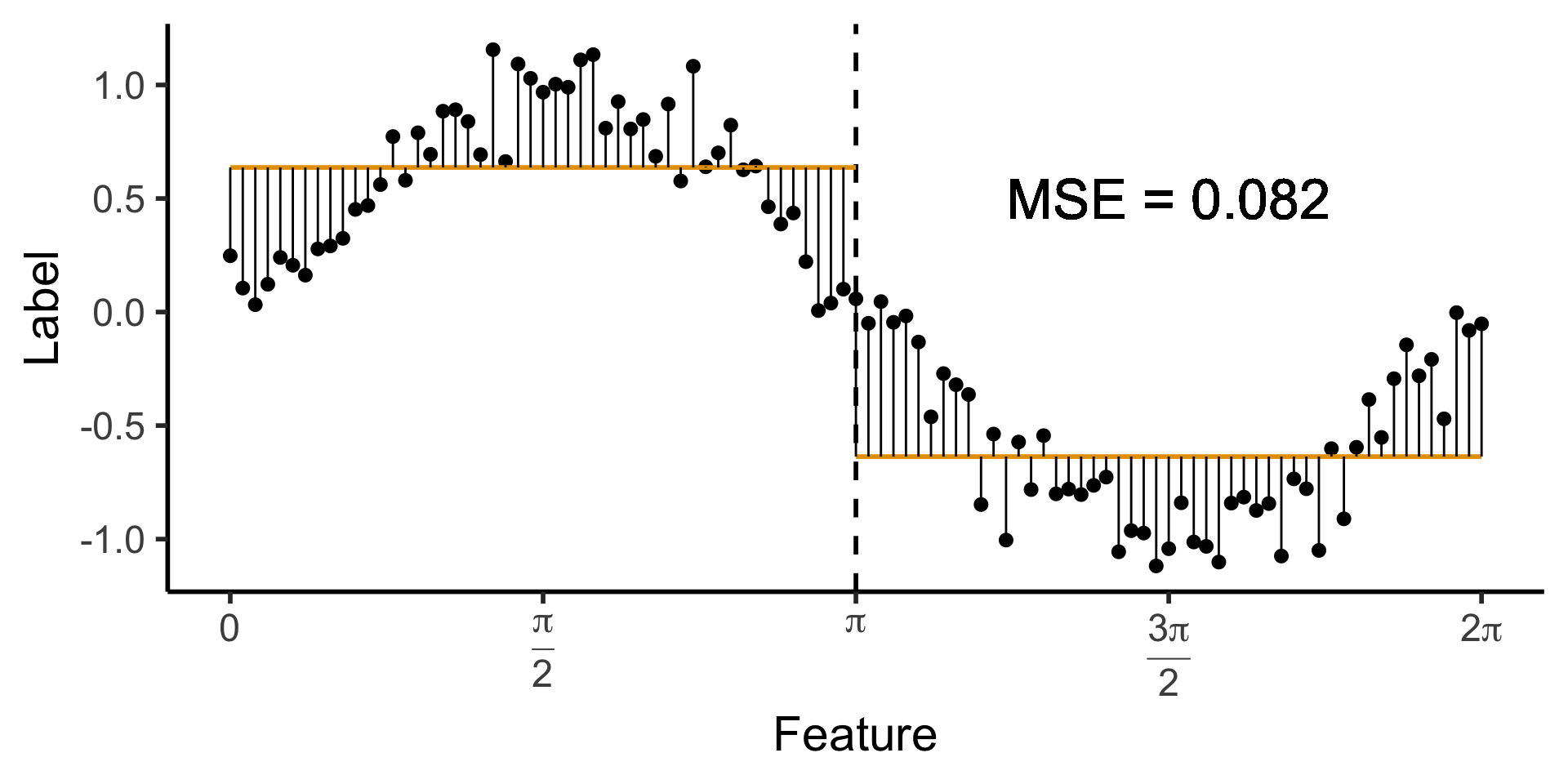
- One-level DT
Appendix: Covariance Matrix Magic
- For those interested (skipping over lots of matrix math): say you have a 2D covariance matrix \(\mathbf{\Sigma}\) with eigensystem \((\lambda_1, \mathbf{x}_1), (\lambda_2, \mathbf{x}_2)\)
- You can obtain a new covariance matrix \(\mathbf{\Sigma}'\) which has the same eigenvalues as \(\mathbf{\Sigma}\) but has eigenvectors \(\mathbf{x}'_1\) and \(\mathbf{x}'_2\), so long as these two eigenvectors are orthogonal.
- Example: you want to retain the eigenvalues \(\lambda_1 = 3\) and \(\lambda_2 = 1\) from the quiz-review slides, but want the data’s first principal component to be \(\mathbf{x}'_1 = (2,1)^\top\) and its second principal component to be \(\mathbf{x}'_2 = (-1,2)^\top\).
- By constructing the Eigenmatrix \(\mathbf{V} = \left[\begin{smallmatrix} \mathbf{x}'_1 & \mathbf{x}'_2\end{smallmatrix}\right]\) (the matrix whose columns are \(\mathbf{x}'_1\) and \(\mathbf{x}'_2\)), we can obtain \(\mathbf{\Sigma}'\) by computing:
\[ \mathbf{\Sigma}' = \mathbf{V}\mathbf{\Sigma}\mathbf{V}^{-1}. \]
- (Exercise: recreate the plot from the earlier PCA slides, but with these desired first and second principal components! See here for a deeper dive into why this works!)
References
DSAN 5000 W11: Random Forests
 , and the effect goes away (biases no longer cancel out)
, and the effect goes away (biases no longer cancel out)