Week 11: From Serial to Parallel Pipelines

DSAN 5500: Data Structures, Objects, and Algorithms in Python

Author

Affiliation

Jeff Jacobs

jj1088@georgetown.edu

Open slides in new window →

Schedule

Today’s Planned Schedule:

	Start	End	Topic
Lecture	6:30pm	7:30pm	[Embarrassingly] Parallel Pipelines →
	7:30pm	8:00pm	Beyond Embarrassingly Parallel →
Break!	8:00pm	8:10pm
	8:10pm	9:00pm	Data Mining in Parallel →

Serial Pipelines \(\rightarrow\) Parallel Pipelines

• Don’t worry; for now, just a high-level overview of what we’ll dive into in the final unit

Quick Survey Question, for Intuition-Building

• Are humans capable of “true” multi-tasking?
  • As in, doing two things at the exact same time?
• (Or, do we instead rapidly switch back and forth between tasks?)

The Answer

• (From what we understand, at the moment, by way of studies in neuroscience/cognitive science/etc…)
• Humans are not capable of true multitasking! In CS terms, this would be called multiprocessing (more on this later)
• We are capable, however, of various modes of concurrency!

	Multithreading	Asynchronous Execution
Unconsciously (you do it already, “naturally”)	Focus on one speaker within a loud room, with tons of other conversations entering your ears	Put something in oven, set alarm, go do something else, take out of oven once alarm goes off
Consciously (you can do it with effort/practice)	Pat head (up and down) and rub stomach (circular motion) “simultaneously”	Throw a ball in the air, clap 3 times, catch ball

Helpful Specifically for Programming

• Course notes from MIT’s class on parallel computing phrases it like: if implemented thoughtfully, concurrency is a power multiplier for your code (do 10 things in 1 second instead of 10 seconds…)

Helpful In General as a Way of Thinking!

• Say you get hired as a Project Manager…
• Part of your job will fundamentally involve pipelines!
  • Need to know when Task \(B\) does/does not require Task \(A\) as a prerequisite
  • Need to know whether Task \(A\) and Task \(B\) can share one resource or need their own individual resources
  • Once Task \(A\) and \(B\) both complete, how do we merge their results together?

Avoiding the Rabbithole

• Parallel computing is a rabbithole, but one you can safely avoid via simple heuristics (“rules of thumb”)!

1. Check for optimizations to serial code first,
2. Check for embarrassingly parallel code blocks
3. Use map-reduce approach for more complicated cases

“Embarrassingly Parallel” Pipelines

• Technical definition: tasks within pipeline can easily be parallelized bc no dependence and no need for communication (see next slide). Better video explanation:

Parallelizing Non-Embarrassingly-Parallel Pipelines

epic_bacon_lifehack.jpeg

Buzzkill: Complications to Come 😰

• If it’s such a magical powerup, shouldn’t we just parallelize everything? Answer: No 😞 because overhead.
• Overhead source 1: Beyond “embarrassingly parallel” cases, threads may require their own separate stacks and heaps
• Overhead source 2: Even after setting up new stacks and heaps, threads may need to communicate with each other (e.g. if they need to synchronize at some point(s))
• In fact, probably the earliest super-popular parallelization library was created to handle Source 2, not Source 1: Message Passing Interface (C, C++, and Fortran)

The Worst Part, IMO

• Plenty of problems in CS/data science have these kinds of complications… (if they weren’t complicated, we wouldn’t have as many jobs)
• We saw for example, with hash tables, how we can work to minimize collisions (MD5 and other provably-optimal hash functions), but can’t eliminate them entirely
  • So, we tackle this complication by also developing efficient collision-handling structures like BSTs!
• With parallel overhead costs, however… I don’t know of any easily-accessible “thing” like the theory of hash tables that can be used to optimize parallelization
  • In other words, you would think we could do a similar optimization: paralellize if benefits > costs, keep as serial otherwise
  • But, if you try to find a “framework” for this, you’ll mostly find StackOverflow posts, textbooks, etc. which say “stuff varies too much between different chipsets, languages, operating systems, etc… sorry!”

The Solution?

• Again, as far as I can tell (despite workshops/courses and two summer internships just parallelizing stuff)…
• You just start trying to parallelize, carefully measure and test the performance gains/losses, and then
• Decide whether to commit to parallel or stick to serial, via an estimate of how your analysis/app will need to scale!
• Hence the usefulness of Prefect for visualizing tradeoff:
  • Tasks which used to run in serial will now run at same time, but will take longer (unless embarrassingly parallel) due to setup+communication overhead

In Action

import time
from sympy.ntheory import factorint
from joblib import Parallel, delayed
parallel_runner = Parallel(n_jobs=4)
start, end = 500, 580
def find_prime_factors(num):
  time.sleep(.01)
  return factorint(num, multiple=True)
disp_time = lambda start, end: print('{:.4f} s'.format(end - start))

serial_start = time.time()
result = [
  (i,find_prime_factors(i))
  for i in range(start, end+1)
]
serial_end = time.time()
disp_time(serial_start, serial_end)

0.9668 s

par_start = time.time()
result = parallel_runner(
  delayed(find_prime_factors)(i)
  for i in range(start, end+1)
)
par_end = time.time()
disp_time(par_start, par_end)

2.7822 s

Beyond Embarrassingly Parallel Tasks…

What Happens When Not Embarrassingly Parallel?

• Think of the difference between linear and quadratic equations in algebra:
• \(3x - 1 = 0\) is “embarrassingly” solvable, on its own: you can solve it directly, by adding 3 to both sides \(\implies x = \frac{1}{3}\). Same for \(2x + 3 = 0 \implies x = -\frac{3}{2}\)
• Now consider \(6x^2 + 7x - 3 = 0\): Harder to solve “directly”, so your instinct might be to turn to the laborious quadratic equation:

\[ \begin{align*} x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} = \frac{-7 \pm \sqrt{49 - 4(6)(-3)}}{2(6)} = \frac{-7 \pm 11}{12} = \left\{\frac{1}{3},-\frac{3}{2}\right\} \end{align*} \]

• And yet, \(6x^2 + 7x - 3 = (3x - 1)(2x + 3)\), meaning that we could have split the problem into two “embarrassingly” solvable pieces, then multiplied to get result!

The Analogy to Map-Reduce

\(\leadsto\) If code is not embarrassingly parallel (instinctually requiring laborious serial execution),	\(\underbrace{6x^2 + 7x - 3 = 0}_{\text{Solve using Quadratic Eqn}}\)
But can be split into…	\((3x - 1)(2x + 3) = 0\)
Embarrassingly parallel pieces which combine to same result,	\(\underbrace{3x - 1 = 0}_{\text{Solve directly}}, \underbrace{2x + 3 = 0}_{\text{Solve directly}}\)
We can use map-reduce to achieve ultra speedup (running “pieces” on GPU!)	\(\underbrace{(3x-1)(2x+3) = 0}_{\text{Solutions satisfy this product}}\)

The Direct Analogy: Map-Reduce!

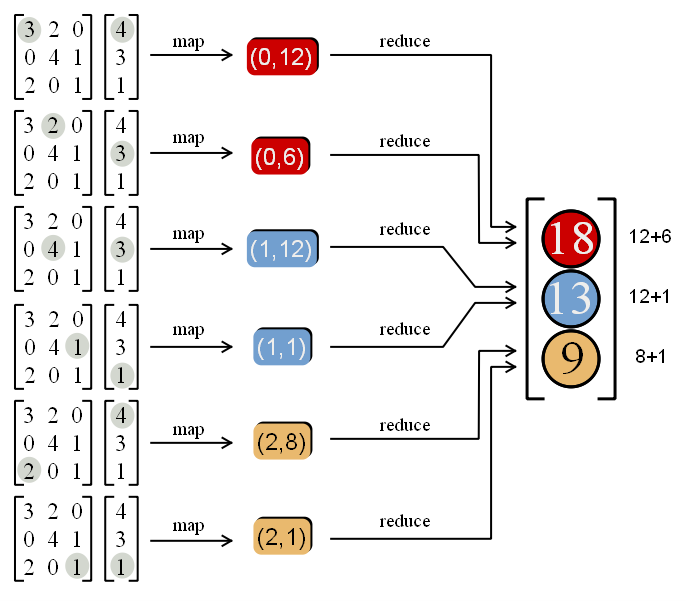
• Problem from DSAN 5000/5100: Computing SSR (Sum of Squared Residuals)
• \(y = (1,3,2), \widehat{y} = (2, 5, 0) \implies \text{SSR} = (1-2)^2 + (3-5)^2 + (2-0)^2 = 9\)
• Computing pieces separately:

map(do_something_with_piece, list_of_pieces)

my_map = map(lambda input: input**2, [(1-2), (3-5), (2-0)])
map_result = list(my_map)
map_result

[1, 4, 4]

• Combining solved pieces

reduce(how_to_combine_pair_of_pieces, pieces_to_combine)

from functools import reduce
my_reduce = reduce(lambda piece1, piece2: piece1 + piece2, map_result)
my_reduce

9

Functional Programming (FP)

Functions vs. Functionals

• You may have noticed: map() and reduce() are “meta-functions”: functions that take other functions as inputs

def add_5(num):
  return num + 5
add_5(10)

15

def apply_twice(fn, arg):
  return fn(fn(arg))
apply_twice(add_5, 10)

20

• In Python, functions can be used as vars (Hence lambda):

add_5 = lambda num: num + 5
apply_twice(add_5, 10)

20

• This relates to a whole paradigm, “functional programming”: mostly outside scope of course, but lots of important+useful takeaways/rules-of-thumb! →

Train Your Brain for Functional Approach \(\implies\) Master Debugging!

• In CS Theory: enables formal proofs of correctness
• In CS practice:

When a program doesn’t work, each function is an interface point where you can check that the data are correct. You can look at the intermediate inputs and outputs to quickly isolate the function that’s responsible for a bug.
(from Python’s “Functional Programming HowTo”)

Code \(\rightarrow\) Pipelines \(\rightarrow\) Debuggable Pipelines

• Scenario: Run code, check the output, and… it’s wrong 😵 what do you do?
• Usual approach: Read lines one-by-one, figuring out what they do, seeing if something pops out that seems wrong; adding comments like # Convert to lowercase

• Easy case: found typo in punctuation removal code. Fix the error, add comment like # Remove punctuation

  Rule 1 of FP: transform these comments into function names

• Hard case: Something in load_text() modifies a variable that later on breaks remove_punct() (Called a side-effect)

  Rule 2 of FP: NO SIDE-EFFECTS!

(Does this way of diagramming a program look familiar?)

• With side effects: ❌ \(\implies\) issue is somewhere earlier in the chain 😩🏃‍♂️
• No side effects: ❌ \(\implies\) issue must be in remove_punct()!!! 😎 ⏱️ = 💰

If It’s So Useful, Why Doesn’t Everyone Do It?

• Trapped in imperative (sequential) coding mindset: Path dependency / QWERTY
• Reason we need to start thinking like this is: it’s 1000x harder to debug parallel code! So we need to be less ad hoc in how we write+debug, from here on out! 🙇‍♂️🙏

From Leskovec, Rajaraman, and Ullman (2014)

The title relates to a classic Economics joke (the best kind of joke): “An economist and a CEO are walking down the street, when the CEO points at the ground and tells the economist, ‘look! A $20 bill on the ground!’ The economist keeps on walking, scoffing at the CEO: ‘don’t be silly, if there was a $20 bill on the ground, somebody would have picked it up already’.”

But… Why is All This Weird Mapping and Reducing Necessary?

• Without knowing a bit more of the internals of computing efficiency, it may seem like a huge cost in terms of overly-complicated overhead, not to mention learning curve…

The “Killer Application”: Matrix Multiplication

• (I learned from Jeff Ullman, who did the obnoxious Stanford thing of mentioning in passing how “two previous students in the class did this for a cool final project on web crawling and, well, it escalated quickly”, aka became Google)

From Leskovec, Rajaraman, and Ullman (2014), which is (legally) free online!

The Killer Way-To-Learn: Text Counts!

• (2014): Text counts (2.2) \(\rightarrow\) Matrix multiplication (2.3) \(\rightarrow \cdots \rightarrow\) PageRank (5.1)
• (And yall thought it was just busywork for HW3 😏)
• The goal: User searches “Denzel Curry”… How relevant is a given webpage?
• Scenario 1: Entire internet fits on CPU \(\implies\) We can just make a big big hash table:

If Everything Doesn’t Fit on CPU…

From Cornell Virtual Workshop, “Understanding GPU Architecture”

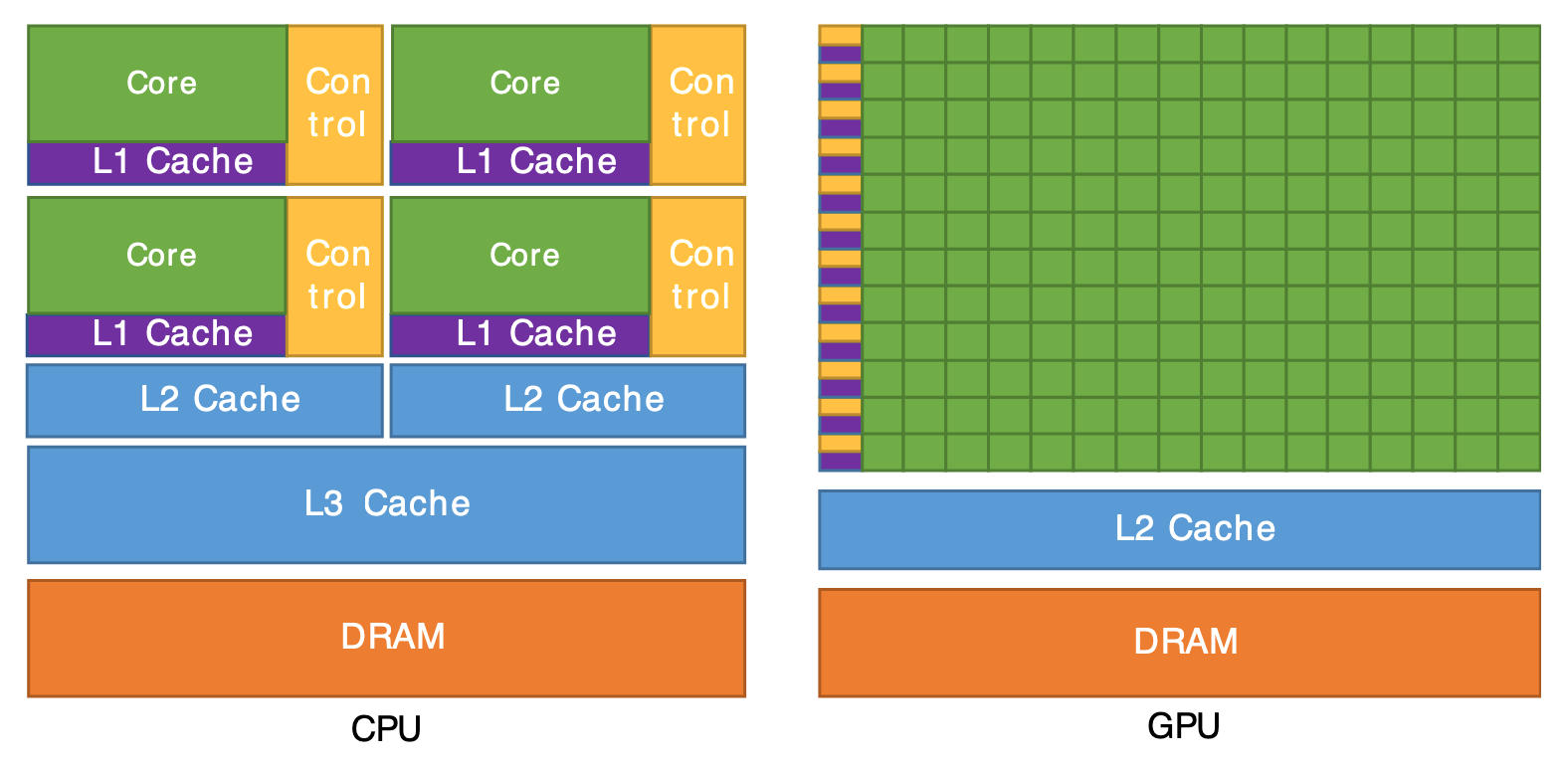
Break Problem into Chunks for the Green Bois!

• \(\implies\) Total = \(O(3n) = O(n)\)
• But also optimized in terms of constants, because of sequential memory reads

HW5: Possibility 1

• Map-Reduced Matrix-Vector Multiplication

Image source

HW5: Possibility 2 (More Likely?)

• Scrape quotes in parallel!
• Advantage: Builds on HW4
• Disadvantage: Embarrassingly parallel, so… no Map-Reduce coding practice
• (Probable tiebreaker: If you’re interested in Map-Reduce, do Matrix Multiplication as Final Project!)

References

Leskovec, Jure, Anand Rajaraman, and Jeffrey David Ullman. 2014. Mining of Massive Datasets. Cambridge University Press.