PPOL 6805 / DSAN 6750: GIS for Spatial Data Science
Fall 2025
source("../dsan-globals/_globals.r")
set.seed(6805)
library(tidyverse) |> suppressPackageStartupMessages()
library(sf) |> suppressPackageStartupMessages()
library(spatstat) |> suppressPackageStartupMessages()
library(mdthemes) |> suppressPackageStartupMessages()
library(mapview) |> suppressPackageStartupMessages()
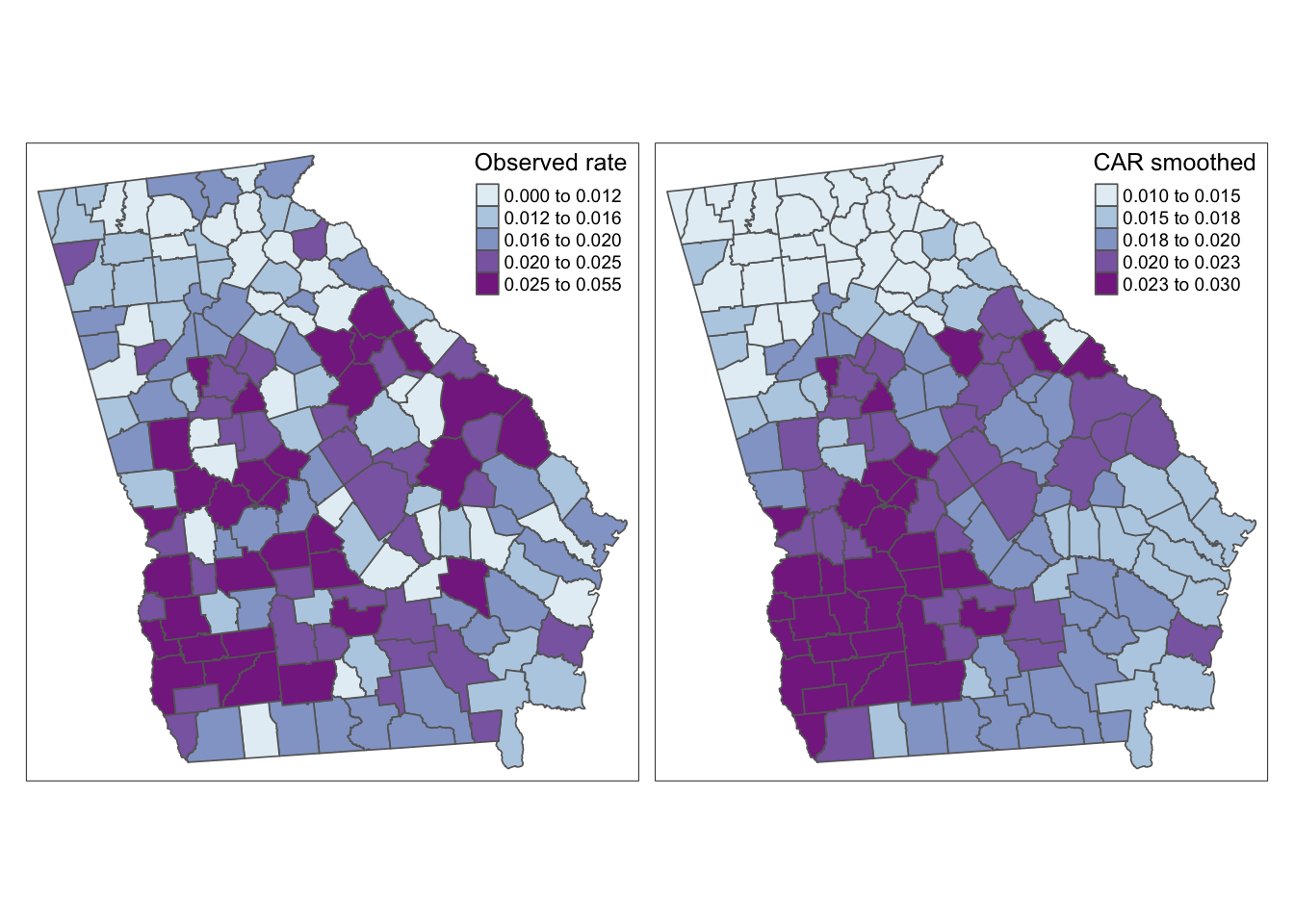
library(leaflet) |> suppressPackageStartupMessages()library(mapview) |> suppressPackageStartupMessages()
city_df <- tibble::tribble(
~city, ~lon, ~lat, ~pop,
"Chicago", 41.950567516553896, -87.93011127491978, 2746388,
"Detroit", 42.45123004999075, -83.18402319217698, 631524
)
city_sf <- sf::st_as_sf(
city_df,
coords = c("lat", "lon"),
crs=4326
)
city_buf_sf <- city_sf |> sf::st_buffer(20000)
city_cases_sf <- city_buf_sf |> sf::st_sample(size=rep(10,2)) |> sf::st_as_sf()
city_cases_sf$city <- "Detroit (10 Cases)"
city_cases_sf[1:10, 'city'] <- "Chicago (10 Cases)"
city_cases_sf$sample <- "Flu"
mapview(city_cases_sf, zcol="city")| Chicago | Detroit | |
|---|---|---|
| Population | 2,746,388 | 631,524 |
library(leaflet) |> suppressPackageStartupMessages()
library(leaflet.extras2) |> suppressPackageStartupMessages()
city_pop_sf <- city_buf_sf |> sf::st_sample(size=c(16, 4)) |> sf::st_as_sf()
city_pop_sf$city <- "Detroit"
city_pop_sf[1:16, 'city'] <- "Chicago"
city_pop_sf$sample <- "People"
city_combined_sf <- bind_rows(city_cases_sf, city_pop_sf)
# mapview(city_combined_sf, zcol="city", marker="sample")
Flu = makeIcon(
"https://upload.wikimedia.org/wikipedia/commons/thumb/c/c3/Maki2-danger-24.svg/240px-Maki2-danger-24.svg.png",
"https://upload.wikimedia.org/wikipedia/commons/thumb/c/c3/Maki2-danger-24.svg/24px-Maki2-danger-24.svg.png",
20,
20
)
People = makeIcon(
"https://upload.wikimedia.org/wikipedia/commons/thumb/e/ef/Maki2-pitch-24.svg/24px-Maki2-pitch-24.svg.png",
"https://upload.wikimedia.org/wikipedia/commons/thumb/e/ef/Maki2-pitch-24.svg/24px-Maki2-pitch-24.svg.png",
20,
20
)
city_combined_sf$r <- ifelse(city_combined_sf$sample == "Flu", 0, 4)
city_flu_sf <- city_combined_sf |> filter(sample == "Flu")
city_ppl_sf <- city_combined_sf |> filter(sample == "People")
leaflet(city_flu_sf) |>
addProviderTiles("CartoDB.Positron") |>
addMarkers(data=city_flu_sf, icon = Flu) |>
addMarkers(data=city_ppl_sf, icon = People)Cases of disease form an intensity function \(\lambda(\mathbf{s})\)
Controls form an “ambient” intensity function \(\lambda_0(\mathbf{s})\)
\(\implies\) The following model allows us to separate the quantities we really care about from the base rate information:
\[ \lambda(\mathbf{s}) = \alpha \overbrace{\lambda_0(\mathbf{s})}^{\mathclap{\text{Base Rate}}} \underbrace{\rho(\mathbf{s})}_{\mathclap{\text{Relative Risk}}}, \]
where
\[ \alpha = \frac{\# \text{Cases}}{\# \text{Controls}} \]
(Remember: unit of \(\lambda(\mathbf{s})\) is number of cases; not a probability density!)
library(sparr) |> suppressPackageStartupMessages()
data(pbc)
controls <- unmark(pbc[which(pbc$marks == "control"), ])
controls |> sf::st_as_sf() |> ggplot() +
geom_sf() +
theme_classic() +
labs(title="Controls (Population Sample)")
cases <- unmark(pbc[which(pbc$marks == "case"), ])
cases |> sf::st_as_sf() |> ggplot() +
geom_sf() +
theme_classic() +
labs(title="PBC Cases")
density() from spatstat makes “smart” choices for this bandwidth, so for now we just average the bandwidths estimated for cases and controls:library(sparr)
data(pbc)
cases <- unmark(pbc[which(pbc$marks == "case"), ])
controls <- unmark(pbc[which(pbc$marks == "control"), ])
bwcases <- attr(density(cases), "sigma")
bwcontr <- attr(density(controls), "sigma")
(bw <- (bwcases + bwcontr)/2)[1] 11.45837int_controls <- density(controls, sigma = bw, eps=0.25)
plot(int_controls, main = "Control Intensity")
int_cases <- density(cases, sigma = bw, eps=0.25)
plot(int_cases, main = "Case Intensity")
library(fields)
(alpha_hat <- cases$n/controls$n)[1] 0.2519868x <- int_cases$xcol
y <- int_cases$yrow
rr <- t(int_cases$v)/t(alpha_hat * int_controls$v)
image.plot(x, y, rr, asp = 1)
title(xlab = "Easting", ylab = "Northing")
HHHHHTHHHH…H, or could be fair (lots of heads by chance!)
plot_rlabel <- function(rl_ppp) {
rl_win_sf <- window_to_sf(rl_ppp)
rl_points_sf <- points_to_sf(rl_ppp) |>
rename(
type = spatstat.geom..marks.x.
)
rl_plot <- ggplot() +
geom_sf(
data=rl_win_sf,
alpha=0.3
) +
geom_sf(
mapping=aes(fill=type, alpha=type),
data=rl_points_sf,
size=2,
# alpha=0.75,
shape=21,
stroke=0.1,
# color='white',
) +
# scale_color_manual(
# "Point Type",
# values=c("control"="gray","case"=cb_palette[1])
# ) +
scale_fill_manual(
"Type",
values=c("control"="gray","case"=cb_palette[1])
) +
scale_alpha_manual(
"Type",
values=c("control"=0.5, "case"=1.0)
) +
theme_classic(base_size=16) +
labs(
title="NE Britain Disease Cases"
)
return(rl_plot)
}
set.seed(6810)
rl1_ppp <- rlabel(pbc)
plot_rlabel(rl1_ppp)
set.seed(6811)
pbc_2 <- rlabel(pbc)
plot_rlabel(pbc_2)
set.seed(6812)
pbc_3 <- rlabel(pbc)
plot_rlabel(pbc_3)
pbc_win_sf <- pbc |> sf::st_as_sf() |> filter(label == "window")
plot_pbc_sim <- function() {
pbc_sim <- spatstat.random::rpoispp(
lambda = alpha_hat * int_controls
)
# Separate window and points
pbc_sf <- pbc_sim |> sf::st_as_sf()
pbc_point_sf <- pbc_sf |> filter(label == "point")
pbc_win_sf <- pbc_sf |> filter(label == "window")
pbc_plot <- ggplot() +
geom_sf(data=pbc_win_sf) +
geom_sf(data=pbc_point_sf, size=0.5, alpha=0.5) +
theme_classic()
return(pbc_plot)
}
plot_pbc_sim()
plot_pbc_sim()
plot_pbc_sim()
spdep
\[ Y_i = \beta_0 + \beta_1X_{i,1} + \beta_2X_{i,2} + \cdots + \beta_MX_{i,M} + \varepsilon_i \]
Importance of OLS regression: can give us the Best Linear Unbiased Estimator (BLUE)
This is only true if the Gauss-Markov assumptions hold—one of these is that the error terms are uncorrelated:
\[ \text{Cov}[\varepsilon_i, \varepsilon_j] = 0 \; \forall i \neq j \]
| \(N = 477\) | \(\widehat{\beta}\) | SE | \(t\) |
|---|---|---|---|
| Intercept | 35.30 | 2.21 | 15.96 |
| Log GDP per cap | 13.46 | 0.65 | 20.84 |
Moran’s \(I\) for residuals = 0.47(!)
| \(N = 477\) | \(\widehat{\beta}\) | SE | \(t\) |
|---|---|---|---|
| Intercept | 4.70 | 1.66 | 2.80 |
| Log GDP per cap | 1.77 | 0.48 | 3.66 |
| \(\rho\) | 0.87 | 0.02 | 36.7 |
\[ Y_i = \underbrace{\mu_i}_{\text{Non-spatial model}} + \underbrace{\frac{1}{w_{i,cdot}}\sum_{j \neq i}(Y_j - \mu_j)}_{\text{Spatial Autocorrelation}} + \varepsilon_i \]
\[ Y = \mathbf{X}\beta + \rho \underbrace{\mathbf{W}Y}_{\mathclap{\text{Spatially-lagged }Y}} + \boldsymbol\varepsilon \]
