Birthdays as Instruments for Catholic School Effects

Labs
Published

July 20, 2025

Overview

In this writeup, the goal is to walk through a third approach (in addition to adjusting for covariates and propensity score weighting) you can take towards tackling the issue of confounding. The following diagram illustrates what we’re hoping to achieve:

  • We want to estimate the (average) causal effect of Catholic Schooling \(D\) on Post-Grad Earnings \(Y\).
  • However, there is an unmeasured covariate, Work Ethic \(X\) (a fork relative to \(D \leftarrow X \rightarrow Y\)), which is confounding this effect \(D \rightarrow Y\).
  • So, as Angrist and Krueger (1991) proposed, we can “work around” this confounding (literally, given how the diagram is set up) by using day of birth relative to school cohort as an instrument:
    • Since this day of birth has no direct causal relationship with work ethic, and
    • Has no direct causal relationship with Post-Grad Earnings (only an indirect effect on it through Catholic Schooling \(D\)),
    • This cohort-relative date of birth can play the same role that a random coin flip plays in the “gold standard” of randomized medical trials!
  • Under these assumptions (which need to be argued for! And are argued for in Angrist and Krueger (1991)), we can recover the causal effect of \(D\) on \(Y\) via the “classical IV estimator”:

\[ \beta_{\text{IV}}^{D \rightarrow Y} = \frac{\text{Cov}[Z,Y]}{\text{Cov}[D,Y]} \]

Causal diagram illustrating the role of our proposed instrument \(Z\): a student’s day of birth within the cohort they enter school with. If \(Z\) has (a) no direct causal relationship with Work Ethic (\(X\)) and (b) no direct causal relationship with Post-Grad Earnings \(Y\) (that is, only an indirect effect on it through Catholic Schooling \(D\)), then we can recover the causal effect of Catholic Schooling on Post-Grad Earnings by computing \(\beta_{\text{IV}}^{D \rightarrow Y} = \frac{\text{Cov}[Z,Y]}{\text{Cov}[D,Y]}\)

In this writeup, we will generate simulated data on birthdates, school-dropout behavior, and eventual earnings, then use the above IV estimator formula to recover the causal effect of Catholic Schooling on Post-Grad Earnings. We can then verify the accuracy of this estimate, since we generated the data in the first place! The beauty of generative modeling 😉

Uniformly-Distributed Birthdays and Catholic Schooling

Code 
library(tidyverse) |> suppressPackageStartupMessages()
library(lubridate) |> suppressPackageStartupMessages()
library(extraDistr) |> suppressPackageStartupMessages()
library(scales) |> suppressPackageStartupMessages()
set.seed(5650)
n <- 10000
dob_vals <- lubridate::make_date(1999, 8, 27)
cath_vals <- rbern(n, prob=0.5)
offset_vals <- rdunif(n, min=0, max=364)
student_df <- tibble(day_of_yr=offset_vals, catholic=factor(cath_vals)) |>
  mutate(
    dob=dob_vals + duration(day_of_yr, unit="days") - duration(1, unit="days"),
    turns_18 = lubridate::as_date(dob + duration(18, unit="years"))
  ) |>
  arrange(dob)
#duration(sample(0:364, n()), unit = "days"))
student_df <- student_df |> mutate(
  year_abbr = as.character(lubridate::year(dob)),
  month_str = factor(
    paste0("",month.abb[lubridate::month(dob)],"",str_sub(year_abbr, 3, 4)),
    levels=c(
      "Aug99","Sep99","Oct99","Nov99","Dec99","Jan00","Feb00",
      "Mar00","Apr00","May00","Jun00","Jul00","Aug00"
    )
  )
)
student_df |> head()
day_of_yr catholic dob turns_18 year_abbr month_str
0 0 1999-08-26 2017-08-25 1999 Aug99
0 0 1999-08-26 2017-08-25 1999 Aug99
0 1 1999-08-26 2017-08-25 1999 Aug99
0 1 1999-08-26 2017-08-25 1999 Aug99
0 0 1999-08-26 2017-08-25 1999 Aug99
0 0 1999-08-26 2017-08-25 1999 Aug99

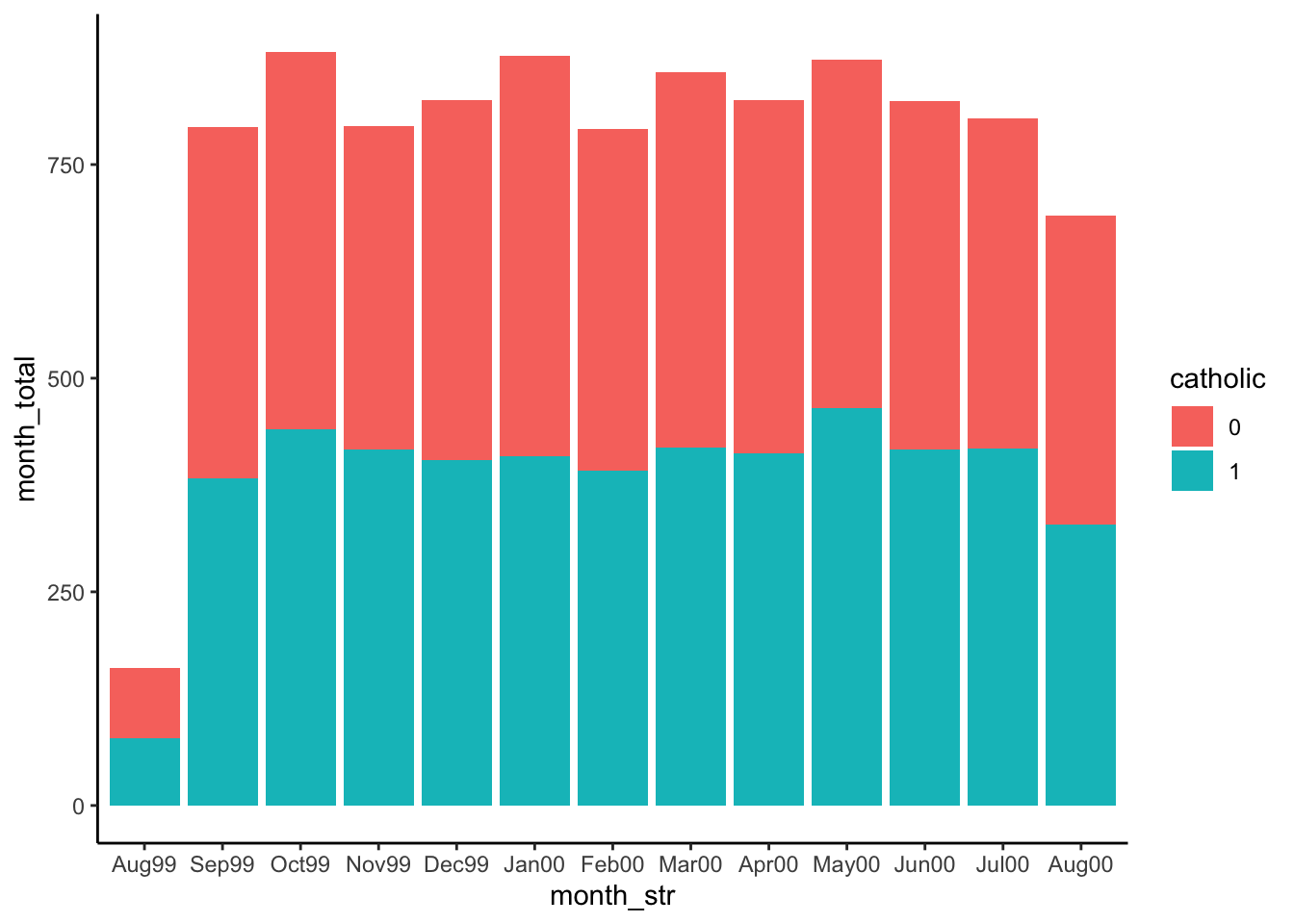
Number of Students Per Month

Code 
month_df <- student_df |> group_by(month_str, catholic) |> summarize(month_total=n())
month_df |> ggplot(aes(x=month_str,y=month_total, fill=catholic)) +
  geom_bar(stat='identity') +
  theme_classic()

Now the Dropping-Out Simulation

  • First day of school year: Aug 26
  • Last day of school: Jun 18
  • \(\implies\) This cohort = all who turn 5 yrs old between Aug 27 2004 and Aug 26 2005
  • \(\implies\) All born between Aug 27 1999 and Aug 26 2000
Code 
student_df <- student_df |> mutate(
  can_drop_out = as.numeric(turns_18 <= lubridate::make_date(2018, 6, 18))
)
student_df |> group_by(dob) |> summarize(sum(can_drop_out)) |> head()
dob sum(can_drop_out)
1999-08-26 25
1999-08-27 30
1999-08-28 30
1999-08-29 29
1999-08-30 23
1999-08-31 24

What percentage of students will actually have a chance to drop out? i.e., What proportion of students are born so that they turn 18 before the last day of school?

Code 
(elig_prop <- student_df |> summarize(elig_prop=mean(can_drop_out)) |> pull())
[1] 0.8174
Code 
# National mean 8.6%
raw_dropout_rate <- 0.086
(dropout_rate <- (1/elig_prop) * raw_dropout_rate)
[1] 0.1052116
Code 
# Simulate desire to drop out
set.seed(5651)
wtd_vals <- rbern(nrow(student_df), prob=dropout_rate)
student_df$wants_to_drop <- wtd_vals
student_df <- student_df |> mutate(
  dropout = as.numeric(wants_to_drop==1 & can_drop_out==1)
)
mean(student_df$dropout)
[1] 0.0846
Code 
student_df |> group_by(turns_18) |> summarize(
  dob_dropouts=sum(dropout),
  wants_dropout=sum(wants_to_drop),
  total=n(), 
) |> head()
turns_18 dob_dropouts wants_dropout total
2017-08-25 1 1 25
2017-08-26 5 5 30
2017-08-27 7 7 30
2017-08-28 3 3 29
2017-08-29 1 1 23
2017-08-30 3 3 24

Compute Cumulative Number of Dropouts Over Time

Code 
dob_df <- student_df |> group_by(dob, catholic) |> summarize(
  dob_dropout=sum(dropout)
)
`summarise()` has grouped output by 'dob'. You can override using the `.groups`
argument.
Code 
#dob_df$drop_todate <- cumsum(dob_df$dob_dropout)
#dob_df |> group_by(catholic) |> summarize(drop_todate=cumsum(dob_dropout)) |> ungroup()
dob_df <- dob_df |> group_by(catholic) |> arrange(dob) |>
  mutate(drop_todate=cumsum(dob_dropout)) |>
  ungroup()

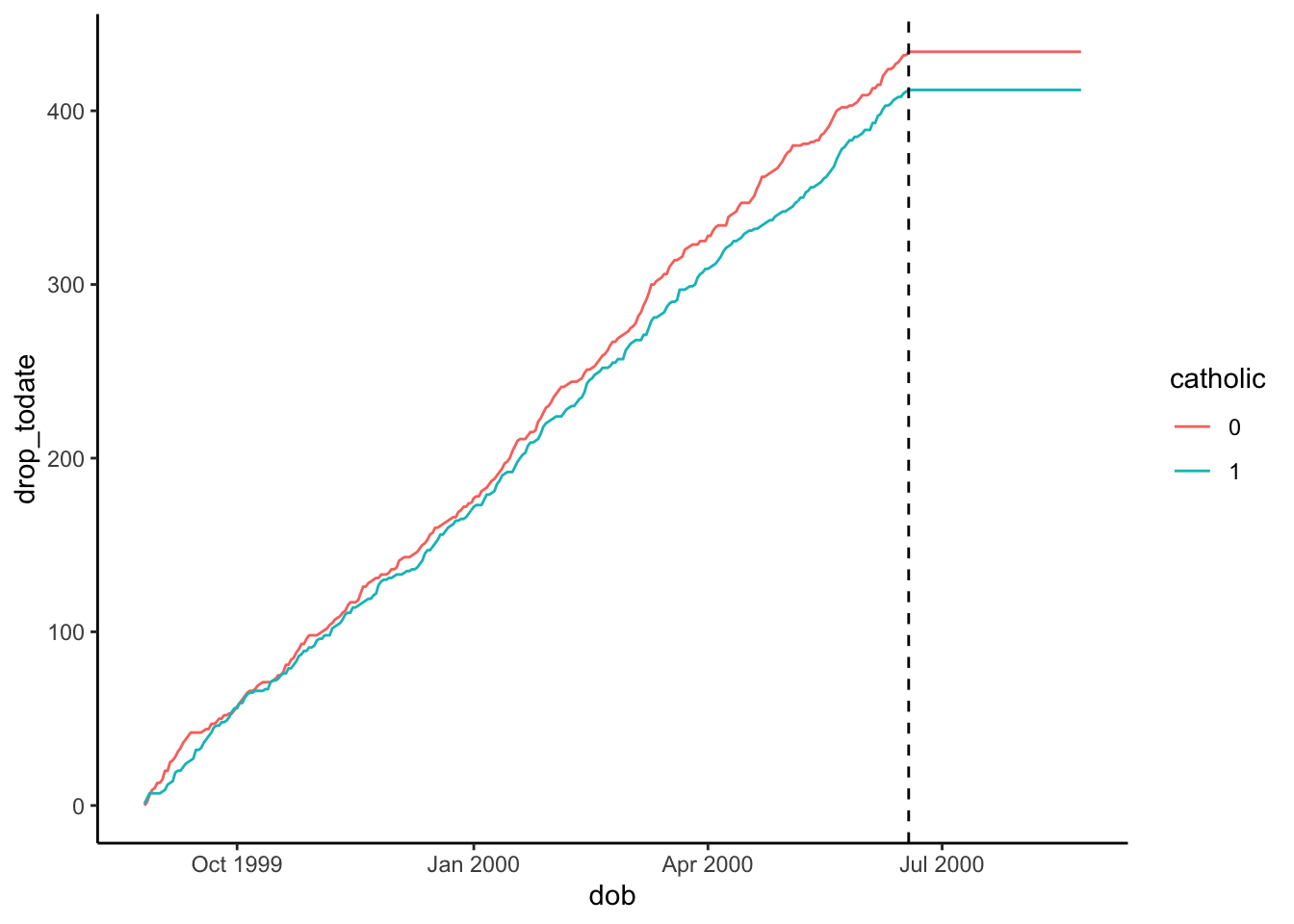
Plot Cumulative Dropouts by Day

Code 
dob_df |> ggplot(aes(x=dob, y=drop_todate, color=catholic)) +
  geom_line(linewidth=0.5) +
  geom_vline(
    xintercept=lubridate::make_date(2000, 6, 18),
    linetype='dashed',
  ) +
  theme_classic()

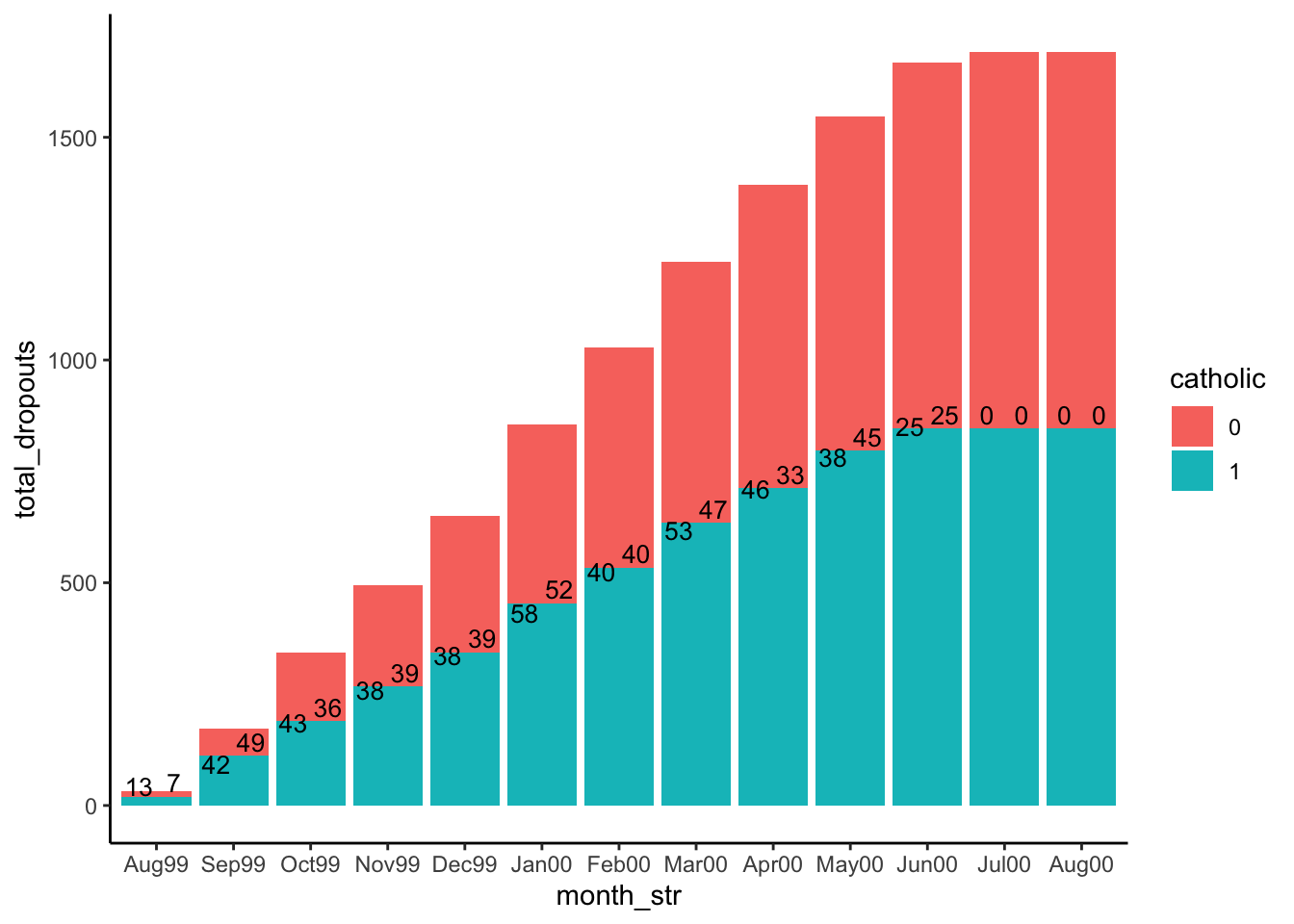
Plot Cumulative Dropouts by Month

Code 
dob_df <- dob_df |> mutate(
  year_abbr = as.character(lubridate::year(dob)),
  month_str = factor(
    paste0("",month.abb[lubridate::month(dob)],"",str_sub(year_abbr, 3, 4)),
    levels=c(
      "Aug99","Sep99","Oct99","Nov99","Dec99","Jan00","Feb00",
      "Mar00","Apr00","May00","Jun00","Jul00","Aug00"
    )
  )
)
month_drop_df <- dob_df |> group_by(month_str, catholic) |>
  summarize(month_dropout=sum(dob_dropout))
`summarise()` has grouped output by 'month_str'. You can override using the
`.groups` argument.
Code 
month_drop_df$total_dropouts <- cumsum(month_drop_df$month_dropout)
month_drop_df <- month_drop_df |> mutate(
  next_month = lead(month_str, default="Aug00"),
  prev_month_dropouts = lag(total_dropouts, default=0),
  change = total_dropouts - prev_month_dropouts
)
# month_drop_df
month_drop_df |> ggplot(aes(x=month_str, y=total_dropouts, fill=catholic)) +
  geom_bar(stat='identity') +
  # geom_segment(aes(xend=next_month), linetype="dashed") +
  geom_text(
    aes(label=month_dropout),
    position=position_dodge(width=0.9),
    vjust=-0.25, size=3.5, show.legend=FALSE
  ) +
  theme_classic()

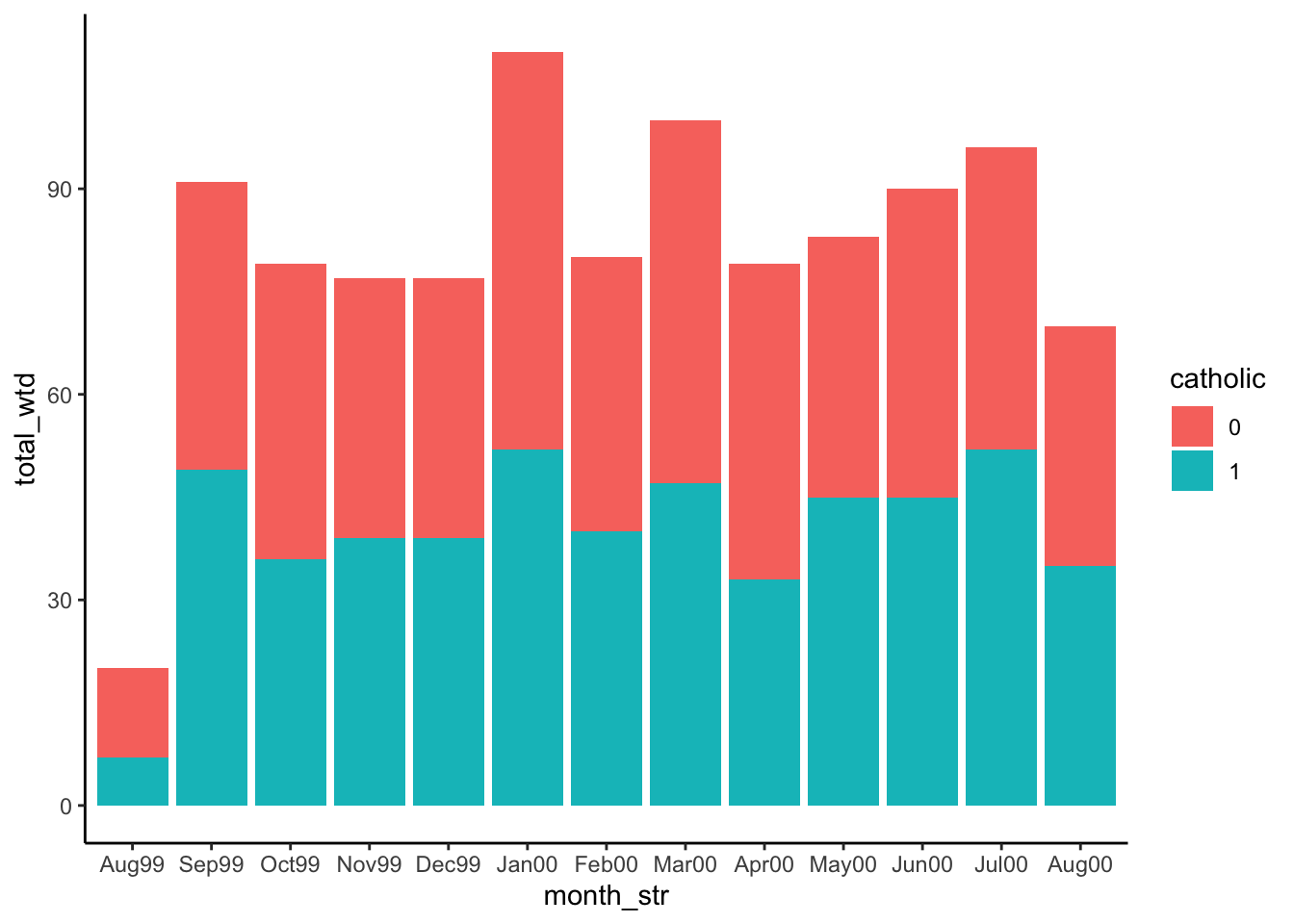
(Sanity check: wtd_df = students who want to drop, per month)

Code 
wtd_df <- student_df |> group_by(month_str, catholic) |>
  summarize(total_wtd=sum(wants_to_drop))
`summarise()` has grouped output by 'month_str'. You can override using the
`.groups` argument.
Code 
wtd_df |> ggplot(aes(x=month_str, y=total_wtd, fill=catholic)) +
  geom_bar(stat='identity') +
  theme_classic()

Compute Total Years (with Decimals) of Schooling

Code 
grad_day <- lubridate::make_date(2018, 6, 18)
student_df <- student_df |> mutate(
  schooling_start = lubridate::make_date(2005, 8, 26),
  schooling_end = as_date(ifelse(dropout==1, as_date(turns_18), as_date(grad_day))),
  school_days = difftime(schooling_end, schooling_start, units="days"),
  school_yrs = interval(schooling_start, schooling_end) / years(1)
)
student_df |> head()
day_of_yr catholic dob turns_18 year_abbr month_str can_drop_out wants_to_drop dropout schooling_start schooling_end school_days school_yrs
0 0 1999-08-26 2017-08-25 1999 Aug99 1 0 0 2005-08-26 2018-06-18 4679 days 12.81096
0 0 1999-08-26 2017-08-25 1999 Aug99 1 0 0 2005-08-26 2018-06-18 4679 days 12.81096
0 1 1999-08-26 2017-08-25 1999 Aug99 1 0 0 2005-08-26 2018-06-18 4679 days 12.81096
0 1 1999-08-26 2017-08-25 1999 Aug99 1 0 0 2005-08-26 2018-06-18 4679 days 12.81096
0 0 1999-08-26 2017-08-25 1999 Aug99 1 0 0 2005-08-26 2018-06-18 4679 days 12.81096
0 0 1999-08-26 2017-08-25 1999 Aug99 1 0 0 2005-08-26 2018-06-18 4679 days 12.81096

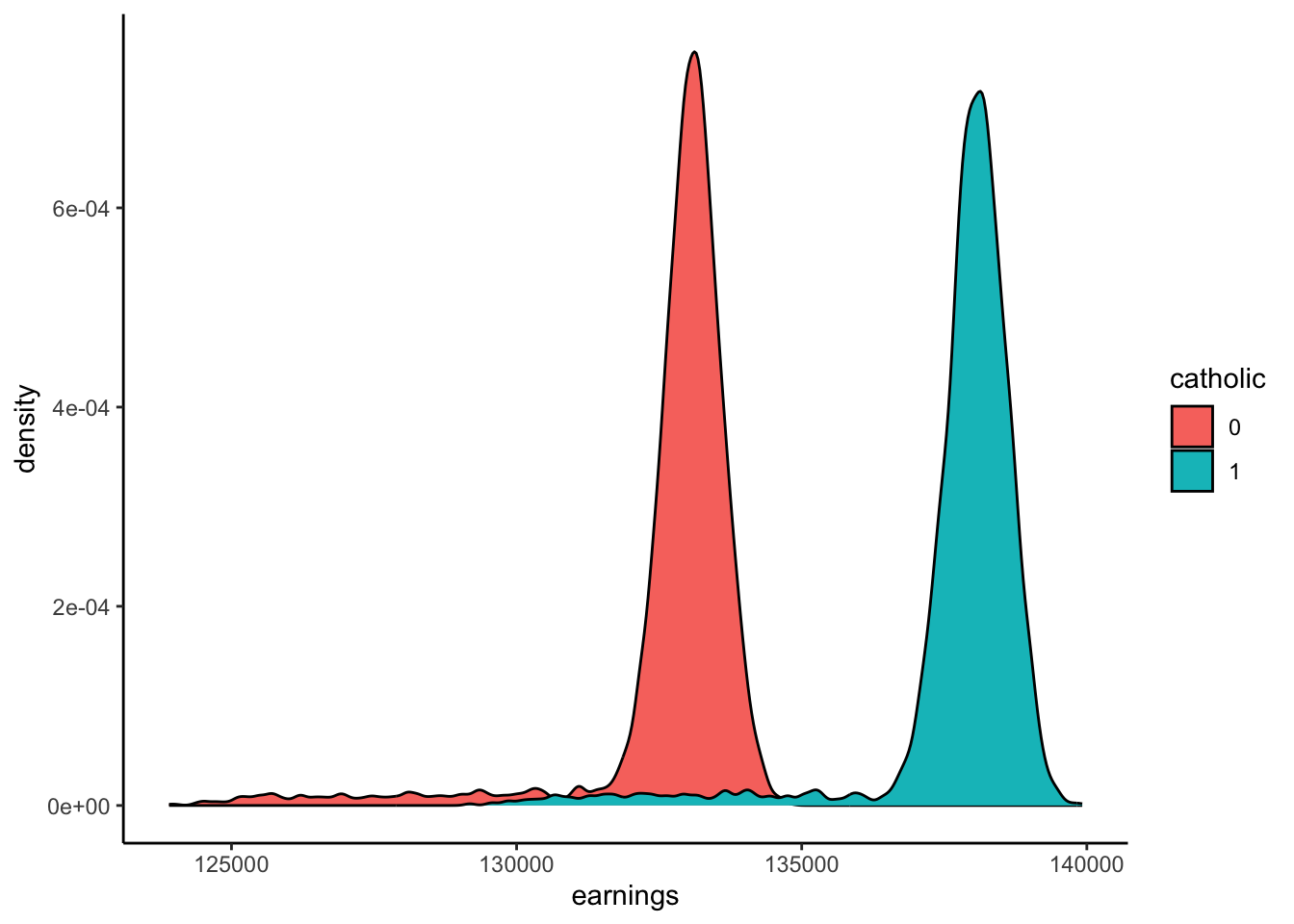
Simulated Earnings \(n\) Years Later

Code 
student_df$earnings_noise <- rnorm(nrow(student_df), 0, 500)
student_df <- student_df |> mutate(
  earnings = 10000 * school_yrs + 5000 * as.numeric(catholic) + earnings_noise
)
student_df |> ggplot(aes(x=earnings, fill=catholic)) + 
  geom_density() +
  theme_classic()

Code 
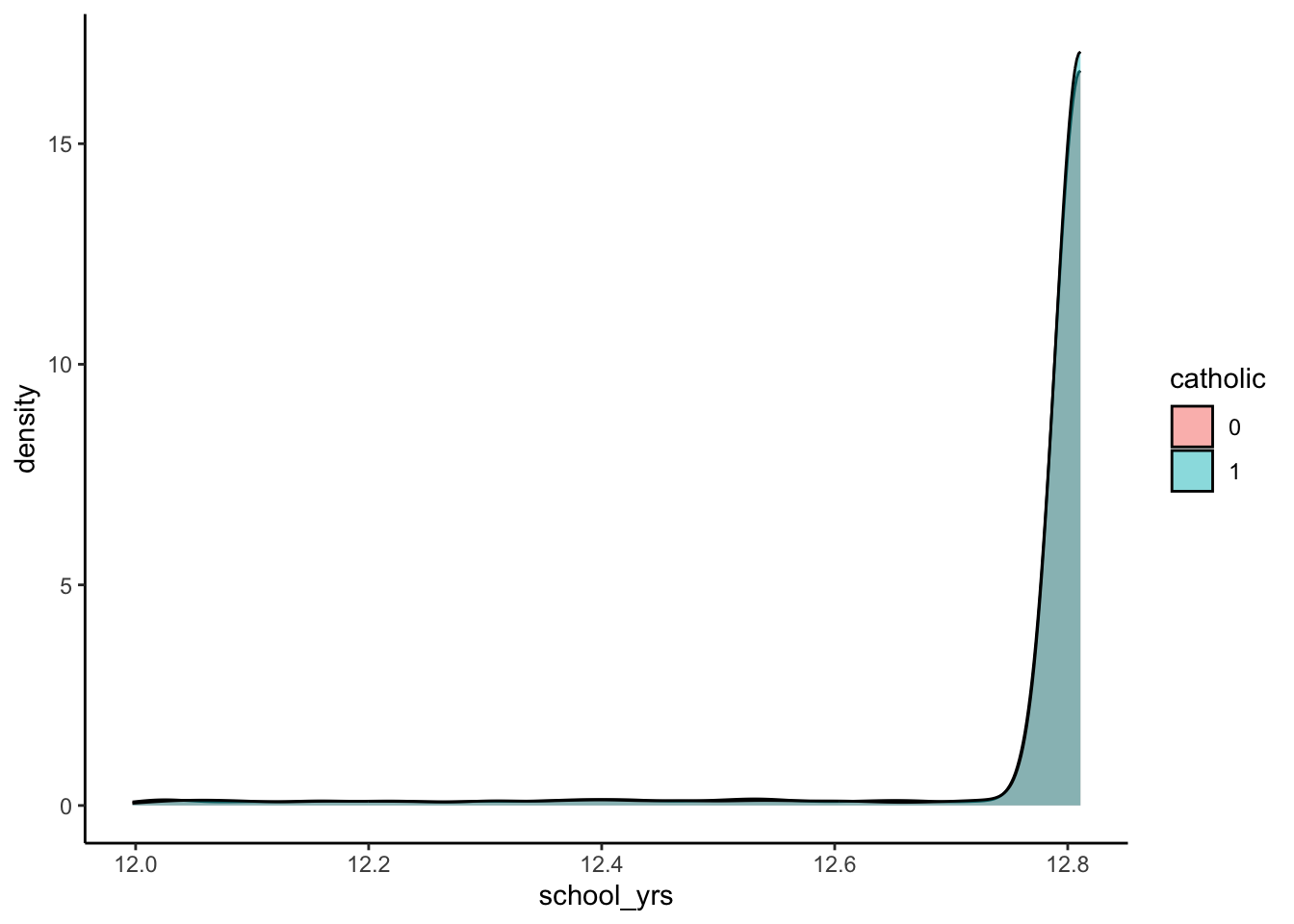
student_df |> ggplot(aes(x=school_yrs, fill=catholic)) +
  geom_density(alpha=0.5) +
  theme_classic()

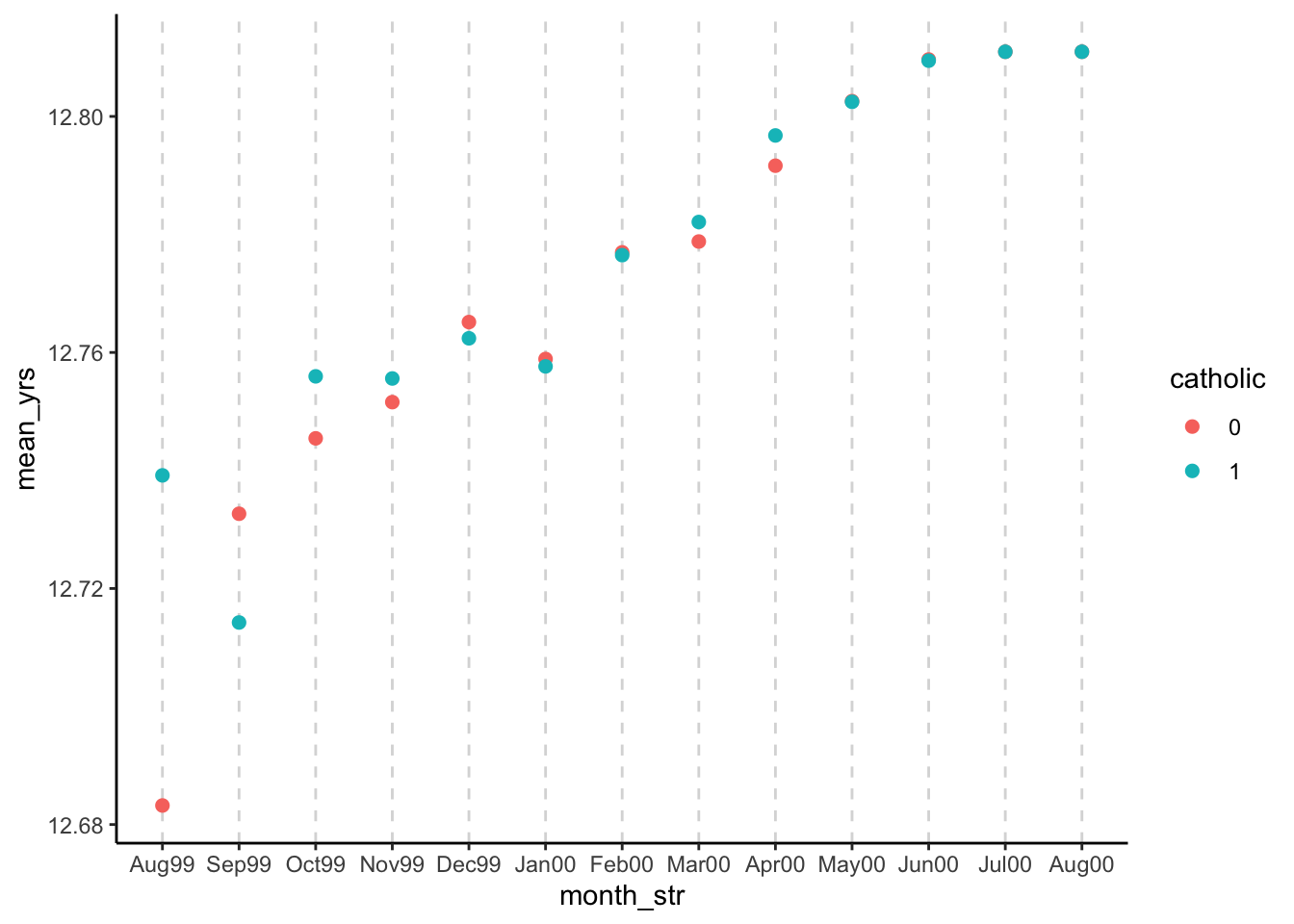
Mean Years of Schooling by Birth Month

Code 
schooling_df <- student_df |> group_by(month_str, catholic) |> summarize(
  mean_yrs=mean(school_yrs),
  n=n()
)
`summarise()` has grouped output by 'month_str'. You can override using the
`.groups` argument.
Code 
# Plot mean school days by month
schooling_df |> ggplot(aes(x=month_str, y=mean_yrs, color=catholic)) +
  geom_vline(aes(xintercept=month_str), linetype='dashed', linewidth=0.5, alpha=0.18) +
  geom_point(size=2) +
  theme_classic()

Code 
(max_schooling <- max(student_df$school_yrs))
[1] 12.81096
Code 
q1 <- c("Aug99","Sep99","Oct99","Nov99")
q2 <- c("Dec99","Jan00","Feb00")
q3 <- c("Mar00","Apr00","May00")
q4 <- c("Jun00","Jul00","Aug00")
schooling_df <- schooling_df |> mutate(
  qtr = case_match(
    month_str,
    q1 ~ 1,
    q2 ~ 2,
    q3 ~ 3,
    q4 ~ 4
  )
)
qtr_df <- schooling_df |> group_by(qtr, catholic) |> summarize(
  mean_yrs_qtr=mean(mean_yrs),
  n_qtr=sum(n)
)
`summarise()` has grouped output by 'qtr'. You can override using the `.groups`
argument.
Code 
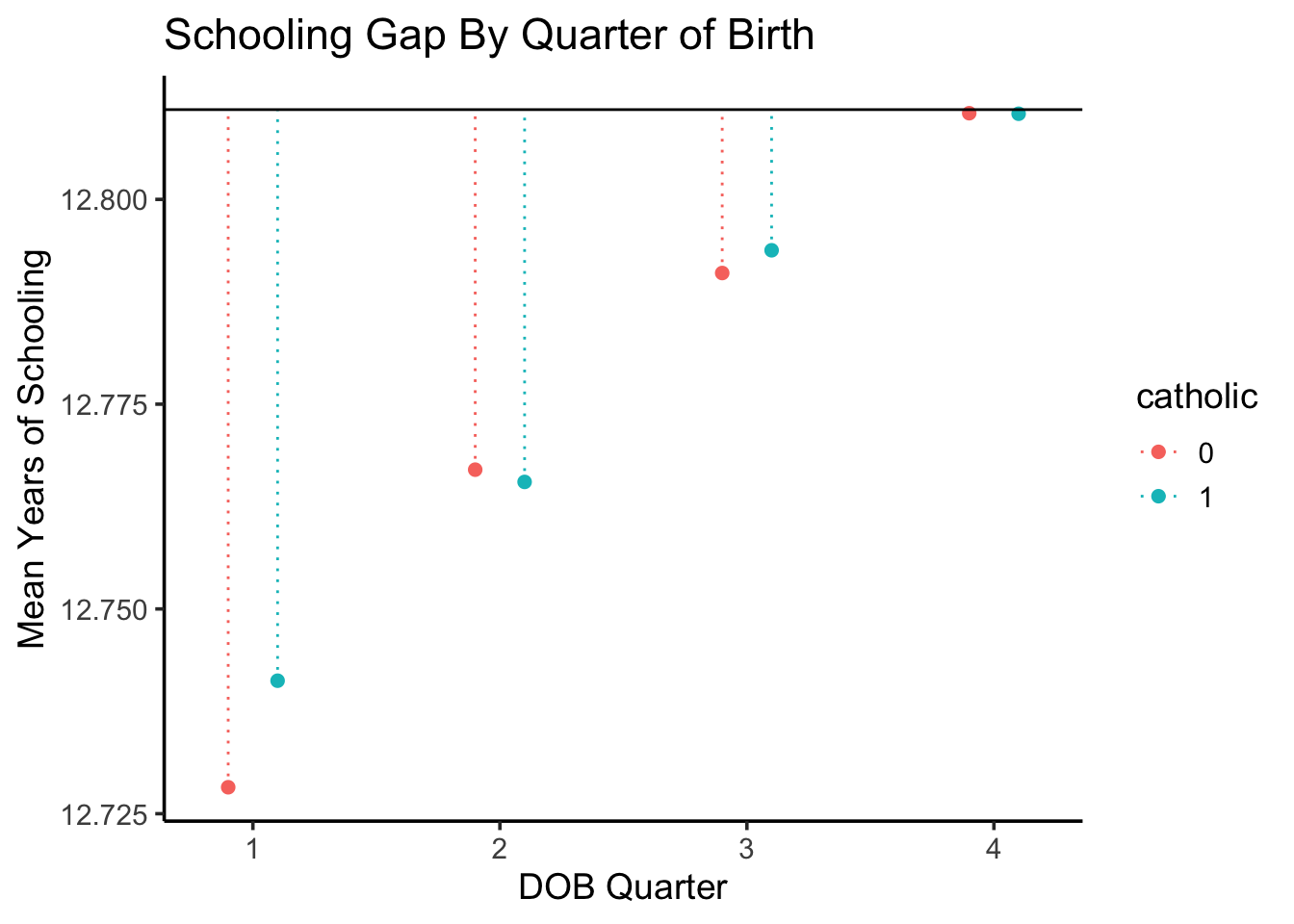
qtr_df |> ggplot(aes(x=qtr, y=mean_yrs_qtr, color=catholic)) +
  geom_point(
    stat='identity', size=2, position=position_dodge2(width=0.4)
  ) +
  geom_segment(
    aes(yend=max_schooling),
    # position=position_jitterdodge(
    #   #dodge.width=0.5
    # ),
    position=position_dodge2(width=0.4),
    linetype='dotted', linewidth=0.5
  ) +
  # ylim(12.759, 12.82) +
  geom_hline(
    aes(
      yintercept=max_schooling,
      #linetype='Max Possible'
    ),
    linewidth=0.5
  ) +
  # scale_linetype_manual("", values=c("dashed")) +
  # geom_text(x=2.5, y=12.81, label='Maximum Possible (Non-Dropout Amount)', vjust=-1) +
  labs(
    title="Schooling Gap By Quarter of Birth",
    x="DOB Quarter",
    y="Mean Years of Schooling"
  ) +
  theme_classic(base_size=14)

Code 
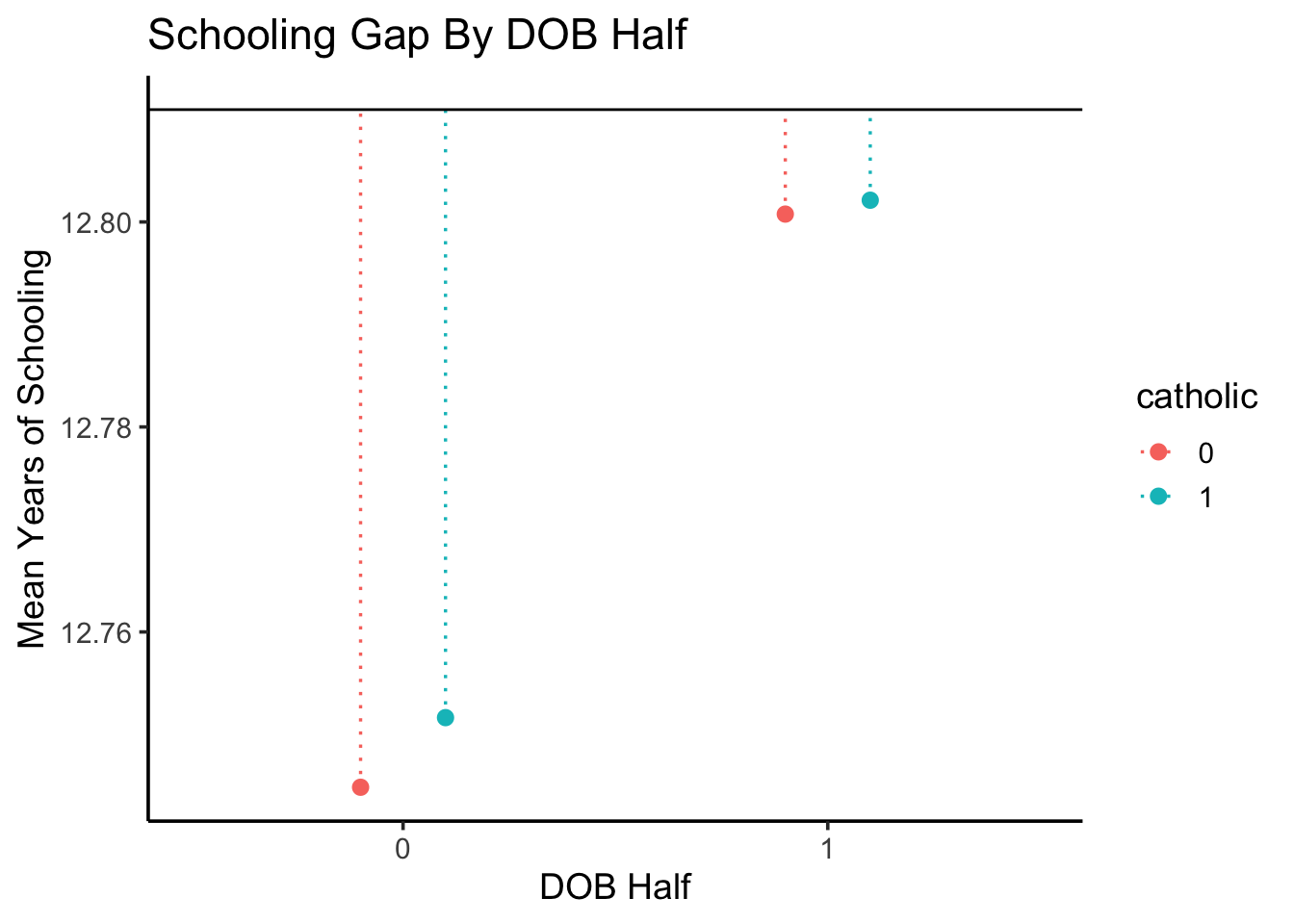
schooling_df <- schooling_df |> mutate(
  half = factor(
    ifelse(qtr==1 | qtr==2, 0, 1),
    levels=c(0,1)
  )
)
half_df <- schooling_df |> group_by(half, catholic) |> summarize(
  mean_yrs_half=mean(mean_yrs),
  n_half=sum(n)
)
`summarise()` has grouped output by 'half'. You can override using the
`.groups` argument.
Code 
half_df |> ggplot(aes(x=half, y=mean_yrs_half, color=catholic)) +
  geom_point(
    stat='identity', size=2.5,
    position=position_dodge2(width=0.4)
  ) +
  geom_segment(
    aes(yend=max_schooling),
    position=position_dodge2(width=0.4),
    linetype='dotted', linewidth=0.6
  ) +
  # ylim(12.759, 12.82) +
  geom_hline(
    aes(
      yintercept=max_schooling,
      #linetype='Max Possible'
    ),
    linewidth=0.5
  ) +
  # scale_linetype_manual("", values=c("dashed")) +
  # geom_text(x=1.5, y=12.81, label='Maximum Possible (Non-Dropout Amount)', vjust=-1) +
  labs(
    title="Schooling Gap By DOB Half",
    x="DOB Half",
    y="Mean Years of Schooling"
  ) +
  #xlim(0.5, 2.5) +
  # ylim(12.76, 12.82) +
  theme_classic(base_size=14)

Code 
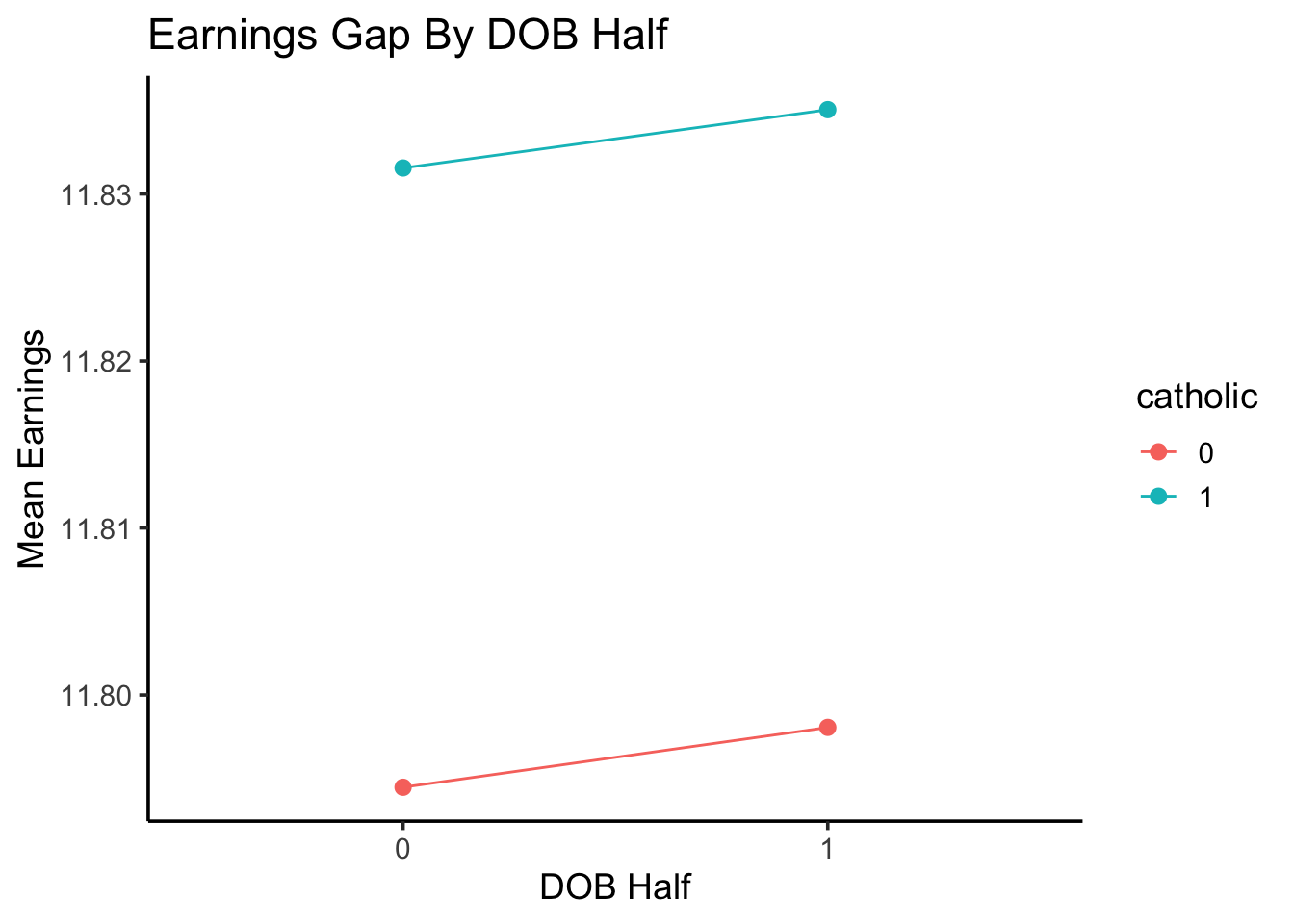
h0 <- c("Aug99","Sep99","Oct99","Nov99","Dec99","Jan00","Feb00")
h1 <- c("Mar00","Apr00","May00","Jun00","Jul00","Aug00")
student_df <- student_df |> mutate(
  half = factor(
    ifelse(month_str %in% h0, 0, 1),
    levels=c(0,1)
  )
)
earn_df <- student_df |> group_by(half, catholic) |>
  summarize(mean_earnings=mean(earnings))
`summarise()` has grouped output by 'half'. You can override using the
`.groups` argument.
Code 
earn_df
half catholic mean_earnings
0 0 132518.2
0 1 137524.1
1 0 132994.3
1 1 138005.8
Code 
# earn_df |> pivot_wider(-half)
earn_df |> ggplot(aes(x=half, y=log(mean_earnings), color=catholic, group=catholic)) +
  geom_point(stat='identity', size=2.5) +
  geom_line() +
  # ylim(12.759, 12.82) +
  # scale_linetype_manual("", values=c("dashed")) +
  labs(
    title="Earnings Gap By DOB Half",
    x="DOB Half",
    y="Mean Earnings"
  ) +
  #xlim(0.5, 2.5) +
  # ylim(127400, 128100) +
  theme_classic(base_size=14)

Code 
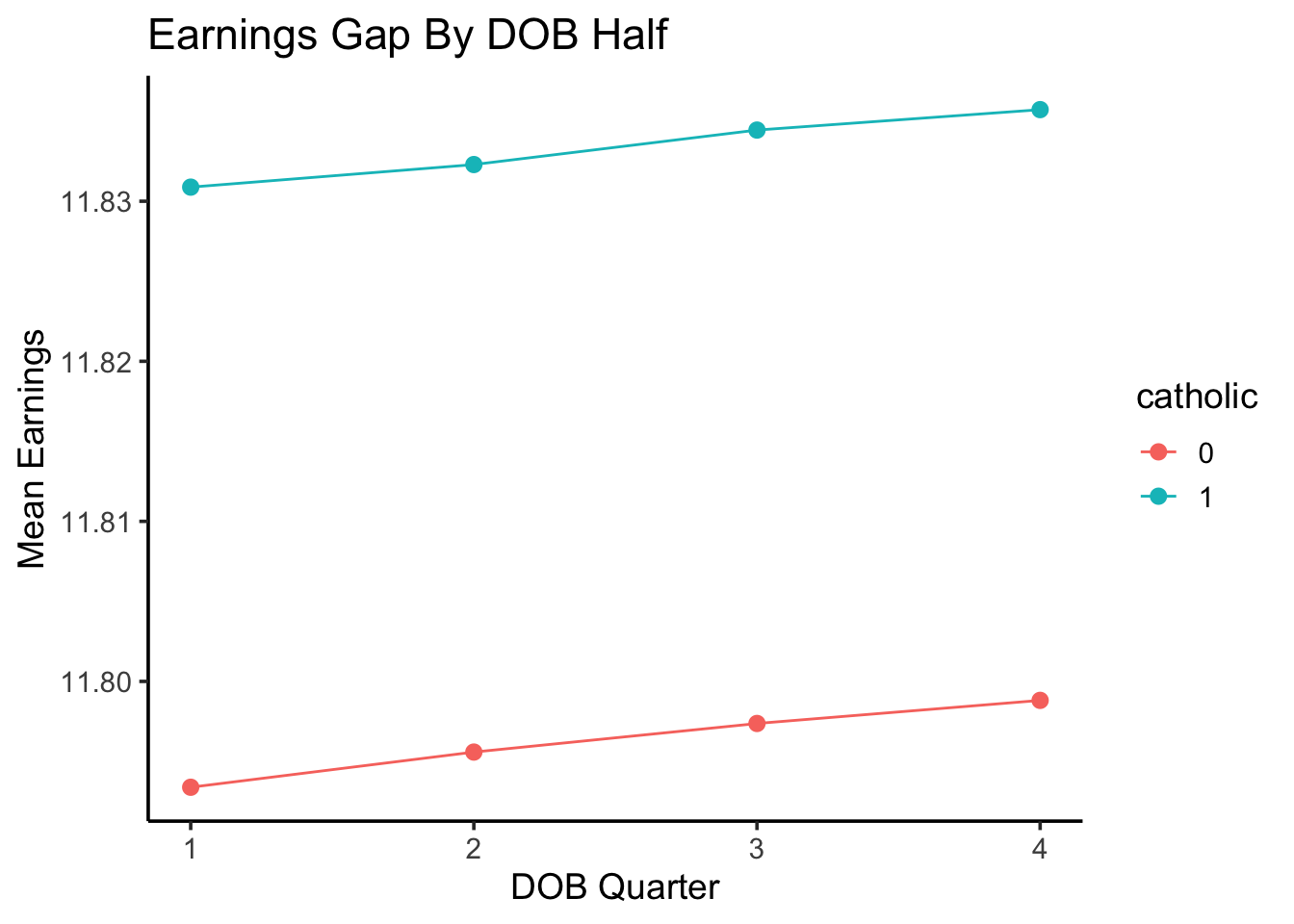
student_df <- student_df |> mutate(
  qtr = case_match(
    month_str,
    q1 ~ 1,
    q2 ~ 2,
    q3 ~ 3,
    q4 ~ 4
  )
)
earn_df <- student_df |> group_by(qtr, catholic) |>
  summarize(mean_earnings=mean(earnings))
`summarise()` has grouped output by 'qtr'. You can override using the `.groups`
argument.
Code 
earn_df
qtr catholic mean_earnings
1 0 132374.0
1 1 137431.5
2 0 132665.2
2 1 137625.5
3 0 132902.5
3 1 137922.4
4 0 133094.5
4 1 138098.6
Code 
# earn_df |> pivot_wider(-half)
earn_df |> ggplot(aes(x=qtr, y=log(mean_earnings), color=catholic, group=catholic)) +
  geom_point(stat='identity', size=2.5) +
  geom_line() +
  # ylim(12.759, 12.82) +
  # scale_linetype_manual("", values=c("dashed")) +
  labs(
    title="Earnings Gap By DOB Half",
    x="DOB Quarter",
    y="Mean Earnings"
  ) +
  #xlim(0.5, 2.5) +
  # ylim(127400, 128100) +
  theme_classic(base_size=14)

Code 
lm(mean_earnings ~ as.numeric(qtr), data=earn_df)

Call:
lm(formula = mean_earnings ~ as.numeric(qtr), data = earn_df)

Coefficients:
    (Intercept)  as.numeric(qtr)  
       134677.1            234.9
Code 
lm(as.numeric(catholic) ~ as.numeric(qtr), data=earn_df)

Call:
lm(formula = as.numeric(catholic) ~ as.numeric(qtr), data = earn_df)

Coefficients:
    (Intercept)  as.numeric(qtr)  
      1.500e+00        2.402e-16
Code 
lm(mean_earnings ~ as.numeric(catholic), data=earn_df)

Call:
lm(formula = mean_earnings ~ as.numeric(catholic), data = earn_df)

Coefficients:
         (Intercept)  as.numeric(catholic)  
              127749                  5010

References

Angrist, Joshua D., and Alan B. Krueger. 1991. “Does Compulsory School Attendance Affect Schooling and Earnings?” The Quarterly Journal of Economics 106 (4): 979–1014. https://doi.org/10.2307/2937954.