Week 2: Linear Regression

DSAN 5300: Statistical Learning
Spring 2026, Georgetown University

Class Sessions
Author
Affiliation

Jeff Jacobs

jj1088@georgetown.edu

Published

Monday, January 12, 2026

Open slides in new tab →

Schedule

Today’s Planned Schedule:

Start End Topic
Lecture 6:30pm 7:10pm Simple Linear Regression →
7:10pm 7:30pm Deriving the OLS Solution →
7:30pm 8:00pm Interpreting OLS Output →
Break! 8:00pm 8:10pm
8:10pm 8:30pm Quiz Review →
8:30pm 9:00pm Quiz 2!

Linear Regression

  • What happens to my dependent variable \(Y\) when my independent variable \(X\) increases by 1 unit?

  • Keep the goal in front of your mind:

    Tip The Goal of Regression

    Find a line \(\widehat{y} = mx + b\) that best predicts \(Y\) for given values of \(X\)

  • Sanity Note 1: \(\Rightarrow\) measuring error via vertical distance from line
  • Sanity Note 2: \(\Rightarrow\) modeling distribution of \(\boxed{Y \mid X}\), not \((X,Y)\)!
    • Predicting \(Y\) from \(X\) and \(X\) from \(Y\) \(\Rightarrow\) principal component line \(\neq\) regression!

How Do We Define “Best”?

  • Intuitively, two different ways to measure how well a line fits the data:
Code 
library(tidyverse)
set.seed(5321)
N <- 11
x <- seq(from = 0, to = 1, by = 1 / (N - 1))
y <- x + rnorm(N, 0, 0.2)
mean_y <- mean(y)
spread <- y - mean_y
df <- tibble(x = x, y = y, spread = spread)
ggplot(df, aes(x=x, y=y)) +
  geom_abline(slope=1, intercept=0, linetype="dashed", color=cbPalette[1], linewidth=g_linewidth*1.5) +
  geom_segment(xend=(x+y)/2, yend=(x+y)/2, linewidth=g_linewidth*2, color=cbPalette[2]) +
  geom_point(size=g_pointsize) +
  coord_equal() +
  xlim(0, 1) + ylim(0, 1) +
  dsan_theme("half") +
  labs(
    title = "Principal Component Line"
  )
ggplot(df, aes(x=x, y=y)) +
  geom_abline(slope=1, intercept=0, linetype="dashed", color=cbPalette[1], linewidth=g_linewidth*1.5) +
  geom_segment(xend=x, yend=x, linewidth=g_linewidth*2, color=cb_palette[3]) +
  geom_point(size=g_pointsize) +
  coord_equal() +
  xlim(0, 1) + ylim(0, 1) +
  dsan_theme("half") +
  labs(
    title = "Regression Line"
  )
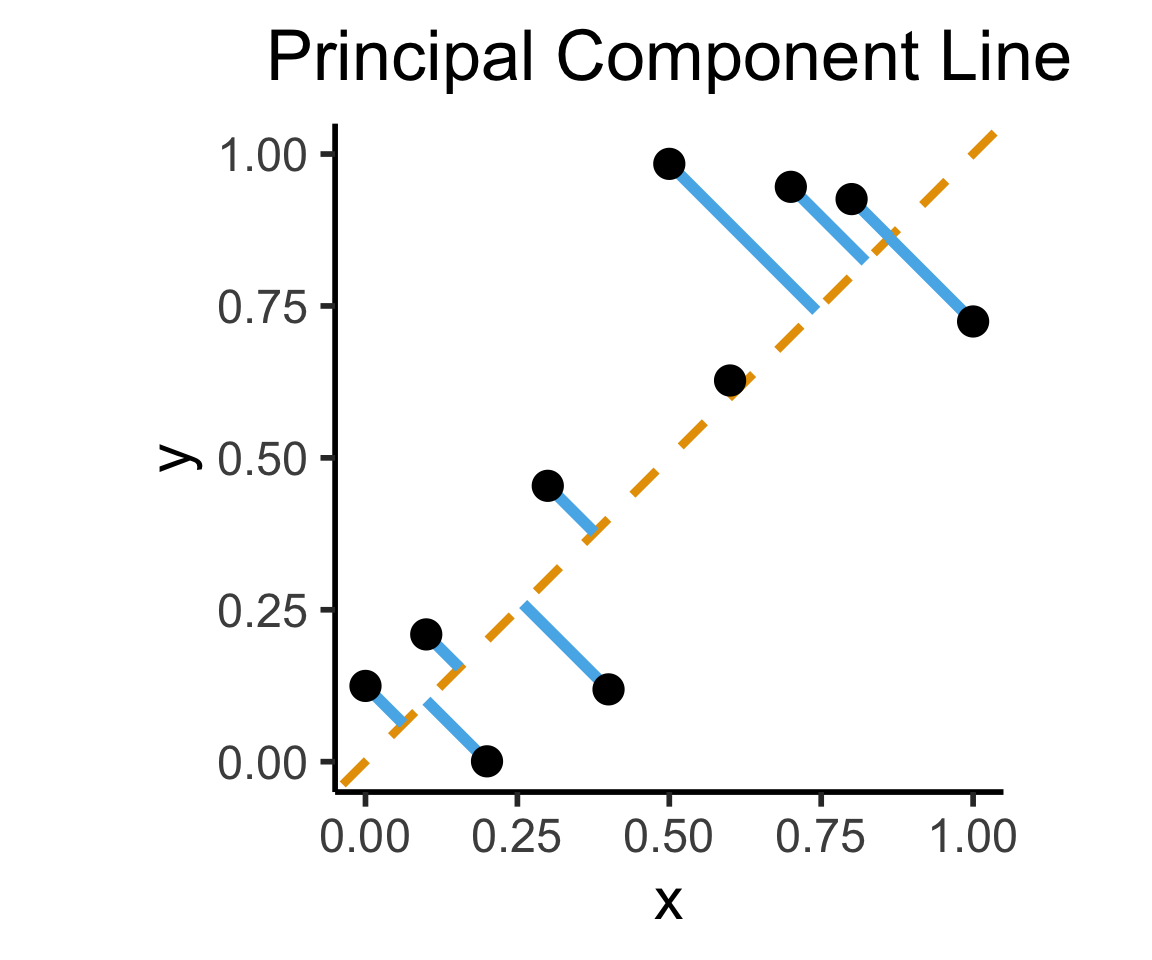
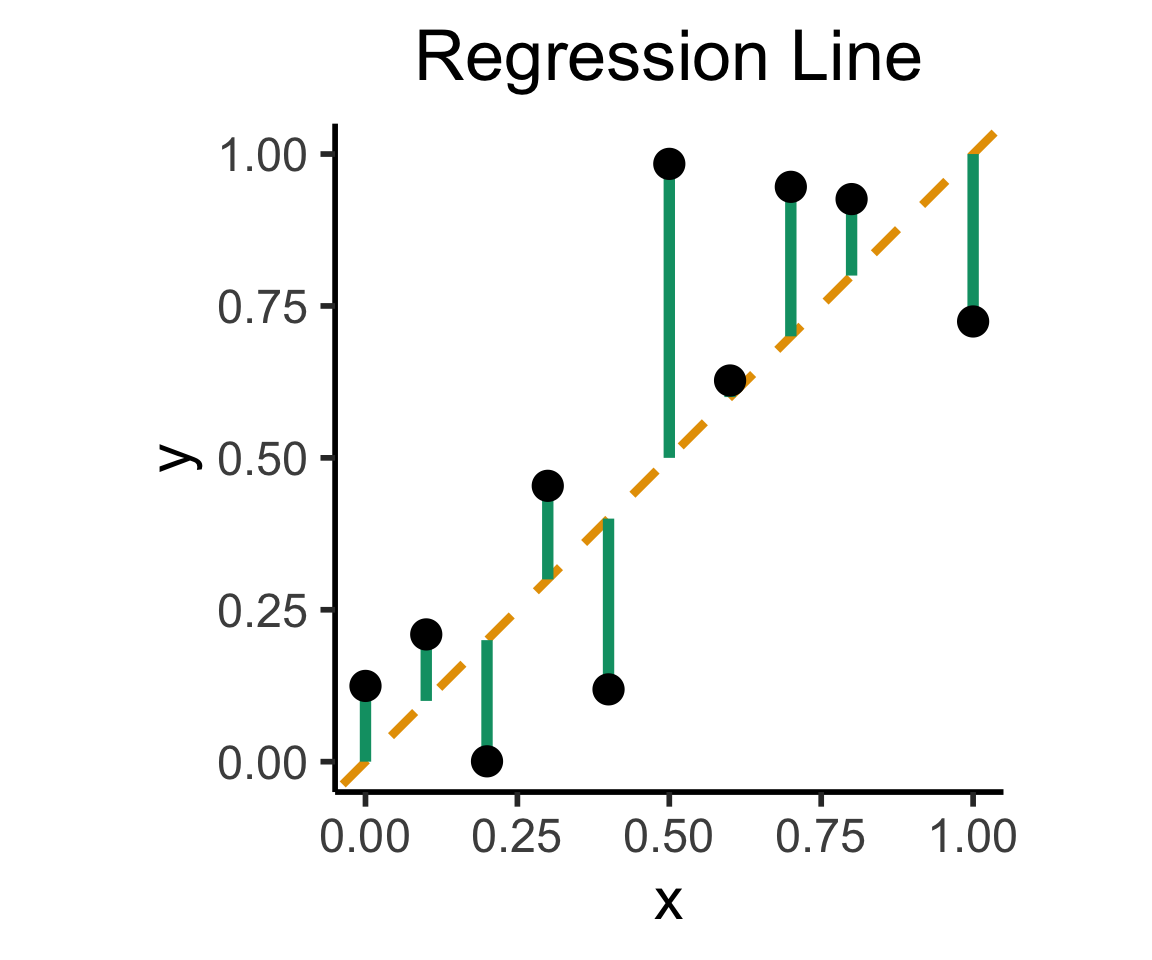
Figure 1: The line that minimizes blue distances does not predict \(Y\) as well as regression line, despite intuitive appeal!
Figure 2: The line that minimizes green distances optimally predicts \(Y\) from \(X\), in a mathematically-provable sense!

On the difference between these two lines, and why it matters, I cannot recommend Gelman and Hill (2007) enough!

Principal Component Analysis

  • Principal Component Line can be used to project the data onto its dimension of highest variance (recap from 5000!)
  • More simply: PCA can discover meaningful axes in data (unsupervised learning / exploratory data analysis settings)
Code 
library(readr)
library(ggplot2)
gdp_df <- read_csv("assets/gdp_pca.csv")

dist_to_line <- function(x0, y0, a, c) {
    numer <- abs(a * x0 - y0 + c)
    denom <- sqrt(a * a + 1)
    return(numer / denom)
}
# Finding PCA line for industrial vs. exports
x <- gdp_df$industrial
y <- gdp_df$exports
lossFn <- function(lineParams, x0, y0) {
    a <- lineParams[1]
    c <- lineParams[2]
    return(sum(dist_to_line(x0, y0, a, c)))
}
o <- optim(c(0, 0), lossFn, x0 = x, y0 = y)
ggplot(gdp_df, aes(x = industrial, y = exports)) +
    geom_point(size=g_pointsize/2) +
    geom_abline(aes(slope = o$par[1], intercept = o$par[2], color="pca"), linewidth=g_linewidth, show.legend = TRUE) +
    geom_smooth(aes(color="lm"), method = "lm", se = FALSE, linewidth=g_linewidth, key_glyph = "blank") +
    scale_color_manual(element_blank(), values=c("pca"=cbPalette[2],"lm"=cbPalette[1]), labels=c("Regression","PCA")) +
    dsan_theme("half") +
    remove_legend_title() +
    labs(
      title = "PCA Line vs. Regression Line",
        x = "Industrial Production (% of GDP)",
        y = "Exports (% of GDP)"
    )

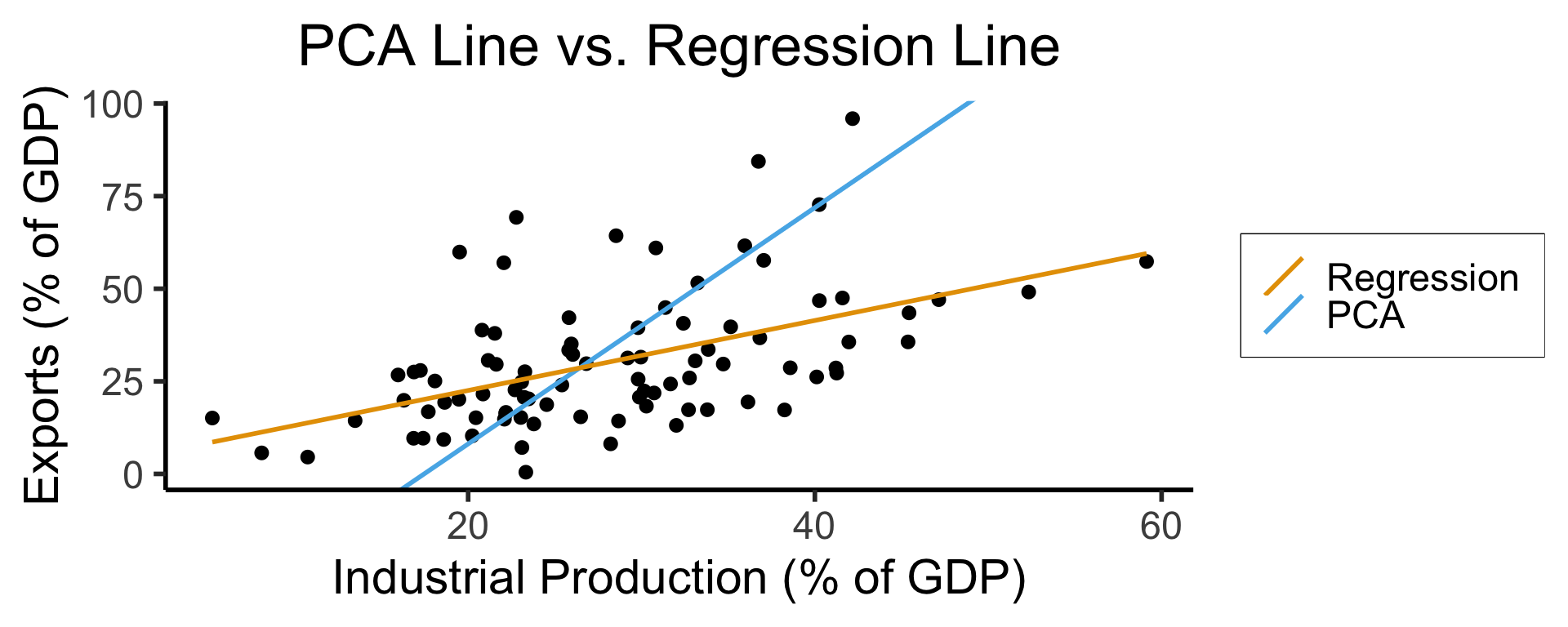
See this amazing blog post using PCA, with 2 dimensions, to explore UN voting patterns!

Create Your Own Dimension!

Code 
ggplot(gdp_df, aes(pc1, .fittedPC2)) +
    geom_point(size = g_pointsize/2) +
    geom_hline(aes(yintercept=0, color='PCA Line'), linetype='solid', size=g_linesize) +
    geom_rug(sides = "b", linewidth=g_linewidth/1.2, length = unit(0.1, "npc"), color=cbPalette[3]) +
    expand_limits(y=-1.6) +
    scale_color_manual(element_blank(), values=c("PCA Line"=cbPalette[2])) +
    dsan_theme("full") +
    remove_legend_title() +
    labs(
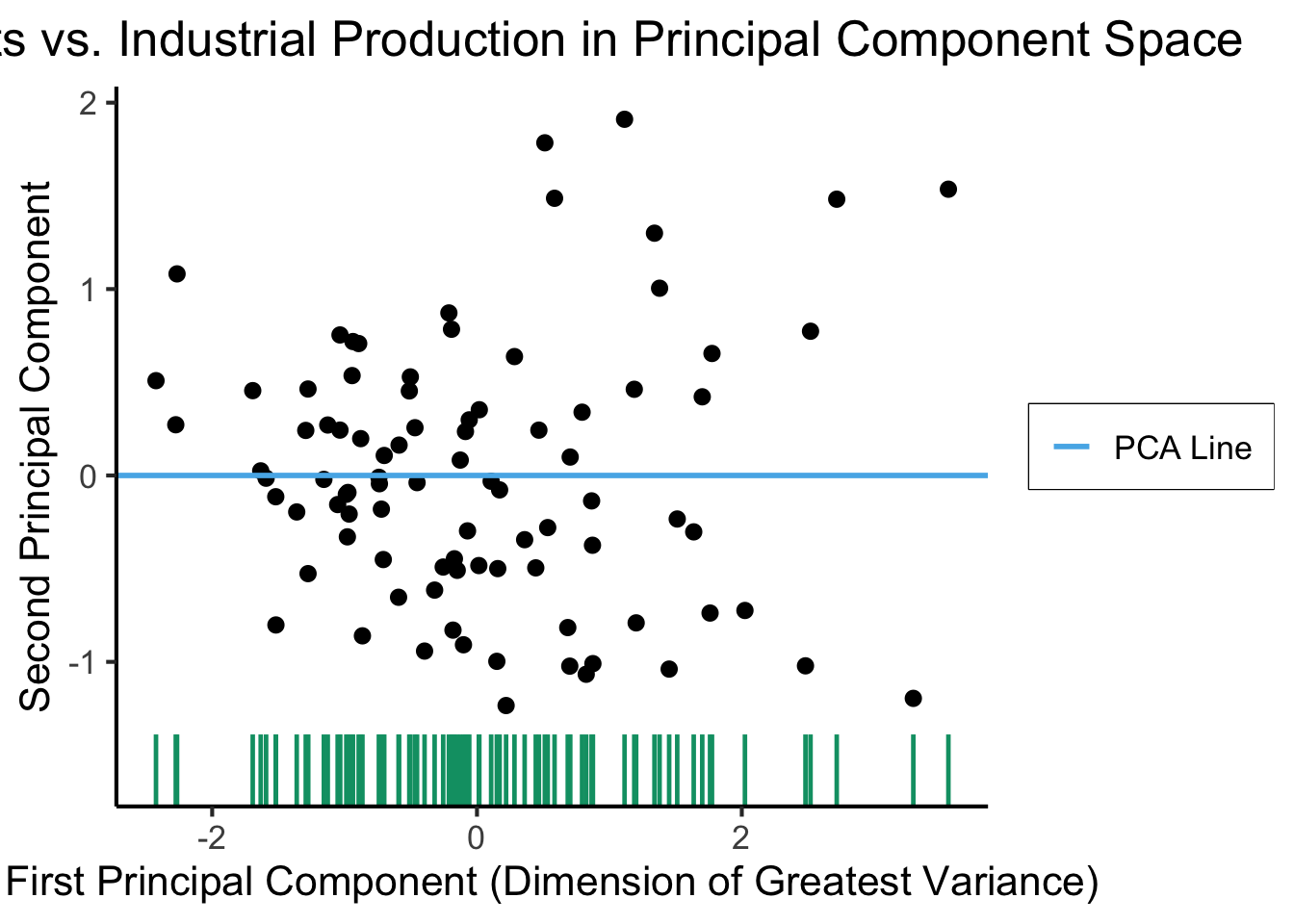
      title = "Exports vs. Industrial Production in Principal Component Space",
      x = "First Principal Component (Dimension of Greatest Variance)",
      y = "Second Principal Component"
    )

…And Use It for EDA

Code 
library(dplyr)
library(tidyr)
plot_df <- gdp_df %>% select(c(country_code, pc1, agriculture, military))
long_df <- plot_df %>% pivot_longer(!c(country_code, pc1), names_to = "var", values_to = "val")
long_df <- long_df |> mutate(
  var = case_match(
    var,
    "agriculture" ~ "Agricultural Production",
    "military" ~ "Military Spending"
  )
)
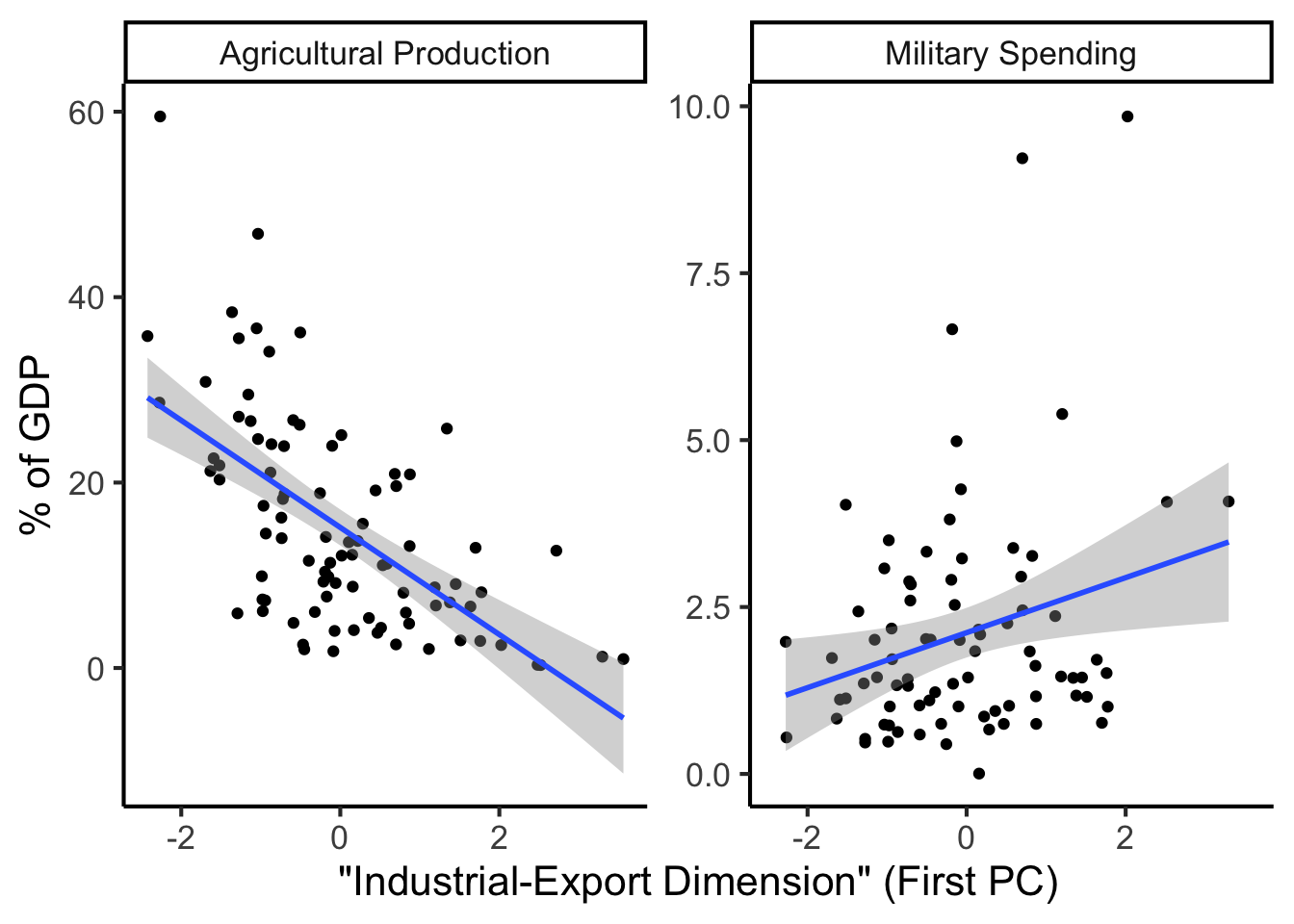
ggplot(long_df, aes(x = pc1, y = val, facet = var)) +
    geom_point() +
    geom_smooth(method=lm, formula='y ~ x') +
    facet_wrap(vars(var), scales = "free") +
    dsan_theme("full") +
    labs(
        x = "\"Industrial-Export Dimension\" (First PC)",
        y = "% of GDP"
    )

But in Our Case…

  • \(x\) and \(y\) dimensions already have meaning, and we have a hypothesis about effect of \(x\) on \(y\)!
TipThe Regression Hypothesis \(\mathcal{H}_{\text{reg}}\)

Given data \((X, Y)\), we estimate \(\widehat{y} = \widehat{\beta}_0 + \widehat{\beta}_1x\), hypothesizing that:

  • Starting from \(y = \underbrace{\widehat{\beta}_0}_{\mathclap{\text{Intercept}}}\) when \(x = 0\),
  • An increase of \(x\) by 1 unit is associated with an increase of \(y\) by \(\underbrace{\widehat{\beta}_1}_{\mathclap{\text{Coefficient}}}\) units
  • We want to measure how well our line predicts \(y\) for any given \(x\) value \(\implies\) vertical distance from regression line

Example: Advertising Effects

  • Independent variable: $ put into advertisements; Dependent variable: Sales
  • Goal 1: Predict sales for a given allocation
  • Goal 2: Infer best allocation for a given advertising budget (more simply: a new $1K appears! Where should we invest it?)
Code 
library(tidyverse)
ad_df <- read_csv("assets/Advertising.csv") |> rename(id=`...1`)
long_df <- ad_df |> pivot_longer(-c(id, sales), names_to="medium", values_to="allocation")
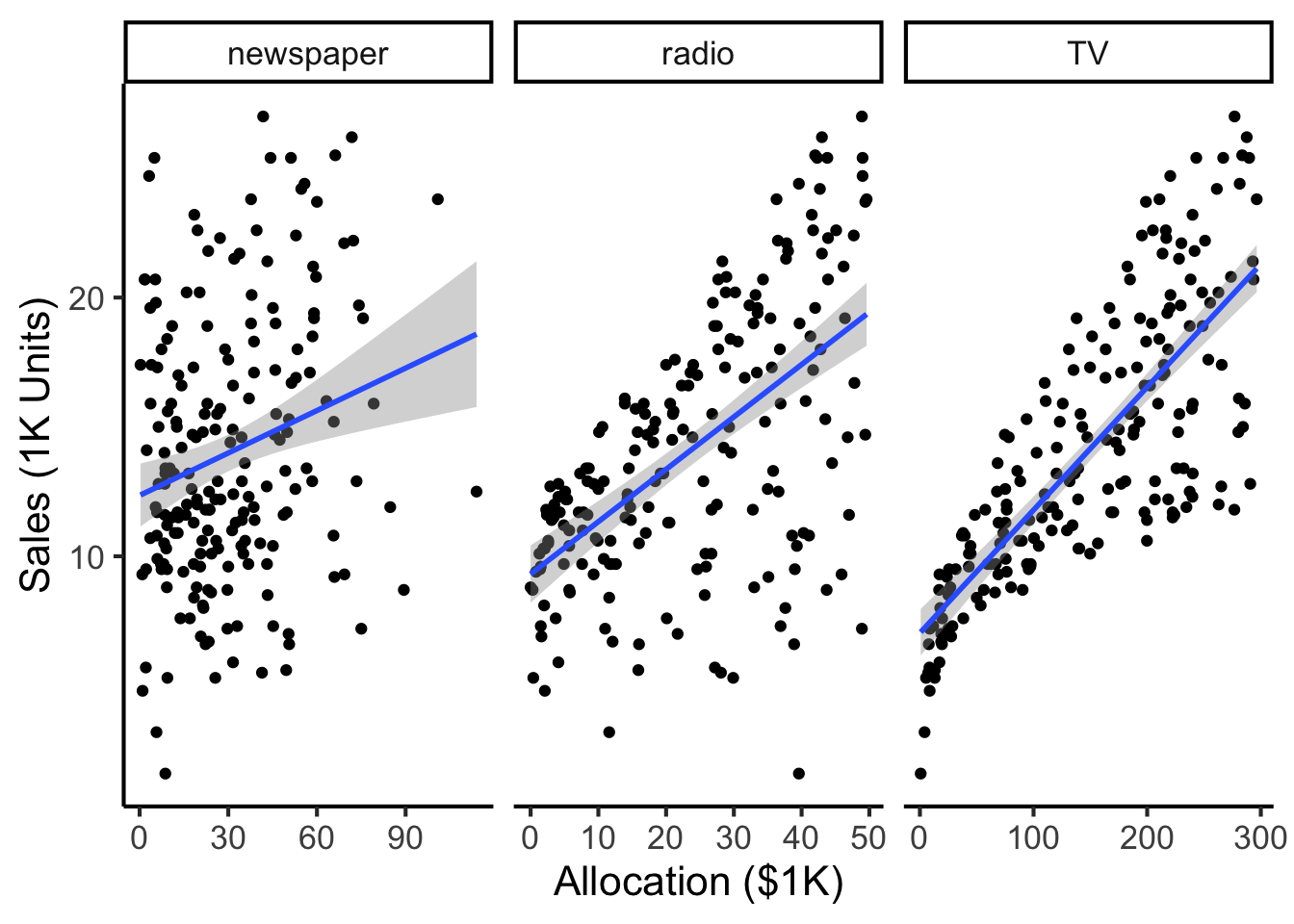
long_df |> ggplot(aes(x=allocation, y=sales)) +
  geom_point() +
  facet_wrap(vars(medium), scales="free_x") +
  geom_smooth(method='lm', formula="y ~ x") +
  theme_dsan() +
  labs(
    x = "Allocation ($1K)",
    y = "Sales (1K Units)"
  )

Simple Linear Regression

  • For now, we treat Newspaper, Radio, TV advertising separately: how much do sales increase per $1 into [medium]? (Later we’ll consider them jointly: multiple regression)

Our model:

\[ Y = \underbrace{\param{\beta_0}}_{\mathclap{\text{Intercept}}} + \underbrace{\param{\beta_1}}_{\mathclap{\text{Slope}}}X + \varepsilon \]

…Generates predictions via:

\[ \widehat{y} = \underbrace{\widehat{\beta}_0}_{\mathclap{\small\begin{array}{c}\text{Estimated} \\[-5mm] \text{intercept}\end{array}}} ~+~ \underbrace{\widehat{\beta}_1}_{\mathclap{\small\begin{array}{c}\text{Estimated} \\[-4mm] \text{slope}\end{array}}}\cdot x \]

  • Note how these predictions will be wrong (unless the data is perfectly linear)
  • We’ve accounted for this in our model (by including \(\varepsilon\) term)!
  • But, we’d like to find estimates \(\widehat{\beta}_0\) and \(\widehat{\beta}_1\) that produce the “least wrong” predictions: motivates focus on residuals \(\widehat{\varepsilon}_i\)…

\[ \widehat{\varepsilon}_i = \underbrace{y_i}_{\mathclap{\small\begin{array}{c}\text{Real} \\[-5mm] \text{label}\end{array}}} - \underbrace{\widehat{y}_i}_{\mathclap{\small\begin{array}{c}\text{Predicted} \\[-5mm] \text{label}\end{array}}} = \underbrace{y_i}_{\mathclap{\small\begin{array}{c}\text{Real} \\[-5mm] \text{label}\end{array}}} - \underbrace{ \left( \widehat{\beta}_0 + \widehat{\beta}_1 \cdot x \right) }_{\text{\small{Predicted label}}} \]

Least Squares: Minimizing Residuals

What can we optimize to ensure these residuals are as small as possible?

Code 
N <- 21
x <- seq(from = 0, to = 1, by = 1 / (N - 1))
y <- x + rnorm(N, 0, 0.25)
mean_y <- mean(y)
spread <- y - mean_y
sim_lg_df <- tibble(x = x, y = y, spread = spread)
sim_lg_df |> ggplot(aes(x=x, y=y)) +
  geom_abline(slope=1, intercept=0, linetype="dashed", color=cbPalette[1], linewidth=g_linewidth) +
  # geom_segment(xend=x, yend=x, linewidth=g_linewidth*2, color=cbPalette[2]) +
  geom_segment(aes(xend=x, yend=x, color=ifelse(y>x,"Positive","Negative")), linewidth=1.5*g_linewidth) +
  geom_point(size=g_pointsize) +
  # coord_equal() +
  theme_dsan("half") +
  scale_color_manual("Spread", values=c("Positive"=cbPalette[3],"Negative"=cbPalette[6]), labels=c("Positive"="Positive","Negative"="Negative"))
large_sum <- sum(sim_lg_df$spread)
writeLines(fmt_decimal(large_sum))
large_sqsum <- sum((sim_lg_df$spread)^2)
writeLines(fmt_decimal(large_sqsum))
large_abssum <- sum(abs(sim_lg_df$spread))
writeLines(fmt_decimal(large_abssum))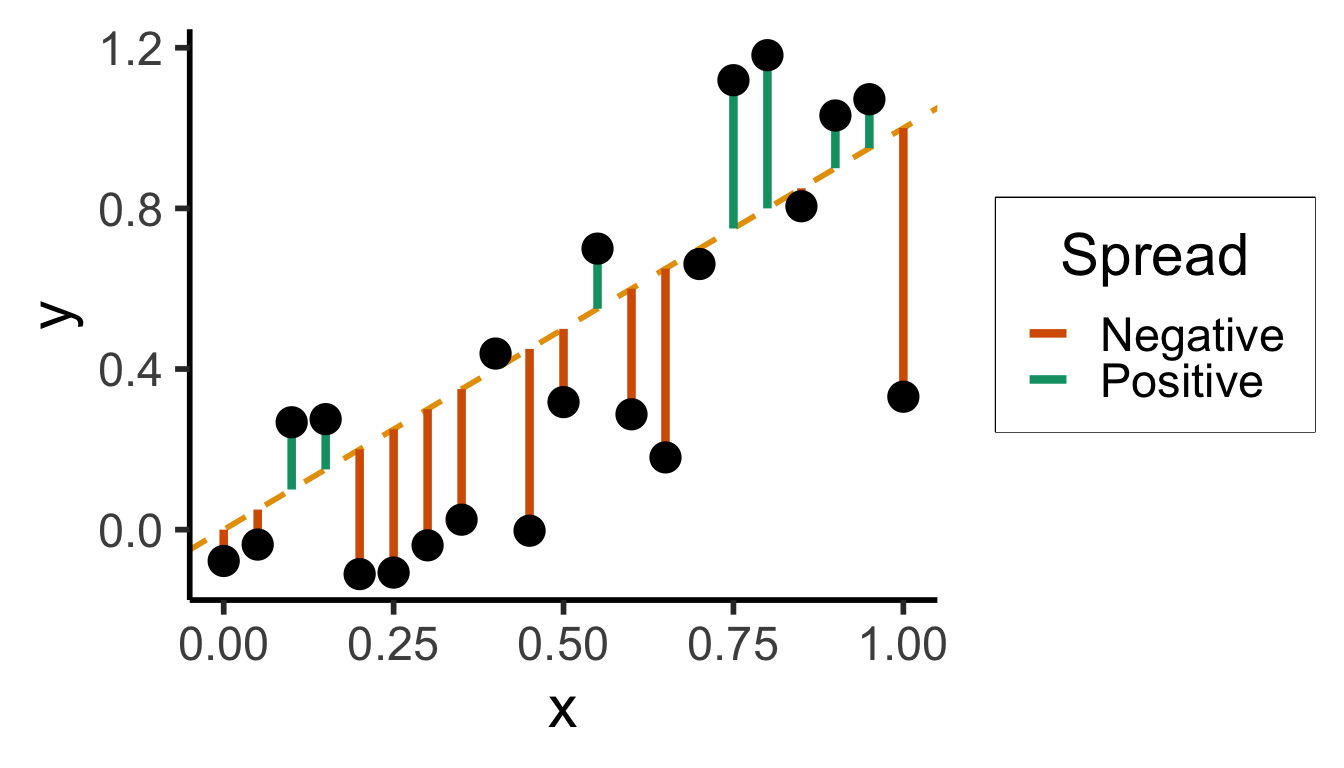

Sum?

0.0000000000

Sum of Squares?

3.8405017200

Sum of absolute vals?

7.6806094387
Code 
N <- 21
x <- seq(from = 0, to = 1, by = 1 / (N - 1))
y <- x + rnorm(N, 0, 0.05)
mean_y <- mean(y)
spread <- y - mean_y
sim_sm_df <- tibble(x = x, y = y, spread = spread)
sim_sm_df |> ggplot(aes(x=x, y=y)) +
  geom_abline(slope=1, intercept=0, linetype="dashed", color=cbPalette[1], linewidth=g_linewidth) +
  # geom_segment(xend=x, yend=x, linewidth=g_linewidth*2, color=cbPalette[2]) +
  geom_segment(aes(xend=x, yend=x, color=ifelse(y>x,"Positive","Negative")), linewidth=1.5*g_linewidth) +
  geom_point(size=g_pointsize) +
  # coord_equal() +
  theme_dsan("half") +
  scale_color_manual("Spread", values=c("Positive"=cbPalette[3],"Negative"=cbPalette[6]), labels=c("Positive"="Positive","Negative"="Negative"))
small_rsum <- sum(sim_sm_df$spread)
writeLines(fmt_decimal(small_rsum))
small_sqrsum <- sum((sim_sm_df$spread)^2)
writeLines(fmt_decimal(small_sqrsum))
small_abssum <- sum(abs(sim_sm_df$spread))
writeLines(fmt_decimal(small_abssum))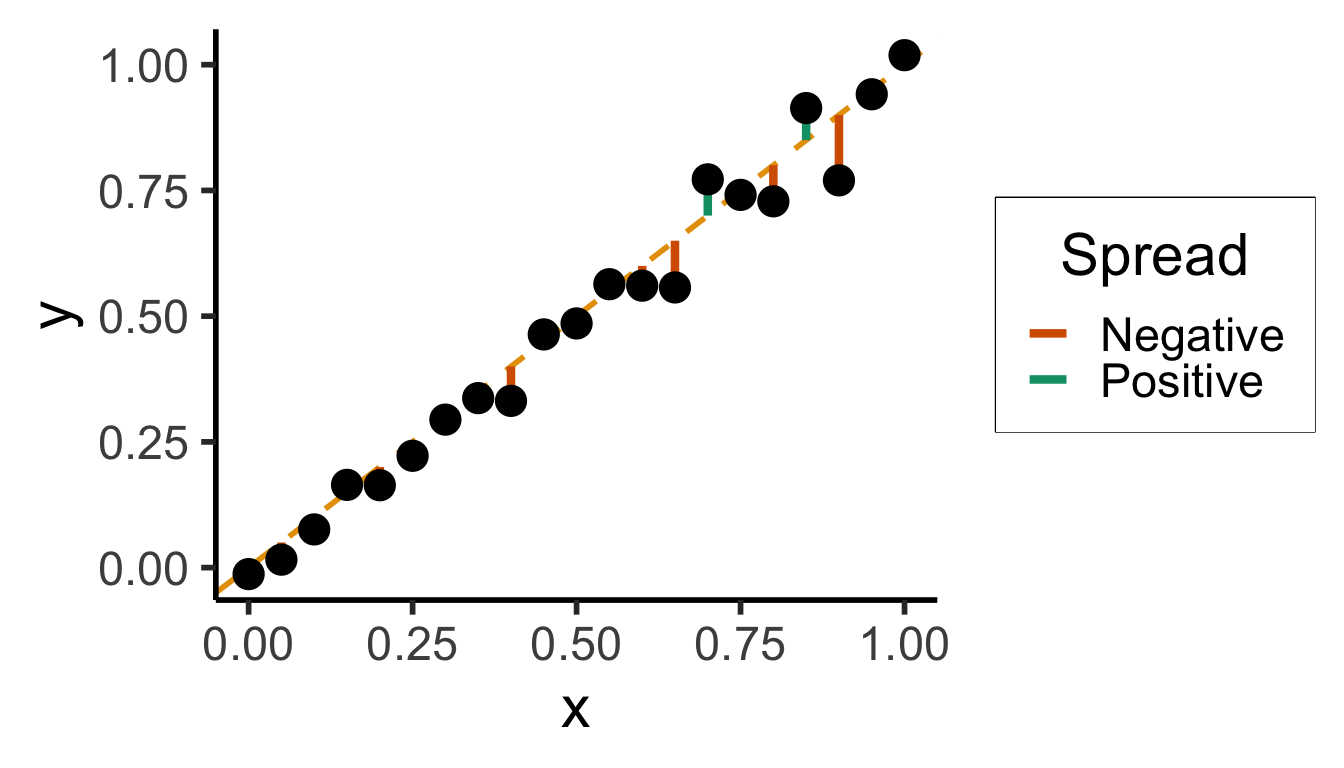

Sum?

0.0000000000

Sum of Squares?

1.9748635217

Sum of absolute vals?

5.5149697440

Why Not Absolute Value?

  • Two feasible ways to prevent positive and negative residuals cancelling out:
    • Absolute error \(\left|y - \widehat{y}\right|\) or squared error \(\left( y - \widehat{y} \right)^2\)
  • But remember: we’re aiming to minimize 👀 these residuals; ghost of calculus past 😱
  • We minimize by taking derivatives… which one is differentiable everywhere?
Code 
# Could use facet_grid() here, but it doesn't work too nicely with stat_function() :(
ggplot(data.frame(x=c(-4,4)), aes(x=x)) +
  stat_function(
    fun =~ abs(.x),
    linewidth=g_linewidth * 1.5,
    color=cb_palette[1],
  ) +
  dsan_theme("quarter") +
  labs(
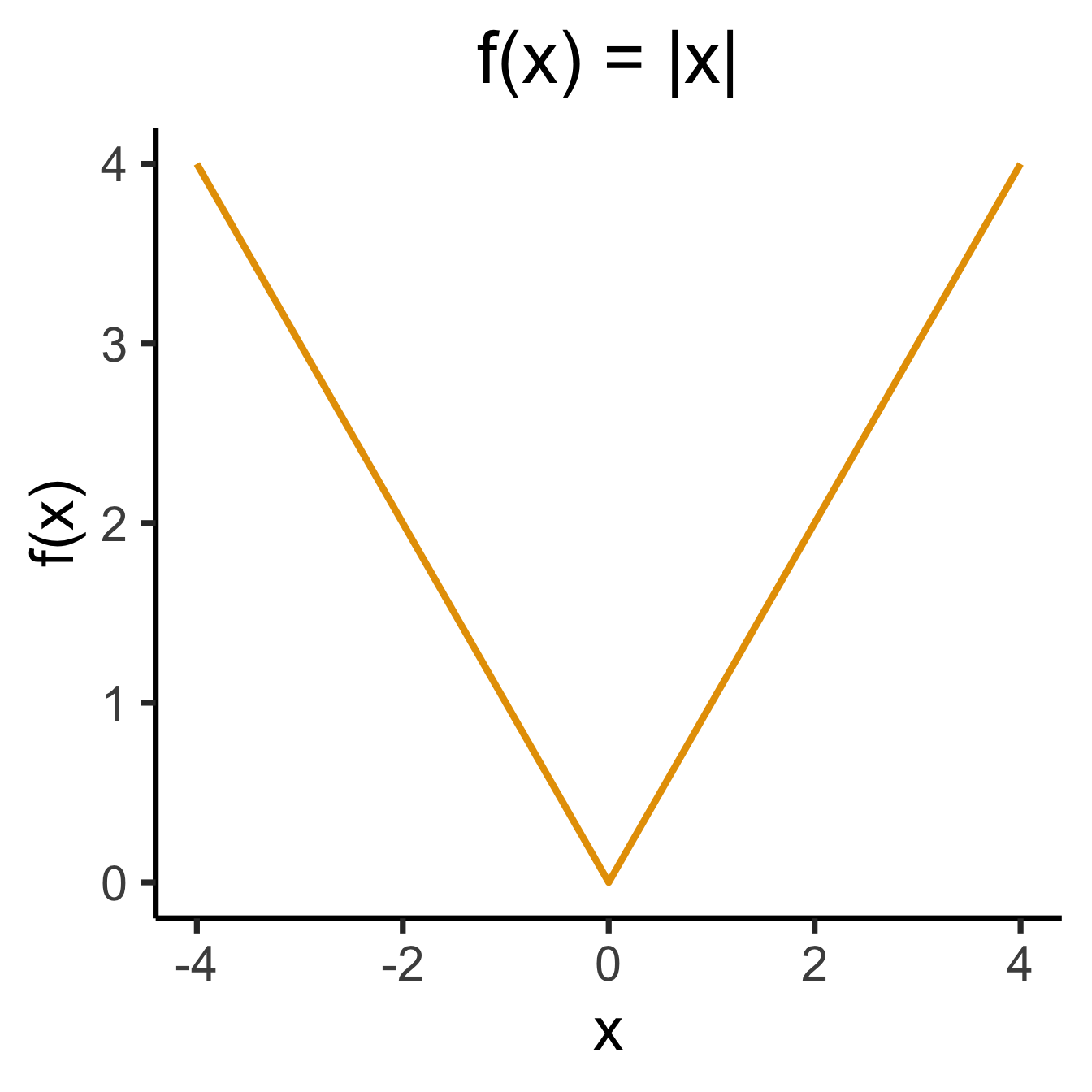
    title="f(x) = |x|",
    y="f(x)"
  )

Code 
library(latex2exp)
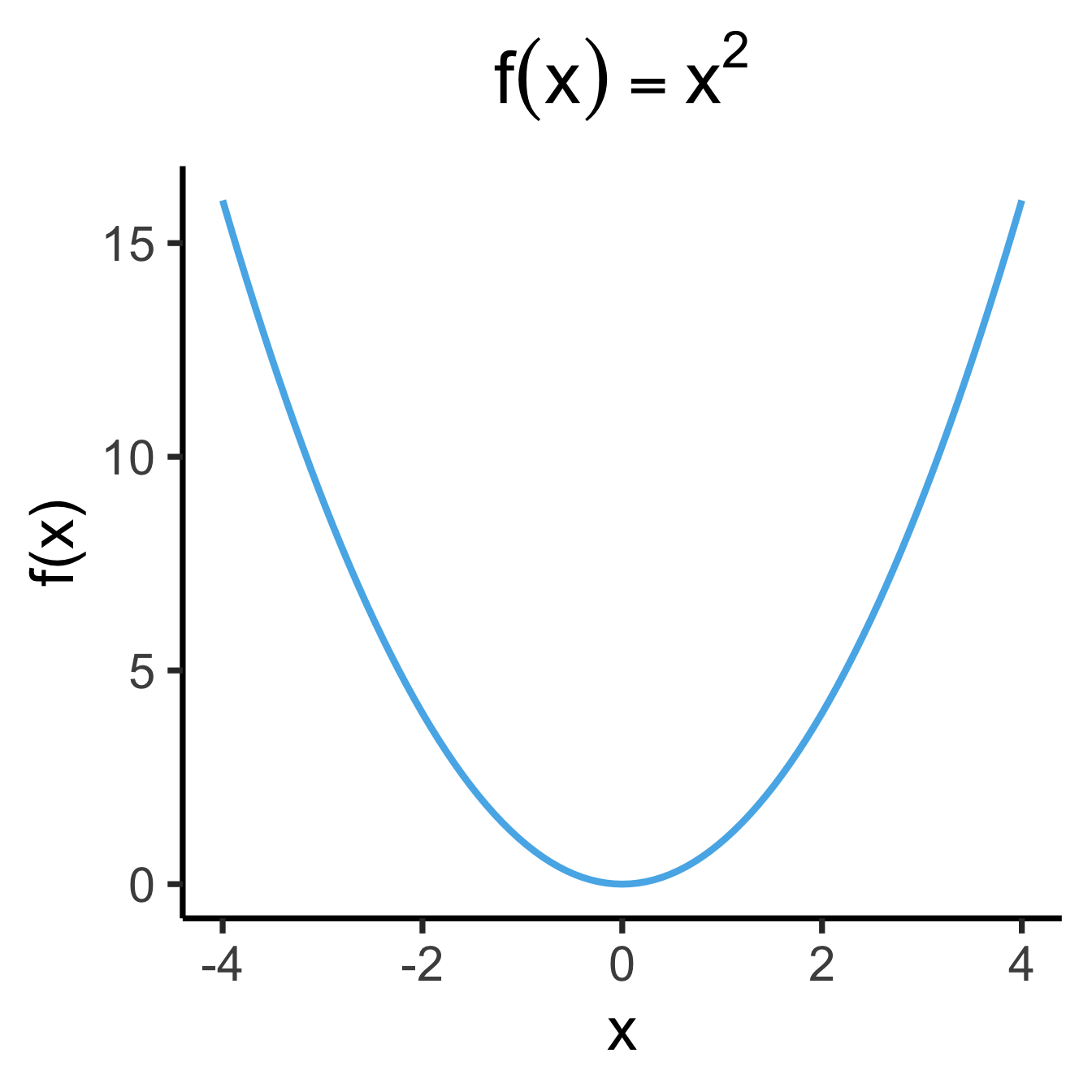
x2_label <- TeX("$f(x) = x^2$")
ggplot(data.frame(x=c(-4,4)), aes(x=x)) +
  stat_function(
    fun =~ .x^2,
    linewidth = g_linewidth * 1.5,
    color=cb_palette[2],
  ) +
  dsan_theme("quarter") +
  labs(
    title=x2_label,
    y="f(x)"
  )

Outliers Penalized Quadratically

  • May feel arbitrary at first (we’re “forced” to use squared error because of calculus?)
  • It also has important consequences for “learnability” via gradient descent!
Code 
library(latex2exp)
set.seed(5300)
slope <- 0.5
x_vals <- seq(from = -20, to = 20, length.out = 15)
N <- length(x_vals)
y_vals <- slope * x_vals + rnorm(N, 0, 5)
spread_vals <- y_vals - slope * x_vals
sim_lg_df <- tibble(
  x = x_vals, y = y_vals, spread = spread_vals
)
abs_sum <- round(sum(abs(sim_lg_df$spread)), 3)
abs_label <- TeX(paste0("$\\Sigma = ",abs_sum,"$"))
sim_lg_df |> ggplot(aes(x=x, y=y)) +
  geom_point(size=g_pointsize * 0.9) +
  geom_abline(
    slope=slope,
    intercept=0,
    linetype="dashed",
    color='black',
    linewidth=g_linewidth
  ) +
  geom_segment(
    aes(xend=x, yend=slope * x),
    arrow=arrow(
      angle=90,
      length=unit(0.125,'inches'),
      ends='both'
    ),
    linewidth=1.5*g_linewidth,
    color=cb_palette[7],
    alpha=0.9,
  ) +
  ylim(-15, 15) +
  xlim(-20, 27.5) +
  coord_equal() +
  theme_dsan(base_size=28) +
  labs(title="Absolute Penalties") +
  geom_text(
    data=data.frame(x=15, y=-10), label=abs_label,
    size=12
  )
sq_sum <- round(sum((sim_lg_df$spread)^2), 3)
sq_label <- TeX(paste0("$\\Sigma = ",sq_sum,"$"))
sim_lg_df |> ggplot(aes(x=x, y=y)) +
  geom_point(size=g_pointsize * 0.9) +
  geom_abline(
    slope=slope,
    intercept=0,
    linetype="dashed",
    color='black',
    linewidth=g_linewidth
  ) +
  geom_rect(
    aes(
      xmin=x,
      xmax=x+abs(spread),
      ymin=ifelse(spread < 0, y, y - spread),
      ymax=ifelse(spread < 0, y - spread, y)
    ),
    color='black',
    fill=cb_palette[7],
    alpha=0.2,
  ) +
  ylim(-15, 15) +
  xlim(-20, 27.5) +
  coord_equal() +
  theme_dsan(base_size=30) +
  labs(title="Squared Penalties") +
  geom_text(
    data=data.frame(x=15, y=-10), label=sq_label,
    size=12
  )
Warning in is.na(x): is.na() applied to non-(list or vector) of type
'expression'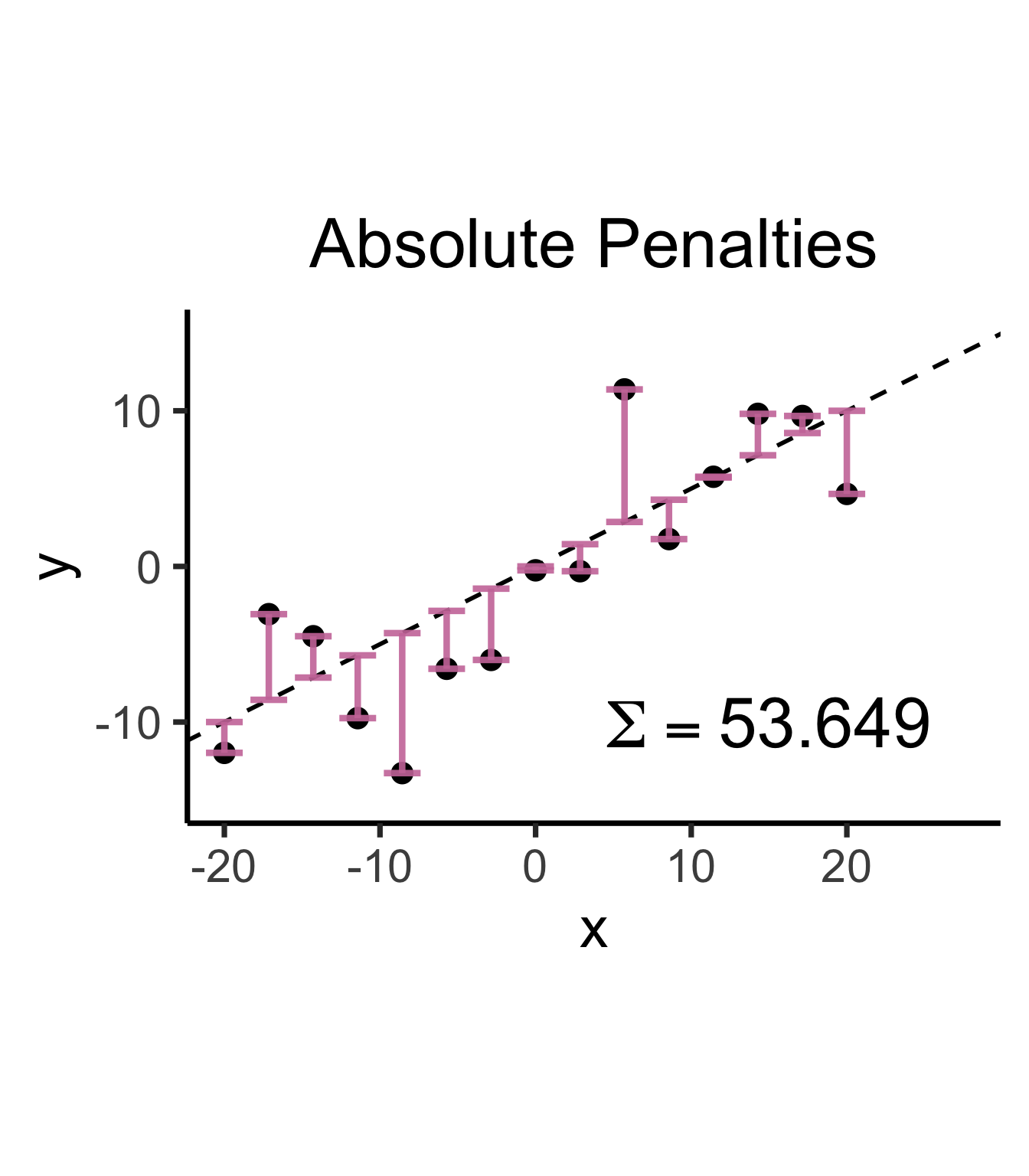

Warning in is.na(x): is.na() applied to non-(list or vector) of type
'expression'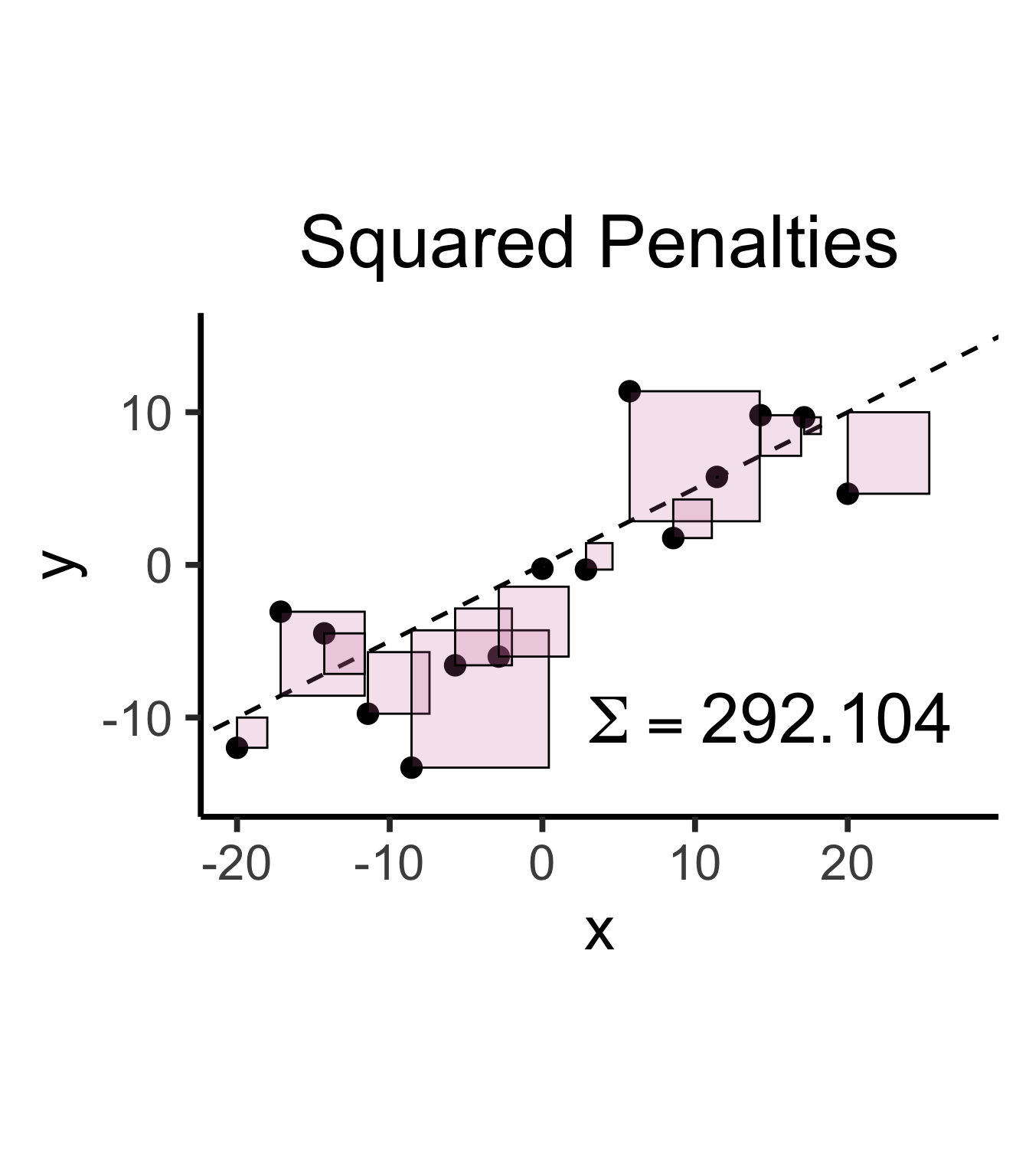

Key Features of Regression Line

  • Regression line is BLUE: Best Linear Unbiased Estimator
  • What exactly is it the “best” linear estimator of?

\[ \widehat{y} = \underbrace{\widehat{\beta}_0}_{\mathclap{\small\begin{array}{c}\text{Estimated} \\[-5mm] \text{intercept}\end{array}}} ~+~ \underbrace{\widehat{\beta}_1}_{\mathclap{\small\begin{array}{c}\text{Estimated} \\[-4mm] \text{slope}\end{array}}}\cdot x \]

is chosen so that

\[ \widehat{\theta} = \left(\widehat{\beta}_0, \widehat{\beta}_1\right) = \argmin_{\beta_0, \beta_1}\left[ \sum_{x_i \in X} \left(~~\overbrace{\widehat{y}(x_i)}^{\mathclap{\small\text{Predicted }y}} - \overbrace{\expect{Y \mid X = x_i}}^{\small \text{Avg. }y\text{ when }x = x_i}\right)^{2~} \right] \]

Where Did That \(\mathbb{E}[Y \mid X = x_i]\) Come From?

  • From our assumption that the irreducible errors \(\varepsilon_i\) are normally distributed \(\mathcal{N}(0, \sigma^2)\)

Image Source
  • Kind of an immensely important point, since it gives us a hint for checking whether model assumptions hold: spread around the regression line should be \(\mathcal{N}(0, \sigma^2)\)

Heteroskedasticity

  • If spread increases or decreases for larger \(x\), for example, then \(\varepsilon \nsim \mathcal{N}(0, \sigma^2)\)

Figure 3.11 from James et al. (2023)

But… What About Other Types of Vars?

  • 5000: you saw nominal, ordinal, cardinal vars
  • 5100: you wrestled with discrete vs. continuous RVs
  • Good News #1: Regression can handle all these types+more!
  • Good News #2: Distinctions between classification and regression diminish as you learn fancier regression methods!
    • tldr: Predict continuous probabilities \(\Pr(Y) \in [0,1]\) (regression), then guess 1 if \(\Pr(Y) > 0.5\) (classification)
  • By end of 5300 you should have something on your toolbelt for handling most cases like “I want to do [regression / classification], but my data is [not cardinal+continuous]”

Quiz Review

Objective Functions

“Fitting” a statistical model to data means minimizing some loss function that measures “how bad” our predictions are:

NoteOptimization Problems: General Form

Find \(x^*\), the solution to

\[ \begin{align} \min_{x} ~ & f(x) &\text{(Objective function)} \\ \text{s.t. } ~ & g(x) = 0 &\text{(Constraints)} \end{align} \]

  • Earlier we were able to write \(x^* = \argmax_x{f(x)}\), since there were no constraints. Is there a way to write a formula like this with constraints?
  • Answer: Yes! Thx Giuseppe-Luigi Lagrangia = Joseph-Louis Lagrange:

\[ x^* = \argmax_{x,~\lambda}f(x) - \lambda[g(x)] \]

(Why worry about constraints when OLS is unconstrained? …Soon we’ll need to penalize complexity!)

Example Problem

NoteExample 1: Unconstrained Optimization

Find \(x^*\), the solution to

\[ \begin{align} \min_{x} ~ & f(x) = 3x^2 - x \\ \text{s.t. } ~ & \varnothing \end{align} \]

TipOur Plan
  • Compute the derivative \(f'(x) = \frac{\partial}{\partial x}f(x)\),
  • Set it equal to zero: \(f'(x) = 0\), and
  • Solve this equality for \(x\), i.e., find values \(x^*\) satisfying \(f'(x^*) = 0\)

Computing the derivative:

\[ f'(x) = \frac{\partial}{\partial x}f(x) = \frac{\partial}{\partial x}\left[3x^2 - x\right] = 6x - 1, \]

Solving for \(x^*\), the value(s) satisfying \(\frac{\partial}{\partial x}f'(x^*) = 0\) for just-derived \(f'(x)\):

\[ f'(x^*) = 0 \iff 6x^* - 1 = 0 \iff x^* = \frac{1}{6}. \]

Derivative Cheatsheet

Type of Thing Thing Change in Thing when \(x\) Changes by Tiny Amount
Polynomial \(f(x) = x^n\) \(f'(x) = \frac{\partial}{\partial x}f(x) = nx^{n-1}\)
Fraction \(f(x) = \frac{1}{x}\) Use Polynomial rule (since \(\frac{1}{x} = x^{-1}\)) to get \(f'(x) = -\frac{1}{x^2}\)
Logarithm \(f(x) = \ln(x)\) \(f'(x) = \frac{\partial}{\partial x} = \frac{1}{x}\)
Exponential \(f(x) = e^x\) \(f'(x) = \frac{\partial}{\partial x}e^x = e^x\) (🧐❗️)
Multiplication \(f(x) = g(x)h(x)\) \(f'(x) = g'(x)h(x) + g(x)h'(x)\)
Division \(f(x) = \frac{g(x)}{h(x)}\) Too hard to memorize… turn it into Multiplication, as \(f(x) = g(x)(h(x))^{-1}\)
Composition (Chain Rule) \(f(x) = g(h(x))\) \(f'(x) = g'(h(x))h'(x)\)
Fancy Logarithm \(f(x) = \ln(g(x))\) \(f'(x) = \frac{g'(x)}{g(x)}\) by Chain Rule
Fancy Exponential \(f(x) = e^{g(x)}\) \(f'(x) = g'(x)e^{g(x)}\) by Chain Rule

References

Gelman, Andrew, and Jennifer Hill. 2007. Data Analysis Using Regression and Multilevel/Hierarchical Models. Cambridge University Press. https://www.dropbox.com/scl/fi/asbumi3g0gqa4xl9va7wp/Andrew-Gelman-Jennifer-Hill-Data-Analysis-Using-Regression-and-Multilevel_Hierarchical-Models.pdf?rlkey=zf8icjhm7rswvxrpm7d10m65o&dl=1.
James, Gareth, Daniela Witten, Trevor Hastie, Robert Tibshirani, and Jonathan Taylor. 2023. An Introduction to Statistical Learning: With Applications in Python. Springer Nature. https://books.google.com?id=ygzJEAAAQBAJ.