Code
source("../dsan-globals/_globals.r")
set.seed(5300)Week 3: Getting Fancy with Regression
DSAN 5300: Statistical Learning
Spring 2025, Georgetown University
Class Sessions
Recap Linear Regression
What happens to my dependent variable \(Y\) when my independent variable \(X\) changes by 1 unit?
Whenever you carry out a regression, keep the goal in the front of your mind:
\[ \DeclareMathOperator*{\argmax}{argmax} \DeclareMathOperator*{\argmin}{argmin} \newcommand{\bigexp}[1]{\exp\mkern-4mu\left[ #1 \right]} \newcommand{\bigexpect}[1]{\mathbb{E}\mkern-4mu \left[ #1 \right]} \newcommand{\definedas}{\overset{\small\text{def}}{=}} \newcommand{\definedalign}{\overset{\phantom{\text{defn}}}{=}} \newcommand{\eqeventual}{\overset{\text{eventually}}{=}} \newcommand{\Err}{\text{Err}} \newcommand{\expect}[1]{\mathbb{E}[#1]} \newcommand{\expectsq}[1]{\mathbb{E}^2[#1]} \newcommand{\fw}[1]{\texttt{#1}} \newcommand{\given}{\mid} \newcommand{\green}[1]{\color{green}{#1}} \newcommand{\heads}{\outcome{heads}} \newcommand{\iid}{\overset{\text{\small{iid}}}{\sim}} \newcommand{\lik}{\mathcal{L}} \newcommand{\loglik}{\ell} \DeclareMathOperator*{\maximize}{maximize} \DeclareMathOperator*{\minimize}{minimize} \newcommand{\mle}{\textsf{ML}} \newcommand{\nimplies}{\;\not\!\!\!\!\implies} \newcommand{\orange}[1]{\color{orange}{#1}} \newcommand{\outcome}[1]{\textsf{#1}} \newcommand{\param}[1]{{\color{purple} #1}} \newcommand{\pgsamplespace}{\{\green{1},\green{2},\green{3},\purp{4},\purp{5},\purp{6}\}} \newcommand{\prob}[1]{P\left( #1 \right)} \newcommand{\purp}[1]{\color{purple}{#1}} \newcommand{\sign}{\text{Sign}} \newcommand{\spacecap}{\; \cap \;} \newcommand{\spacewedge}{\; \wedge \;} \newcommand{\tails}{\outcome{tails}} \newcommand{\Var}[1]{\text{Var}[#1]} \newcommand{\bigVar}[1]{\text{Var}\mkern-4mu \left[ #1 \right]} \]
What Regression is Not
Final reminder that Regression, PCA have different goals!
If your goal was to, e.g., generate realistic \((x,y)\) pairs, then (mathematically) you want PCA! Roughly:
\[ \widehat{f}_{\text{PCA}} = \min_{\mathbf{c}}\left[ \sum_{i=1}^{n} (\widehat{x}_i(\mathbf{c}) - x_i)^2 + (\widehat{y}_i(\mathbf{c}) - y_i)^2 \right] \]
Our goal is a good predictor of \(Y\):
\[ \widehat{f}_{\text{Reg}} = \min_{\beta_0, \beta_1}\left[ \sum_{i=1}^{n} (\widehat{y}_i(\beta) - y_i)^2 \right] \]
How Do We Define “Best”?
- Intuitively, two different ways to measure how well a line fits the data:
Code
library(tidyverse)
set.seed(5321)
N <- 11
x <- seq(from = 0, to = 1, by = 1 / (N - 1))
y <- x + rnorm(N, 0, 0.2)
mean_y <- mean(y)
spread <- y - mean_y
df <- tibble(x = x, y = y, spread = spread)
ggplot(df, aes(x=x, y=y)) +
geom_abline(slope=1, intercept=0, linetype="dashed", color=cbPalette[1], linewidth=g_linewidth*2) +
geom_segment(xend=(x+y)/2, yend=(x+y)/2, linewidth=g_linewidth*2, color=cbPalette[2]) +
geom_point(size=g_pointsize) +
coord_equal() +
xlim(0, 1) + ylim(0, 1) +
dsan_theme("half") +
labs(
title = "Principal Component Line"
)
ggplot(df, aes(x=x, y=y)) +
geom_abline(slope=1, intercept=0, linetype="dashed", color=cbPalette[1], linewidth=g_linewidth*2) +
geom_segment(xend=x, yend=x, linewidth=g_linewidth*2, color=cbPalette[2]) +
geom_point(size=g_pointsize) +
coord_equal() +
xlim(0, 1) + ylim(0, 1) +
dsan_theme("half") +
labs(
title = "Regression Line"
)Warning: Removed 1 row containing missing values or values outside the scale range
(`geom_segment()`).Warning: Removed 1 row containing missing values or values outside the scale range
(`geom_point()`).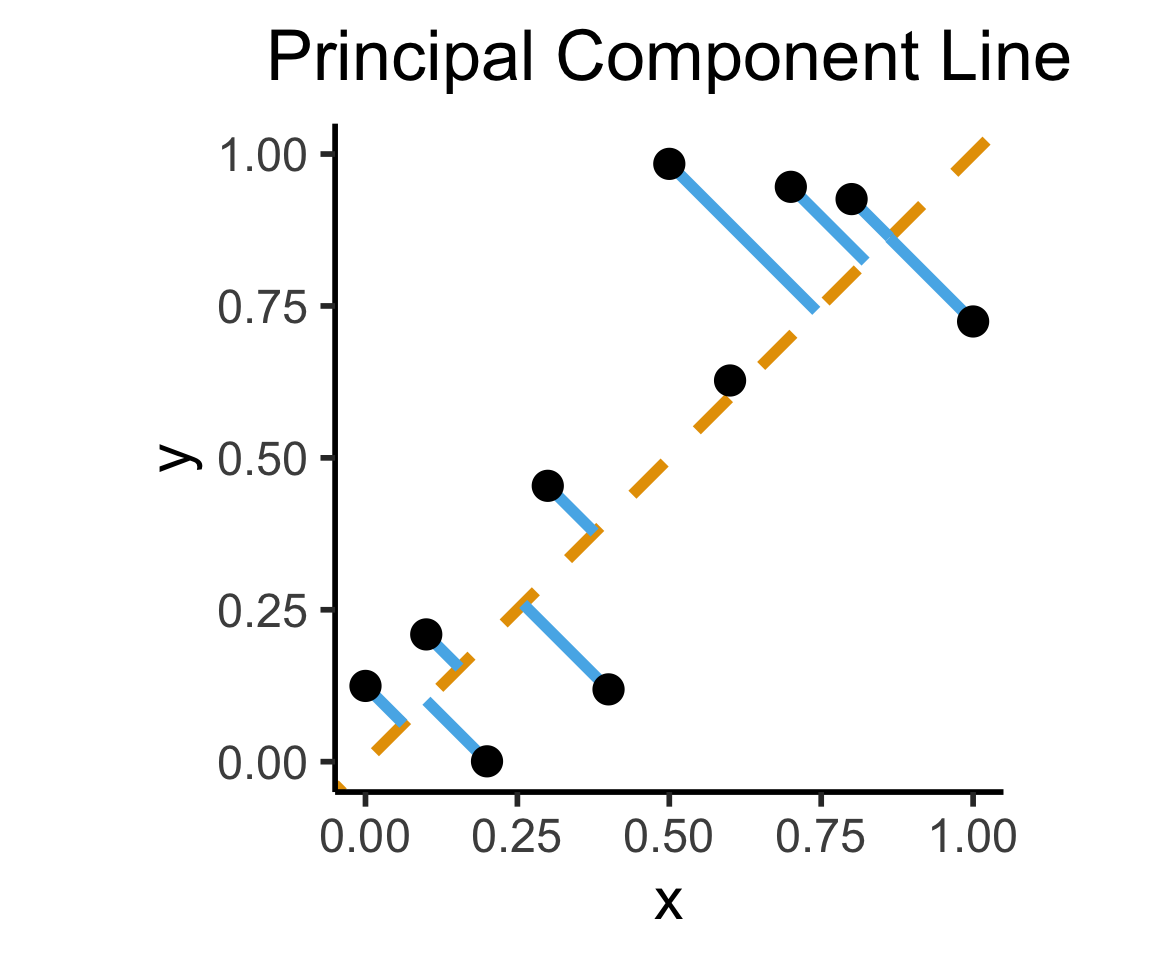
Warning: Removed 1 row containing missing values or values outside the scale range
(`geom_segment()`).Warning: Removed 1 row containing missing values or values outside the scale range
(`geom_point()`).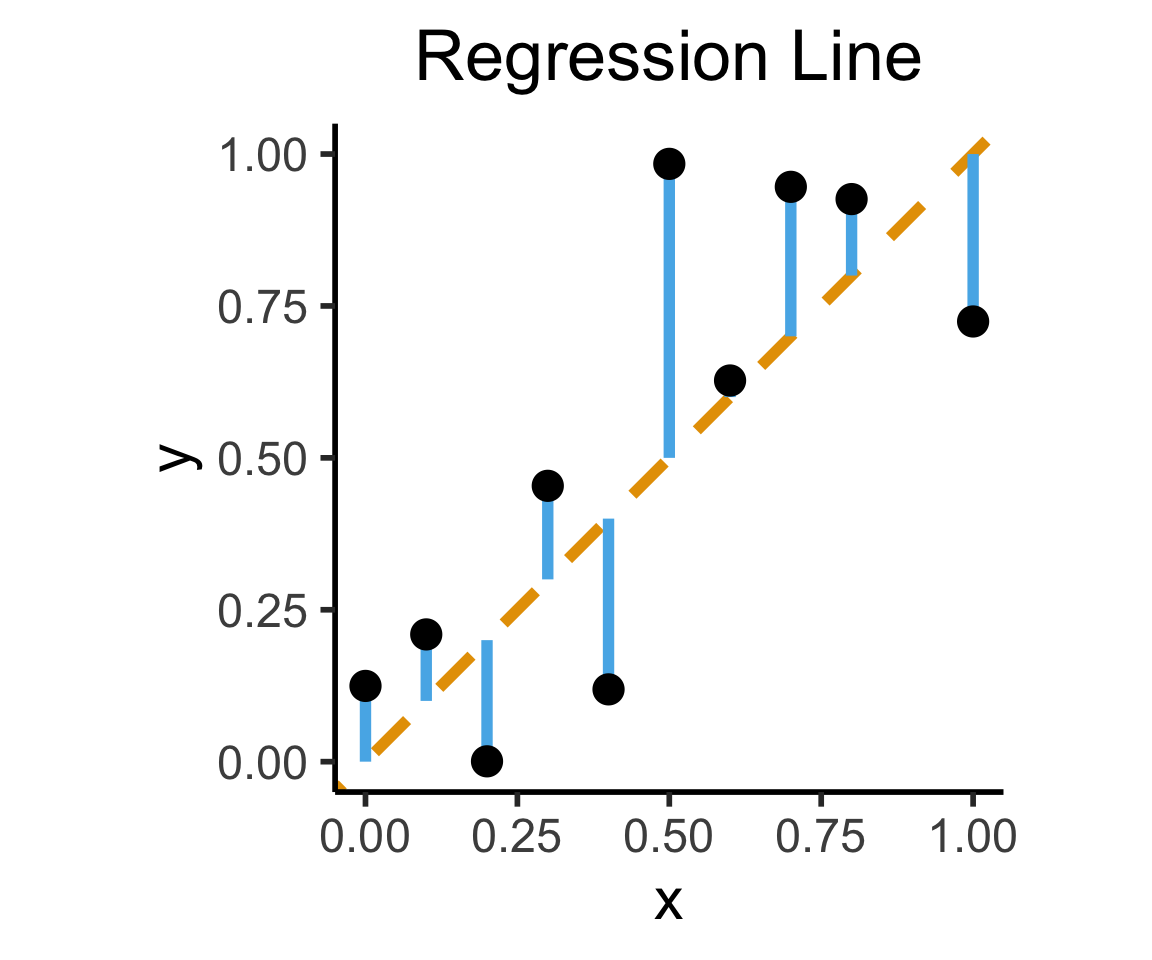
On the difference between these two lines, and why it matters, I cannot recommend Gelman and Hill (2007) enough!
Multiple Linear Regression (MLR)
Multiple Linear Regression (MLR) Model
- Notation: \(x_{i,j}\) = value of independent variable \(j\) for person/observation \(i\)
- \(M\) = total number of independent variables
\[ \widehat{y}_i = \beta_0 + \beta_1x_{i,1} + \beta_2x_{i,2} + \cdots + \beta_M x_{i,M} \]
- \(\beta_j\) interpretation: a one-unit increase in \(x_{i,j}\) is associated with a \(\beta_j\) unit increase in \(y_i\), holding all other independent variables constant
Visualizing Multiple Linear Regression
Interpreting MLR
Code
mlr_model = smf.ols(
formula="sales ~ TV + radio + newspaper",
data=ad_df
)
mlr_result = mlr_model.fit()
print(mlr_result.summary().tables[1])==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 2.9389 0.312 9.422 0.000 2.324 3.554
TV 0.0458 0.001 32.809 0.000 0.043 0.049
radio 0.1885 0.009 21.893 0.000 0.172 0.206
newspaper -0.0010 0.006 -0.177 0.860 -0.013 0.011
==============================================================================- Holding
radioandnewspaperspending constant…- An increase of $1K in spending on
TVadvertising is associated with - An increase in sales of about 46 units
- An increase of $1K in spending on
- Holding
TVandnewspaperspending constant…- An increase of $1K in spending on
radioadvertising is associated with - An increase in sales of about 189 units
- An increase of $1K in spending on
But Wait…
Code
# print(mlr_result.summary2(float_format='%.3f'))
print(mlr_result.summary2()) Results: Ordinary least squares
=================================================================
Model: OLS Adj. R-squared: 0.896
Dependent Variable: sales AIC: 780.3622
Date: 2025-03-09 05:24 BIC: 793.5555
No. Observations: 200 Log-Likelihood: -386.18
Df Model: 3 F-statistic: 570.3
Df Residuals: 196 Prob (F-statistic): 1.58e-96
R-squared: 0.897 Scale: 2.8409
------------------------------------------------------------------
Coef. Std.Err. t P>|t| [0.025 0.975]
------------------------------------------------------------------
Intercept 2.9389 0.3119 9.4223 0.0000 2.3238 3.5540
TV 0.0458 0.0014 32.8086 0.0000 0.0430 0.0485
radio 0.1885 0.0086 21.8935 0.0000 0.1715 0.2055
newspaper -0.0010 0.0059 -0.1767 0.8599 -0.0126 0.0105
-----------------------------------------------------------------
Omnibus: 60.414 Durbin-Watson: 2.084
Prob(Omnibus): 0.000 Jarque-Bera (JB): 151.241
Skew: -1.327 Prob(JB): 0.000
Kurtosis: 6.332 Condition No.: 454
=================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the
errors is correctly specified.Code
slr_model = smf.ols(
formula="sales ~ newspaper",
data=ad_df
)
slr_result = slr_model.fit()
print(slr_result.summary2()) Results: Ordinary least squares
==================================================================
Model: OLS Adj. R-squared: 0.047
Dependent Variable: sales AIC: 1220.6714
Date: 2025-03-09 05:24 BIC: 1227.2680
No. Observations: 200 Log-Likelihood: -608.34
Df Model: 1 F-statistic: 10.89
Df Residuals: 198 Prob (F-statistic): 0.00115
R-squared: 0.052 Scale: 25.933
-------------------------------------------------------------------
Coef. Std.Err. t P>|t| [0.025 0.975]
-------------------------------------------------------------------
Intercept 12.3514 0.6214 19.8761 0.0000 11.1260 13.5769
newspaper 0.0547 0.0166 3.2996 0.0011 0.0220 0.0874
------------------------------------------------------------------
Omnibus: 6.231 Durbin-Watson: 1.983
Prob(Omnibus): 0.044 Jarque-Bera (JB): 5.483
Skew: 0.330 Prob(JB): 0.064
Kurtosis: 2.527 Condition No.: 65
==================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the
errors is correctly specified.- MLR results can be drastically different from SLR results, because of correlations (next slide)
- This is a good thing! It’s how we’re able to control for confounding variables!
Correlations Among Features
Code
ad_df.drop(columns="id").corr() TV radio newspaper sales
TV 1.000000 0.054809 0.056648 0.782224
radio 0.054809 1.000000 0.354104 0.576223
newspaper 0.056648 0.354104 1.000000 0.228299
sales 0.782224 0.576223 0.228299 1.000000- Observe how \(\text{cor}(\texttt{radio}, \texttt{newspaper}) \approx 0.35\)
- In markets where we spend more on
radioour sales will tend to be higher… - Corr matrix \(\implies\) we spend more on
newspaperin those same markets… - In SLR which only examines
salesvs.newspaper, we (correctly!) observe that higher values ofnewspaperare associated with higher values ofsales… - In essence,
newspaperadvertising is a surrogate forradioadvertising \(\implies\) in our SLR,newspaper“gets credit” for the association betweenradioandsales
Another MLR Superpower: Incorporating Categorical Vars
\[ \begin{align*} Y &= \beta_0 + \beta_1 \times \texttt{income} \\ &\phantom{Y} \end{align*} \]
Code
credit_df <- read_csv("assets/Credit.csv")Rows: 400 Columns: 11
── Column specification ────────────────────────────────────────────────────────
Delimiter: ","
chr (4): Own, Student, Married, Region
dbl (7): Income, Limit, Rating, Cards, Age, Education, Balance
ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.Code
credit_plot <- credit_df |> ggplot(aes(x=Income, y=Balance)) +
geom_point(size=0.5*g_pointsize) +
geom_smooth(method='lm', formula="y ~ x", linewidth=1) +
theme_dsan() +
labs(
title="Credit Card Balance vs. Income Level",
x="Income ($1K)",
y="Credit Card Balance ($)"
)
credit_plot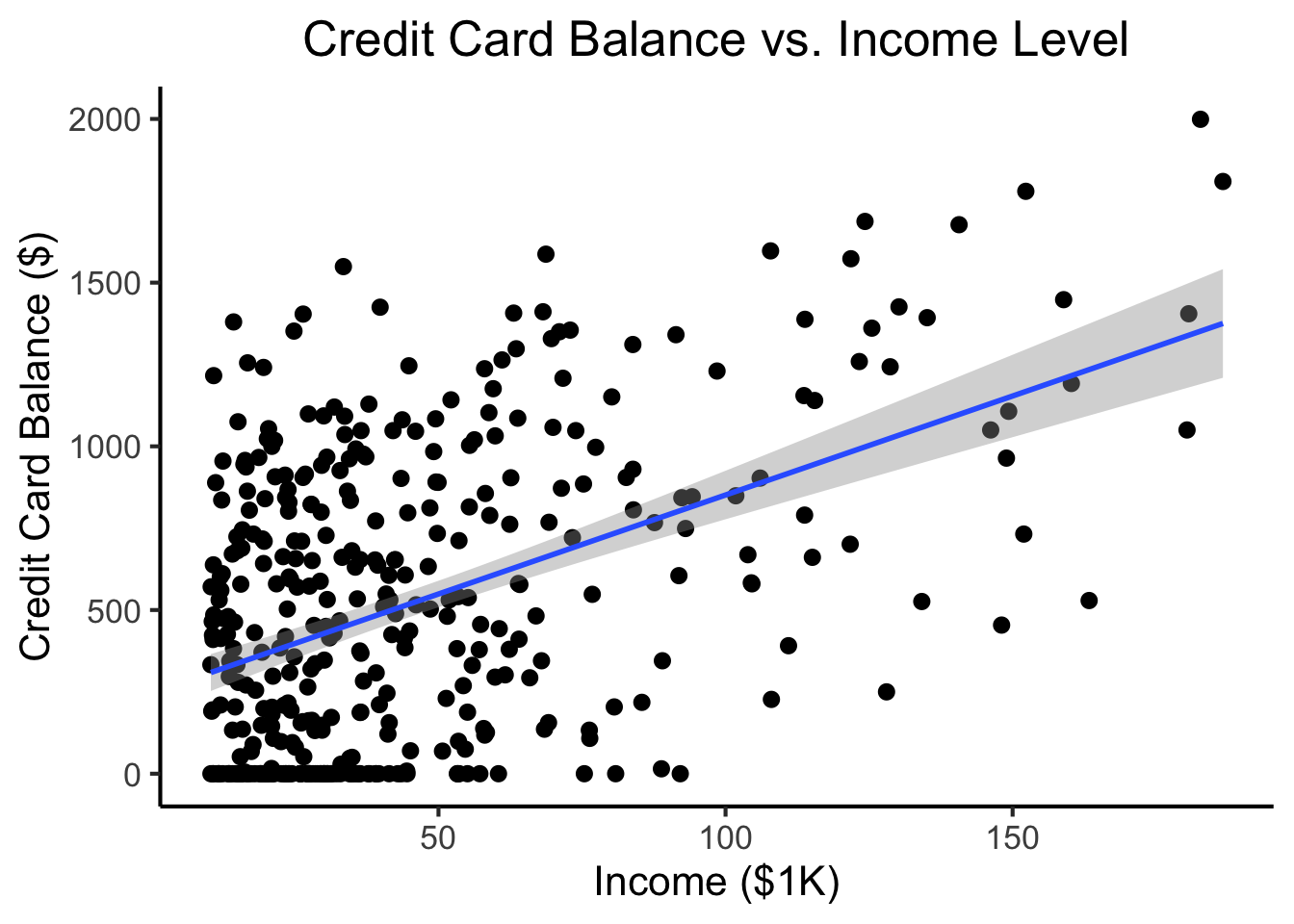
\[ \begin{align*} Y = &\beta_0 + \beta_1 \times \texttt{income} + \beta_2 \times \texttt{Student} \\ &+ \beta_3 \times (\texttt{Student} \times \texttt{Income}) \end{align*} \]
Code
student_plot <- credit_df |> ggplot(aes(x=Income, y=Balance, color=Student)) +
geom_point(size=0.5*g_pointsize) +
geom_smooth(method='lm', formula="y ~ x", linewidth=1) +
theme_dsan() +
labs(
title="Credit Card Balance vs. Income Level",
x="Income ($1K)",
y="Credit Card Balance ($)"
)
student_plot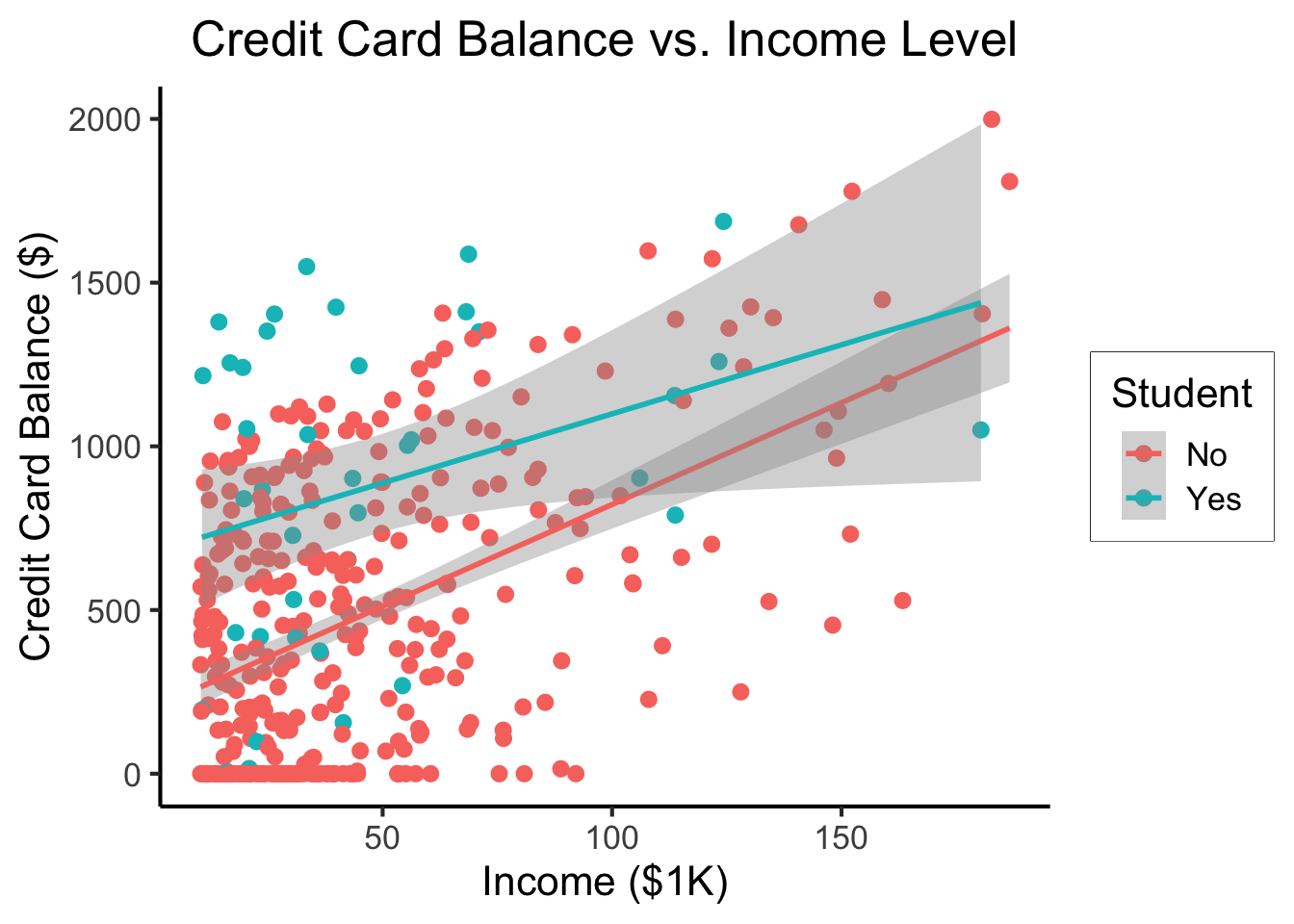
- Why do we need the \(\texttt{Student} \times \texttt{Income}\) term?
- Understanding this setup will open up a vast array of possibilities for regression 😎
- (Dear future Jeff, let’s go through this on the board! Sincerely, past Jeff)
Logistic Regression
From MLR to Logistic Regression
- As DSAN students, you know that we’re still sweeping classification under the rug!
- We saw how to include binary/multiclass covariates, but what if the actual thing we’re trying to predict is binary?
- The wrong approach is the “Linear Probability Model”:
\[ \Pr(Y \mid X) = \beta_0 + \beta_1 X + \varepsilon \]
Credit Default
Code
library(tidyverse)
library(ggExtra)
default_df <- read_csv("assets/Default.csv") |>
mutate(default_num = ifelse(default=="Yes",1,0))Rows: 10000 Columns: 4
── Column specification ────────────────────────────────────────────────────────
Delimiter: ","
chr (2): default, student
dbl (2): balance, income
ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.Code
default_plot <- default_df |> ggplot(aes(x=balance, y=income, color=default, shape=default)) +
geom_point(alpha=0.6) +
theme_classic(base_size=16) +
labs(
title="Credit Defaults by Income and Account Balance",
x = "Account Balance",
y = "Income"
)
default_mplot <- default_plot |> ggMarginal(type="boxplot", groupColour=FALSE, groupFill=TRUE)
default_mplot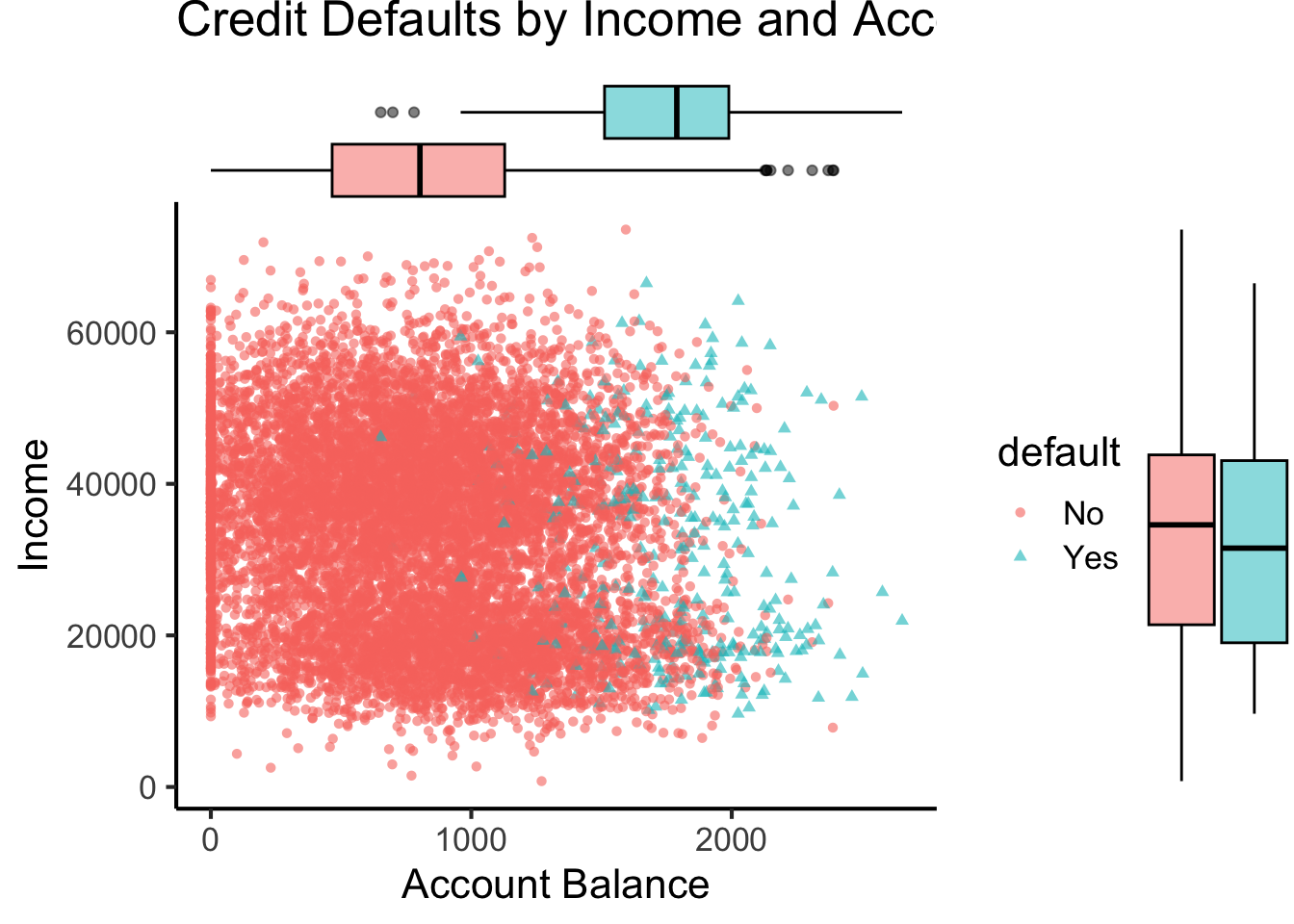
Lines vs. Sigmoids(!)
Here’s what lines look like for this dataset:
Code
#lpm_model <- lm(default ~ balance, data=default_df)
default_df |> ggplot(
aes(
x=balance, y=default_num
)
) +
geom_point(aes(color=default)) +
stat_smooth(method="lm", formula=y~x, color='black') +
theme_classic(base_size=16)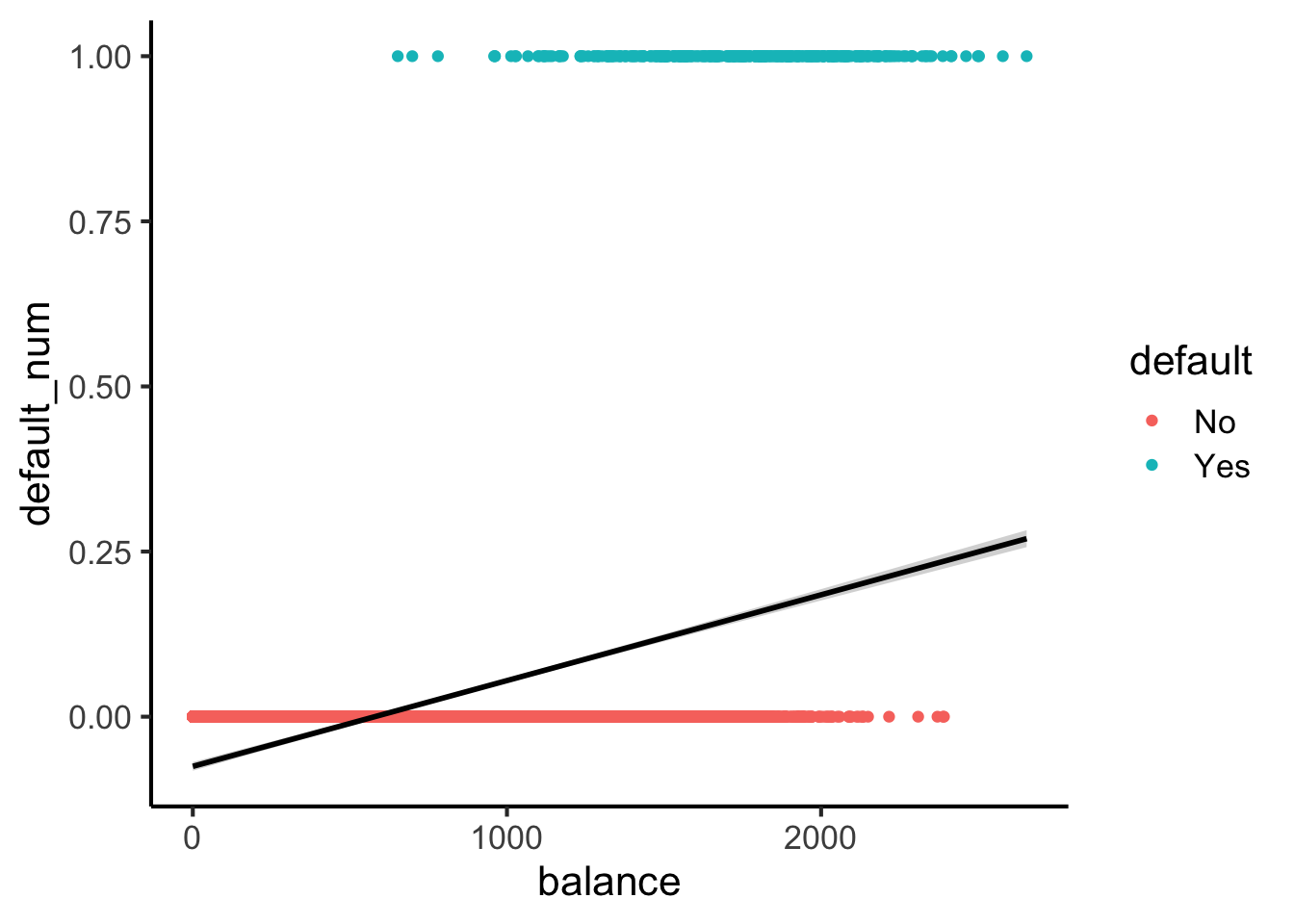
Here’s what sigmoids look like:
Code
library(tidyverse)
logistic_model <- glm(default_num ~ balance, family=binomial(link='logit'),data=default_df)
default_df$predictions <- predict(logistic_model, newdata = default_df, type = "response")
my_sigmoid <- function(x) 1 / (1+exp(-x))
default_df |> ggplot(aes(x=balance, y=default_num)) +
#stat_function(fun=my_sigmoid) +
geom_point(aes(color=default)) +
geom_line(
data=default_df,
aes(x=balance, y=predictions),
linewidth=1
) +
theme_classic(base_size=16)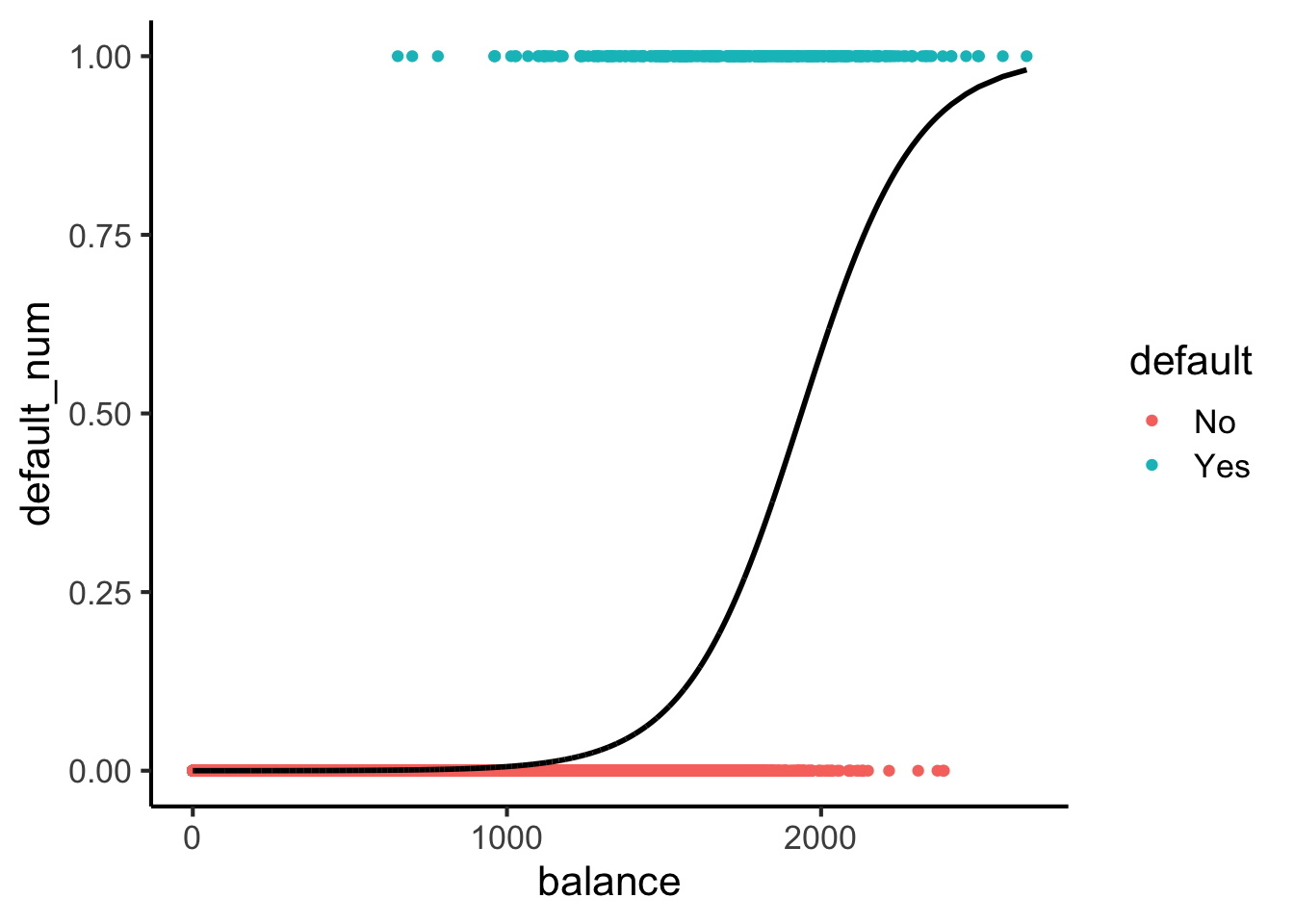
\[ \Pr(Y \mid X) = \beta_0 + \beta_1 X + \varepsilon \]
\[ \log\underbrace{\left[ \frac{\Pr(Y \mid X)}{1 - \Pr(Y \mid X)} \right]}_{\mathclap{\smash{\text{Odds Ratio}}}} = \beta_0 + \beta_1 X + \varepsilon \]
But Let’s Derive This!
\[ \begin{align*} \Pr(Y \mid X) &= \frac{e^{\beta_0 + \beta_1X}}{1 + e^{\beta_0 + \beta_1X}} \\ \iff \underbrace{\frac{\Pr(Y \mid X)}{1 - \Pr(Y \mid X)}}_{\text{Odds Ratio}} &= e^{\beta_0 + \beta_1X} \\ \iff \underbrace{\log\left[ \frac{\Pr(Y \mid X)}{1 - \Pr(Y \mid X)} \right]}_{\text{Log-Odds Ratio}} &= \beta_0 + \beta_1X \end{align*} \]
Now How Will We Ever Find “Good” Parameter Values?
- If only we had some sort of estimator… One that would choose \(\beta_0\) and \(\beta_1\) so as to maximize the likelihood of seeing some data…
\[ L(\beta_0, \beta_1) = \prod_{\{i \mid y_i = 1\}}\Pr(Y = 1 \mid X) \prod_{\{i \mid y_i = 0\}}(1-\Pr(Y = 1 \mid X)) \]
- (Much more on this later 😸)
The Interpretation Problem
Code
options(scipen = 999)
print(summary(logistic_model))
Call:
glm(formula = default_num ~ balance, family = binomial(link = "logit"),
data = default_df)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -10.6513306 0.3611574 -29.49 <0.0000000000000002 ***
balance 0.0054989 0.0002204 24.95 <0.0000000000000002 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 2920.6 on 9999 degrees of freedom
Residual deviance: 1596.5 on 9998 degrees of freedom
AIC: 1600.5
Number of Fisher Scoring iterations: 8- Slope is no longer the same everywhere! It varies across different values of \(x\)…
- Let’s brainstorm some possible ways to make our lives easier when interpreting these coefficients!
References
Gelman, Andrew, and Jennifer Hill. 2007. Data Analysis Using Regression and Multilevel/Hierarchical Models. Cambridge University Press.
Appendix: MLR in R
Code
library(tidyverse)
ad_df <- read_csv("assets/Advertising.csv") |> rename(id=`...1`)New names:
Rows: 200 Columns: 5
── Column specification
──────────────────────────────────────────────────────── Delimiter: "," dbl
(5): ...1, TV, radio, newspaper, sales
ℹ Use `spec()` to retrieve the full column specification for this data. ℹ
Specify the column types or set `show_col_types = FALSE` to quiet this message.
• `` -> `...1`Code
mlr_model <- lm(
sales ~ TV + radio + newspaper,
data=ad_df
)
print(summary(mlr_model))
Call:
lm(formula = sales ~ TV + radio + newspaper, data = ad_df)
Residuals:
Min 1Q Median 3Q Max
-8.8277 -0.8908 0.2418 1.1893 2.8292
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2.938889 0.311908 9.422 <0.0000000000000002 ***
TV 0.045765 0.001395 32.809 <0.0000000000000002 ***
radio 0.188530 0.008611 21.893 <0.0000000000000002 ***
newspaper -0.001037 0.005871 -0.177 0.86
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.686 on 196 degrees of freedom
Multiple R-squared: 0.8972, Adjusted R-squared: 0.8956
F-statistic: 570.3 on 3 and 196 DF, p-value: < 0.00000000000000022- Holding
radioandnewspaperspending constant…- An increase of $1K in spending on
TVadvertising is associated with - An increase in sales of about 46 units
- An increase of $1K in spending on
- Holding
TVandnewspaperspending constant…- An increase of $1K in spending on
radioadvertising is associated with - An increase in sales of about 189 units
- An increase of $1K in spending on