Week 7: Spatial Data Science: Three Types of Geographic Data

PPOL 6805 / DSAN 6750: GIS for Spatial Data Science
Fall 2026

Jeff Jacobs

jj1088@georgetown.edu

Wednesday, October 7, 2026

Random Fields

\[ \text{Data} = \left\{Z(\mathbf{s}) \mid \mathbf{s} \in D \subset \mathbb{R}^2\right\} \]

\(D\) = Rectangle; \(Z(\mathbf{s})\) here: height at coordinate \(\mathbf{s} \in D\)

Key Notation / Definition

2-Dimensional Spatial Process (Schabenberger and Gotway 2004, 6)

\[ \text{Data} = \left\{Z(\mathbf{s}) \mid \mathbf{s} \in D \subset \mathbb{R}^d\right\} \]

Geostatistical Data Lattice/Region Data Point Pattern
Criteria Fixed \(D\), Continuous Fixed \(D\), Discrete Random subset \(D^* \subseteq D\)
What's Random? Value of \(Z\) at POINT \(\mathbf{s}_i \in D\) Value of \(Z\) across POLYGON \(\mathbf{r}_i \subseteq D\) Subset \(D^*\) formed by events
Interest Infer non-observed parts of \(D\) Autocorrelation, clustering Point-generating process
Example

Dumping sand on a table: \(D = \{(x,y) \mid x \in [0,2], y \in [0,1]\}\)

  • \(Z(\mathbf{s}_i)\): Attribute(s) at site \(\mathbf{s}_i\) (\(\mathbf{s}_i = (x_i,y_i)\))
  • \(Z(\mathbf{s}_i)\) example: Height of sand. \(Z(\mathbf{s}_1) = 500\text{m}\), \(Z(\mathbf{s}_2) = 850\text{m}\), \(\ldots\)

\(Z(\mathbf{s})\) observed over \(N \times N\) grid of plots of land

  • Well-defined ‘Neighbors’ (next section!)
  • Autocorrelation: Are points around \(\mathbf{s}_i\) likely to have values similar to \(Z(\mathbf{s}_i)\)?

Unknown number of lightning strikes \(\mathbf{s}_1, \mathbf{s}_2, \ldots\)

  • All of \(D\) is observed, but what determines subset \(D^*\) where events occur?
  • Unmarked: Locations only
  • Marked: Locations+info (e.g., intensity of strike)

Geostatistical Data: Dumping Sand onto a Table!

  • Domain \(D\): tabletop; Random process: dumping sand onto the tabletop
  • \(\Omega\): All possible realizations of process. \(\omega_i \in \Omega\) Particular realization
Figure 1: \(\omega_1 \in \Omega\)
Figure 2: \(\omega_2 \in \Omega\)
Figure 3: \(\omega_3 \in \Omega\)
Figure 4: \(\omega_4 \in \Omega\)

Example: Water Coverage in Bhola, Bangladesh

Parenti (2011)

Geostatistical Modeling: Terrains Are Not Spiky Chaotic Landscapes!

(If they were… we’d have to worry about suddenly plunging 1000km with each step!)

Geostatistical Data \(\rightarrow\) Point Pattern

(Example “event”: Discovery of a point higher than Washington Monument)

Indicator function: \(\mathbb{1}\left[Z(\mathbf{s}) > 860\text{m}\right]\)

Code 
set.seed(6805)
library(tidyverse)
library(sf)
library(terra)
library(latex2exp)
#### Define area
lat_range <- c(-5.0, -6.0)
lon_range <- c(15, 20)
#lon_center <- -5.4
#lat_center <- 36.75
# And the window around this centroid
lat_radius <- 0.05
lon_radius <- 0.1

gen_random_table <- function(world_num=1, return_data=FALSE, rand_seed=NULL) {
  if (!is.null(rand_seed)) {
    set.seed(rand_seed)
  } else {
    rand_seed <- sample(1:9999, size=1)
    set.seed(rand_seed)
  }
  lat_center <- runif(1, min=min(lat_range), max=max(lat_range))
  lon_center <- runif(1, min=min(lon_range), max=max(lon_range))
  lon_lower <- lon_center - lon_radius
  lon_upper <- lon_center + lon_radius
  lat_lower <- lat_center - lat_radius
  lat_upper <- lat_center + lat_radius
  coords <- data.frame(x = c(lon_lower, lon_lower, lon_upper, lon_upper),
                       y = c(lat_lower, lat_upper, lat_lower, lat_upper))
  coords_sf <- st_as_sf(coords, coords = c("x", "y"), crs = 4326)
  # Using geodata
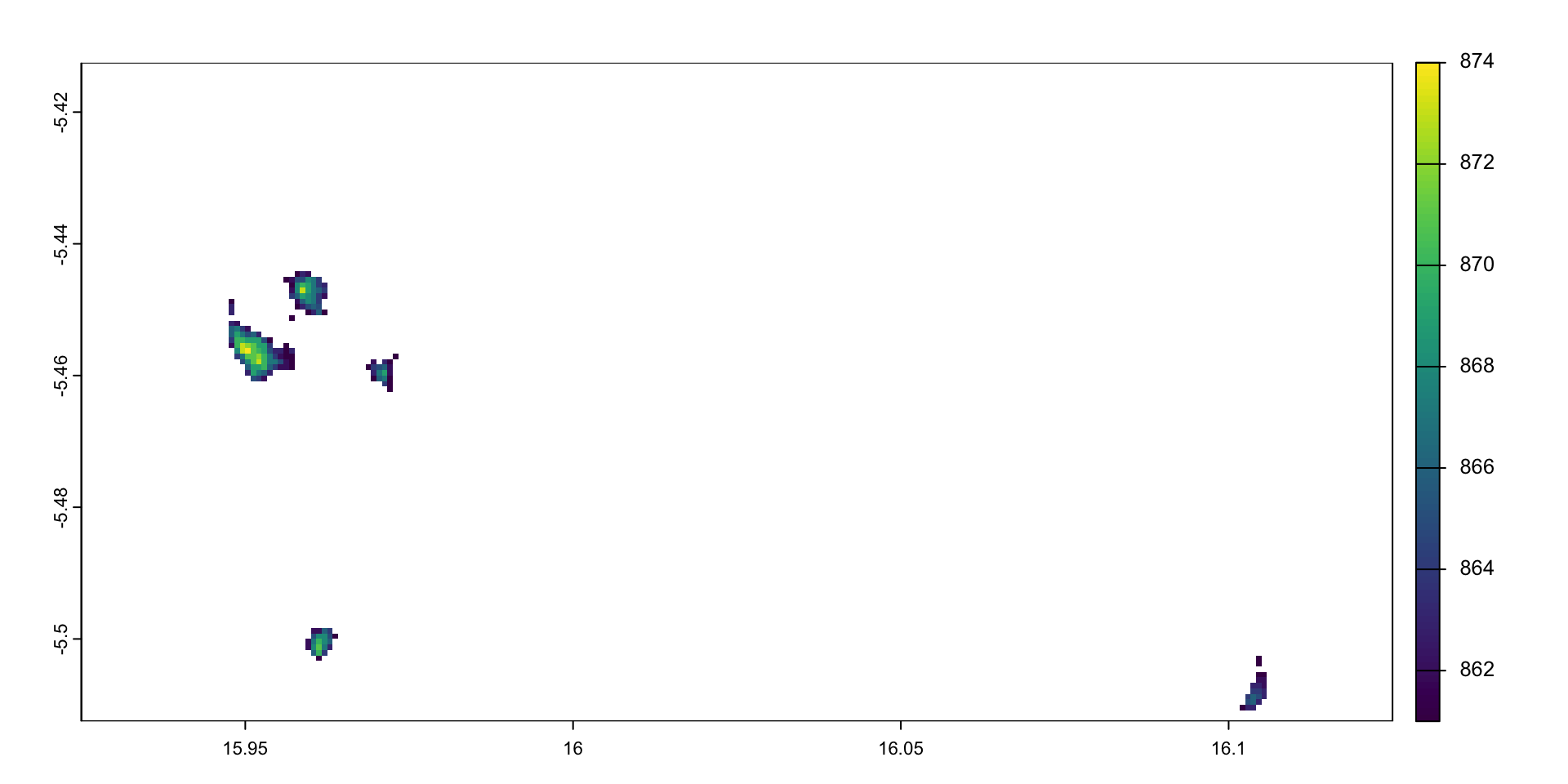
  elev <- geodata::elevation_3s(lon = lon_center, lat = lat_center, res=2.5, path = getwd())
  elev <- terra::crop(elev, coords_sf)
  return(elev)
}

compute_hillshade <- function(elev) {
  # Calculate hillshade
  slopes <- terra::terrain(elev, "slope", unit = "radians")
  aspect <- terra::terrain(elev, "aspect", unit = "radians")
  hs <- terra::shade(slopes, aspect)
  return(hs)
}

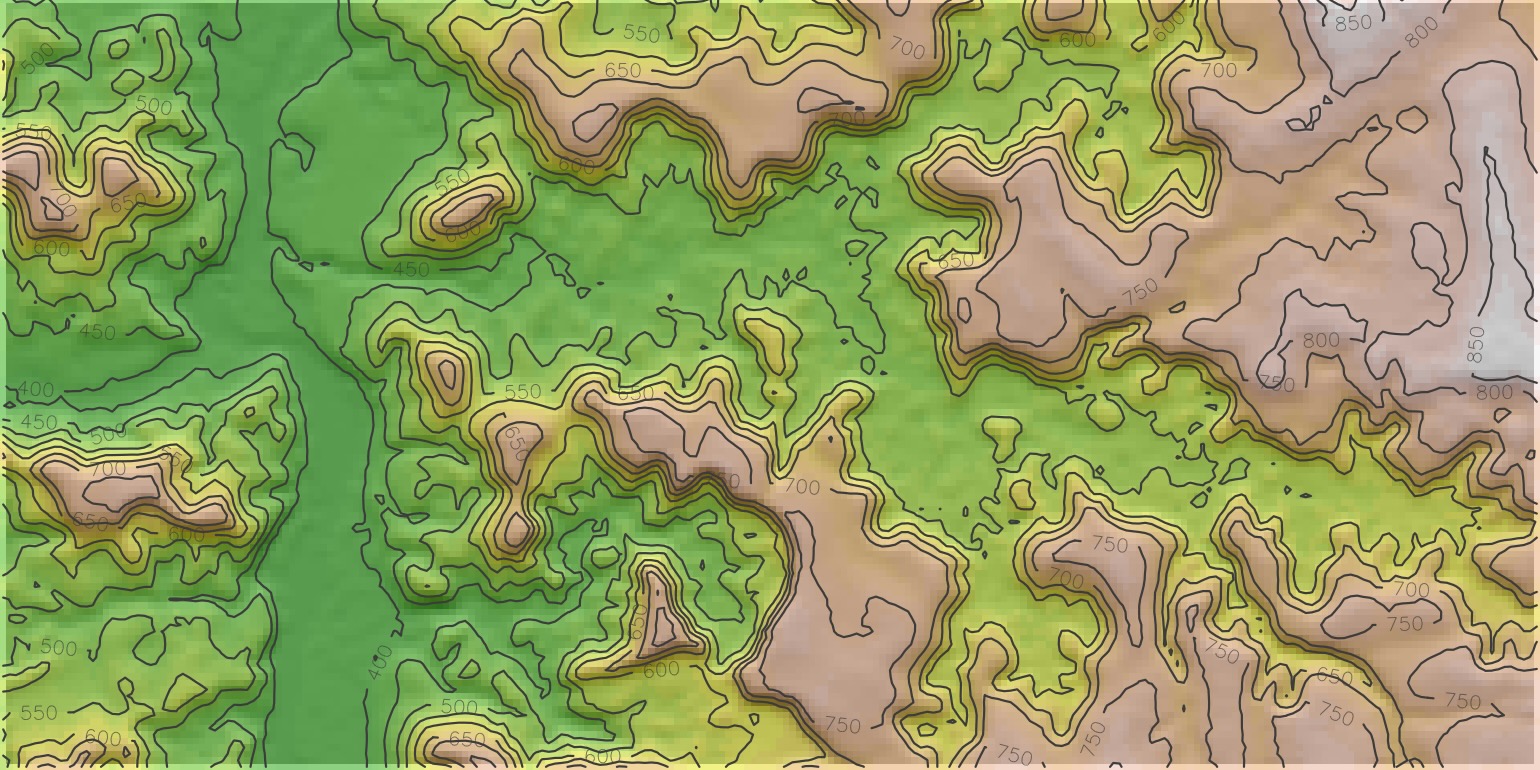
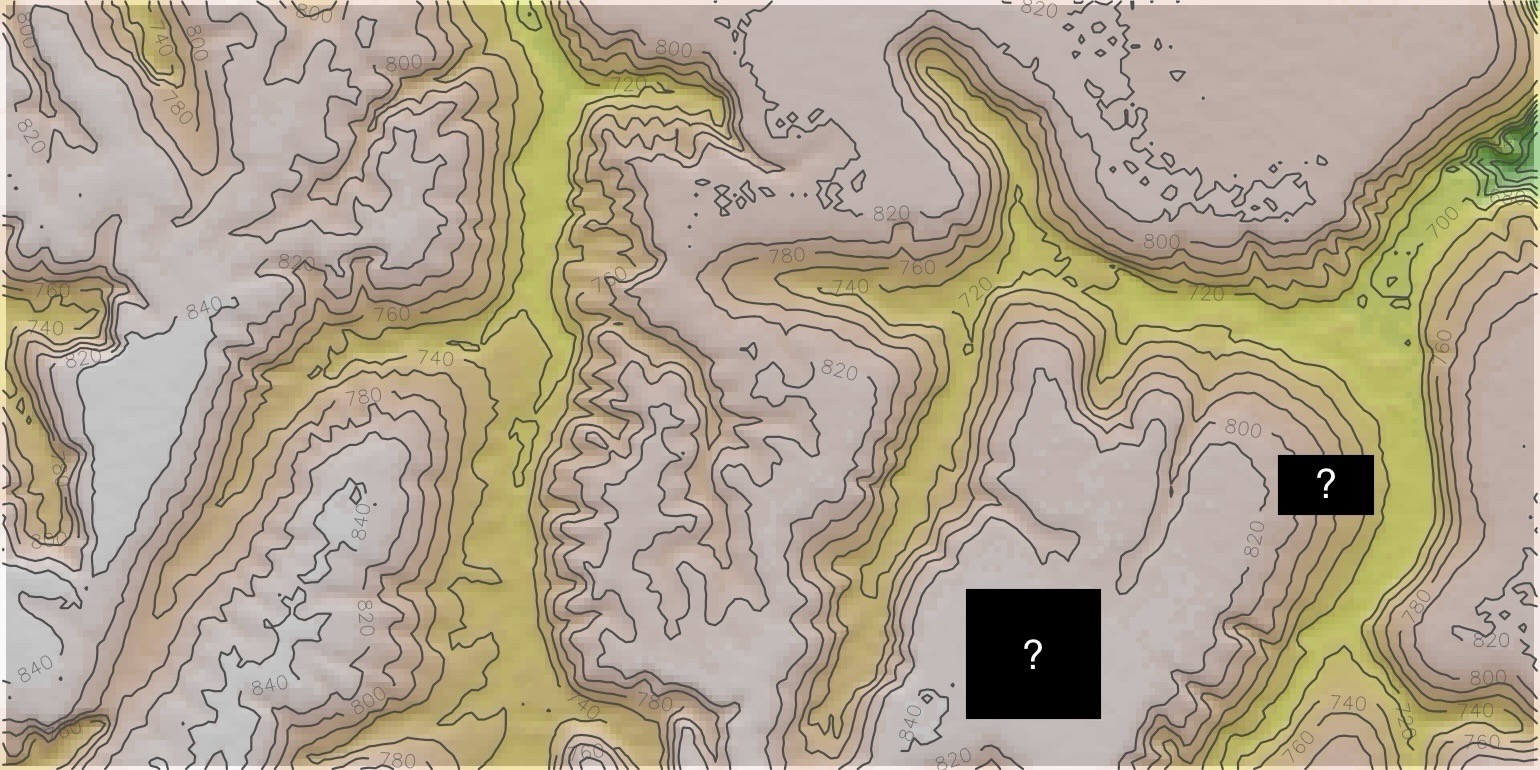
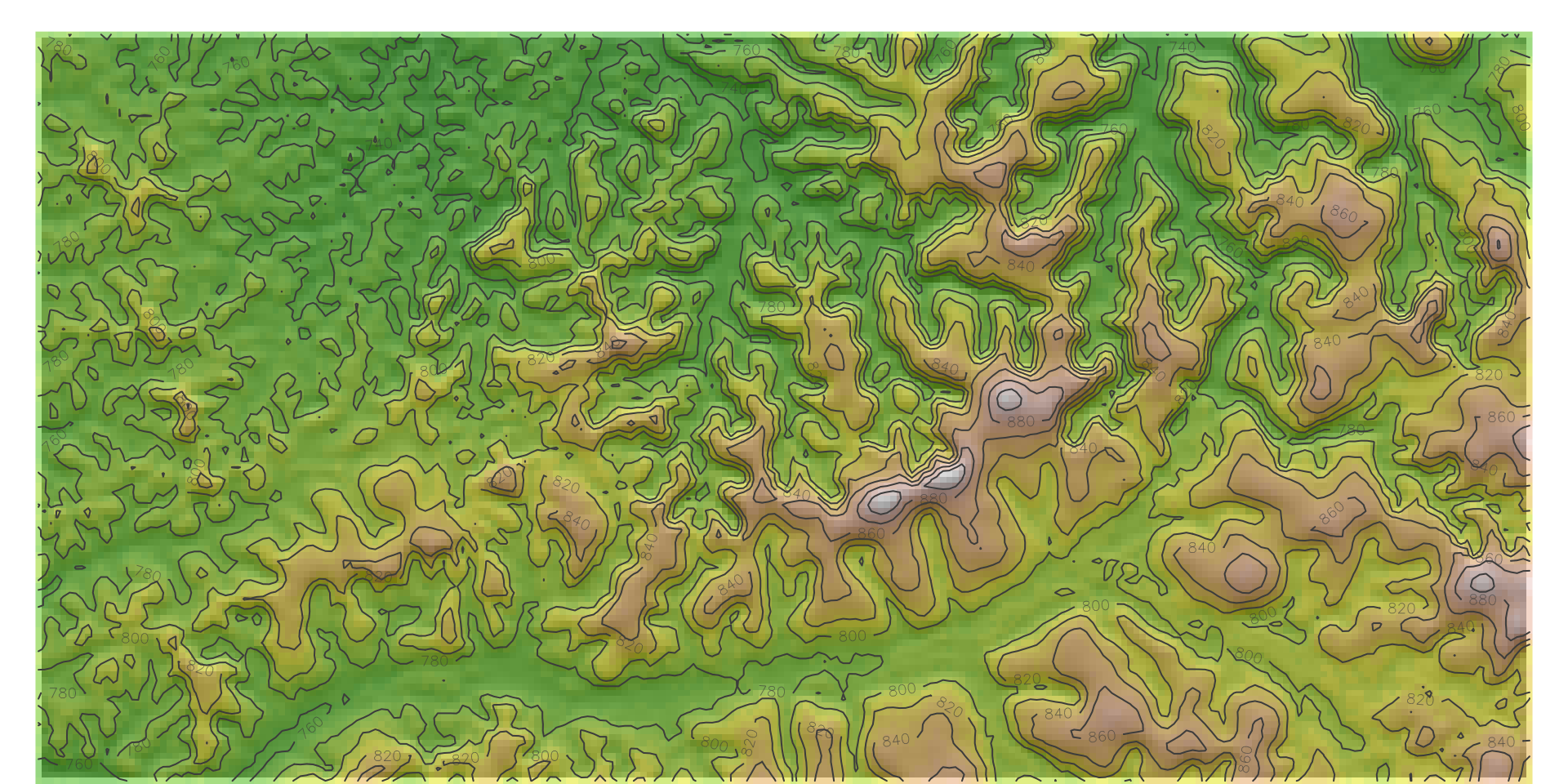
plot_hillshade <- function(elev, hs, title=NULL) {
  ## Plot hillshading as basemap
  # (here using terra::plot, but could use tmap)
  # lat_upper_trimmed <- lat_upper - 0.001*lat_upper
  # lat_lower_trimmed <- lat_lower - 0.001*lat_lower
  base_plot <- terra::plot(
    hs, col = gray(0:100 / 100), legend = FALSE, axes = FALSE, mar=c(0,0,1,0), grid=TRUE
  )
  #    xlim = c(elev_xmin, elev_xmax), ylim = c(elev_ymin, elev_ymax))
  # overlay with elevation
  
  color_vec <- terrain.colors(25)
  plot(elev, col = color_vec, alpha = 0.5, legend = FALSE, axes = FALSE, add = TRUE)
  
  # add contour lines
  terra::contour(elev, col = "grey30", add = TRUE)
  if (!is.null(title)) {
    world_name <- TeX(sprintf(r"(World $\omega_{%d} \in \Omega$)", world_num))
    title(world_name)
  }
}
elev_r1 <- gen_random_table(rand_seed=6810)
hs_r1 <- compute_hillshade(elev_r1)
plot_hillshade(elev_r1, hs_r1)

Code 
terra::ifel(elev_r1 > 860, elev_r1, NA) |> plot()

Code 
elev_r2 <- gen_random_table(rand_seed=6815)
hs_r2 <- compute_hillshade(elev_r2)
plot_hillshade(elev_r2, hs_r2)

Code 
my_quant <- function(x) quantile(x, 0.99)
elev_99 <- terra::global(elev_r2, my_quant)[1,1]
elev_indic_r2 <- terra::ifel(
  elev_r2 > elev_99, elev_r2, NA
)
plot(elev_indic_r2)

Geospatial Data \(\rightarrow\) Lattice/Region Data

Code 
table_elev <- gen_random_table(rand_seed=6805)
table_hs <- compute_hillshade(table_elev)
#plot_hillshade(table_elev, table_hs)
#par(mfrow=c(1,2), mar=c(0,0,1,1))
plot(table_elev)

(Pretend this is infinite-resolution) Infinite number of neighbors around each point!
Code 
elev_coarse <- terra::aggregate(table_elev, 12)
plot(elev_coarse)

Finite number of neighbors around each observation \(\implies\) Can study correlations between neighboring cells!

References

Parenti, Christian. 2011. Tropic of Chaos: Climate Change and the New Geography of Violence. PublicAffairs.
Schabenberger, Oliver, and Carol A. Gotway. 2004. Statistical Methods for Spatial Data Analysis. CRC Press.