| coef | std err | |
|---|---|---|
| Intercept | 19.1748 | 0.402 |
| dark_mode[T.True] | -0.4446 | 0.571 |
<Figure size 96x96 with 0 Axes>DSAN 5650: Causal Inference for Computational Social Science
Summer 2025, Georgetown University
Wednesday, July 16, 2025
Today’s Planned Schedule:
| Start | End | Topic | |
|---|---|---|---|
| Lecture | 6:30pm | 6:45pm | Final Project Tings → |
| 6:45pm | 7:20pm | Double Robustness → | |
| 7:20pm | 8:00pm | When Conditioning Won’t Cut It: IVs → | |
| Break! | 8:00pm | 8:10pm | |
| 8:10pm | 9:00pm | Drawing Causal Inferences from Text Data → |
\[ \DeclareMathOperator*{\argmax}{argmax} \DeclareMathOperator*{\argmin}{argmin} \newcommand{\bigexp}[1]{\exp\mkern-4mu\left[ #1 \right]} \newcommand{\bigexpect}[1]{\mathbb{E}\mkern-4mu \left[ #1 \right]} \newcommand{\definedas}{\overset{\small\text{def}}{=}} \newcommand{\definedalign}{\overset{\phantom{\text{defn}}}{=}} \newcommand{\eqeventual}{\overset{\text{eventually}}{=}} \newcommand{\Err}{\text{Err}} \newcommand{\expect}[1]{\mathbb{E}[#1]} \newcommand{\expectsq}[1]{\mathbb{E}^2[#1]} \newcommand{\fw}[1]{\texttt{#1}} \newcommand{\given}{\mid} \newcommand{\green}[1]{\color{green}{#1}} \newcommand{\heads}{\outcome{heads}} \newcommand{\iid}{\overset{\text{\small{iid}}}{\sim}} \newcommand{\lik}{\mathcal{L}} \newcommand{\loglik}{\ell} \DeclareMathOperator*{\maximize}{maximize} \DeclareMathOperator*{\minimize}{minimize} \newcommand{\mle}{\textsf{ML}} \newcommand{\nimplies}{\;\not\!\!\!\!\implies} \newcommand{\orange}[1]{\color{orange}{#1}} \newcommand{\outcome}[1]{\textsf{#1}} \newcommand{\param}[1]{{\color{purple} #1}} \newcommand{\pgsamplespace}{\{\green{1},\green{2},\green{3},\purp{4},\purp{5},\purp{6}\}} \newcommand{\pedge}[2]{\require{enclose}\enclose{circle}{~{#1}~} \rightarrow \; \enclose{circle}{\kern.01em {#2}~\kern.01em}} \newcommand{\pnode}[1]{\require{enclose}\enclose{circle}{\kern.1em {#1} \kern.1em}} \newcommand{\ponode}[1]{\require{enclose}\enclose{box}[background=lightgray]{{#1}}} \newcommand{\pnodesp}[1]{\require{enclose}\enclose{circle}{~{#1}~}} \newcommand{\purp}[1]{\color{purple}{#1}} \newcommand{\sign}{\text{Sign}} \newcommand{\spacecap}{\; \cap \;} \newcommand{\spacewedge}{\; \wedge \;} \newcommand{\tails}{\outcome{tails}} \newcommand{\Var}[1]{\text{Var}[#1]} \newcommand{\bigVar}[1]{\text{Var}\mkern-4mu \left[ #1 \right]} \]
With doubly-robust estimation, as long as the answer is either True or False you’re good!
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import patchworklib as pw;
import statsmodels.formula.api as smf
from causalml.match import create_table_one
from joblib import Parallel, delayed
from sklearn.linear_model import LogisticRegression
def generate_data(N=300, seed=1):
np.random.seed(seed)
# Control variables
male = np.random.binomial(1, 0.45, N)
age = np.rint(18 + np.random.beta(2, 2, N)*50)
hours = np.minimum(np.round(np.random.lognormal(5, 1.3, N), 1), 2000)
# Treatment
pr = np.maximum(0, np.minimum(1, 0.8 + 0.3*male - np.sqrt(age-18)/10))
dark_mode = np.random.binomial(1, pr, N)==1
# Outcome
read_time = np.round(np.random.normal(10 - 4*male + 2*np.log(hours) + 2*dark_mode, 4, N), 1)
# Generate the dataframe
df = pd.DataFrame({'read_time': read_time, 'dark_mode': dark_mode, 'male': male, 'age': age, 'hours': hours})
return df
user_df = generate_data(N=300)
ols_model = smf.ols("read_time ~ dark_mode", data=user_df).fit()
ols_summary = ols_model.summary()
results_as_html = ols_summary.tables[1].as_html()
ols_summary_df = pd.read_html(results_as_html, header=0, index_col=0)[0]
ols_summary_df[['coef','std err']]
#type(ols_summary.tables[1])[['coef','std err']]
# .tables[1]
# ols_df[['coef','std err']]
| coef | std err | |
|---|---|---|
| Intercept | 19.1748 | 0.402 |
| dark_mode[T.True] | -0.4446 | 0.571 |
<Figure size 96x96 with 0 Axes>(…since I couldn’t figure out how to fit it on the last slide)
Enter Uber’s causal inference library: causalml
| Control | Treatment | SMD | |
|---|---|---|---|
| Variable | |||
| n | 151 | 149 | |
| age | 46.01 (9.79) | 39.09 (11.53) | -0.6469 |
| hours | 337.78 (464.00) | 328.57 (442.12) | -0.0203 |
| male | 0.34 (0.47) | 0.66 (0.48) | 0.6732 |
And then WeightIt to generate a “love plot”:
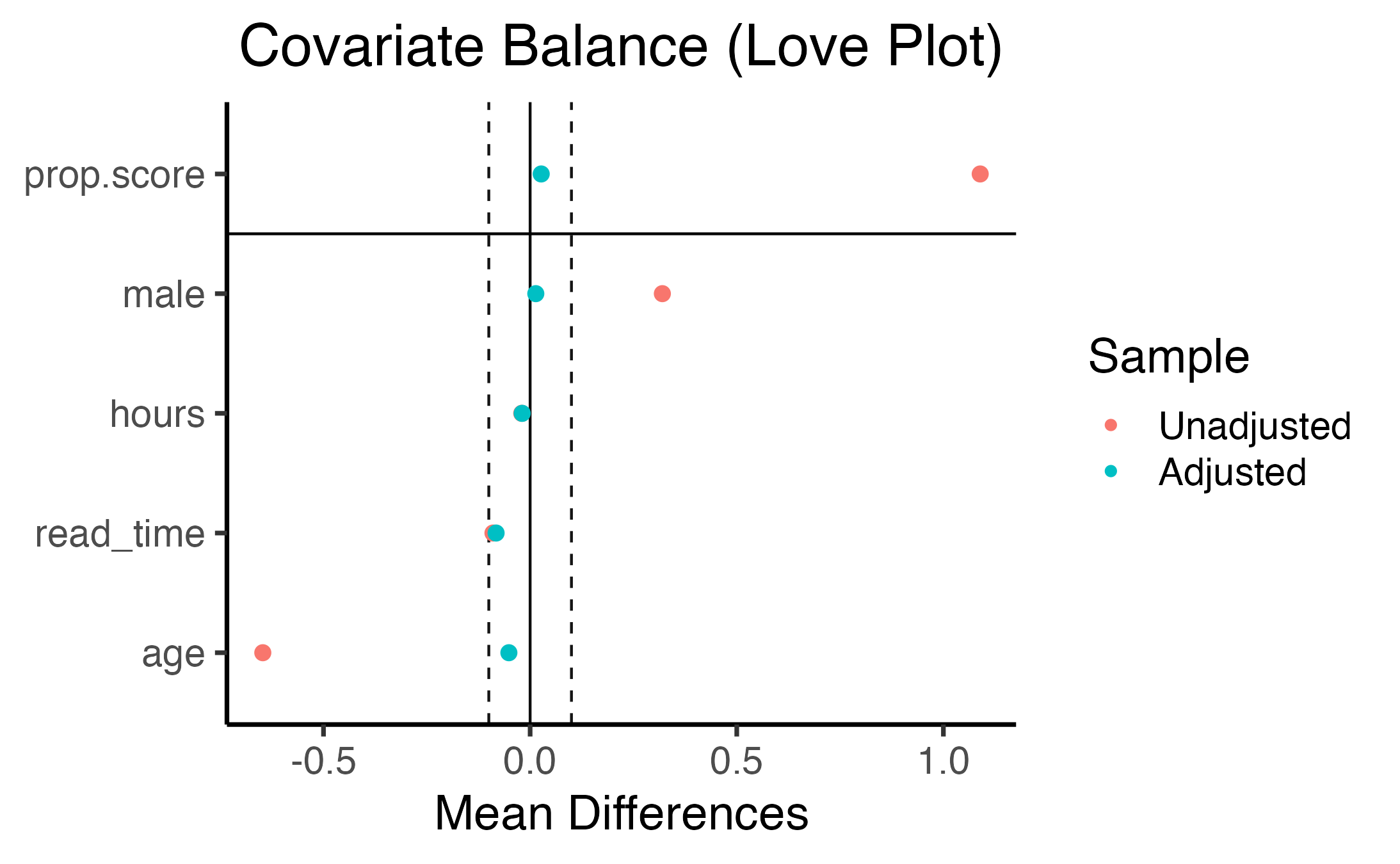
\[ \begin{align*} \hat \tau_{AIPW} &= \frac{1}{n} \sum_{i=1}^{n} \left( \text{RegEst}(X_i) + \text{PropensityAdj}(X_i, Y_i) \right) \\ \text{RegEst}(X_i) &= \hat \mu^{(1)}(X_i) - \hat \mu^{(0)}(X_i) \\ \text{PropensityAdj}(X_i, Y_i) &= \frac{D_i}{\hat{\mathtt{e}}(X_i)} \left( Y_i - \hat \mu^{(1)}(X_i) \right) - \frac{(1-D_i) }{1-\hat{\mathtt{e}}(X_i)} \left( Y_i - \hat \mu^{(0)}(X_i) \right) \end{align*} \]
where \(\mu^{(d)}(x)\) is the response function, i.e. the expected value of the outcome, conditional on observable characteristics \(x\) and treatment status \(d\), and \(e(X)\) is the propensity score.
\[ \begin{align*} \mu^{(d)}(x) &= \mathbb E \left[ Y_i \ \big | \ X_i = x, D_i = d \right] \\ \mathtt{e}(x) &= \mathbb E \left[ D_i = 1 \ \big | \ X_i = x \right] \end{align*} \]
def estimate_e(df, X, D, model_e):
e = model_e.fit(df[X], df[D]).predict_proba(df[X])[:,1]
return e
user_df['e'] = estimate_e(user_df, X, "dark_mode", LogisticRegression())
ax = pw.Brick(figsize=(7, 2.75));
sns.kdeplot(
x='e', hue='dark_mode', data=user_df,
# bins=30,
#stat='density',
common_norm=False,
fill=True,
ax=ax
);
ax.set_xlabel("$e(X)$");
ax.savefig()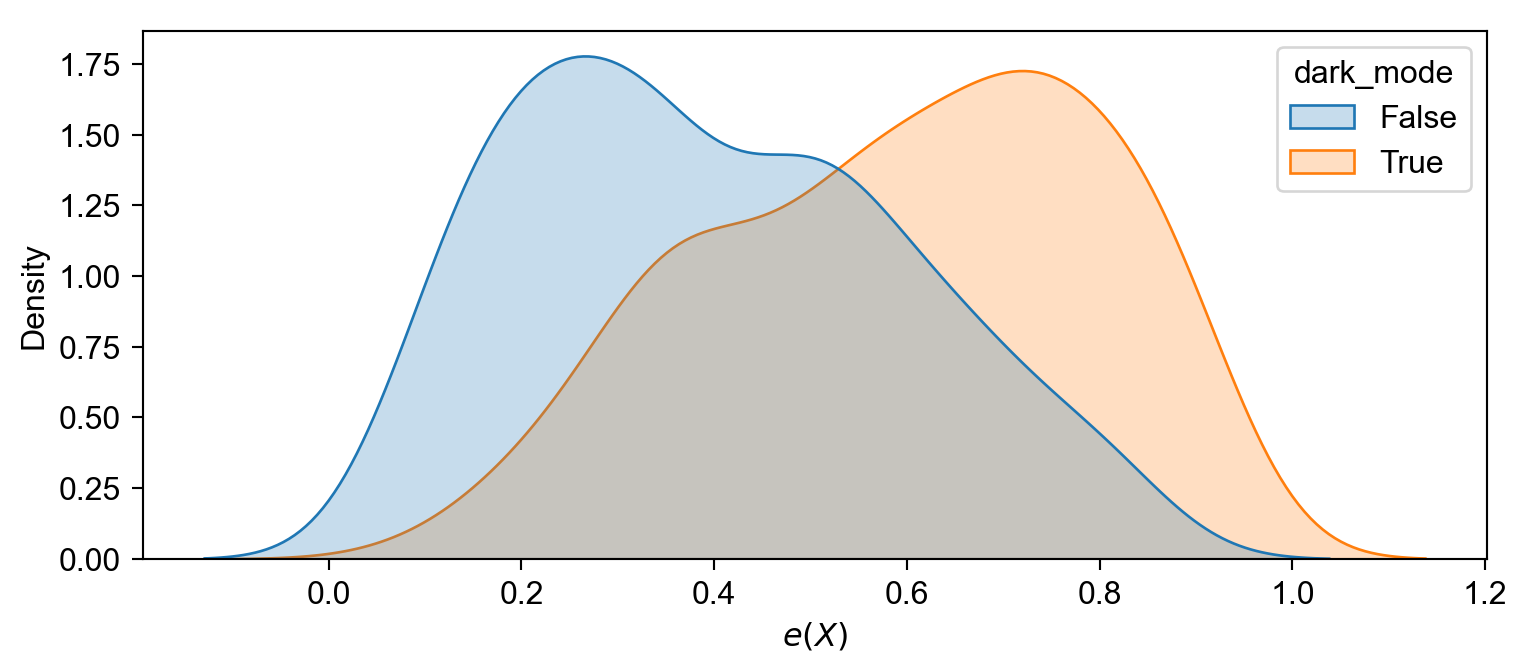
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
| Intercept | 18.5871 | 0.412 | 45.158 | 0.000 | 17.777 | 19.397 |
| dark_mode[T.True] | 1.0486 | 0.581 | 1.805 | 0.072 | -0.095 | 2.192 |
scikit-learn:def estimate_mu(df, X, D, y, model_mu):
mu = model_mu.fit(df[X + [D]], df[y])
mu0 = mu.predict(df[X + [D]].assign(dark_mode=0))
mu1 = mu.predict(df[X + [D]].assign(dark_mode=1))
return mu0, mu1
from sklearn.linear_model import LinearRegression
mu0, mu1 = estimate_mu(user_df, X, "dark_mode", "read_time", LinearRegression())
print(np.mean(mu0), np.mean(mu1))
print(np.mean(mu1-mu0))18.265714409803312 19.651524322951012
1.3858099131476969EconML, Microsoft’s “Official” ML-based econometrics library 😎from econml.dr import LinearDRLearner
model = LinearDRLearner(
model_propensity=LogisticRegression(),
model_regression=LinearRegression(),
random_state=5650
)
model.fit(Y=user_df["read_time"], T=user_df["dark_mode"], X=user_df[X]);
model.ate_inference(X=user_df[X].values, T0=0, T1=1).summary().tables[0]| mean_point | stderr_mean | zstat | pvalue | ci_mean_lower | ci_mean_upper |
| 1.321 | 0.549 | 2.409 | 0.016 | 0.246 | 2.396 |
Wrong regression model:
def compare_estimators(X_e, X_mu, D, y, seed):
df = generate_data(seed=seed)
e = estimate_e(df, X_e, D, LogisticRegression())
mu0, mu1 = estimate_mu(df, X_mu, D, y, LinearRegression())
slearn = mu1 - mu0
ipw = (df[D] / e - (1-df[D]) / (1-e)) * df[y]
aipw = slearn + df[D] / e * (df[y] - mu1) - (1-df[D]) / (1-e) * (df[y] - mu0)
return np.mean((slearn, ipw, aipw), axis=1)
def simulate_estimators(X_e, X_mu, D, y):
r = Parallel(n_jobs=8)(delayed(compare_estimators)(X_e, X_mu, D, y, i) for i in range(100))
df_tau = pd.DataFrame(r, columns=['S-learn', 'IPW', 'AIPW'])
return df_tau
# The actual plots
ax = pw.Brick(figsize=(4, 3.5))
wrong_reg_df = simulate_estimators(
X_e=['male', 'age'], X_mu=['hours'], D="dark_mode", y="read_time"
)
wrong_reg_plot = sns.boxplot(
data=pd.melt(wrong_reg_df), x='variable', y='value', hue='variable',
ax=ax,
linewidth=2
);
wrong_reg_plot.set(
title="Distribution of $\hat τ$", xlabel='', ylabel=''
);
ax.axhline(2, c='r', ls=':');
ax.savefig()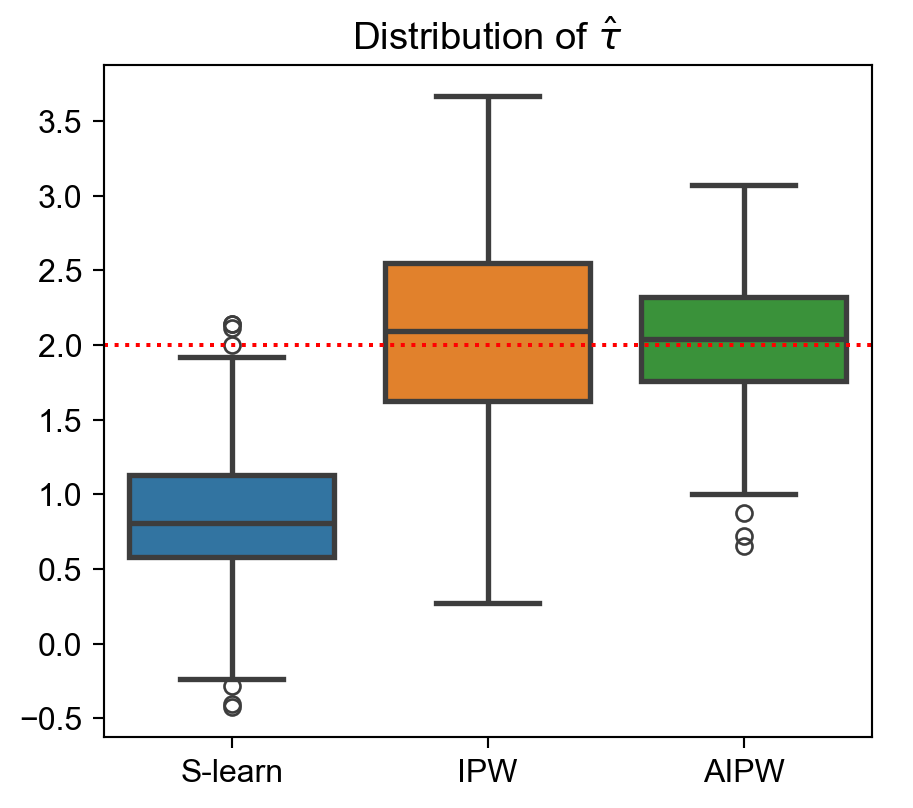
Wrong propensity score model:
ax = pw.Brick(figsize=(4, 3.5))
wrong_ps_df = simulate_estimators(
['age'], ['male', 'hours'], D="dark_mode", y="read_time"
)
wrong_ps_plot = sns.boxplot(
data=pd.melt(wrong_ps_df), x='variable', y='value', hue='variable',
ax=ax,
linewidth=2
);
ax.set_title("Distribution of $\hat τ$");
ax.axhline(2, c='r', ls=':');
ax.savefig()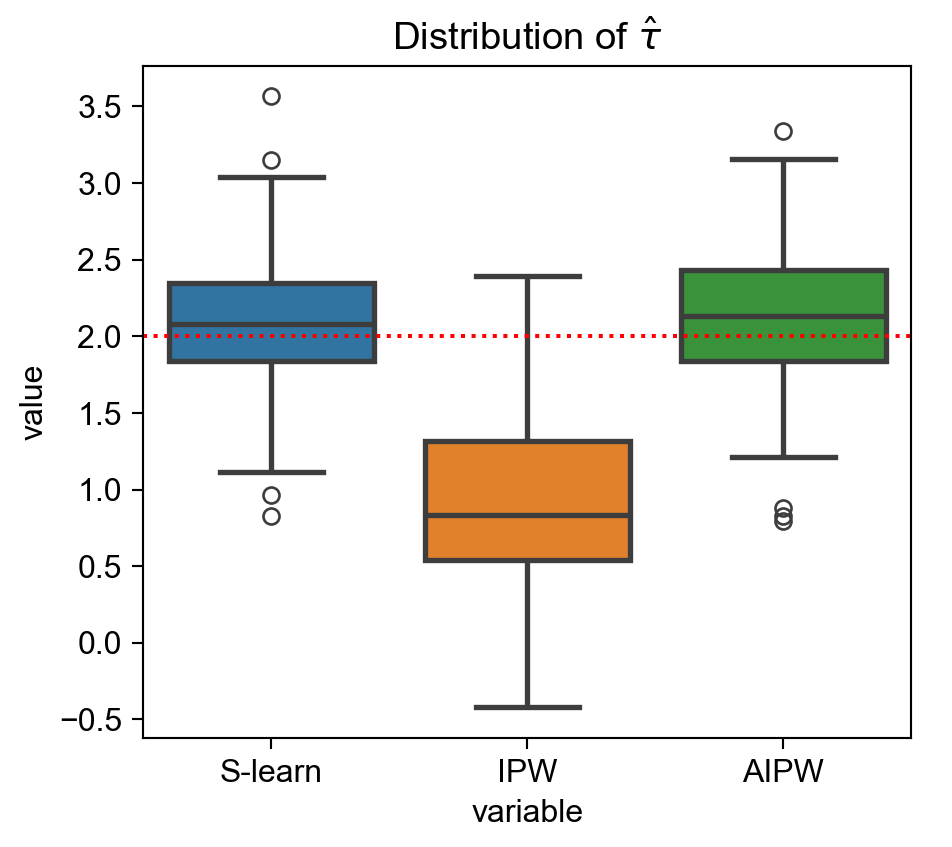
DSAN 5650 Week 9: Instrumental Variables