Week 5: Hash Tables and Binary Search Trees

DSAN 5500: Data Structures, Objects, and Algorithms in Python

Jeff Jacobs

jj1088@georgetown.edu

Thursday, February 6, 2025

Schedule

Today’s Planned Schedule:

	Start	End	Topic
Lecture	6:30pm	7:30pm	HashTable: Linear to Constant Efficiency 🤯 →
	7:30pm	8:00pm	BinarySearchTree: The Final Missing Piece! →
Break!	8:00pm	8:10pm
	8:10pm	9:00pm	BinarySearchTree: The Final Missing Piece! →

Hash Tables

• (Spoiler alert, so you know I’m not lying to you: this is a LinkedList with some additional structure!)
• You just got hired as a cashier (Safeway cashiering alum myself 🫡)
• The scanner is broken (spoiler #2: the scanner uses a hash table), so you start writing down items along with their prices, one-by-one, as items come in…

Our List of (Item, Price) Pairs

price_list = []
price_list.append(('Banana', 10))
price_list.append(('Apple', 2))
price_list.append(('Four Loko', 5))
price_list

[('Banana', 10), ('Apple', 2), ('Four Loko', 5)]

• As the list gets longer, it gets harder and harder to find where you wrote down a specific item and its price
• As you now know, you could use linear search, \(\overline{O}(n)\), or if you ensure alphabetical order (an invariant!), you could use binary, divide-and-conquer search, \(\overline{O}(\log_2(n))\)
• We can do even better: \(\overline{O}(1)\). First w/magic, but then math

Strange-At-First Technique for Algorithm Analysis: Oracles

• What if we had a magical wizard who could just tell us where to find an item we were looking for?
• Sounds like I’m joking or saying “what if we had a billion $ and infinite aura and we could fly and walk through walls”
• And yet, through the magic of math and computer science, there are concrete hashing algorithms which ensure (in a mathematically-provable way!) “almost certain” \(\overline{O}(1)\) lookup time

Mathematical Strategy of Oracles

• We’ll use a concrete, simplified hash function to illustrate
• Mathematically we’ll be able to get something like

\[ T(n) = \overline{O}(1 + \underbrace{\epsilon}_{\mathclap{\text{Collision rate}}} \cdot n) \]

• Which tells us: if we had an oracle who could ensure near-0 collision rates, then \(T(n) = \overline{O}(1)\).
• And, by a beautiful division-of-labor, other computer scientists figure out the near-0 collision rates part, giving us

\[ p^{✅} = [T(n) = \overline{O}(1 + \epsilon n)], q^{✅} = [\epsilon \approx 0],\text{ so } p \wedge q \implies T(n) \overset{✅}{=} \overline{O}(1). \]

Back to the Price List

• Our hash function: hash(item) = first letter of item

\[ h(\texttt{x}) = \texttt{x[0]} \]

• h('Banana') = 'B', h('Monkey') = 'M'
• With this function in hand, we can create a length-26 array, one slot for each letter in alphabet, and then write down (item, price) pairs in whatever slot item hashes to

The Importance of Differentiating Operations: Insertion vs. Lookup

• So far, we have \(\overline{O}(1)\) insertion via hashing
• We also get \(\overline{O}(1)\) lookup!
• When customer hands us an item (say, 'Banana'), we compute the hash (B), look in that slot, and obtain the price for bananas.
• We also get \(\overline{O}(1)\) updating (hash to find the old price, update it to have new price) and \(\overline{O}(1)\) deletion (hash to find the slot containing the item, then erase it from that slot)

So What’s the Catch???

• BLUEBERRIES show up to ruin our day (as usual 😞)
• We hash, so far so good: h('Blueberries') = 'B'
• But then we go to the B slot and see that (Bananas, 10) is already there!!! Wtf do we do here… don’t panic!
• The answer? We open our HW2 from DSAN 5500 and remember that we have our lovely friend the LinkedList that we can use whenever and however we want!

Arrays vs. Linked Lists

• Jeff is hiding something here… Why jump to LinkedList? Why not just… another length-26 array, for example?
• For this we open up our Week 1 slides and remember the stack vs. heap distinction: we know how many letters in the alphabet, we don’t know how many items starting with B (or, if we do, we want to be able to expand/contract our price list to handle new/discontinued items)
• Terminology for this kind of “hybrid” data structure: HashTable is an Array that “degenerates into” a LinkedList (when there are collisions)

Look How Far We Came!

• Last week: Only structure we knew allowing insertion (LinkedList) was \(\overline{O}(n)\) for everythihg
• This week: New structure where suddenly everything is \(\overline{O}(1)\), except in “unlucky” cases, in which it partially “degenerates” into a LinkedList
• \(\implies\) The “inevitable” \(\overline{O}(n)\) runtime has transformed into the unlucky worst-case upper bound (feels like yesterday, all this was a dream)
• \(\implies\) By taking core data structures/algorithms from your toolkit, you can “piece together” hybrid structures whose whole (runtime) is better than the sum of its parts

Hash Tables: tl;dr Edition

• Keys \(k \in \mathcal{K}\) are plugged into a (deterministic) hash function \(h: \mathcal{K} \rightarrow \{1, \ldots, N\}\), producing an index where \(k\) is stored
• If nothing at that index yet, store \((k,v)\) in empty slot
• If already an item at that index, we have a ⚠️collision⚠️
• We could just throw away the old value (HW2 Part 1)
• Otherwise, need a way to store multiple items in one slot… (a way to dynamically grow storage at given index)
• Solution you know so far: Linked Lists
• New solution: Binary Search Trees!

Binary Search Trees

• If you’ve been annoyed by how long we’ve talked about Linked Lists for… this is where it finally pays off!

BST: The Final Missing Piece

• Just a glorified LinkedList! We’ll be able to take our HashMap and “drop in” the BST to play the role LinkedList is playing right now
• If collision, we’ll create a BST with its \(\overline{O}(\log(n))\) operations, rather than a LinkedList with its \(\overline{O}(n)\) operations
• \(\implies\) HashMap will go from:
  • \(\overline{O}(1)\) best-case but \(\overline{O}(n)\) worst-case to
  • \(\overline{O}(1)\) best-case but \(\overline{O}(\log_2(n))\) worst-case!

Linked Lists + Divide-and-Conquer = BSTs

• By now, the word “Linked List” should make you groan, cross your arms and start tapping your feet with impatience
• “Here we go again… the Linked List is gonna make us traverse through every single element before we reach the one we’re looking for” 😖
• Linked List = Canon in D
• Binary Search Tree = Canon in D played by Hiromi Uehara…

Hiromi Uehara

The Metaphor Goes Deep!

• Uehara’s Canon in D = Pachelbel’s + Fancier notes/rhythms on top of it
• Binary Search Trees = Linked Lists + Fancier structure built on top of it
  • Specifically: “next” pointer can now branch left or right, to ensure ordering of nodes

class LinkedListNode:
    @property content
    @property next

class BinarySearchTreeNode:
    @property content
    @property left
    @property right

Visualizing BSTs

from hw2 import LinkedList, InventoryItem, BinarySearchTree
bst = BinarySearchTree()
item1 = InventoryItem('Mango', 50)
bst.add(item1)
item2 = InventoryItem('Pickle', 60)
bst.add(item2)
item3 = InventoryItem('Artichoke', 55)
bst.add(item3)
item5 = InventoryItem('Banana', 123)
bst.add(item5)
item6 = InventoryItem('Aardvark', 11)
bst.add(item6)
HTML(visualize(bst))

Practical Considerations

• Hash Maps: Only useful if keys are hashable
  • Python has a built-in collections.abc.Hashable class, such that hash(my_obj) works iff isinstance(my_obj, Hashable)
• Binary Search Trees: Only useful if keys have an ordering
  • “Standard” classes (int, str, datetime) come with implementations of ordering, but if you make your own class you need to implement the ordering for it!
• (Linked Lists still work for non-hashable/orderable objects!)

Why ==, <, >= “Just Work”

• Not magic! Someone has explicitly written a set of functions telling Python what to do when it sees e.g. obj1 < obj2
• Example: let’s implement an ordering of vectors \(\mathbf{x} \in \mathbb{R}^2\) based on Pareto dominance

Ordering Vectors via Pareto Dominance

class UtilVector:
    def __init__(self, u1, u2):
        self.u1 = u1
        self.u2 = u2
    
    def __eq__(self, other):
        if not isinstance(other, UtilVector):
            return NotImplemented
        return self.u1 == other.u1 and self.u2 == other.u2

    def __ne__(self, other):
        if not isinstance(other, UtilVector):
            return NotImplemented
        return self.u1 != other.u1 or self.u2 != other.u2
    
    def __gt__(self, other):
        if not isinstance(other, UtilVector):
            return NotImplemented
        return self.u1 > other.u1 and self.u2 >= other.u2 or self.u1 >= other.u1 and self.u2 > other.u2

    def __ge__(self, other):
        return self.__gt__(other) or self.__eq__(other)
        
    def __lt__(self, other):
        if not isinstance(other, UtilVector):
            return NotImplemented
        return other.__gt__(self)

    def __le__(self, other):
        return self.__lt__(other) or self.__eq__(other)
xA = UtilVector(2, 2)
xB = UtilVector(3, 2)
print(xB > xA)
xC = UtilVector(2, 3)
print(xC > xB)
import itertools
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
x0 = UtilVector(4, 6)
util_vals = np.arange(0, 11, 0.5)
util_pairs = list(itertools.product(util_vals, util_vals))
util_df = pd.DataFrame(util_pairs, columns=['x','y'])
def compare_to_x0(row):
    row_vec = UtilVector(row['x'], row['y'])
    gt_result = int(row_vec > x0)
    lt_result = int(row_vec < x0)
    return gt_result - lt_result
util_df['greater'] = util_df.apply(compare_to_x0, axis=1)
#my_palette = sns.color_palette(['#E69F00','lightgray','#CCFFCC'])
my_palette = sns.color_palette(['#FF3535','lightgray','#35FF35'])
sns.relplot(
    data=util_df,
    x='x', y='y',
    hue='greater',
    palette=my_palette,
    marker='X', s=150
);
x0_df = pd.DataFrame({'x': [4], 'y': [6]})
plt.scatter(data=x0_df, x='x', y='y', color='black')
plt.gca().set_aspect('equal')

True
False

Back to BSTs

• For HW2, we provide you with an InventoryItem class
• Two instance variables: item_name and price
• Equivalence relations:
  • __eq__(other), __ne__(other)
• Ordering relations:
  • __lt__(other), __le__(other), __gt__(other), __ge__(other)
• Bonus: __repr__() and __str__()

Node Traversal: Computational Tree-Climbing

LLs \(\rightarrow\) BSTs: The Hard Part

• When we were working with LinkedLists, we could access all items by just “looping through”, from one element to the next, printing as we go along.
• But… for a BinarySearchTree, since our structure can now branch as we traverse it… How do we “loop through” a BST?
• Two fundamentally different ways to traverse every node in our BST
• “Opposites” of each other, so that one is often extremely efficient and the other extremely inefficient for a given task
• Your job as a data scientist is to think carefully about which one is more efficient for a given goal!

Two Ways to Traverse: IRL Version

• Imagine we’re trying to learn about a topic \(\tau\) using Wikipedia, so we find its article \(\tau_0\)
• There are two “extremes” in terms of strategies we could follow for learning, given the contents of the article as well as the links it contains to other articles

Depth-First Search (DFS)

• Open \(\tau_0\) and start reading it; When we encounter a link we always click it and immediately start reading the new article.
• If we hit an article with no links (or a dead end/broken link), we finish reading it and click the back button, picking up where we left off in the previous article. When we reach the end of \(\tau_0\), we’re done!

Breadth-First Search (BFS)

• Bookmark \(\tau_0\) in a folder called “Level 0 Articles”; open and start reading it
• When we encounter a link, we put it in a “Level 1 Articles” folder, but continue reading \(\tau_0\) until we reach the end.
• We then open all “Level 1 Articles” in new tabs, placing links we encounter in these articles into a “Level 2 Articles” folder, that we only start reading once all “Level 1 Articles” are read
• We continue like this, reading “Level 3 Articles” once we’re done with “Level 2 Articles”, “Level 4 Articles” once we’re done with “Level 3 Articles”, and so on. (Can you see a sense in which this is the “opposite” of DFS?)

• …Let’s try them out! I clicked “Random Article” and got Eustache de Saint Pierre

Two Ways to Traverse: Picture Version

from hw2 import IterAlgorithm, NodeProcessor
visualize(bst)

print("DFS:")
dfs_processor = NodeProcessor(IterAlgorithm.DEPTH_FIRST)
#print(type(dfs_processor.node_container))
dfs_processor.iterate_over(bst)

print("\nBFS:")
bfs_processor = NodeProcessor(IterAlgorithm.BREADTH_FIRST)
#print(type(bfs_processor.node_container))
bfs_processor.iterate_over(bst)

DFS:
InventoryItem[item_name=Mango,price=50]
InventoryItem[item_name=Pickle,price=60]
InventoryItem[item_name=Artichoke,price=55]
InventoryItem[item_name=Banana,price=123]
InventoryItem[item_name=Aardvark,price=11]

BFS:
InventoryItem[item_name=Mango,price=50]
InventoryItem[item_name=Artichoke,price=55]
InventoryItem[item_name=Pickle,price=60]
InventoryItem[item_name=Aardvark,price=11]
InventoryItem[item_name=Banana,price=123]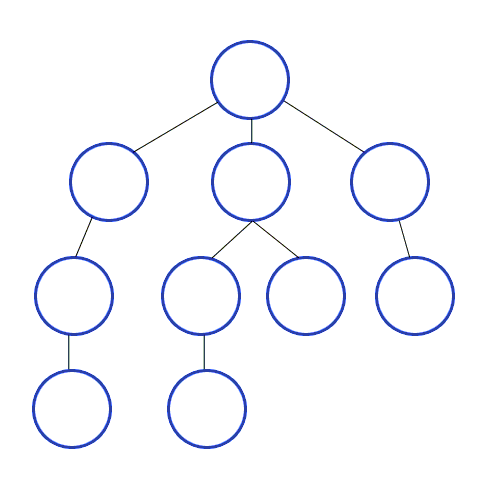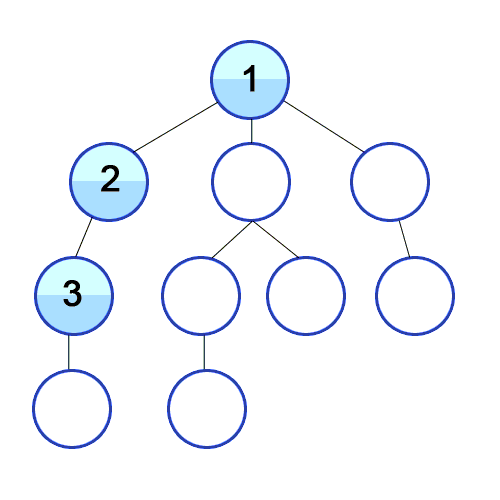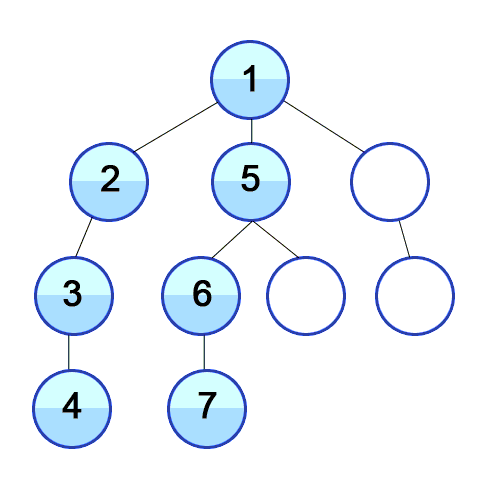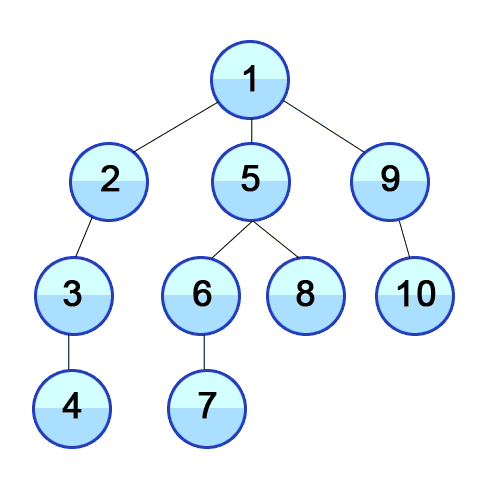

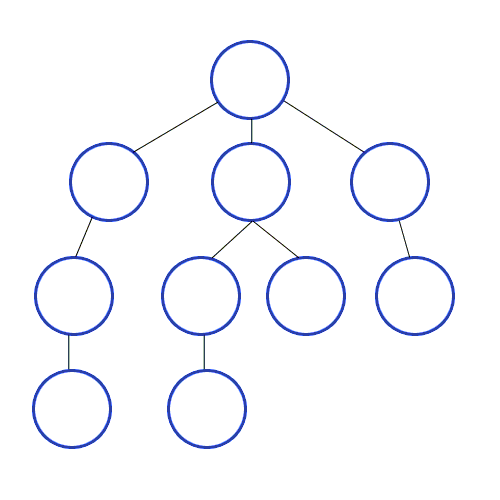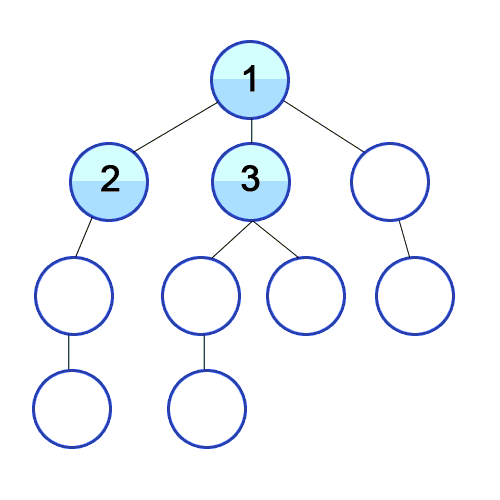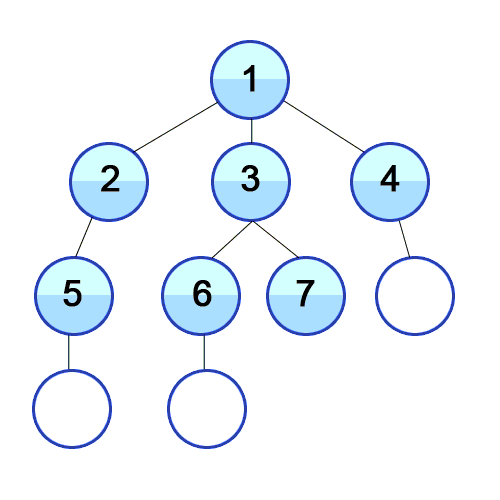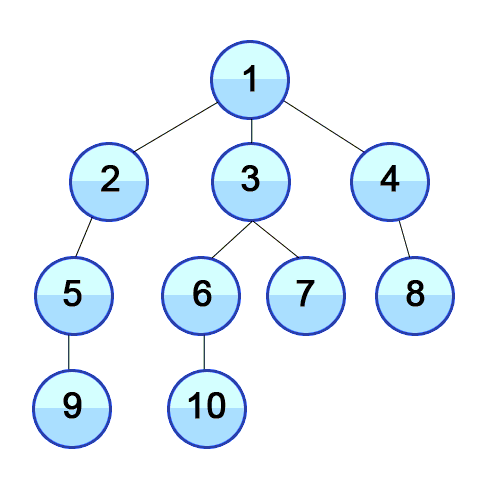
Two Ways to Traverse: In-Words Version

1. Depth-First Search (DFS): With this approach, we iterate through the BST by always taking the left child as the “next” child until we hit a leaf node (which means, we cannot follow this left-child pointer any longer, since a leaf node does not have a left child or a right child!), and only at that point do we back up and take the right children we skipped.
2. Breadth-First Search (BFS): This is the “opposite” of DFS in the sense that we traverse the tree level-by-level, never moving to the next level of the tree until we’re sure that we have visited every node on the current level.

Two Ways to Traverse: Animated Version

Depth-First Search (from Wikimedia Commons)

Breadth-First Search (from Wikimedia Commons)

Two Ways to Traverse: Underlying Data Structures Version

• Now that you have some intuition, you may be thinking that they might require very different code to implement 🤔
• This is where the mathematical-formal linkage between the two becomes ultra helpful!
• It turns out (and a full-on algorithmic theory course makes you prove) that

1. Depth-First Search can be accomplished by processing nodes in an order determined by adding each to a stack, while
2. Breadth-First Search can be accomplished by processing nodes in an order determined by adding each to a queue!

• \(\implies\) Literally identical code, “pulling out” the word stack and replacing it with the word queue within your code (or vice-versa).
• If you have your Software Engineer Hats on, you’ll recognize this as a job for an abstraction layer!

Two Ways to Traverse: HW2 Version

• You’ll make a class called NodeProcessor, with a single iterate_over(tree) function
• This function—without any changes in the code or even any if statements!—will be capable of both DFS and BFS
• It will take in a ThingContainer (could be a stack or a queue, you won’t know which), which has two functions:
  • put_new_thing_in(new_thing)
  • take_existing_thing_out()

Three Animals in the DFS Species

DFS Procedure	Algorithm
Pre-Order Traversal	1. Print node 2. Traverse left subtree 3. Traverse right subtree
In-Order Traversal 🧐‼️	1. Traverse left subtree 2. Print node 3. Traverse right subtree
Post-Order Traversal	1. Traverse left subtree 2. Traverse right subtree 3. Print node

The Three Animals Traverse our Inventory Tree

visualize(bst)

Final Notes for HW2

• The last part challenges you to ask: why stop at a hash based on just the first letter of the key?
• We could just as easily use the first two letters:
• h('AA') = 0, h('AB') = 1, …, h('AZ') = 25,
• h('BA') = 26, h('BB') = 27, …, h('BZ') = 51,
• h('CA') = 52, …, h('ZZ') = 675.
• You will see how this gets us even closer to the elusive \(O(1)\)! And we could get even closer with three letters, four letters, … 🤔🤔🤔