Week 11: Fear and Loathing on the Pareto Frontier

DSAN 5450: Data Ethics and Policy
Spring 2025, Georgetown University

Jeff Jacobs

jj1088@georgetown.edu

Wednesday, April 2, 2025

Where We Left Off…

\[ \DeclareMathOperator*{\argmax}{argmax} \DeclareMathOperator*{\argmin}{argmin} \newcommand{\bigexp}[1]{\exp\mkern-4mu\left[ #1 \right]} \newcommand{\bigexpect}[1]{\mathbb{E}\mkern-4mu \left[ #1 \right]} \newcommand{\definedas}{\overset{\small\text{def}}{=}} \newcommand{\definedalign}{\overset{\phantom{\text{defn}}}{=}} \newcommand{\eqeventual}{\overset{\text{eventually}}{=}} \newcommand{\Err}{\text{Err}} \newcommand{\expect}[1]{\mathbb{E}[#1]} \newcommand{\expectsq}[1]{\mathbb{E}^2[#1]} \newcommand{\fw}[1]{\texttt{#1}} \newcommand{\given}{\mid} \newcommand{\green}[1]{\color{green}{#1}} \newcommand{\heads}{\outcome{heads}} \newcommand{\iid}{\overset{\text{\small{iid}}}{\sim}} \newcommand{\lik}{\mathcal{L}} \newcommand{\loglik}{\ell} \DeclareMathOperator*{\maximize}{maximize} \DeclareMathOperator*{\minimize}{minimize} \newcommand{\mle}{\textsf{ML}} \newcommand{\nimplies}{\;\not\!\!\!\!\implies} \newcommand{\orange}[1]{\color{orange}{#1}} \newcommand{\outcome}[1]{\textsf{#1}} \newcommand{\param}[1]{{\color{purple} #1}} \newcommand{\pgsamplespace}{\{\green{1},\green{2},\green{3},\purp{4},\purp{5},\purp{6}\}} \newcommand{\prob}[1]{P\left( #1 \right)} \newcommand{\purp}[1]{\color{purple}{#1}} \newcommand{\sign}{\text{Sign}} \newcommand{\spacecap}{\; \cap \;} \newcommand{\spacewedge}{\; \wedge \;} \newcommand{\tails}{\outcome{tails}} \newcommand{\Var}[1]{\text{Var}[#1]} \newcommand{\bigVar}[1]{\text{Var}\mkern-4mu \left[ #1 \right]} \]

Operationalizing Power

• Equally good outside options \(\implies\) can contract to Pareto-optimal point \(o^P\)
• \(i\) has better outside options \(\implies\) can make take it or leave it offer to \(j\):
  • “You (\(j\)) fish 6 hrs all the time. I (\(i\)) fish 6 hrs 41% of time, 8 hrs otherwise”

• Ever so slightly better for \(j\) \(\implies\) \(j\) accepts (Behavioral econ: \(j\) accepts if 41% meets subjective fairness threshold; observed across many many cultures!)
• Later / next week: observe policy with outcome \(o^{C}_{i \rightarrow j} \iff\) policy values \(i\)’s welfare more than \(j\)’s welfare (inferred social welfare weights \(\omega_i > \omega_j\))

Since We’ve Already Opened the Pandora’s Box of Utility…

From Ryan Safner’s History of Economic Thought: Welfare Economics

• Bluey obtains greater utility within the same budget by moving from \(E^1\) to \(O^1\)

Two Can Play This Game…

• Bluey obtains greater utility within the same budget by moving from \(E^1\) to \(O^1\)
• Greenie obtains greater utility within the same budget by moving from \(E^2\) to \(O^2\)

The Edgeworth Box

Rotate Greenie’s box 180° and superimpose onto Bluey’s

The Contract(!) Curve

• From initial endowment \(E\), if allowed to trade, “rational” players can reach any allocation along dashed contract curve from \(G\) to \(B\)… (Why not \(A\) or \(H\)?)
• So, what determines which of these points they end up at? (Middle name hint)

First Fundamental Theorem of Welfare Economics

Theorem: [Antecedents (Coase Conditions)] \(\Rightarrow\) markets produce Pareto-optimal outcomes

• Even commie Jeff finds proof+corollaries compelling / convincing / empirically-supported
• (It’s a full-on proof, in the mathematical sense, so doesn’t rly matter what I think; I just mean, imo, important and helpful to think through for class on policy!)
• Ex: Conditional on antecedents [(Coase) minus (perfect competition) plus (thing must be allocated via markets)], \(\uparrow\) Competition \(\leadsto\) More efficient allocations

Payoff from Jeff Pointing at Things Saying “Antecedents!” 500x

Consequent only true if antecedents hold! Otherwise, proper answer becomes “It depends! Let’s see if data can help us find out!” (Will minimum wage hurt/help blah blah blah… “It depends! Tell me the details!”) (Will new condos blah blah blah yimby nimby…) (Will re-allocating welfare budget from \(X\) to \(Y\) blah blah blah… 👀 HW4)

[Economic inequality] is a social law, something in the nature of man. (Pareto 1896)

We’ve got a [thing] made by men, isn’t that something we should be able to change? (Steinbeck 1939)

Coase Antecedents \(\approx\) equalized power!

• Ex 1: Perfect Competition \(\Rightarrow\) (\(\neg\) monopoly) \(\wedge\) (\(\neg\) monopsony) \(\Rightarrow\) everyone’s outside option equally good \(\Rightarrow\) no take-it-or-leave-it coercion possible (try to coerce, I’ll say no and go to one of the other \(\infty\) people offering equally good options)
• Ex 2: No Informational Asymmetries \(\Rightarrow\) Can’t “trick me” into buying defective product (Akerlof (1970), “Market for Lemons”)

So… What Happens When Antecedents Don’t Hold?

• \(\neg\)(Coase Antecedents) \(\Rightarrow\) Unequal Power… Puts us in the realm of Descriptive Ethics! (Thucydides!)
• Like how Gauss-Markov Assumptions \(\Rightarrow\) OLS is BLUE, yet our whole field (at least, a whole class, DSAN5300) built on what to do when G-M Assumptions don’t hold
• For policy development, helpful to think through
  • which cases “break” FFT (more honored in the breach)
  • How each violation might be “fixed” through policy¹
• Our violation: No externalities assumption
  • Possible policy “fixes”: property rights, market-socialist nationalization

1. Recall W01: Earned Income Tax Credits, Emissions Markets, Climate Engineering, Antitrust Legistlation \(\in \text{Policy Set}\); Black Panther Community Police Patrols, Blowing Up Oil Pipelines (Malm 2021), Bolshevik Revolution also \(\in \text{Policy Set}\)

Part 2 Suddenly Collides with Part 1: Property Rights

• Rawlsian Rights: Vetos on societal decisions; Constitution can make some inalienable (can’t sell self into slavery), some alienable
• Property rights: alienable. You can gift or sell the rights if you want (veto is over society just, like, taking your property if someone else would be happier with it)

Case : Society decides Right to Clean Air \(\prec\) Right to Smoke \(\Rightarrow\) Start at \(E\)

• \(A\) can pay \(B\) to alienate right (Pay $50/month, can smoke 5 ciggies) \(\leadsto\) \(X\)
• Movement along light blue curve: giving up \(x\) money for \(y\) smoke, equally happy. \(u_A(p)\) identical for \(p\) on curve
• Movement to higher light blue curve () \(\Rightarrow\) greater utility \(u_A' > u_A\)

Case Society decides Smoke \(\prec\) Clean Air \(\Rightarrow\) Repeat for \(E' \leadsto X'\)

“Edgeworth Box” for Right to Smoke vs. Right to Clean Air: \(A\), \(B\) are roommates; \(A\) loves smokin, \(B\) loves clean air

Why Exactly Does [Commodifying Rights] Sometimes Enable [“Cancelling Out” Externalities]?

• The key: Forces agent \(i\) to pay a cost for inflicting disutility on agent \(j\)!
• (Here plz note: “\(X\) sometimes enables \(Y\)” does not mean \(X\) is a necessary or sufficient condition for \(Y\)! Think of walking into a dark room, trying different light switches until one turns on the overhead light)
• Dear reader, I know what you’re thinking… But Jeff!! This is all so abstract and theoretical!! We’re sick of your ivory-tower musings, get your head out of the clouds and make it relevant to our day-to-day lives, by relating it back to Yugoslavia’s 1965 economic reforms!!
• Don’t worry, I’ve listened to your concerns, and the next slide is here for you 😌

Externalities: I Get Reward, Others Pay Cost 🥳

• Firm \(S\) produces amount of steel \(s\), pollution \(x\)
• Firm \(F\) “produces” amount of fish \(f\)
• \(S\) optimizes

\[ s^*_{\text{Priv}}, x^*_{\text{Priv}} = \argmax_{s,x}\left[ p_s s - c_s(s, x) \right] \]

• While \(F\) optimizes

\[ f^*_{\text{Priv}} = \argmax_{f}\left[ p_f f - c_f(f, x) \right] \]

• If [Yugoslavia-style] nationalized, new optimization of joint steel-fish venture is

\[ s^*_{\text{Yugo}}, f^*_{\text{Yugo}}, x^*_{\text{Yugo}} = \argmax_{s, f, x}\left[ p_s s + p_f f - c_s(s, x) - c_f(f, x) \right] \]

• Can prove/“prove” that \(o(s^*_{\text{Yugo}}, f^*_{\text{Yugo}}, x^*_{\text{Yugo}})\) Pareto-dominates \(o(s^*_{\text{Priv}}, x^*_{\text{Priv}}, f^*_{\text{Priv}})\)
• So… what determines which agents get to ignore externalities? (Dead horse)

Social Welfare Functionals

Functionals?

• You probably know what a function \(f(x)\) is; a functional is a function of functions: \(\mathscr{G}(f)\)
• It’s from math, which is scary, but it’s just notation to remind us that we’re analyzing functions of functions
• In our case, they “work the same way” as regular functions, e.g., \(\mathscr{G}(f,g) = f^2 + g^2\), so \(f(x) = x, g(x) = 2x \Rightarrow \mathscr{G}(f,g)(x) = x^2 + 4x^2 = 5x^2\)

We Live In A Society, Part 2

• Utilitarianism, Kant, Rawls can all be modeled as Social Welfare Functionals

\[ W(\mathbf{u}) = W(u_1, \ldots, u_n) \Rightarrow W(\mathbf{u})(x) = W(u_1(x), \ldots, u_n(x)) \]

• \(u_i(x)\): Given bundle of resources \(x\), how much utility does \(i\) experience? \(u_i: \mathcal{X} \rightarrow \mathbb{R}\)
• \(W(\mathbf{u})\): Aggregates \(u_i(x)\) over all \(i\), to produce measure of overall welfare of society. For \(N\) people, \(W: (\mathcal{X} \rightarrow \mathbb{R})^N \rightarrow \mathbb{R}\).
• Standard assumption: \(W\) additive \(\Rightarrow W(\mathbf{u}) = \sum_{i=1}^n \omega_iu_i(x)\)
  • \(\omega_i \equiv \frac{\partial W}{\partial u_i}\) is \(i\)’s welfare weight (❗️)
• Welfare-Economic definition of Utilitarianism: Literally just \(\omega_i = 1 \; \forall i\)
• (HW4) Decomposition to evaluate bias in policy impacts: from observed allocation \(x_i\) and marginal utility \(u'_i(x)\), can…
  • Infer \(\widehat{\omega}_i\) (how much policy does value person \(i\)), then
  • Compare with \(\omega_i^*\) (how much policy should value person \(i\)… conjoint survey) 🤯

Alternative SWF Specifications

• Social values

\[ W(\underbrace{v_1, \ldots, v_n}_{\text{Values}})(x) \overset{\text{e.g.}}{=} \omega_1\underbrace{v_1(x)}_{\text{Privacy}} + \omega_2\underbrace{v_2(x)}_{\mathclap{\text{Public Health}}} \]

• Stakeholder Analysis

\[ W(\underbrace{s_1, \ldots, s_n}_{\text{Stakeholders}})(x) = \omega_1\underbrace{u_{s_1}(x)}_{\text{Teachers}} + \omega_2\underbrace{u_{s_2}(x)}_{\text{Parents}} + \omega_3\underbrace{u_{s_3}(x)}_{\text{Students}} + \omega_4\underbrace{u_{s_4}(x)}_{\mathclap{\text{Community}}} \]

• (Adapted from this great intro video!)

The Conveniently-Left-Out Detail

• Recall, e.g., predictive parity:

\[ \mathbb{E}[Y \mid D = 1, A = 1] = \mathbb{E}[Y \mid D = 1, A = 0] \]

• Who decides which \(Y\) to pick? (Kasy and Abebe 2021)
• Answer: Whoever picks the objective function!
• Profit-maximizing firm: \(\max\left\{ \mathbb{E}[D (Y - c)]\right\} \Rightarrow\) (Discrimination if and only if bad at profit-maximizing)
• Welfare-maximizing policymaker: \(\max\{ W(u_1(D), \ldots, u_n(D)) \}\)
• Do these align? Sometimes yes, sometimes no (See: Welfare Theorems and their antecedents, and/or Becker (1957))

Remaining (Challenging) Details

• Who gets included in the SWF?
• People in one household? One community? One state? One country?
• People in the future?
• Animals?
• …OUR BEAUTIFUL ENVIRONMENT??? (Figure 1)

Figure 1: Our beautiful environment

Back to Utilitarian SWF

• Easy mode (possibly/probably your intuition?): Everyone’s welfare weight should be equal, \(\omega_i = \frac{1}{n}\)

\[ W(u_1, \ldots, u_n)(x) = \frac{1}{n}u_1(x) + \cdots + \frac{1}{n}u_n(x) \]

• \(\implies\) Utilitarian Social Welfare Functional!
• The Silly Problem of Utilitarian SWF: What if everyone is made happy by \(u_{\text{Jeef}} = -999999999\)?

The Hard Problem of Utilitarian SWF

While the rhetoric of “all men [sic] are born equal” is typically taken to be part and parcel of egalitarianism, the effect of ignoring the interpersonal variations can, in fact, be deeply inegalitarian, in hiding the fact that equal consideration for all may demand very unequal treatment in favour of the disadvantaged (Sen 1992)

• \(\implies\) “Equality of What?”
• What is the “thing” that egalitarianism obligates us to equalize (the equilisandum/equilisanda): Utility? Opportunity? Resources? Money? Freedom from [\(X\)]? Freedom to [\(Y\)]?

Utility \(\rightarrow\) Social Welfare

Externalities

• Jeef and Keef are roommates: Jeef loves listening to Tony Danza Tapdance Extravaganza, but Keef is normal and slowly dies inside with each additional song

Songs	Jeef	Keef	Total
0	0	0	0
1	13	-2	11
2	18	-6	12
3	24	-13	11
4	28	-20	8
5	30	-42	-12

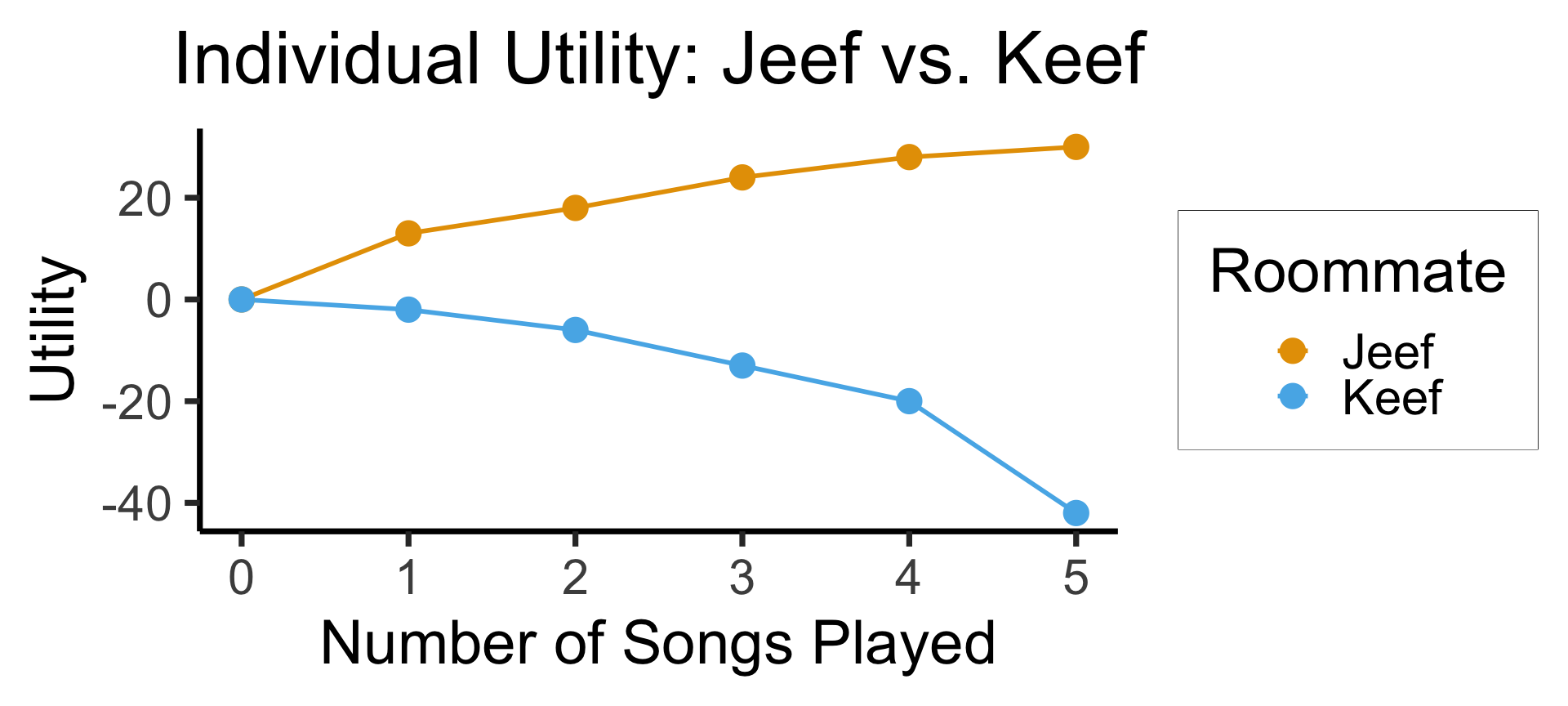
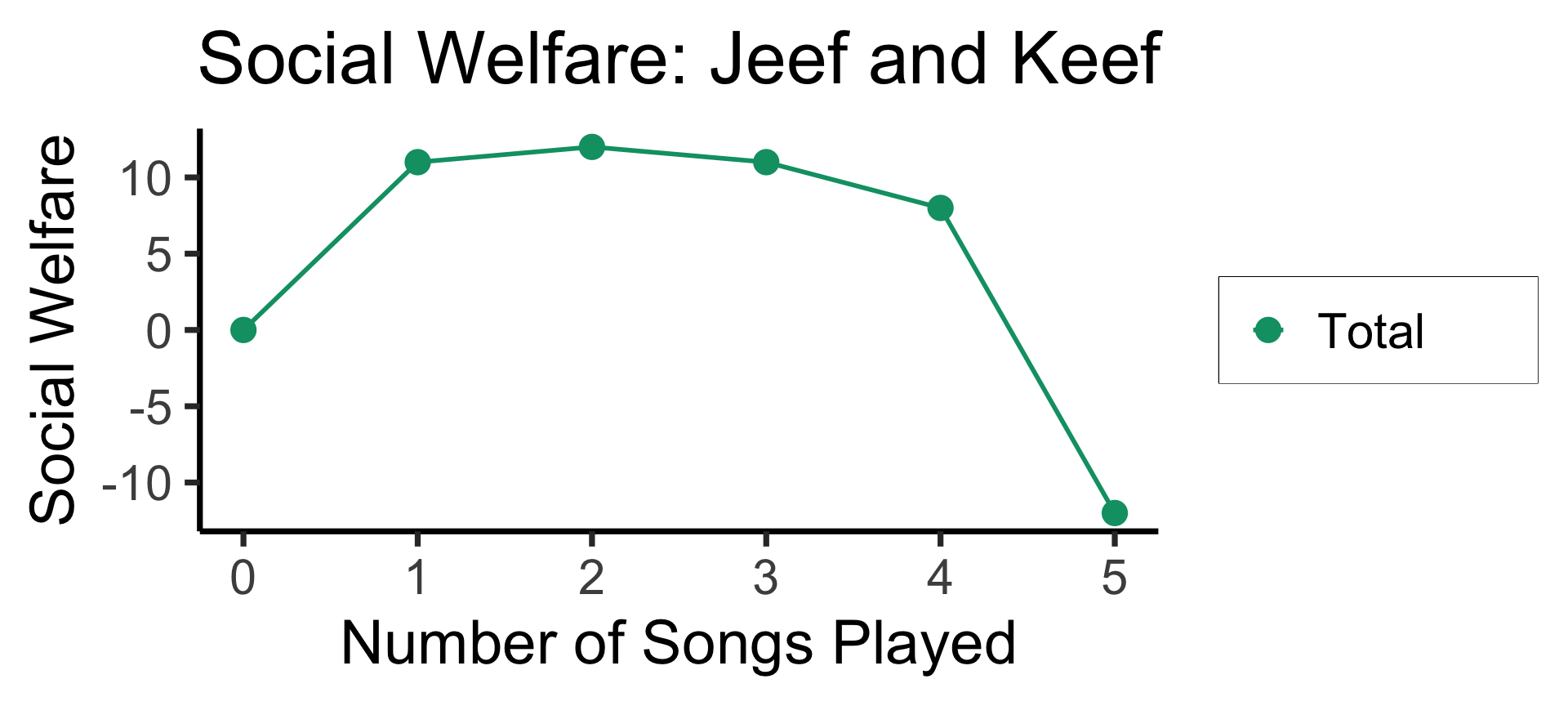
So What’s the Issue?

• These utility values are not observed
• If we try to elicit them, both Jeef and Keef have strategic incentives to lie (over-exaggerate)
• Jeef maximizes own utility by reporting \(u_j(s) = \infty\)
• Keef maximizes own utility by reporting \(u_k(s) = -\infty\)
• (…Second price auctions tho)

Now with Scarce Resources

• In a given week, Jeef and Keef have 14 meals and 7 aux hours to divide amongst them

\[ \begin{align*} \max_{m_1,m_2,a_1,a_2}& W(u_1(m_1,a_1),u_2(m_2,a_2)) \\ \text{s.t. }& m_1 + m_2 \leq 14 \\ \phantom{\text{s.t. }} & ~ \, a_1 + a_2 \; \leq 7 \end{align*} \]

• Let’s assume \(u_i(m_i, a_i) = m_i + a_i\) for both
• \(\Rightarrow\) One solution: \(m_1 = 14, m_2 = 0, a_1 = 7, a_2 = 0\)…
• \(\Rightarrow\) Another: \(m_1 = 0, m_2 = 14, a_1 = 0, a_2 = 7\)…
• Who decides? Any decision implies \(\omega_1, \omega_2\) (\(\omega_1 + \omega_2 = 1\))

Let’s Talk Projects!

References

Akerlof, George A. 1970. “The Market for "Lemons": Quality Uncertainty and the Market Mechanism.” The Quarterly Journal of Economics 84 (3): 488–500. https://doi.org/10.2307/1879431.

Becker, Gary S. 1957. The Economics of Discrimination. University of Chicago Press.

Kasy, Maximilian, and Rediet Abebe. 2021. “Fairness, Equality, and Power in Algorithmic Decision-Making.” In Proceedings of the 2021 ACM Conference on Fairness, Accountability, and Transparency, 576–86. FAccT ’21. New York, NY, USA: Association for Computing Machinery. https://doi.org/10.1145/3442188.3445919.

Malm, Andreas. 2021. How to Blow Up a Pipeline. Verso Books.

Pareto, Vilfredo. 1896. Cours d’Économie politique. Librairie Droz.

Sen, Amartya. 1992. Inequality Reexamined. Clarendon Press.

Steinbeck, John. 1939. The Grapes of Wrath. Penguin.