Regression vs. PCA

DSAN 5300: Statistical Learning

Author

Affiliation

Jeff Jacobs

jj1088@georgetown.edu

The Central Tool of Data Science

source("../../dsan-globals/_globals.r")

$$$$

• If science is understanding relationships between variables, regression is the most basic but fundamental tool we have to start measuring these relationships
• Often exactly what humans do when we see data!

library(ggplot2)
library(tibble)
x_data <- seq(from=0, to=1, by=0.02)
num_x <- length(x_data)
y_data <- x_data + runif(num_x, 0, 0.2)
reg_df <- tibble(x=x_data, y=y_data)
ggplot(reg_df, aes(x=x, y=y)) +
  geom_point(size=g_pointsize) +
  dsan_theme("quarter")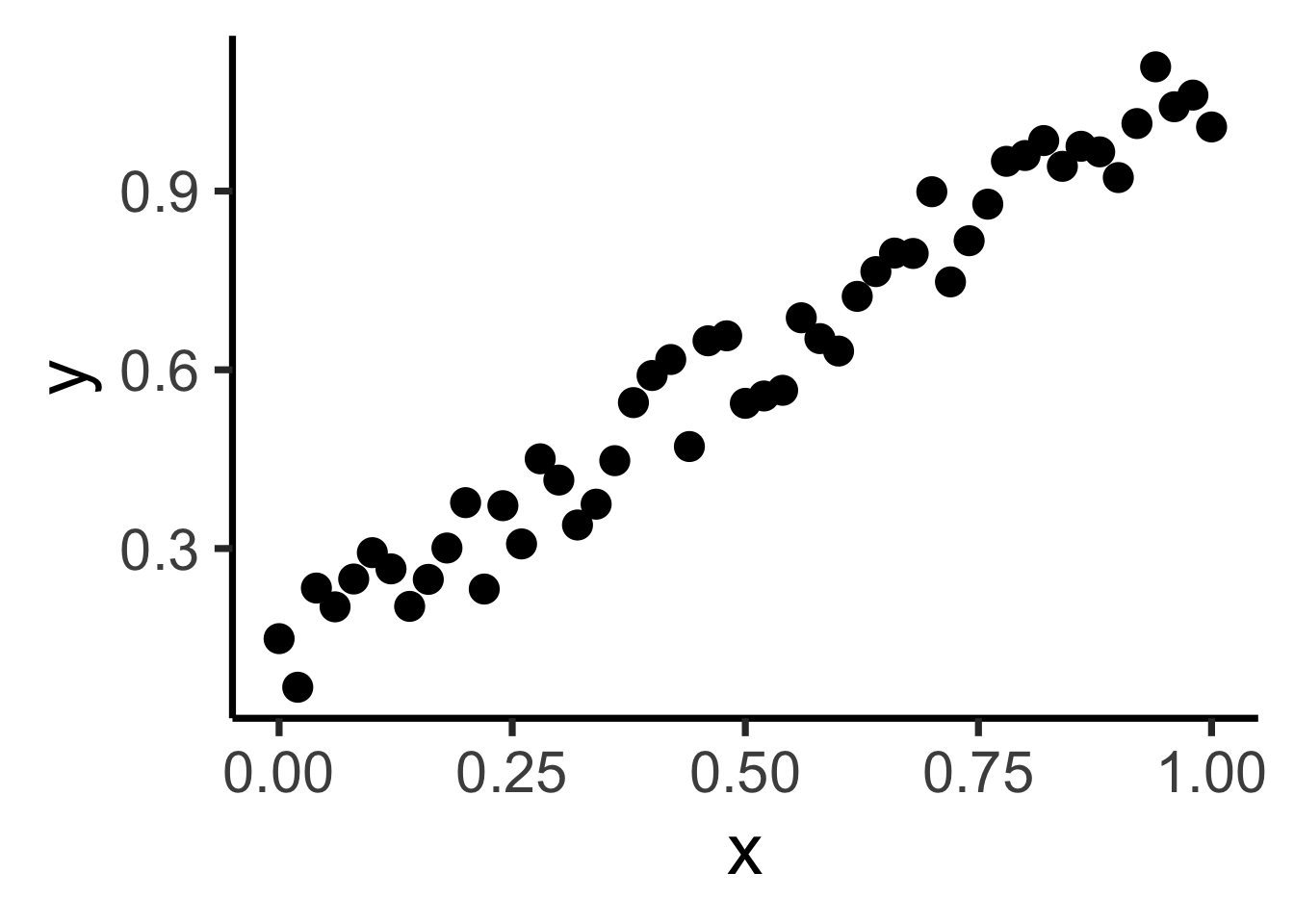

psychology psychology
trending_flat

ggplot(reg_df, aes(x=x, y=y)) + 
  geom_point(size=g_pointsize) +
  geom_smooth(method = "lm", se = FALSE, color = cbPalette[1], formula = y ~ x, linewidth = g_linewidth*3) +
  dsan_theme("quarter")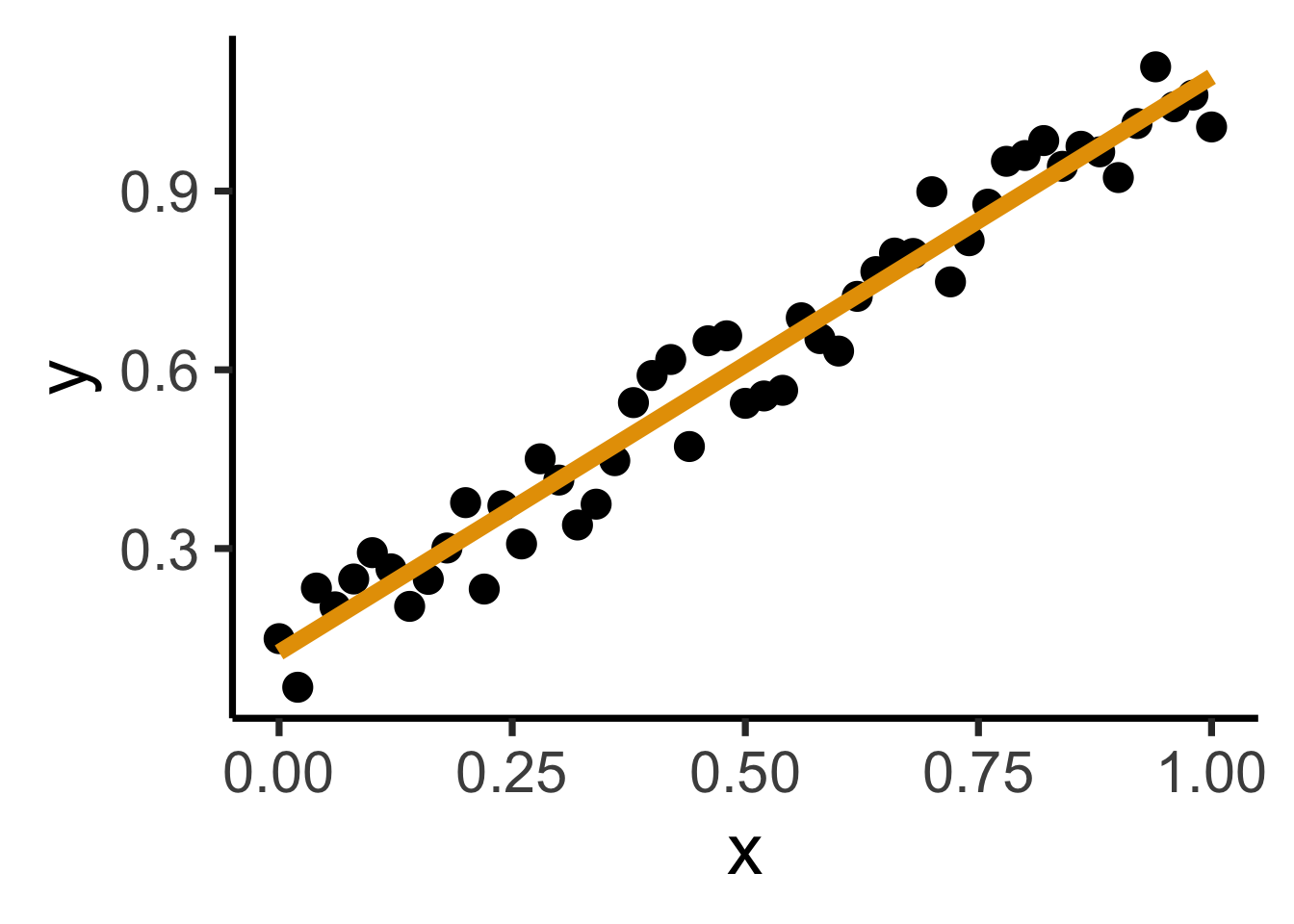

The Goal

• Whenever you carry out a regression, keep the goal in the front of your mind:

The Goal of Regression

Find a line $\hat{y}=mx+b$ that best predicts $Y$ for given values of $X$

How Do We Define “Best”?

• Intuitively, two different ways to measure how well a line fits the data:

N <- 11
x <- seq(from = 0, to = 1, by = 1 / (N - 1))
y <- x + rnorm(N, 0, 0.25)
mean_y <- mean(y)
spread <- y - mean_y
df <- tibble(x = x, y = y, spread = spread)
ggplot(df, aes(x=x, y=y)) +
  geom_abline(slope=1, intercept=0, linetype="dashed", color=cbPalette[1], linewidth=g_linewidth*2) +
  geom_segment(xend=(x+y)/2, yend=(x+y)/2, linewidth=g_linewidth*2, color=cbPalette[2]) +
  geom_point(size=g_pointsize) +
  coord_equal() +
  dsan_theme("half") +
  labs(
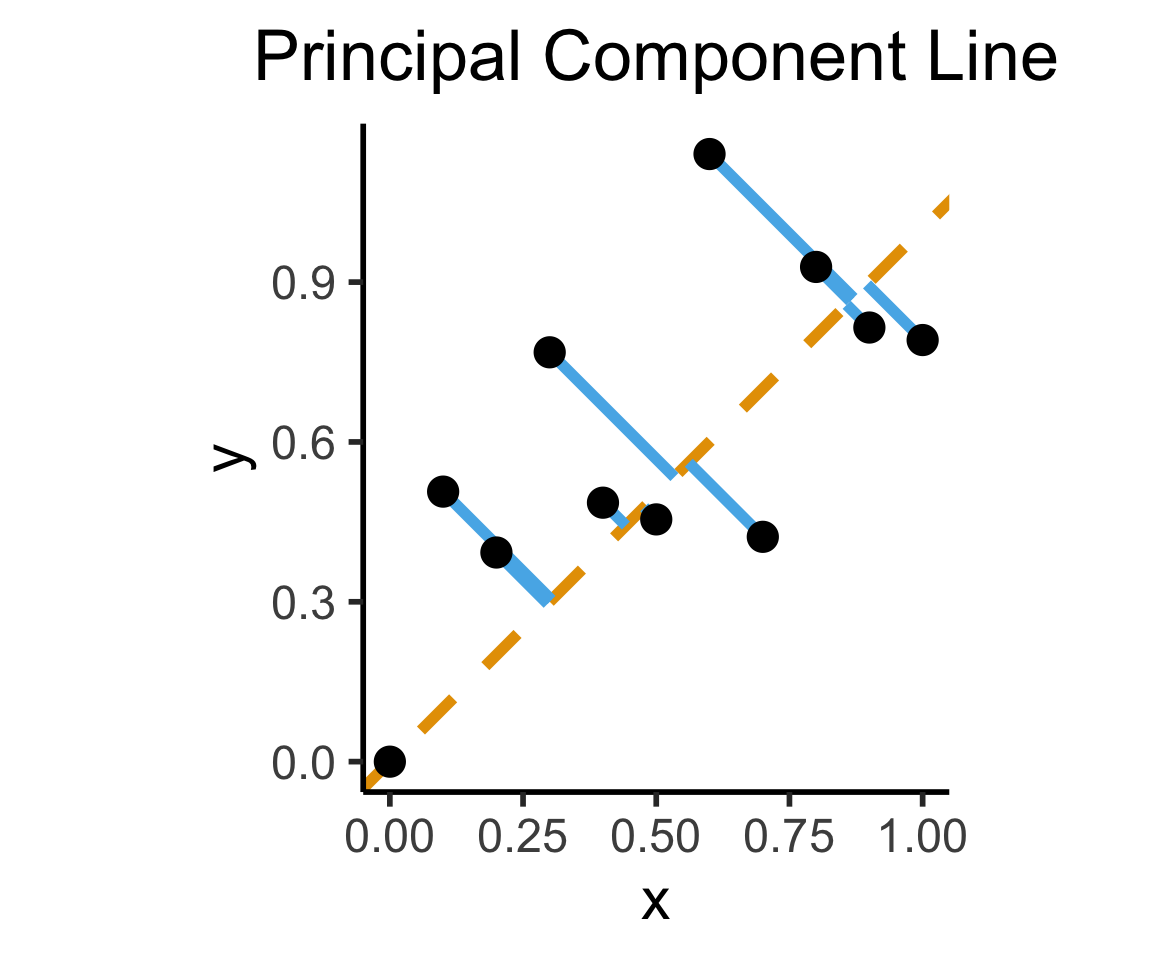
    title = "Principal Component Line"
  )
ggplot(df, aes(x=x, y=y)) +
  geom_abline(slope=1, intercept=0, linetype="dashed", color=cbPalette[1], linewidth=g_linewidth*2) +
  geom_segment(xend=x, yend=x, linewidth=g_linewidth*2, color=cbPalette[2]) +
  geom_point(size=g_pointsize) +
  coord_equal() +
  dsan_theme("half") +
  labs(
    title = "Regression Line"
  )

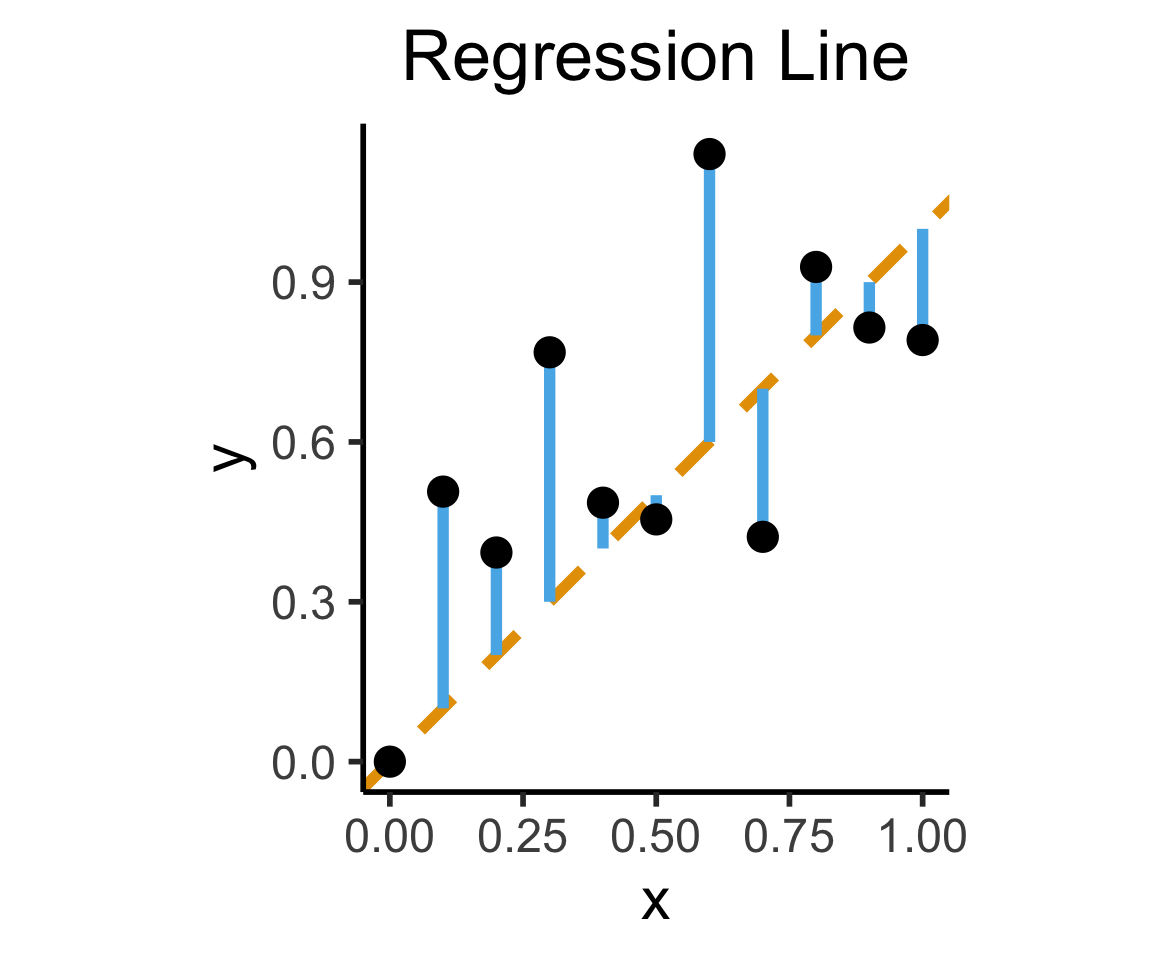
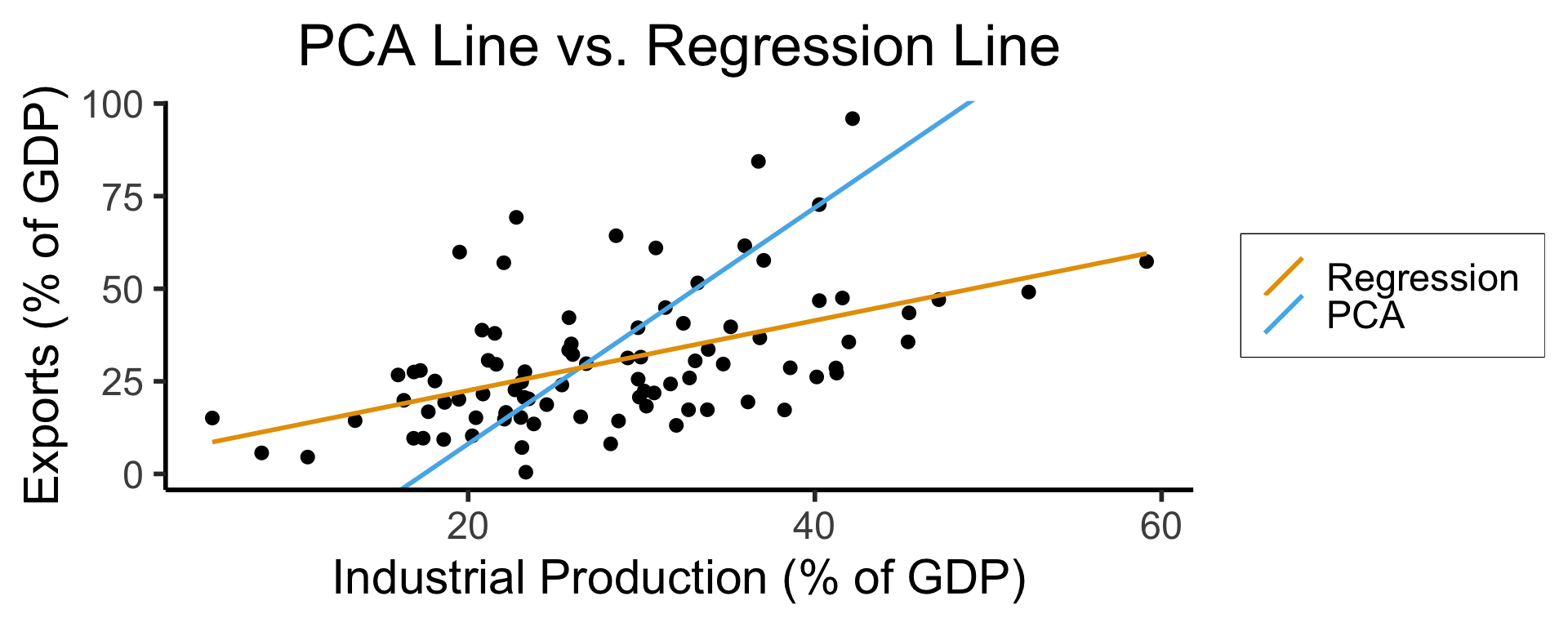
On the difference between these two lines, and why it matters, I cannot recommend Gelman and Hill (2007) enough!

Principal Component Analysis

• Principal Component Line can be used to project the data onto its dimension of highest variance

• More simply: PCA can discover meaningful axes in data (unsupervised learning / exploratory data analysis settings)

library(readr)
library(ggplot2)
gdp_df <- read_csv("assets/gdp_pca.csv")

dist_to_line <- function(x0, y0, a, c) {
    numer <- abs(a * x0 - y0 + c)
    denom <- sqrt(a * a + 1)
    return(numer / denom)
}
# Finding PCA line for industrial vs. exports
x <- gdp_df$industrial
y <- gdp_df$exports
lossFn <- function(lineParams, x0, y0) {
    a <- lineParams[1]
    c <- lineParams[2]
    return(sum(dist_to_line(x0, y0, a, c)))
}
o <- optim(c(0, 0), lossFn, x0 = x, y0 = y)
ggplot(gdp_df, aes(x = industrial, y = exports)) +
    geom_point(size=g_pointsize/2) +
    geom_abline(aes(slope = o$par[1], intercept = o$par[2], color="pca"), linewidth=g_linewidth, show.legend = TRUE) +
    geom_smooth(aes(color="lm"), method = "lm", se = FALSE, linewidth=g_linewidth, key_glyph = "blank") +
    scale_color_manual(element_blank(), values=c("pca"=cbPalette[2],"lm"=cbPalette[1]), labels=c("Regression","PCA")) +
    dsan_theme("half") +
    remove_legend_title() +
    labs(
      title = "PCA Line vs. Regression Line",
        x = "Industrial Production (% of GDP)",
        y = "Exports (% of GDP)"
    )

See https://juliasilge.com/blog/un-voting/ for an amazing blog post using PCA, with 2 dimensions, to explore UN voting patterns!

Create Your Own Dimension!

ggplot(gdp_df, aes(pc1, .fittedPC2)) +
    geom_point(size = g_pointsize/2) +
    geom_hline(aes(yintercept=0, color='PCA Line'), linetype='solid', size=g_linesize) +
    geom_rug(sides = "b", linewidth=g_linewidth/1.2, length = unit(0.1, "npc"), color=cbPalette[3]) +
    expand_limits(y=-1.6) +
    scale_color_manual(element_blank(), values=c("PCA Line"=cbPalette[2])) +
    dsan_theme("full") +
    remove_legend_title() +
    labs(
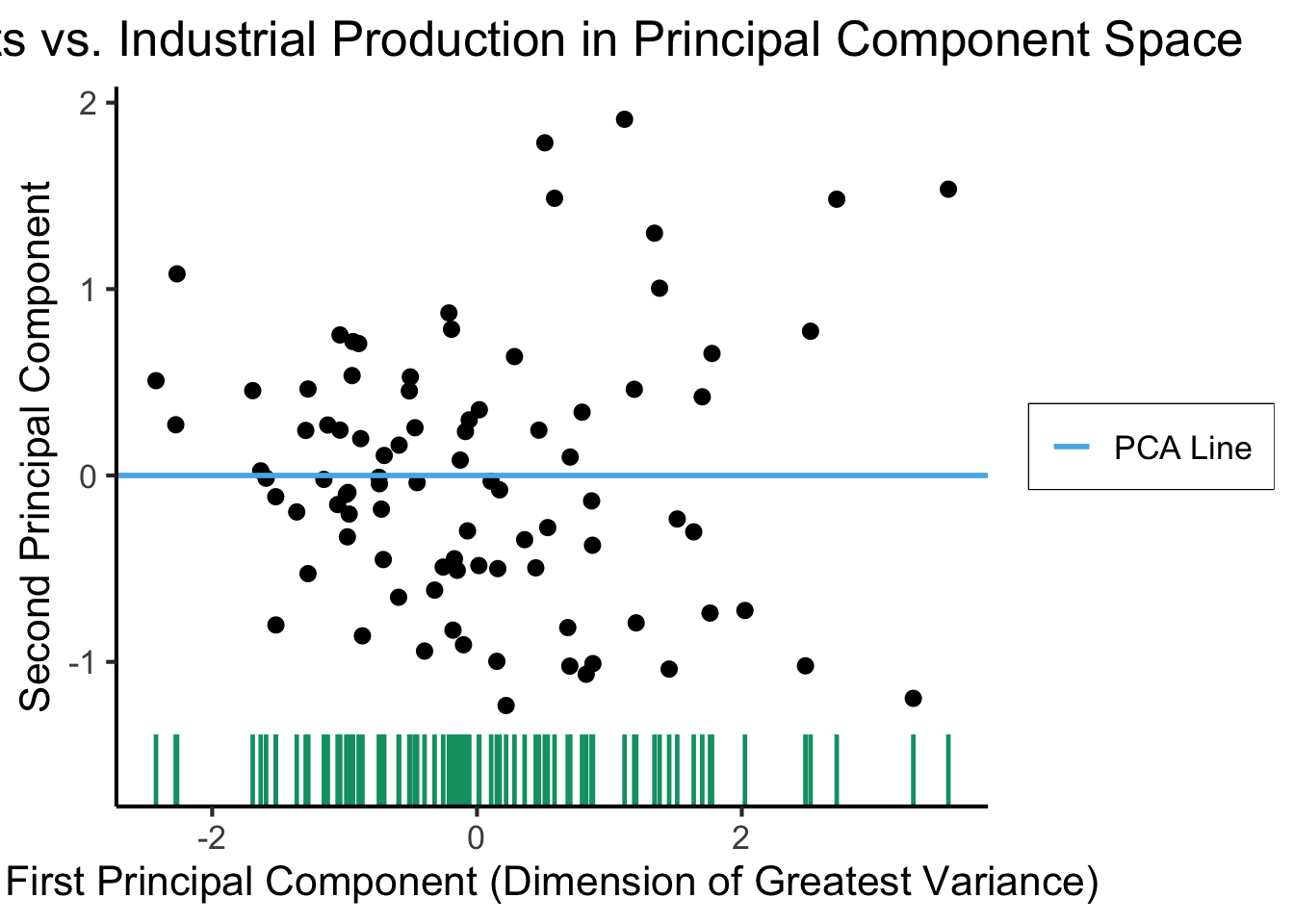
      title = "Exports vs. Industrial Production in Principal Component Space",
      x = "First Principal Component (Dimension of Greatest Variance)",
      y = "Second Principal Component"
    )

And Use It for EDA

library(dplyr)
library(tidyr)
plot_df <- gdp_df %>% select(c(country_code, pc1, agriculture, military))
long_df <- plot_df %>% pivot_longer(!c(country_code, pc1), names_to = "var", values_to = "val")
long_df <- long_df |> mutate(
  var = case_match(
    var,
    "agriculture" ~ "Agricultural Production",
    "military" ~ "Military Spending"
  )
)
ggplot(long_df, aes(x = pc1, y = val, facet = var)) +
    geom_point() +
    facet_wrap(vars(var), scales = "free") +
    dsan_theme("full") +
    labs(
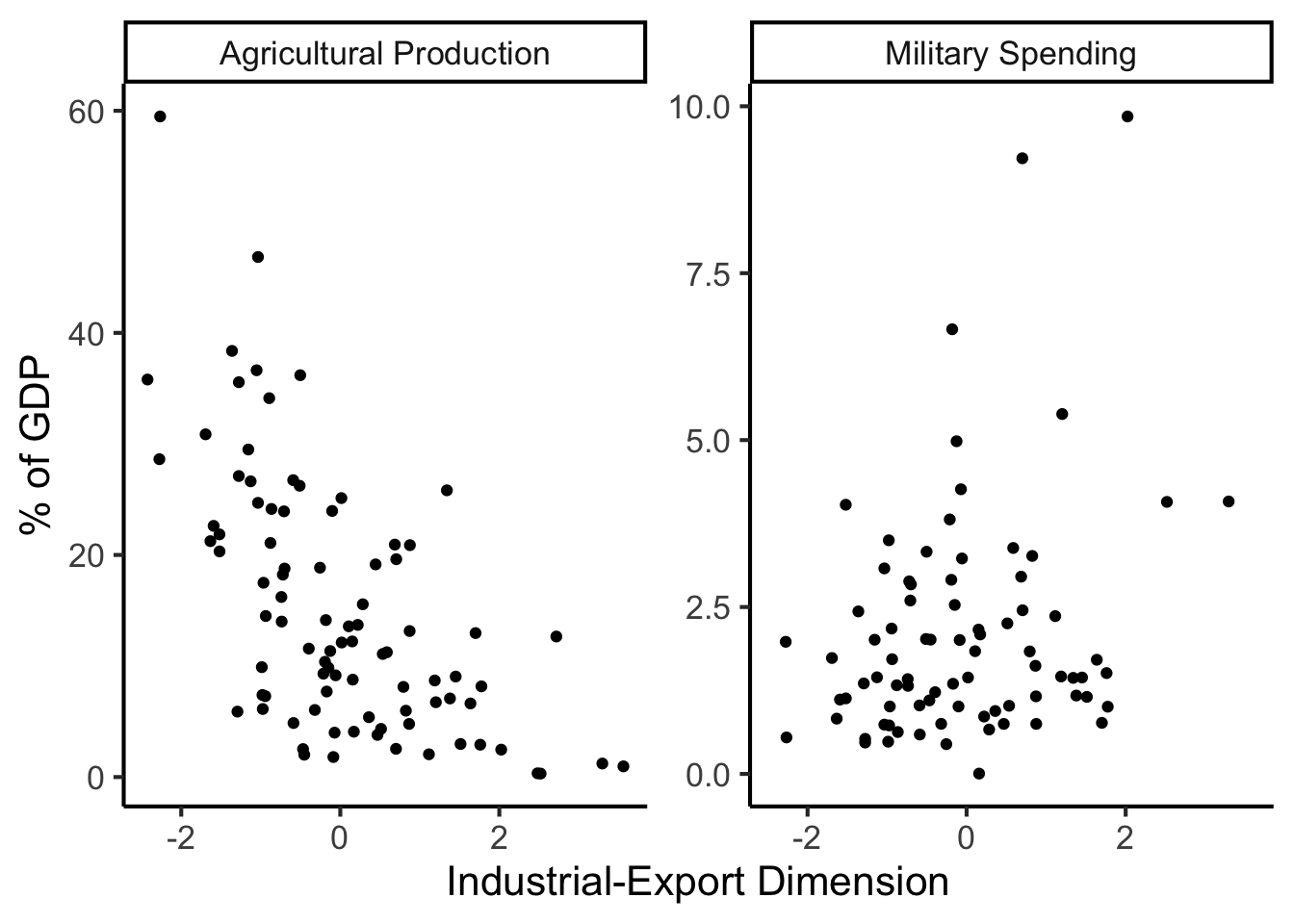
        x = "Industrial-Export Dimension",
        y = "% of GDP"
    )

But in Our Case…

• $x$ and $y$ dimensions already have meaning, and we have a hypothesis about $x\to y$!

The Regression Hypothesis ${\mathcal{H}}_{\text{reg}}$

Given data $(X,Y)$, we estimate $\hat{y}=\widehat{{\beta }_0}+\widehat{{\beta }_1}x$, hypothesizing that:

• Starting from $y=\widehat{{\beta }_0}$ when $x=0$ (the intercept),
• An increase of $x$ by 1 unit is associated with an increase of $y$ by $\widehat{{\beta }_1}$ units (the coefficient)

• We want to measure how well our line predicts $y$ for any given $x$ value $⟹$ vertical distance from regression line

Key Features of Regression Line

• Regression line is BLUE: Best Linear Unbiased Estimator
• What exactly is it the “best” linear estimator of?

$$\hat{y}=\underset{\begin{array}{c}\text{Predicted}\\ \text{intercept}\end{array}}{\underbrace{\widehat{{\beta }_0}}}+\underset{\begin{array}{c}\text{Predicted}\\ \text{slope}\end{array}}{\underbrace{\widehat{{\beta }_1}}}\cdot x$$

is chosen so that

$$\theta =(\widehat{{\beta }_0},\widehat{{\beta }_1})=\underset{{\beta }_0,{\beta }_1}{\mathrm{argmin}}\left[\sum _{x_i\in X}{(\stackrel{\text{Predicted }y}{\overbrace{\hat{y}(x_i)}}-\stackrel{\text{Avg. }y\text{ when }x=x_i}{\overbrace{\mathbb{E}[Y\mid X=x_i]}})}^2\right]$$

Regression in R

lin_model <- lm(military ~ industrial, data=gdp_df)
summary(lin_model)

Call:
lm(formula = military ~ industrial, data = gdp_df)

Residuals:
    Min      1Q  Median      3Q     Max 
-2.3354 -1.0997 -0.3870  0.6081  6.7508 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)  
(Intercept)  0.61969    0.59526   1.041   0.3010  
industrial   0.05253    0.02019   2.602   0.0111 *
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.671 on 79 degrees of freedom
  (8 observations deleted due to missingness)
Multiple R-squared:  0.07895,   Adjusted R-squared:  0.06729 
F-statistic: 6.771 on 1 and 79 DF,  p-value: 0.01106

lm Syntax

lm(
  formula = dependent ~ independent + controls,
  data = my_df
)

Interpreting Output

Call:
lm(formula = military ~ industrial, data = gdp_df)

Residuals:
    Min      1Q  Median      3Q     Max 
-2.3354 -1.0997 -0.3870  0.6081  6.7508 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)  
(Intercept)  0.61969    0.59526   1.041   0.3010  
industrial   0.05253    0.02019   2.602   0.0111 *

---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.671 on 79 degrees of freedom
  (8 observations deleted due to missingness)
Multiple R-squared:  0.07895,   Adjusted R-squared:  0.06729 
F-statistic: 6.771 on 1 and 79 DF,  p-value: 0.01106

Zooming In: Coefficients

	Estimate	Std. Error	t value	Pr(>|t|)
(Intercept)	0.61969	0.59526	1.041	0.3010
industrial	0.05253	0.02019	2.602	0.0111	*
	$\hat{\beta }$	Uncertainty	Test statistic	How extreme is test stat?	Statistical significance

$$\hat{y}\approx \stackrel{{\beta }_0}{\underset{\pm 0.595}{0.620}}+\stackrel{{\beta }_1}{\underset{\pm 0.020}{0.053}}\cdot x$$

Zooming In: Significance

	Estimate	Std. Error	t value	Pr(>|t|)
(Intercept)	0.61969	0.59526	1.041	0.3010
industrial	0.05253	0.02019	2.602	0.0111	*
	$\hat{\beta }$	Uncertainty	Test statistic	How extreme is test stat?	Statistical significance

library(ggplot2)
int_tstat <- 1.041
int_tstat_str <- sprintf("%.02f", int_tstat)
label_df_int <- tribble(
    ~x, ~y, ~label,
    0.25, 0.05, paste0("P(t > ",int_tstat_str,")\n= 0.3")
)
label_df_signif_int <- tribble(
    ~x, ~y, ~label,
    2.7, 0.075, "95% Signif.\nCutoff"
)
funcShaded <- function(x, lower_bound, upper_bound){
    y <- dnorm(x)
    y[x < lower_bound | x > upper_bound] <- NA
    return(y)
}
funcShadedIntercept <- function(x) funcShaded(x, int_tstat, Inf)
funcShadedSignif <- function(x) funcShaded(x, 1.96, Inf)
ggplot(data=data.frame(x=c(-3,3)), aes(x=x)) +
  stat_function(fun=dnorm, linewidth=g_linewidth) +
  geom_vline(aes(xintercept=int_tstat), linewidth=g_linewidth) +
  geom_vline(aes(xintercept = 1.96), linewidth=g_linewidth, linetype="dashed") +
  stat_function(fun = funcShadedIntercept, geom = "area", fill = cbPalette[1], alpha = 0.5) +
  stat_function(fun = funcShadedSignif, geom = "area", fill = "grey", alpha = 0.333) +
  geom_text(label_df_int, mapping = aes(x = x, y = y, label = label), size = 10) +
  geom_text(label_df_signif_int, mapping = aes(x = x, y = y, label = label), size = 8) +
  # Add single additional tick
  scale_x_continuous(breaks=c(-2, 0, int_tstat, 2), labels=c("-2","0",int_tstat_str,"2")) +
  dsan_theme("quarter") +
  labs(
    title = "t Value for Intercept",
    x = "t",
    y = "Density"
  ) +
  theme(axis.text.x = element_text(colour = c("black", "black", cbPalette[1], "black")))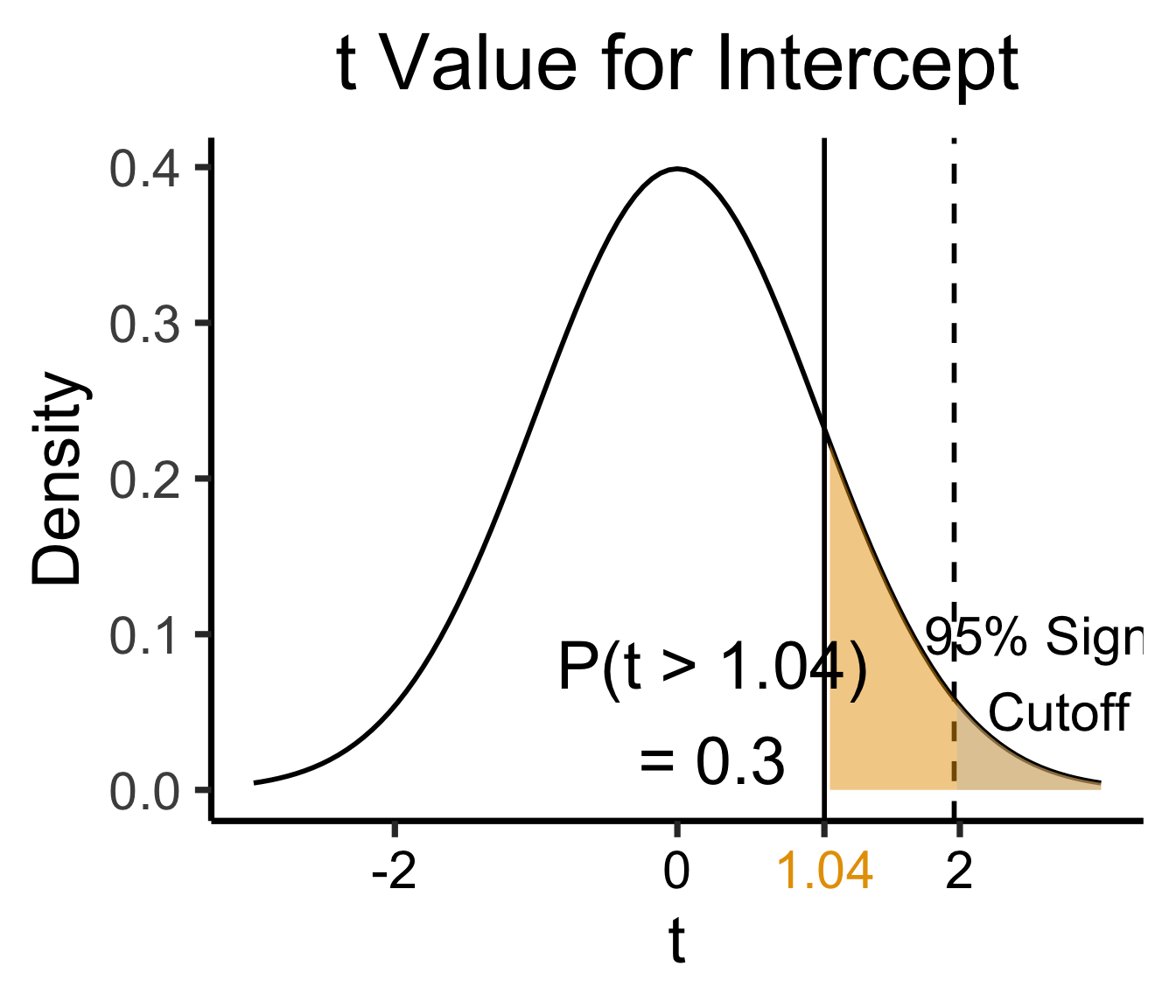

library(ggplot2)
coef_tstat <- 2.602
coef_tstat_str <- sprintf("%.02f", coef_tstat)
label_df_coef <- tribble(
    ~x, ~y, ~label,
    3.65, 0.06, paste0("P(t > ",coef_tstat_str,")\n= 0.01")
)
label_df_signif_coef <- tribble(
  ~x, ~y, ~label,
  1.05, 0.03, "95% Signif.\nCutoff"
)
funcShadedCoef <- function(x) funcShaded(x, coef_tstat, Inf)
ggplot(data=data.frame(x=c(-4,4)), aes(x=x)) +
  stat_function(fun=dnorm, linewidth=g_linewidth) +
  geom_vline(aes(xintercept=coef_tstat), linetype="solid", linewidth=g_linewidth) +
  geom_vline(aes(xintercept=1.96), linetype="dashed", linewidth=g_linewidth) +
  stat_function(fun = funcShadedCoef, geom = "area", fill = cbPalette[2], alpha = 0.5) +
  stat_function(fun = funcShadedSignif, geom = "area", fill = "grey", alpha = 0.333) +
  # Label shaded area
  geom_text(label_df_coef, mapping = aes(x = x, y = y, label = label), size = 10) +
  # Label significance cutoff
  geom_text(label_df_signif_coef, mapping = aes(x = x, y = y, label = label), size = 8) +
  coord_cartesian(clip = "off") +
  # Add single additional tick
  scale_x_continuous(breaks=c(-4, -2, 0, 2, coef_tstat, 4), labels=c("-4", "-2","0", "2", coef_tstat_str,"4")) +
  dsan_theme("quarter") +
  labs(
    title = "t Value for Coefficient",
    x = "t",
    y = "Density"
  ) +
  theme(axis.text.x = element_text(colour = c("black", "black", "black", "black", cbPalette[2], "black")))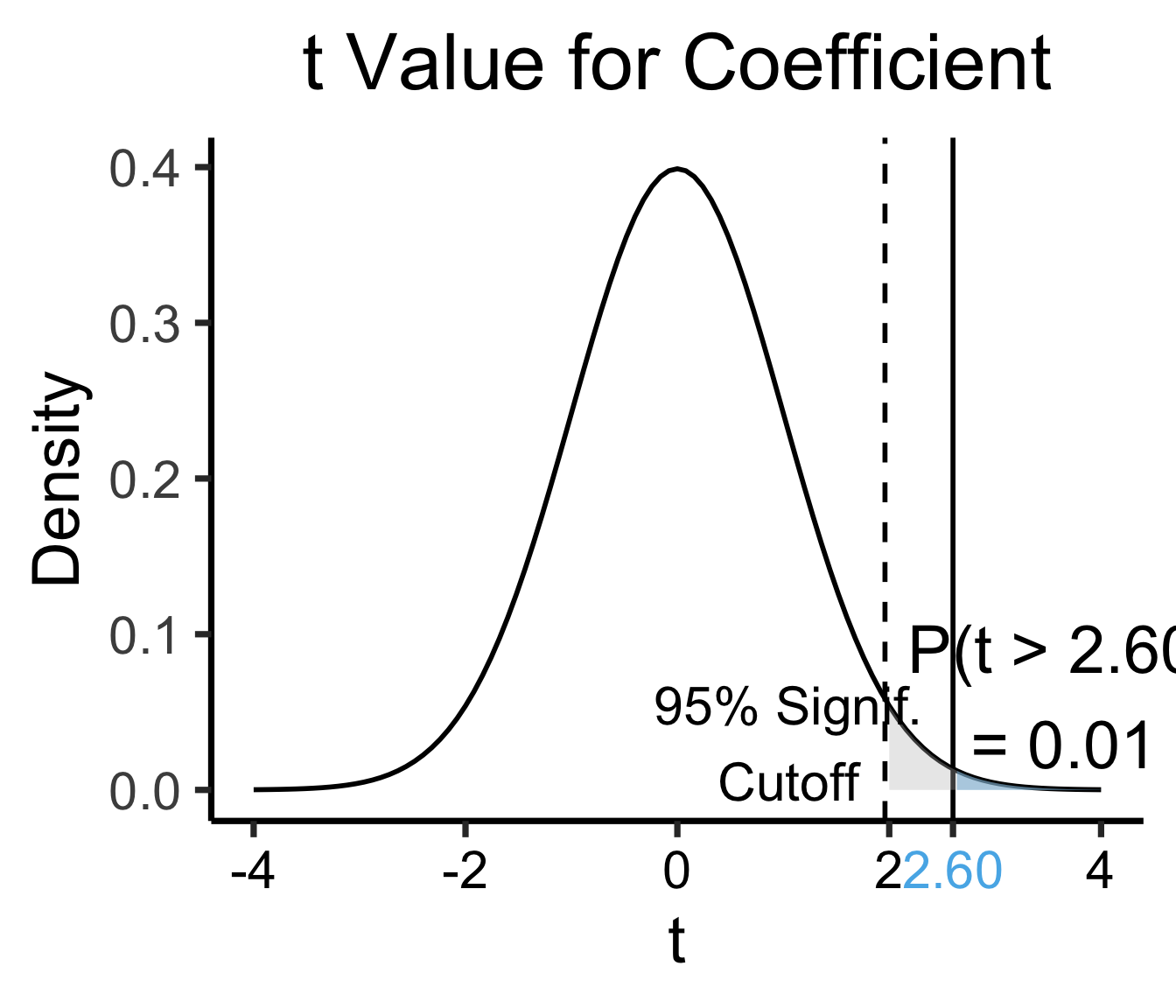

The Residual Plot

• A key assumption required for OLS: “homoskedasticity”
• Given our model $$y_i={\beta }_0+{\beta }_1{x}_i+{\epsilon }_i$$ the errors ${\epsilon }_i$ should not vary systematically with $i$
• Formally: $\mathrm{\forall }i[\text{Var}[{\epsilon }_i]={\sigma }^2]$

library(broom)
gdp_resid_df <- augment(lin_model)
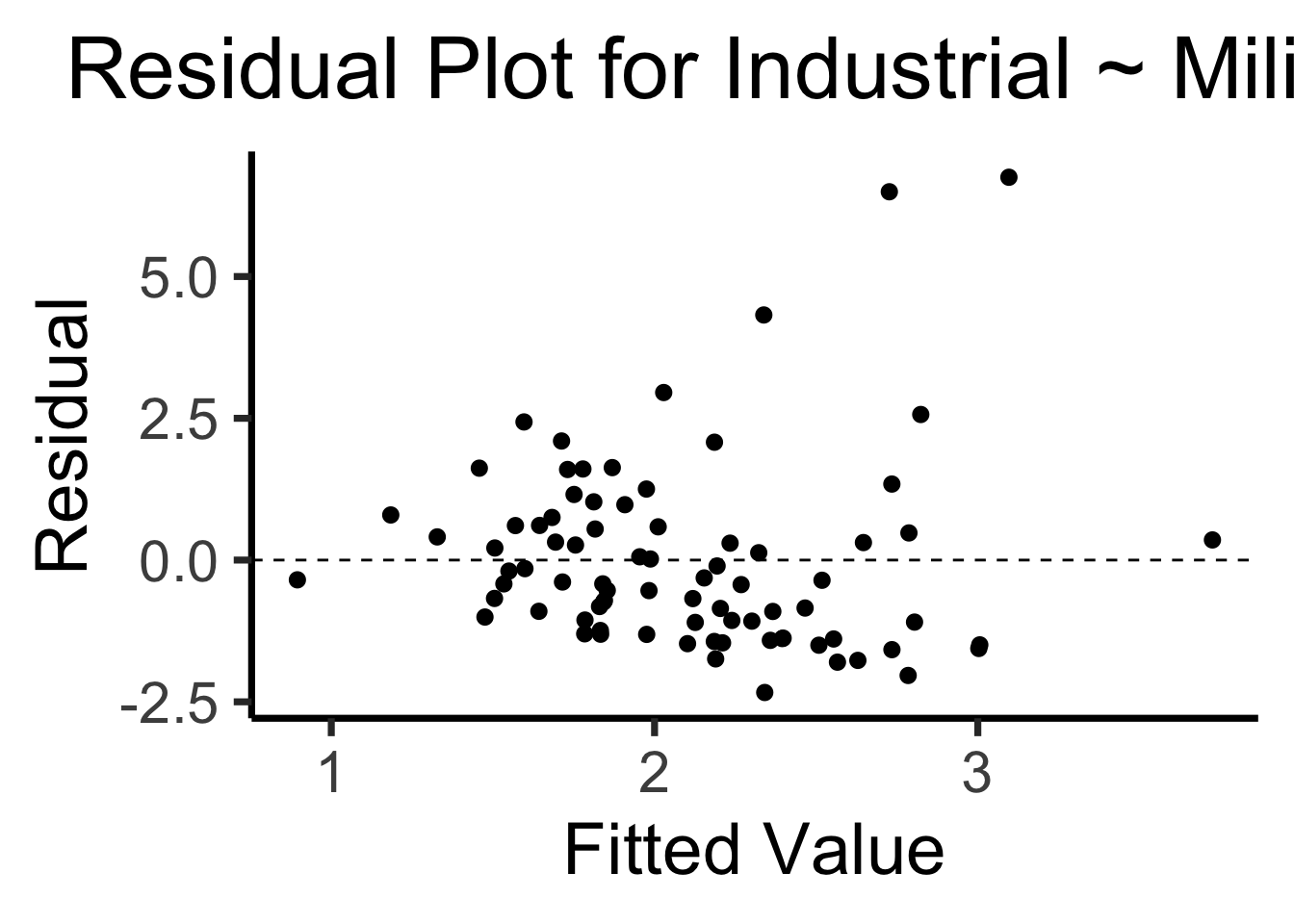
ggplot(gdp_resid_df, aes(x = .fitted, y = .resid)) +
    geom_point(size = g_pointsize/2) +
    geom_hline(yintercept=0, linetype="dashed") +
    dsan_theme("quarter") +
    labs(
      title = "Residual Plot for Industrial ~ Military",
      x = "Fitted Value",
      y = "Residual"
    )

x <- 1:80
errors <- rnorm(length(x), 0, x^2/1000)
y <- x + errors
het_model <- lm(y ~ x)
df_het <- augment(het_model)
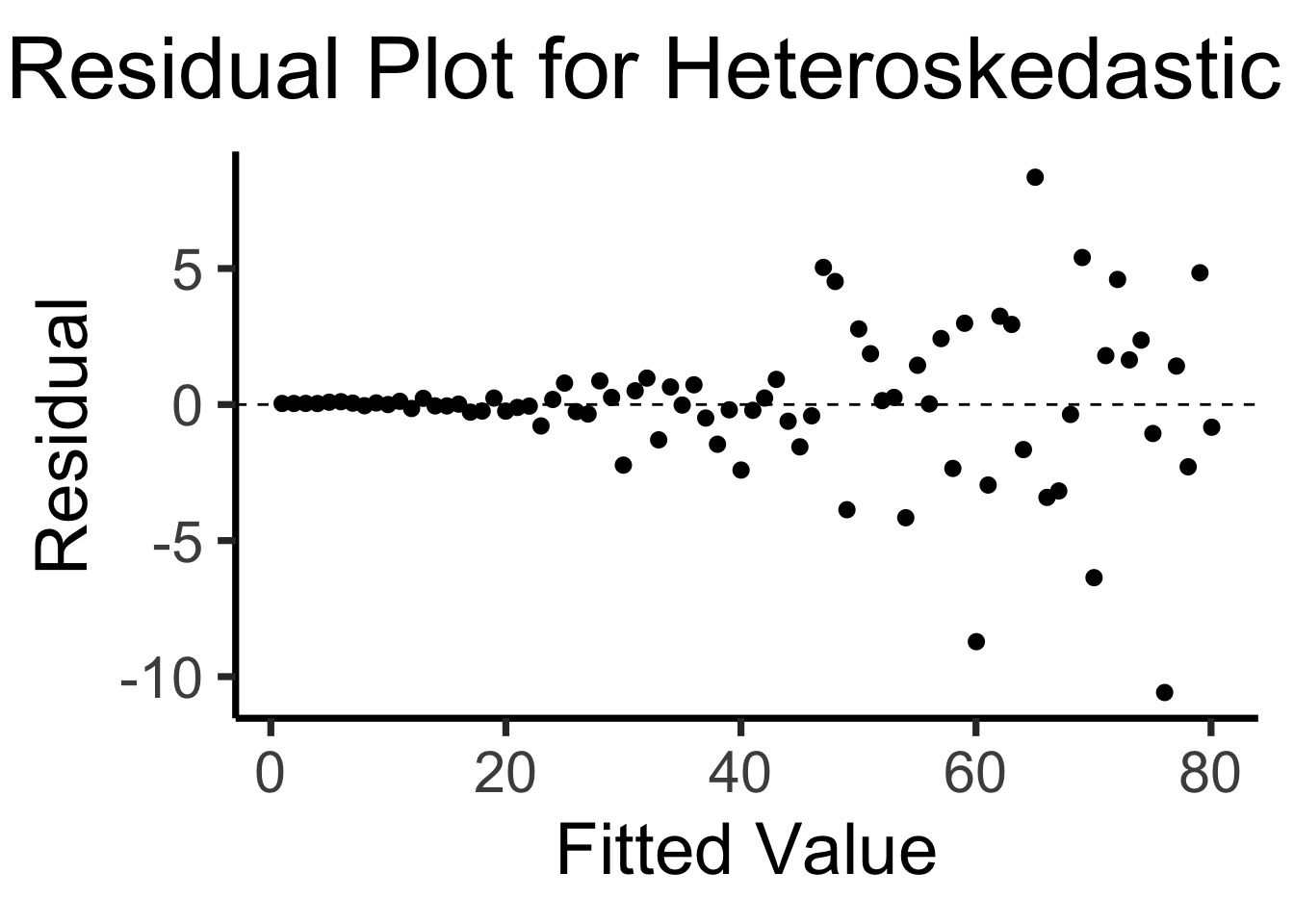
ggplot(df_het, aes(x = .fitted, y = .resid)) +
    geom_point(size = g_pointsize / 2) +
    geom_hline(yintercept = 0, linetype = "dashed") +
    dsan_theme("quarter") +
    labs(
        title = "Residual Plot for Heteroskedastic Data",
        x = "Fitted Value",
        y = "Residual"
    )

Q-Q Plot

• If $(\hat{y}-y)\sim \mathcal{N}(0,{\sigma }^2)$, points would lie on 45° line:

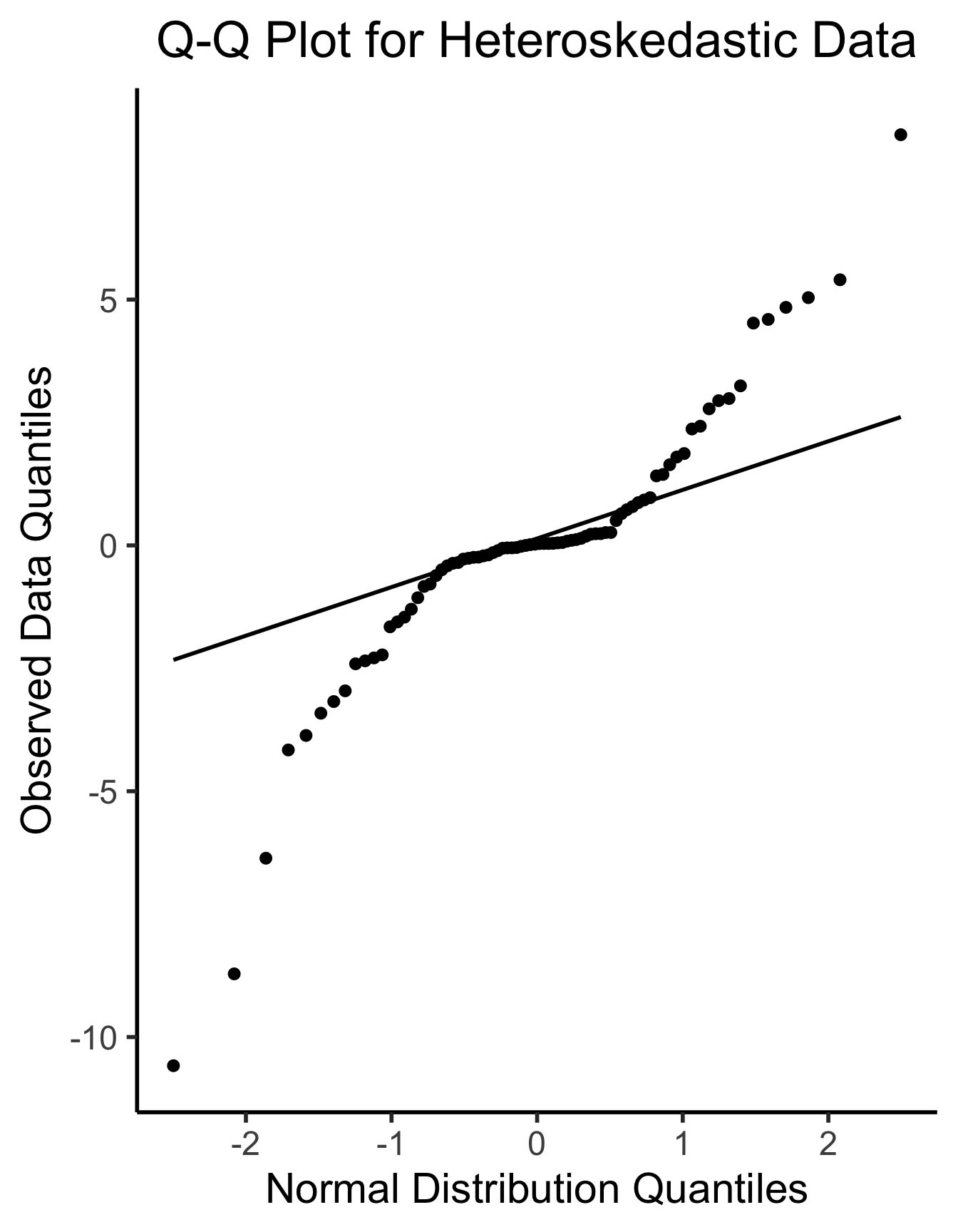
ggplot(df_het, aes(sample=.resid)) +
  stat_qq(size = g_pointsize/2) + stat_qq_line(linewidth = g_linewidth) +
  dsan_theme("half") +
  labs(
    title = "Q-Q Plot for Heteroskedastic Data",
    x = "Normal Distribution Quantiles",
    y = "Observed Data Quantiles"
  )

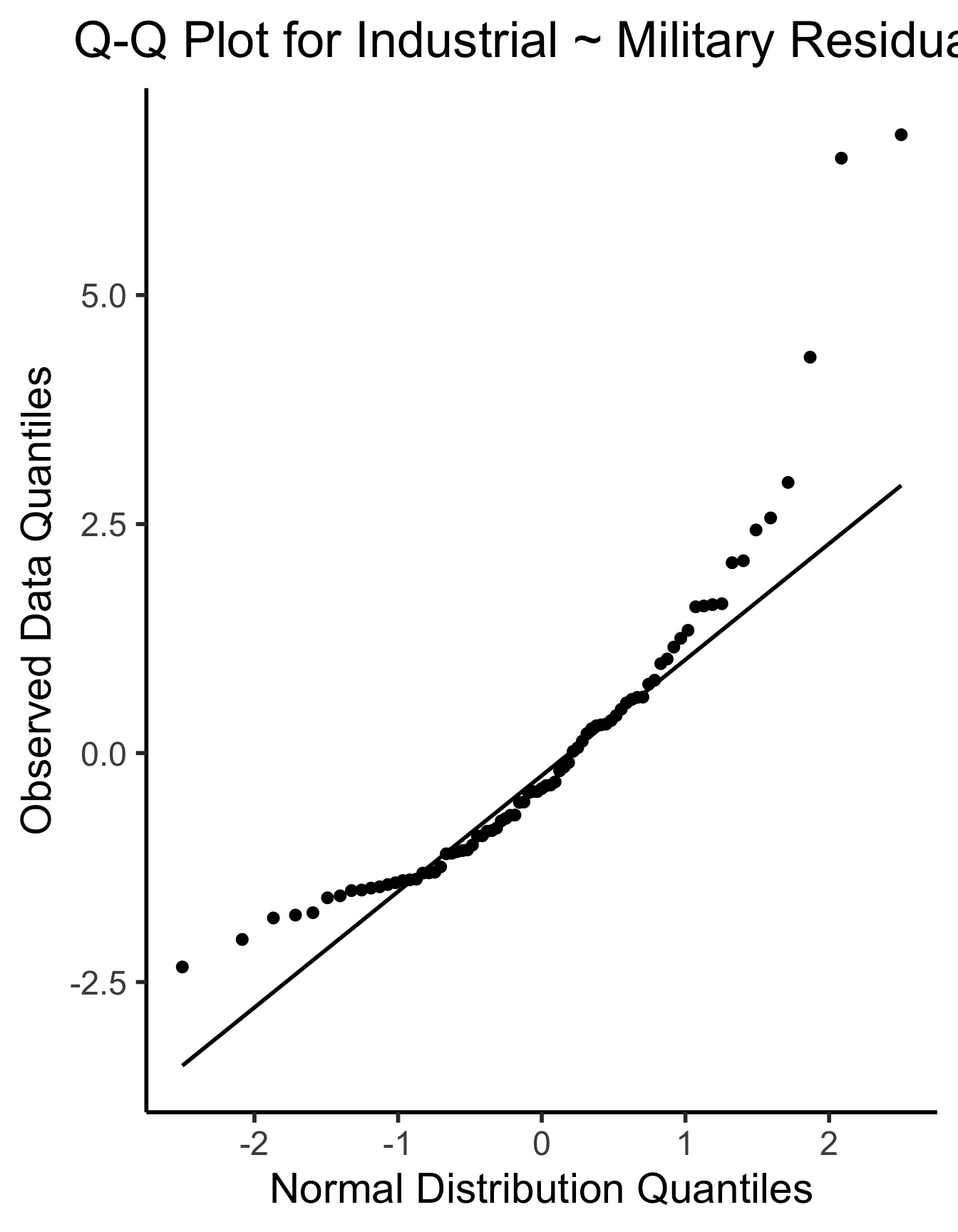
ggplot(gdp_resid_df, aes(sample=.resid)) +
  stat_qq(size = g_pointsize/2) + stat_qq_line(linewidth = g_linewidth) +
  dsan_theme("half") +
  labs(
    title = "Q-Q Plot for Industrial ~ Military Residuals",
    x = "Normal Distribution Quantiles",
    y = "Observed Data Quantiles"
  )

Multiple Linear Regression

• Notation: $x_{i,j}$ = value of independent variable $j$ for person/observation $i$
• $M$ = total number of independent variables

$${\hat{y}}_i={\beta }_0+{\beta }_1{x}_{i,1}+{\beta }_2{x}_{i,2}+\cdots +{\beta }_M{x}_{i,M}$$

• ${\beta }_j$ interpretation: a one-unit increase in $x_{i,j}$ is associated with a ${\beta }_j$ unit increase in $y_i$, holding all other independent variables constant

References

Gelman, Andrew, and Jennifer Hill. 2007. Data Analysis Using Regression and Multilevel/Hierarchical Models. Cambridge University Press.