Week 4: Continuous Distributions

DSAN 5100: Probabilistic Modeling and Statistical Computing
Section 01

Purna Gamage, Amineh Zadbood, and Jeff Jacobs

Tuesday, September 16, 2025

Probability Distributions in General

Discrete vs. Continuous

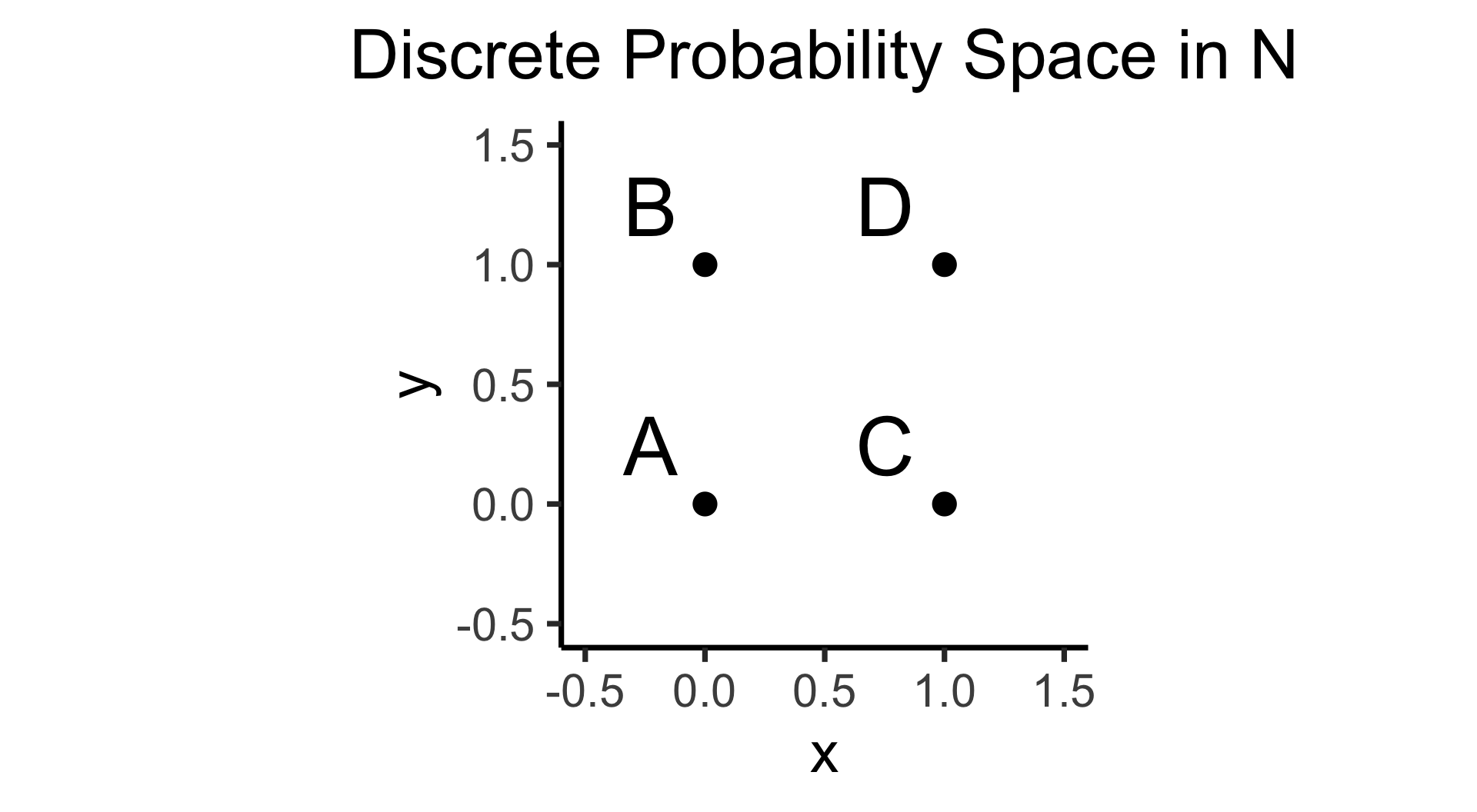
  • Discrete = “Easy mode”: Based (intuitively) on sets
  • \(\Pr(A)\): Four equally-likely marbles \(\{A, B, C, D\}\) in box, what is probability I pull out \(A\)?

\[ \Pr(A) = \underset{\mathclap{\small \text{Probability }\textbf{mass}}}{\boxed{\frac{|\{A\}|}{|\Omega|}}} = \frac{1}{|\{A,B,C,D\}|} = \frac{1}{4} \]

  • Continuous = “Hard mode”: Based (intuitively) on areas
  • \(\Pr(A)\): Throw dart at random point in square, what is probability I hit \(\require{enclose}\enclose{circle}{\textsf{A}}\)?

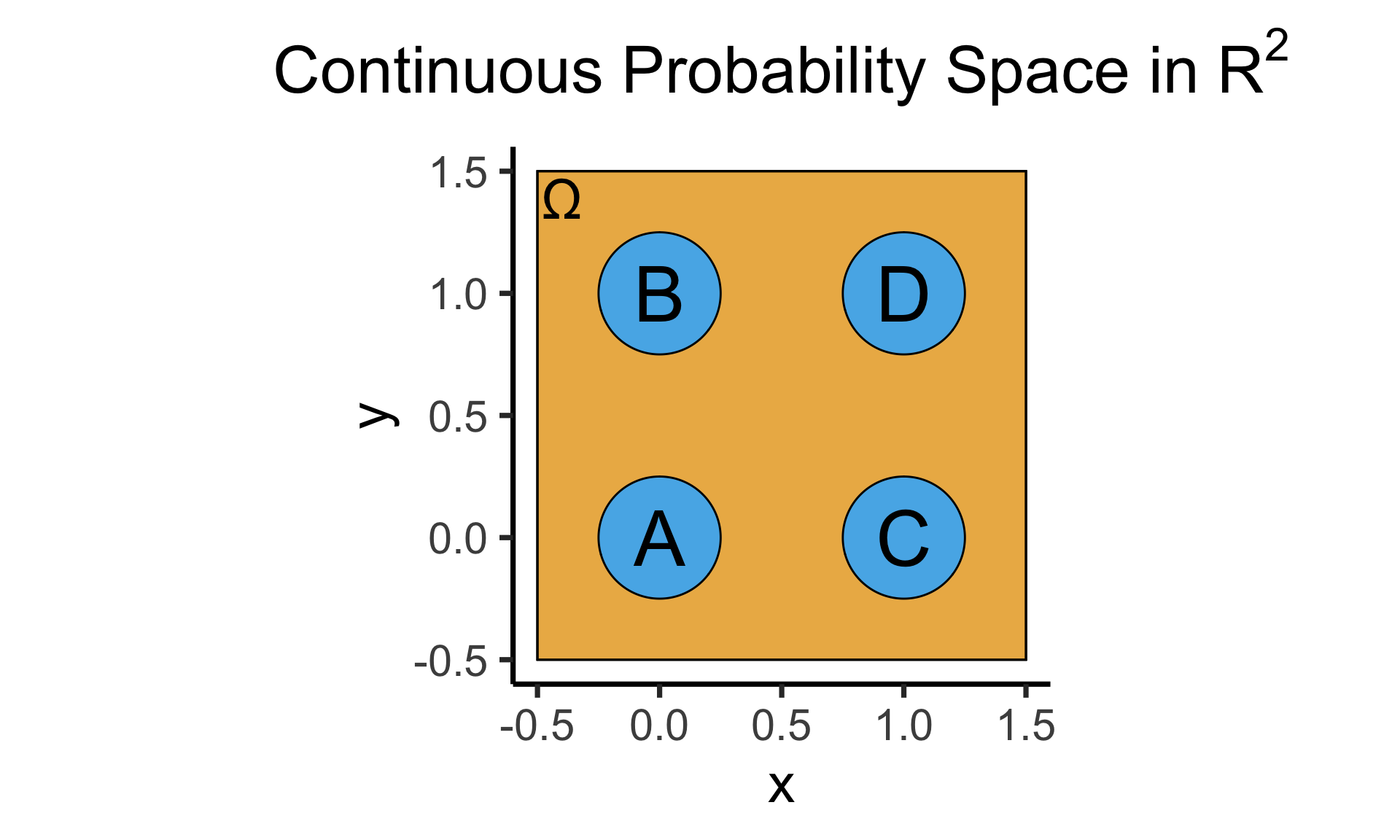
\[ \Pr(A) = \underset{\mathclap{\small \text{Probability }\textbf{density}}}{\boxed{\frac{\text{Area}(\{A\})}{\text{Area}(\Omega)}}} = \frac{\pi r^2}{s^2} = \frac{\pi \left(\frac{1}{4}\right)^2}{4} = \frac{\pi}{64} \]

The Technical Difference tl;dr

  • Countable Sets: Can be put into 1-to-1 correspondence with natural numbers \(\mathbb{N}\)
    • What are you doing when you’re counting? Saying “first”, “second”, “third”, …
    • You’re pairing each object with a natural number! \(\{(\texttt{a},1),(\texttt{b},2),\ldots,(\texttt{z},26)\}\)
  • Uncountable Sets: Can’t be put into 1-to-1 correspondence with natural numbers.
  • \(\mathbb{R}\) is uncountable. Intuition: Try counting the real numbers. Proof \[ \text{Assume }\exists \, (f: \mathbb{R} \leftrightarrow \mathbb{N}): \begin{array}{|c|c|c|c|c|c|c|}\hline \mathbb{R} & & & & & & \Leftrightarrow \mathbb{N} \\ \hline \color{orange}{3} & . & 1 & 4 & 1 & \cdots & \Leftrightarrow 1 \\\hline 4 & . & \color{orange}{9} & 9 & 9 & \cdots & \Leftrightarrow 2 \\\hline 0 & . & 1 & \color{orange}{2} & 3 & \cdots &\Leftrightarrow 3 \\\hline 1 & . & 2 & 3 & \color{orange}{4} & \cdots & \Leftrightarrow 4 \\\hline \vdots & \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\\hline \end{array} \overset{\color{blue}{y_{[i]}} = \color{orange}{x_{[i]}} \overset{\mathbb{Z}_{10}}{+} 1}{\underset{😈}{\longrightarrow}} \color{blue}{y = 4.035 \ldots} \Leftrightarrow \; ? \]

The Practical Difference

  • This part of the course (discrete probability): \(\Pr(X = v), v \in \mathcal{R}_X \subseteq \mathbb{N}\)
    • Example: \(\Pr(\)\() = \Pr(X = 3), 3 \in \{1,2,3,4,5,6\} \subseteq \mathbb{N}\)
  • Next part of the course (continuous probability): \(\Pr(X \in V), V \subseteq \mathbb{R}\)
    • Example: \(\Pr(X \geq 2\pi) = \Pr(X \in [\pi,\infty)), [\pi,\infty) \subseteq \mathbb{R}\)
  • Why do they have to be in separate parts?

\[ \Pr(X \underset{\substack{\uparrow \\ 🚩}}{=} 2\pi) = \frac{\text{Area}(\overbrace{2\pi}^{\mathclap{\small \text{Single point}}})}{\text{Area}(\underbrace{\mathbb{R}}_{\mathclap{\small \text{(Uncountably) Infinite set of points}}})} = 0 \]

The CDF Unifies the Two Worlds!

  • Cumulative Distribution Function (CDF): \(F_X(v) = \Pr(X \leq v)\)1
  • For discrete RV \(X\) (\(\mathcal{R}_X \cong \mathbb{N}\)), Probability Mass Function (pmf) \(p_X(v)\): \[ \begin{align*} p_X(v) &\definedas \Delta F_X(v) \definedas F_X(v) - F_X(v - 1) = \underset{\text{Meaningful}}{\boxed{\Pr(X = v)}} \\ \implies F_X(v) &= \sum_{\{w \in \mathcal{R}_X: \; w \leq v\}}p_X(w) = \underset{\text{Meaningful}}{\boxed{\Pr(X \leq v)}} \end{align*} \]
  • For continuous RV \(X\) (\(\mathcal{R}_X \subseteq \mathbb{R}\)), Probability Density Function (pdf) \(f_X(v)\): \[ \begin{align*} f_X(v) &\definedas \frac{d}{dx}F_X(v) \definedas \lim_{h \rightarrow 0}\frac{F(x + h) - F(x)}{h} = \underset{\text{Not Meaningful}}{\boxed{\; ? \;}} \\ \implies F_X(v) &= \int_{-\infty}^v f_X(w)dw = \underset{\text{Meaningful}}{\boxed{\Pr(X \leq v)}} \end{align*} \]

Probability Density \(\neq\) Probability

  • ☠️BEWARE☠️: \(f_X(v) \neq \Pr(X = v)\)!
  • Long story short, for continuous variables, \(\Pr(X = v)\) is just always \(0\)[^measurezero]
  • Hence, we instead construct a pdf \(f_X(v)\) whose sole purpose is to allow us to calculate \(\Pr(X \in [a,b])\) by integrating!
    • \(f_X(v)\) is whatever satisfies \(\Pr(X \in [a,b]) = \int_{a}^bf_X(v)dv\), and nothing more
  • i.e., instead of \(p_X(v) = \Pr(X = v)\) from discrete world, the relevant function here is \(f_X(v)\), the probability density of \(X\) at \(v\).
Scary math zone
  • For intuition: think of \(X \sim \mathcal{U}(0,10) \implies \Pr(X = \pi) = \frac{|\{v \in \mathbb{R}:\; v = \pi\}|}{|\mathbb{R}|} = \frac{1}{2^{\aleph_0}} \approx 0\). That is, finding the \(\pi\) needle in the \(\mathbb{R}\) haystack is a one-in-\(\left(\infty^\infty\right)\) event.
  • Issue even if \(\mathcal{R}_X\) countably infinite, like \(\mathcal{R}_X = \mathbb{N}\): \(\Pr(X = 3) = \frac{|\{x \in \mathbb{N} : \; x = 3\}|}{|\mathbb{N}|} = \frac{1}{\aleph_0}\). Finding the \(3\) needle in the \(\mathbb{N}\) haystack is a one-in-\(\infty\) event

Common Discrete Distributions

  • Bernoulli
  • Binomial
  • Geometric

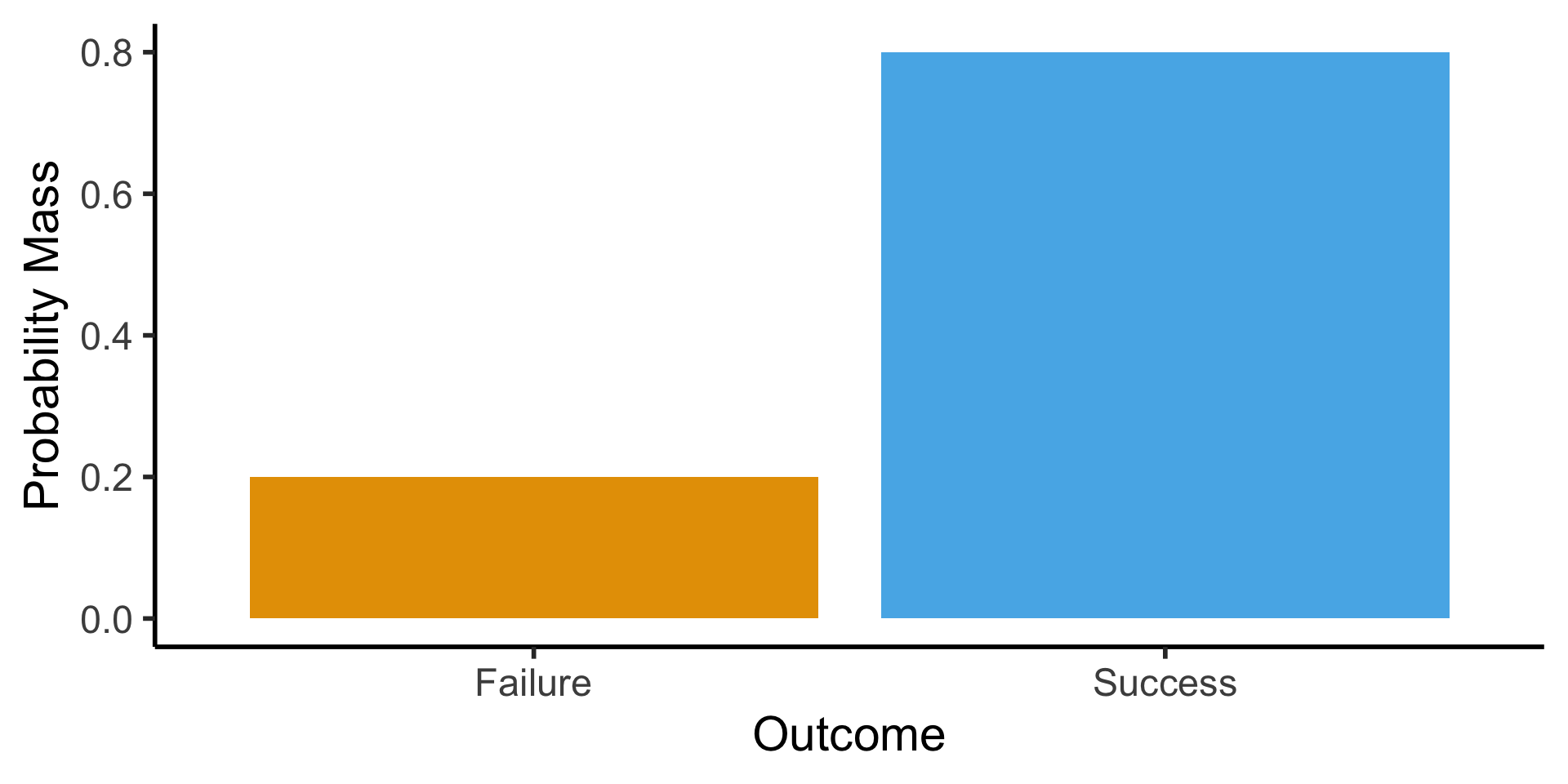
Bernoulli Distribution

  • Single trial with two outcomes, “success” (1) or “failure” (0): basic model of a coin flip (heads = 1, tails = 0)
  • \(X \sim \text{Bern}({\color{purple} p}) \implies \mathcal{R}_X = \{0,1\}, \; \Pr(X = 1) = {\color{purple}p}\).

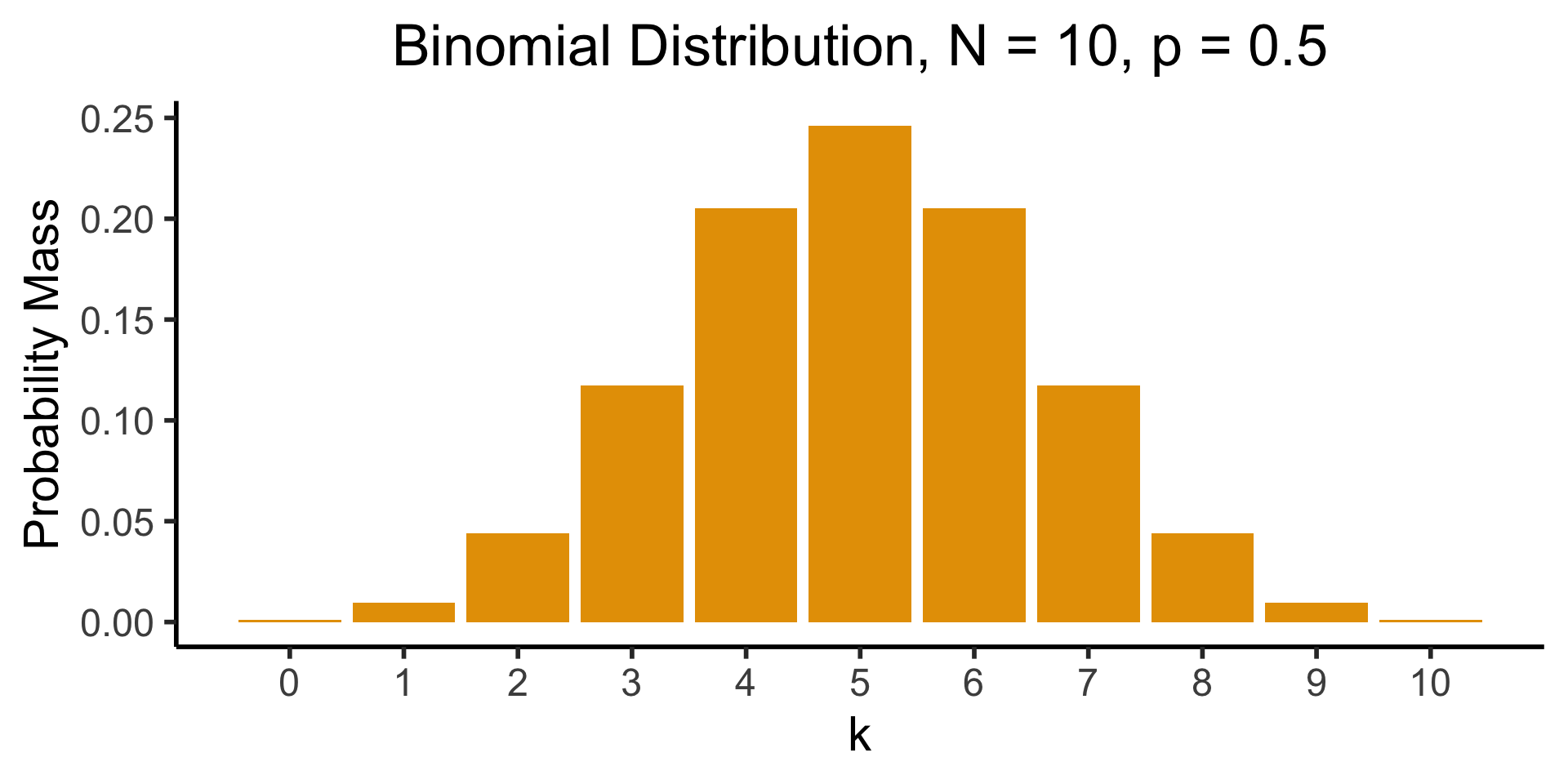
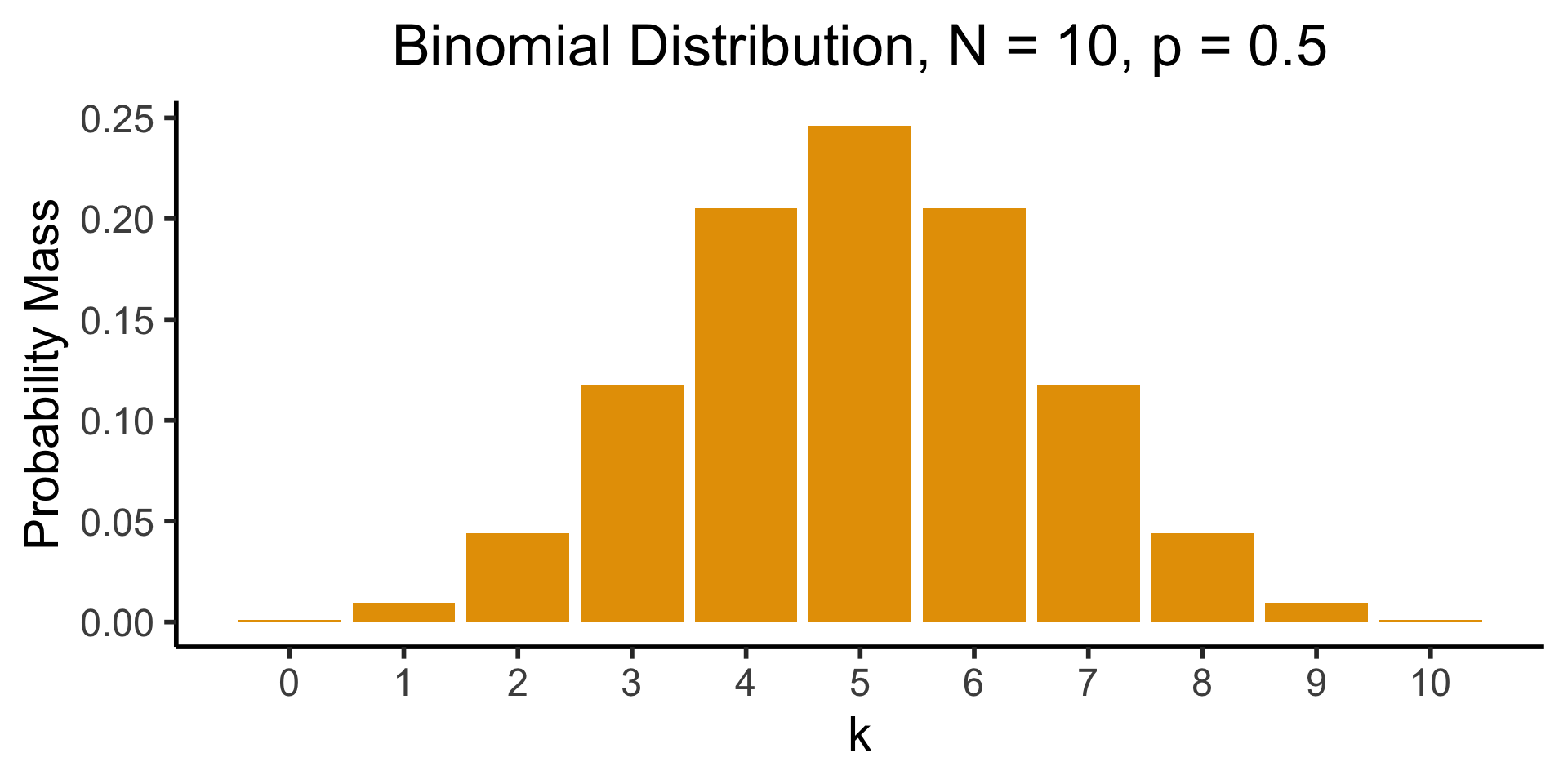
Binomial Distribution

  • Number of successes in \({\color{purple}N}\) Bernoulli trials. \(X \sim \text{Binom}({\color{purple}N},{\color{purple}k},{\color{purple}p}) \implies \mathcal{R}_X = \{0, 1, \ldots, N\}\)
    • \(\Pr(X = k) = \binom{N}{k}p^k(1-p)^{N-k}\): probability of \(k\) successes out of \(N\) trials.
    • \(\binom{N}{k} = \frac{N!}{k!(N-k)!}\): “Binomial coefficient”. How many groups of size \(k\) can be formed?1

Visualizing the Binomial

Code 
k <- seq(0, 10)
prob <- dbinom(k, 10, 0.5)
bar_data <- tibble(k, prob)
ggplot(bar_data, aes(x=k, y=prob)) +
  geom_bar(stat="identity", fill=cbPalette[1]) +
  labs(
    title="Binomial Distribution, N = 10, p = 0.5",
    y="Probability Mass"
  ) +
  scale_x_continuous(breaks=seq(0,10)) +
  dsan_theme("half")

Multiple Classes: Multinomial Distribution

  • Bernoulli only allows two outcomes: success or failure.
  • What if we’re predicting soccer match outcomes?
    • \(X_i \in \{\text{Win}, \text{Loss}, \text{Draw}\}\)
  • Categorical Distribution: Generalizes Bernoulli to \(k\) possible outcomes. \(X \sim \text{Categorical}(\mathbf{p} = \{p_1, p_2, \ldots, p_k\}), \sum_{i=1}^kp_i = 1\).
    • \(\Pr(X = k) = p_k\)
  • Multinomial Distribution: Generalizes Binomial to \(k\) possible outcomes.
  • \(\mathbf{X} \sim \text{Multinom}(N,k,\mathbf{p}=\{p_1,p_2,\ldots,p_k\}), \sum_{i=1}^kp_i=1\)
    • \(\Pr(\mathbf{X} = \{x_1,x_2\ldots,x_k\}) = \frac{N!}{x_1!x_2!\cdots x_k!}p_1^{x_1}p_2^{x_2}\cdots p_k^{x_k}\)
    • \(\Pr(\text{30 wins}, \text{4 losses}, \text{4 draws}) = \frac{38!}{30!4!4!}p_{\text{win}}^{30}p_{\text{lose}}^4p_{\text{draw}}^4\).
    • \(\leadsto\) “Multinomial Coefficient”: \(\binom{38}{30,4,4} = \frac{38!}{30!4!4!}\)

Geometric Distribution

  • Likelihood that we need \({\color{purple}k}\) trials to get our first success. \(X \sim \text{Geom}({\color{purple}k},{\color{purple}p}) \implies \mathcal{R}_X = \{1, 2, \ldots\}\)
    • \(\Pr(X = k) = \underbrace{(1-p)^{k-1}}_{\small k - 1\text{ failures}}\cdot \underbrace{p}_{\mathclap{\small \text{success}}}\)
    • Probability of \(k\) trials before first success

Less Common (But Important) Distributions

  • Discrete Uniform: \(N\) equally-likely outcomes
    • \(X \sim U\{{\color{purple}a},{\color{purple}b}\} \implies \mathcal{R}_X = \{a, a+1, \ldots, b\}, \Pr(X = k) = \frac{1}{{\color{purple}b} - {\color{purple}a} + 1}\)
  • Beta: \(X \sim \text{Beta}({\color{purple}\alpha}, {\color{purple}\beta})\): conjugate prior for Bernoulli, Binomial, and Geometric dists.
    • Intuition: If we use Beta to encode our prior hypothesis, then observe data drawn from Binomial, distribution of our updated hypothesis is still Beta.
    • \(\underbrace{\Pr(\text{biased}) = \Pr(\text{unbiased})}_{\text{Prior: }\text{Beta}({\color{purple}\alpha}, {\color{purple}\beta})} \rightarrow\) Observe \(\underbrace{\frac{8}{10}\text{ heads}}_{\text{Data}} \rightarrow \underbrace{\Pr(\text{biased}) = 0.65}_{\text{Posterior: }\text{Beta}({\color{purple}\alpha + 8}, {\color{purple}\beta + 2})}\)
  • Dirichlet: \(\mathbf{X} = (X_1, X_2, \ldots, X_K) \sim \text{Dir}({\color{purple} \boldsymbol\alpha})\)
    • \(K\)-dimensional extension of Beta (thus, conjugate prior for Multinomial)

Interactive Visualizations!

Seeing Theory, Brown University

Continuous Probability

  • (With some final reminders first!)

What Things Have Distributions?

  • Answer: Random Variables
  • Meaning: \(\mathcal{N}(0, 1)\) on its own is a “template”, an exhibit at a museum within a glass case
  • To start using it, e.g., to generate random values, we need to consider a particular RV \(X \sim \mathcal{N}(0,1)\), then generate values on basis of this template:
    • \(X = 0\) more likely than \(X = 1\) or \(X = -1\),
    • \(X = 1\) more likely than \(X = 2\) or \(X = -2\),
    • and so on

CDFs/pdfs/pmfs: What Are They?

  • Functions which answer questions about a Random Variable (\(X\) in this case) with respect to a non-random value (\(v\) in this case, for “value”)
  • CDF: What is probability that \(X\) takes on a value less than or equal to \(v\)?

\[ F_X(v) \definedas \Pr(X \leq v) \]

  • pmf: What is the probability of this exact value? (Discrete only)

\[ p_X(v) \definedas \Pr(X = v) \]

  • pdf: 🙈 …It’s the thing you integrate to get the CDF

\[ f_X(v) \definedas \frac{d}{dv}F_X(v) \iff \int_{-\infty}^{v} f_X(v)dv = F_X(v) \]

CDFs/pdfs/pmfs: Why Do We Use Them?

  • CDF is like the “API” that allows you to access all of the information about the distribution (pdf/pmf is derived from the CDF)
  • Example: we know there’s some “thing” called the Exponential Distribution…
  • How do we use this distribution to understand a random variable \(X \sim \text{Exp}(\lambda)\)?
    • Answer: the CDF of \(X\)!
    • Since all exponentially-distributed RVs have the same pdf (with different \(\lambda\) values plugged in), we can call this pdf “the” exponential distribution
  • Say we want to find the median of \(X\): The median is the number(s) \(m\) satisfying

\[ \Pr(X \leq m) = \frac{1}{2} \]

  • How can we find this? What “tool” do we use to figure this out about \(X\)?

Finding a Median via the CDF

Median of a Random Variable \(X\)

The median of a random variable \(X\) with some CDF \(F_X(v_X)\) is the [set of] numbers \(m\) for which the probability that \(X\) is lower than \(m\) is \(\frac{1}{2}\):

\[ \begin{align*} \text{Median}(X) &= \left\{m \left| F_X(m) = \frac{1}{2} \right. \right\} \\ &= \left\{m \left| \int_{-\infty}^{m}f_X(v_X)dv_X = \frac{1}{2} \right. \right\} \end{align*} \]

Median via CDF Example

Example: If \(X \sim \text{Exp}(\param{\lambda})\),

\[ F_X(v) = 1 - e^{-\lambda v} \]

So we want to solve for \(m\) in

\[ F_X(m) = \frac{1}{2} \iff 1 - e^{-\lambda m} = \frac{1}{2} \]

Step-by-Step

\[ \begin{align*} 1 - e^{-\lambda m} &= \frac{1}{2} \\ \iff e^{-\lambda m} &= \frac{1}{2} \\ \iff \ln\left[e^{-\lambda m}\right] &= \ln\left[\frac{1}{2}\right] \\ \iff -\lambda m &= -\ln(2) \\ \iff m &= \frac{\ln(2)}{\lambda} %3x = 19-2y \; \llap{\mathrel{\boxed{\phantom{m = \frac{\ln(2)}{\lambda}}}}}. \end{align*} \]

Top Secret Fun Fact

Every Discrete Distribution is [technically, in a weird way] a Continuous Distribution!

  • Same intuition as: every natural number is a real number, but converse not true

  • Marbles: Let \(X\) be a RV defined s.t. \(X(A) = 1\), \(X(B) = 2\), \(X(C) = 3\), \(X(D) = 4\). Then pmf for \(X\) is \(p_X(i) = \frac{1}{4}\) for \(i \in \{1, 2, 3, 4\}\).

  • We can then use the Dirac delta function \(\delta(v)\) to define a continuous pdf

    \[ f_X(v) = \sum_{i \in \mathcal{R}_X}p_X(i)\delta(v - i) = \sum_{i=1}^4p_X(i)\delta(v-i) = \frac{1}{4}\sum_{i=1}^4 \delta(v - i) \]

    and use either the (discrete) pmf \(p_X(v)\) or (continuous) pdf \(f_X(v)\) to describe \(X\):

\[ \begin{align*} \overbrace{\Pr(X \leq 3)}^{\text{CDF}} &= \sum_{i=1}^3\overbrace{p_X(i)}^{\text{pmf}} = \frac{1}{4} + \frac{1}{4} + \frac{1}{4} = \frac{3}{4} \\ \underbrace{\Pr(X \leq 3)}_{\text{CDF}} &= \int_{-\infty}^{3} \underbrace{f_X(v)}_{\text{pdf}} = \frac{1}{4}\int_{-\infty}^{3} \sum_{i = 1}^{4}\overbrace{\delta(v-i)}^{\small 0\text{ unless }v = i}dv = \frac{3}{4} \end{align*} \]

Common Continuous Distributions

  • Normal: The friend who shows up everywhere
  • Uniform: The stable, reliable friend
  • Exponential: Good days and bad days
  • Cauchy: Toxic af, stay away ☠️

[Recall] Binomial Distribution

Code 
k <- seq(0, 10)
prob <- dbinom(k, 10, 0.5)
bar_data <- tibble(k, prob)
ggplot(bar_data, aes(x=k, y=prob)) +
  geom_bar(stat="identity", fill=cbPalette[1]) +
  labs(
    title="Binomial Distribution, N = 10, p = 0.5",
    y="Probability Mass"
  ) +
  scale_x_continuous(breaks=seq(0,10)) +
  dsan_theme("half")

The Emergence of Order

  • Who can guess the state of this process after 10 steps, with 1 person?
  • 10 people? 50? 100? (If they find themselves on the same spot, they stand on each other’s heads)
  • 100 steps? 1000?

The Result: 16 Steps

The Result: 64 Steps

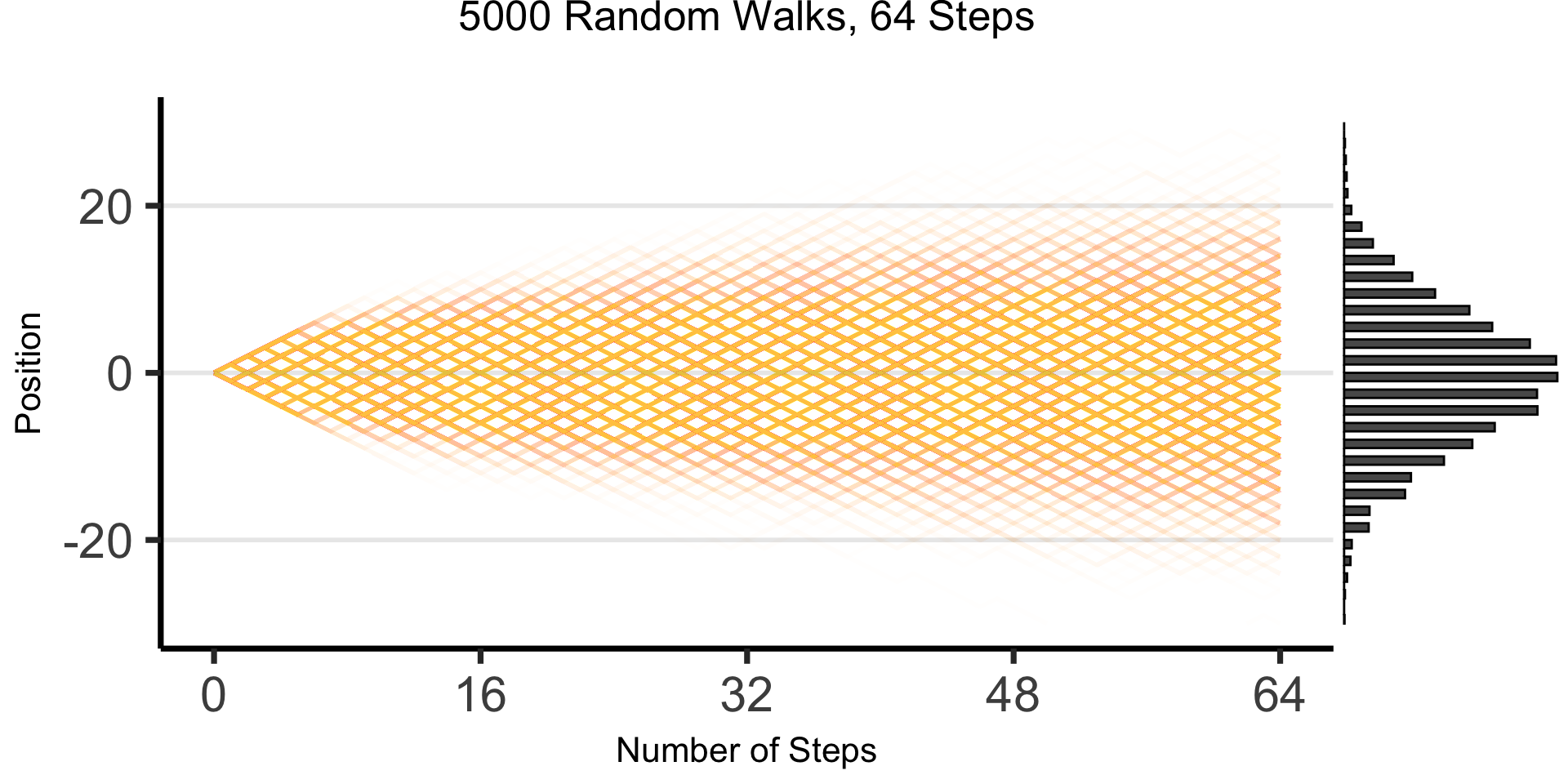
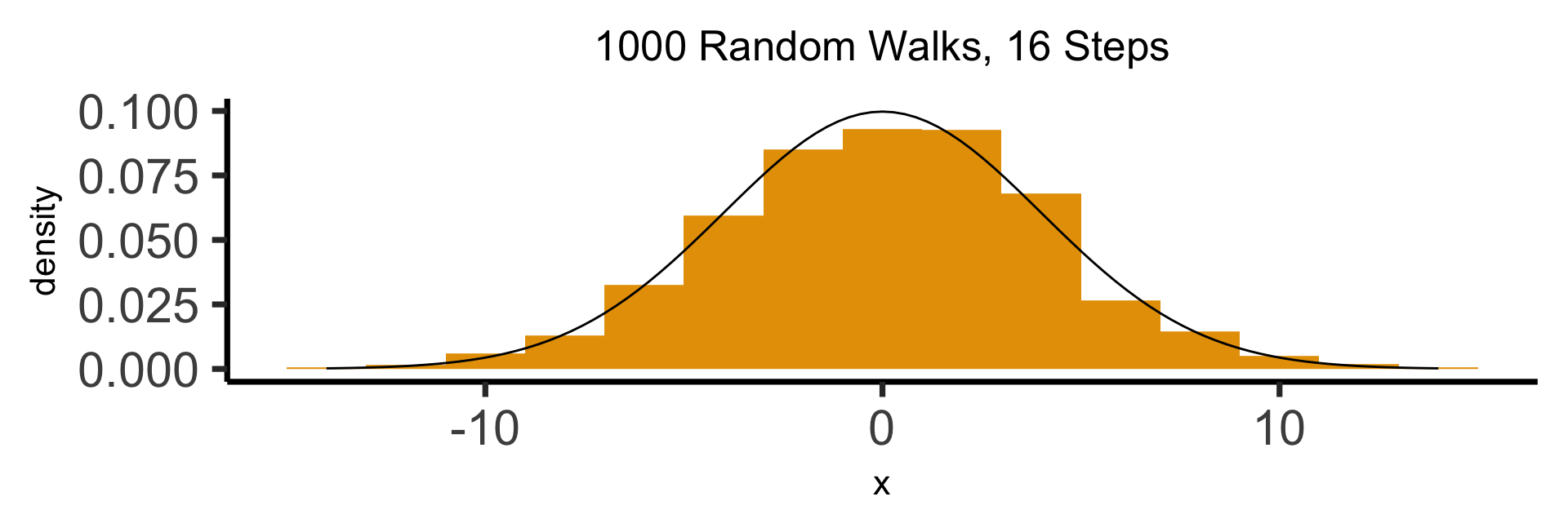
What’s Going On Here?

(Stay tuned for Markov processes \(\overset{t \rightarrow \infty}{\leadsto}\) Stationary distributions!)

Properties of the Normal Distribution

  • If \(X \sim \mathcal{N}(\param{\mu}, \param{\theta})\), then \(X\) has pdf \(f_X(v)\) defined by

\[ f_X(v) = \frac{1}{\sigma\sqrt{2\pi}}\bigexp{-\frac{1}{2}\left(\frac{v - \mu}{\sigma}\right)^2} \]

  • I hate memorizing as much as you do, I promise 🥴
  • The important part (imo): this is the most conservative out of all possible (symmetric) prior distributions defined on \(\mathbb{R}\) (defined from \(-\infty\) to \(\infty\))

“Most Conservative” How?

  • Of all possible distributions with mean \(\mu\), variance \(\sigma^2\), \(\mathcal{N}(\mu, \sigma^2)\) is the entropy-maximizing distribution
  • Roughly: using any other distribution (implicitly/secretly) imports additional information beyond the fact that mean is \(\mu\) and variance is \(\sigma^2\)
  • Example: let \(X\) be an RV. If we know mean is \(\mu\), variance is \(\sigma^2\), but then we learn that \(X \neq 3\), or \(X\) is even, or the 15th digit of \(X\) is 7, can update \(\mathcal{N}(\mu,\sigma^2)\) to derive a “better” distribution (incorporating this additional info)

The Takeaway

  • Given info we know, we can find a distribution that “encodes” only this info
  • More straightforward example: if we only know that the value is something in the range \([a,b]\), entropy-maximizing distribution is the Uniform Distribution
If We Know And We Know (Max-Entropy) Distribution Is…
\(\text{Mean}[X] = \mu\) \(\text{Var}[X] = \sigma^2\) \(X \sim \mathcal{N}(\mu, \sigma^2)\)
\(\text{Mean}[X] = \lambda\) \(X \geq 0\) \(X \sim \text{Exp}\left(\frac{1}{\lambda}\right)\)
\(X \geq a\) \(X \leq b\) \(X \sim \mathcal{U}[a,b]\)

[Recall] Discrete Uniform Distribution

Code 
library(tibble)
bar_data <- tribble(
  ~x, ~prob,
  1, 1/6,
  2, 1/6,
  3, 1/6,
  4, 1/6,
  5, 1/6,
  6, 1/6
)
ggplot(bar_data, aes(x=x, y=prob)) +
  geom_bar(stat="identity", fill=cbPalette[1]) +
  labs(
    title="Discrete Uniform pmf: a = 1, b = 6",
    y="Probability Mass",
    x="Value"
  ) +
  scale_x_continuous(breaks=seq(1,6)) +
  dsan_theme("half")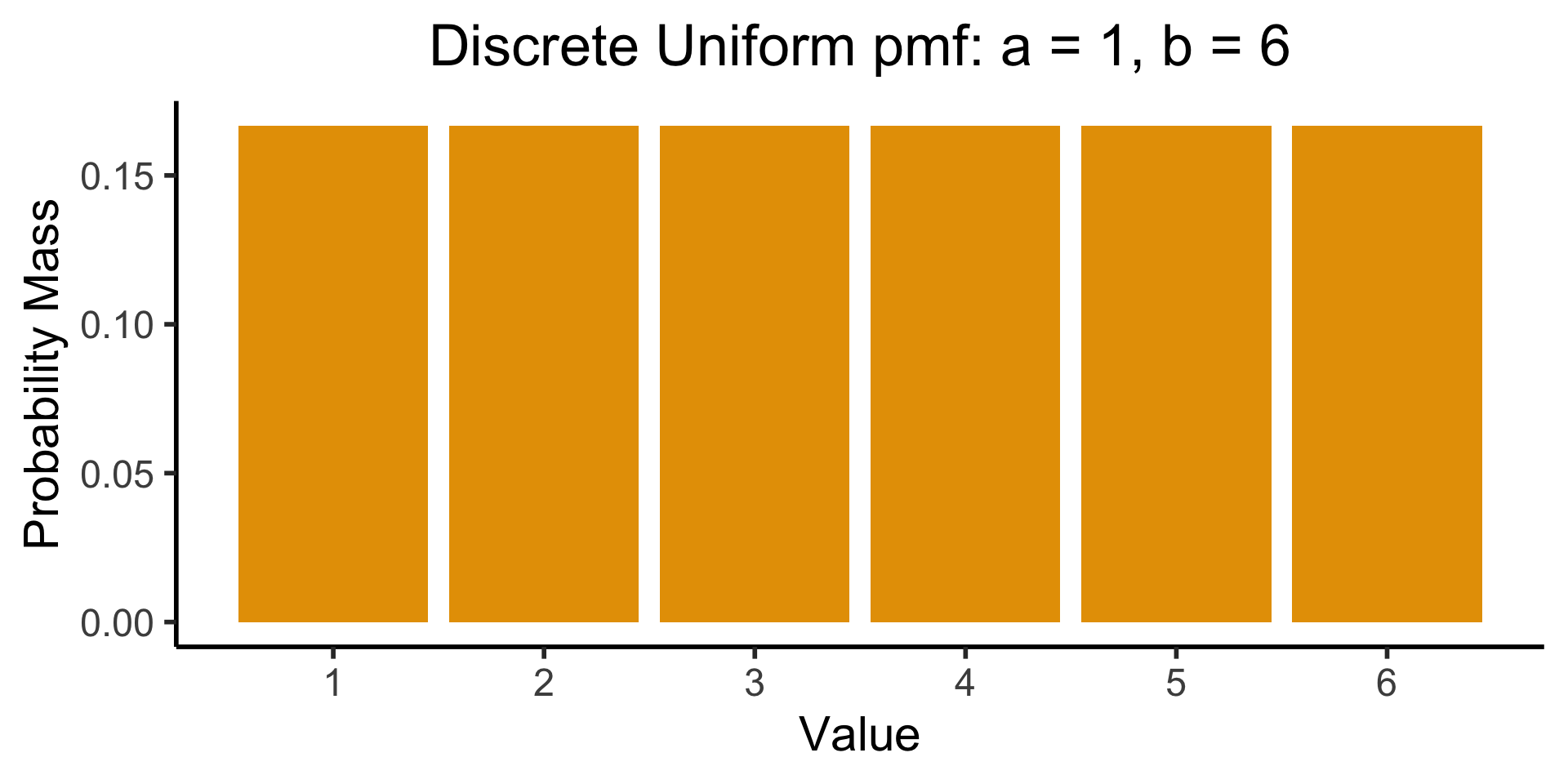

Continuous Uniform Distribution

  • If \(X \sim \mathcal{U}[a,b]\), then intuitively \(X\) is a value randomly selected from within \([a,b]\), with all values equally likely.
  • Discrete case: what we’ve been using all along (e.g., dice): if \(X \sim \mathcal{U}\{1,6\}\), then

\[ \Pr(X = 1) = \Pr(X = 2) = \cdots = \Pr(X = 6) = \frac{1}{6} \]

  • For continuous case… what do we put in the denominator? \(X \sim \mathcal{U}[1,6] \implies \Pr(X = \pi) = \frac{1}{?}\)…
    • Answer: \(\Pr(X = \pi) = \frac{1}{|[1,6]|} = \frac{1}{\aleph_0} = 0\)

Constructing the Uniform CDF

  • We were ready for this! We already knew \(\Pr(X = v) = 0\) for continuous \(X\)
  • So, we forget about \(\Pr(X = v)\), and focus on \(\Pr(X \in [v_0, v_1])\).
  • In 2D (dartboard) we had \(\Pr(X \in \circ) = \frac{\text{Area}(\circ)}{\text{Area}(\Omega)}\), so here we should have

\[ P(X \in [v_0,v_1]) = \frac{\text{Length}([v_0,v_1])}{\text{Length}([1,6])} \]

  • And indeed, the CDF of \(X\) is \(\boxed{F_X(v) = \Pr(X \leq v) = \frac{v-a}{b-a}}\), so that

\[ \Pr(X \in [v_0,v_1]) = F_X(v_1) - F_X(v_0) = \frac{v_1-a}{b-a} - \frac{v_0-a}{b-a} = \frac{v_1 - v_0}{b-a} \]

  • Since \(a = 1\), \(b = 6\) in our example, \(\Pr(X \in [v_0,v_1]) = \frac{v_1-v_0}{6-1} = \frac{\text{Length}([v_0,v_1])}{\text{Length}([1,6])} \; ✅\)

Exponential Distribution

  • Recall the (discrete) Geometric Distribution:
Code 
library(ggplot2)
k <- seq(0, 8)
prob <- dgeom(k, 0.5)
bar_data <- tibble(k, prob)
ggplot(bar_data, aes(x = k, y = prob)) +
    geom_bar(stat = "identity", fill = cbPalette[1]) +
    labs(
        title = "Geometric Distribution pmf: p = 0.5",
        y = "Probability Mass"
    ) +
    scale_x_continuous(breaks = seq(0, 8)) +
    dsan_theme("half")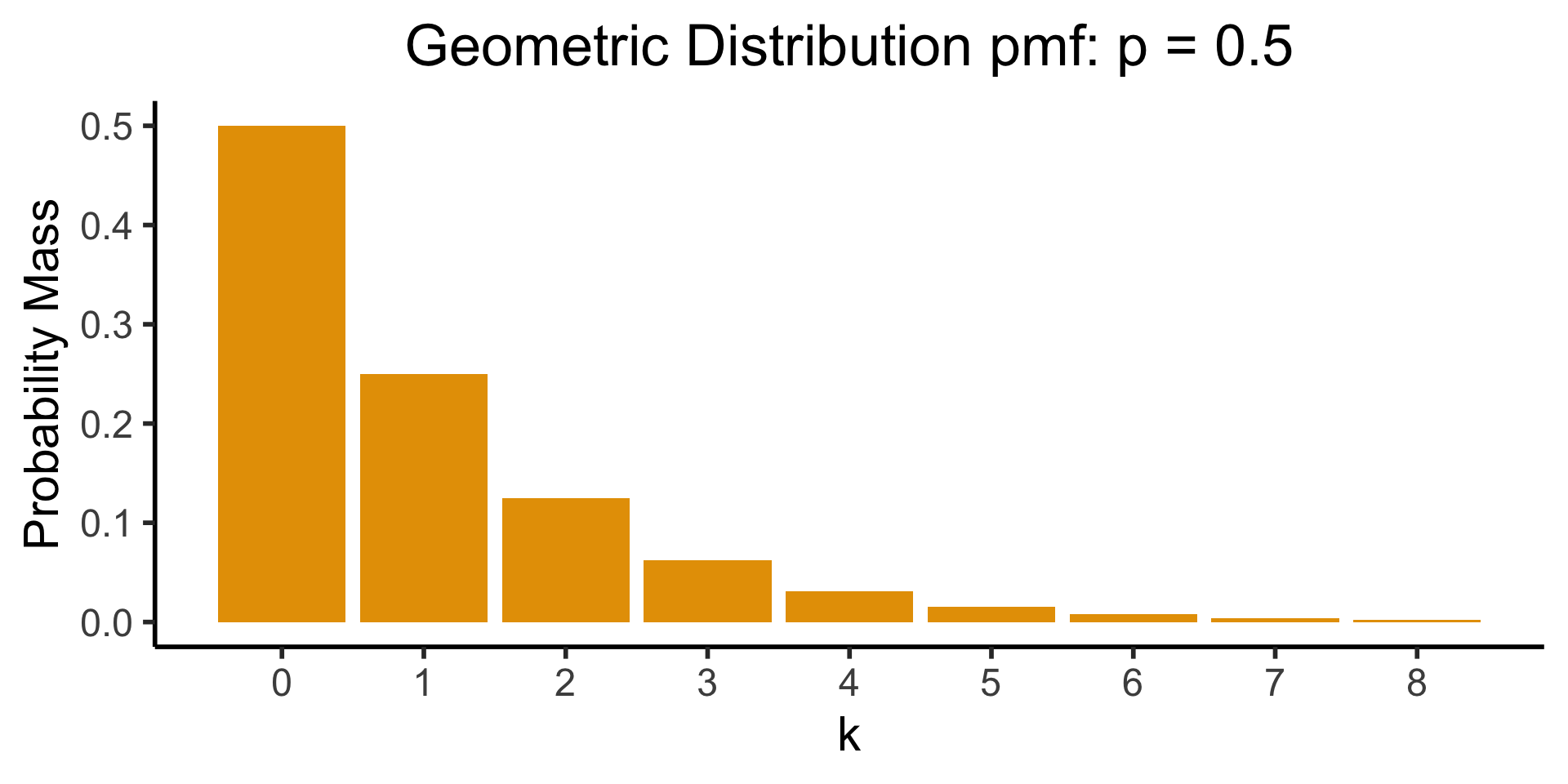

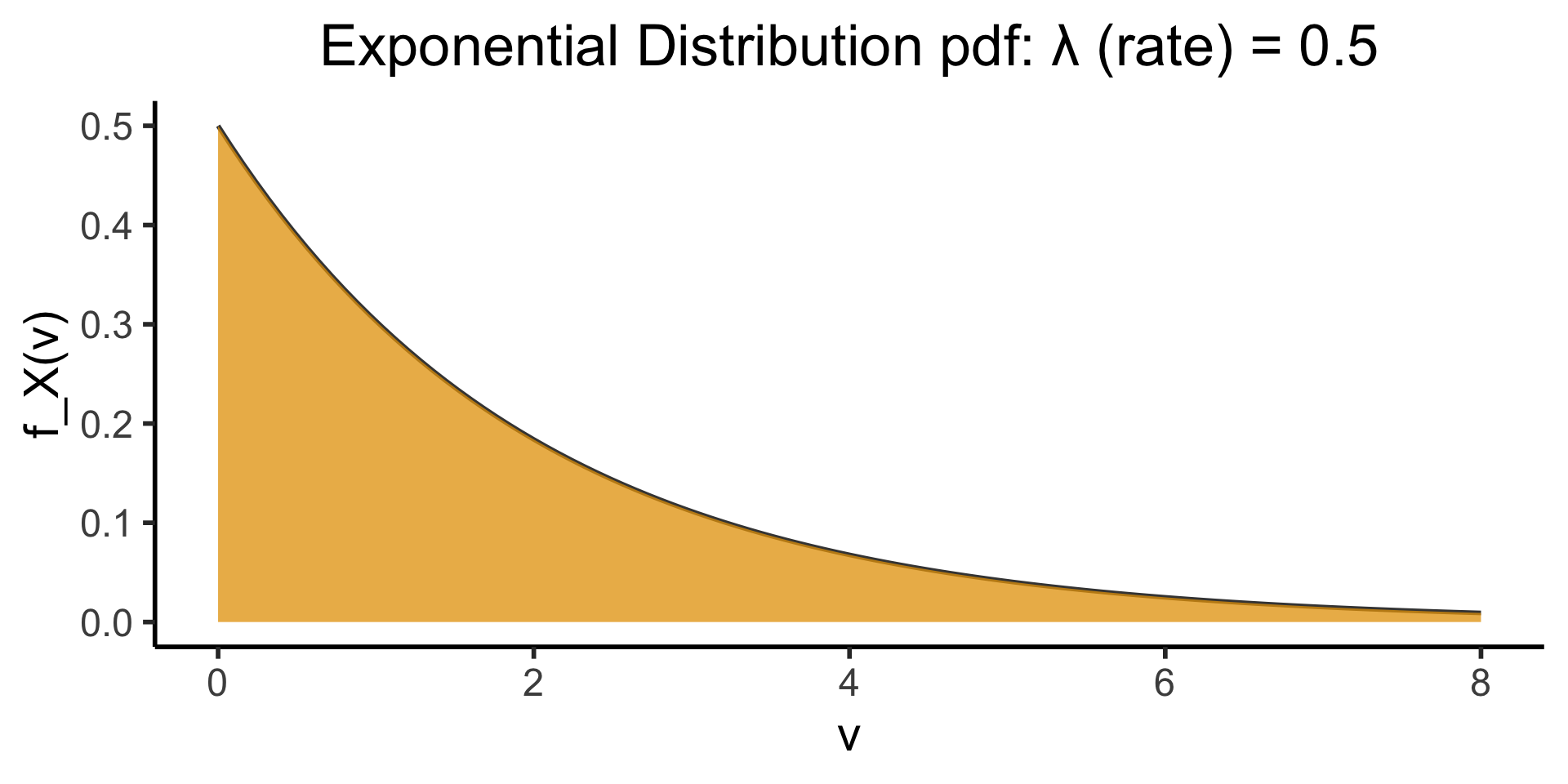
Now In Continuous Form!

Code 
my_dexp <- function(x) dexp(x, rate = 1/2)
ggplot(data.frame(x=c(0,8)), aes(x=x)) +
  stat_function(fun=my_dexp, size=g_linesize, fill=cbPalette[1], alpha=0.8) +
  stat_function(fun=my_dexp, geom='area', fill=cbPalette[1], alpha=0.75) +
  dsan_theme("half") +
  labs(
    title="Exponential Distribution pdf: λ (rate) = 0.5",
    x = "v",
    y = "f_X(v)"
  )

The Dreaded Cauchy Distribution

Code 
ggplot(data.frame(x=c(-4,4)), aes(x=x)) +
  stat_function(fun=dcauchy, size=g_linesize, fill=cbPalette[1], alpha=0.75) +
  stat_function(fun=dcauchy, geom='area', fill=cbPalette[1], alpha=0.75) +
  dsan_theme("quarter") +
  labs(
    title="PDF of R",
    x = "r",
    y = "f(r)"
  )
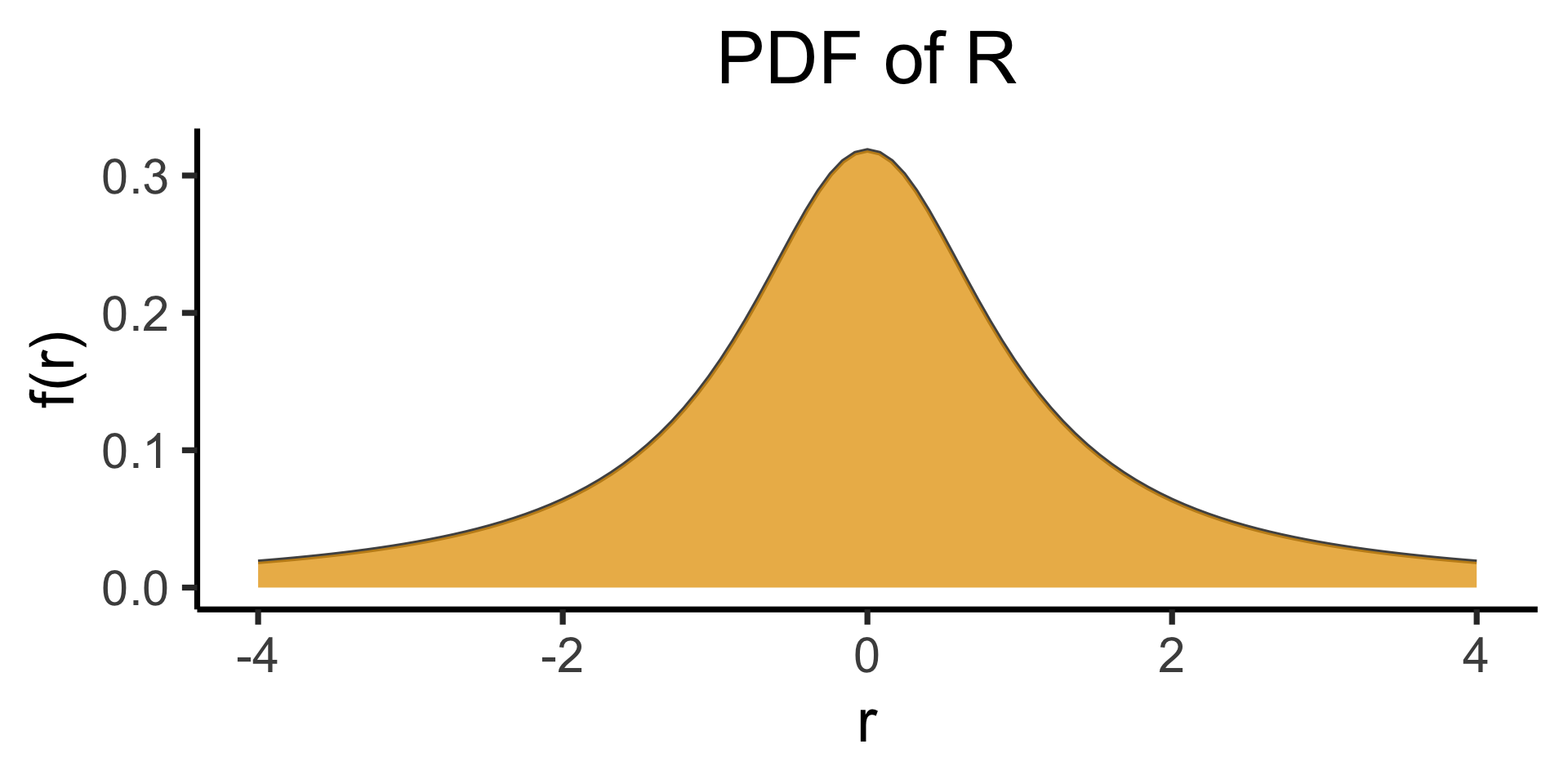
  • Paxton is a Houston Rockets fan, while Jeff is a Chicago Bulls fan. Paxton creates a RV \(H\) modeling how many games above .500 (wins minus losses) the Rockets will be in a season, while Jeff creates a similar RV \(C\) for the Bulls
  • They decide to combine their RVs to create a new RV, \(R = \frac{H}{C}\), which now models how much better the Nuggets will be in a season (\(R\) for “Ratio”)
  • For example, if the Rockets are \(10\) games above .500, while the Bulls are only \(5\) above .500, \(R = \frac{10}{5} = 2\). If they’re both 3 games above .500, \(R = \frac{3}{3} = 1\).

So What’s the Issue?

So far so good. It turns out (though Paxton and Jeff don’t know this) the teams are both mediocre: \(H \sim \mathcal{N}(0,10)\), \(B \sim \mathcal{N}(0,10)\)… What is the distribution of \(R\)?

\[ \begin{gather*} R \sim \text{Cauchy}\left( 0, 1 \right) \end{gather*} \]

\[ \begin{align*} \expect{R} &= ☠️ \\ \Var{R} &= ☠️ \\ M_R(t) &= ☠️ \end{align*} \]

From Agnesi (1801) [Internet Archive]

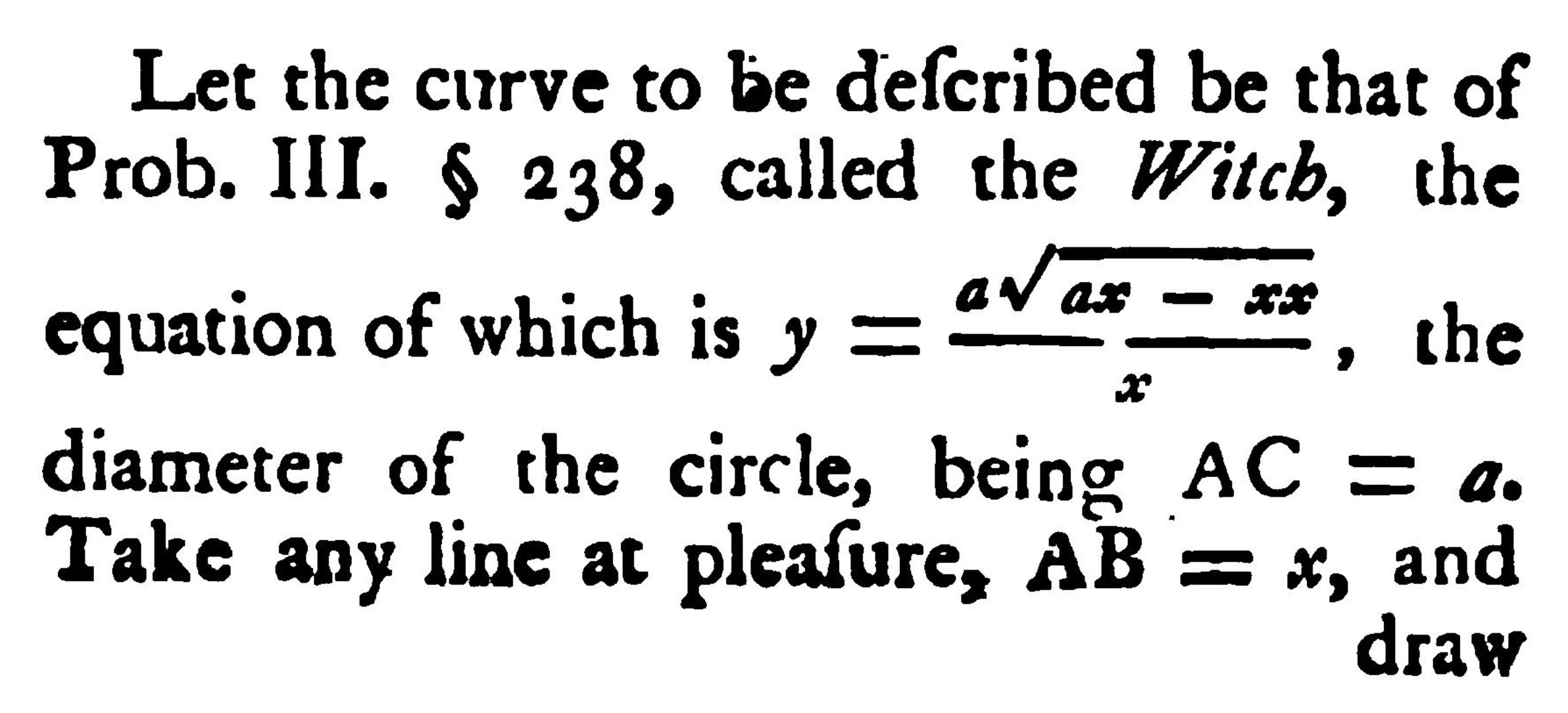
Even worse, this is true regardless of variances: \(D \sim \mathcal{N}(0,d)\) and \(W \sim \mathcal{N}(0,w)\) \(\implies R \sim \text{Cauchy}\left( 0,\frac{d}{w} \right)\)…

Lab 4

Lab 4 Demo

  • Lab 4 Demo Link
  • Choose your own adventure:
    • Official lab demo
    • Math puzzle lab demo
    • Move on to Expectation, Variance, Moments

Lab 4 Assignment Prep

One of my favorite math puzzles ever:

The Problem of the Broken Stick (Gardner 2001, 273–85)

If a stick is broken at random into three pieces, what is the probability that the pieces can be put back together into a triangle?

This cannot be answered without additional information about the exact method of breaking!

  • One method is to select, independently and at random, two points from the points that range uniformly along the stick, then break the stick at these two points
  • Suppose, however, that we interpret in a different way the statement “break a stick at random into three pieces”. We break the stick at random, we select randomly one of the two pieces, and we break that piece at random.
  • Will these two interpretations result in the same probabilities?
  • If yes, what is that probability?
  • If no, what are the probabilities in each case?

Lab 4 Assignment

References

Agnesi, Maria Gaetana. 1801. Analytical Institutions in Four Books: Originally Written in Italian. Taylor and Wilks. https://archive.org/details/analyticalinstit00agnerich/page/n3/mode/2up.
Gardner, Martin. 2001. Colossal Book of Mathematics: Classic Puzzles Paradoxes And Problems. W. W. Norton & Company.

Appendix I: Dirac Delta Function

\[ \delta(v) = \begin{cases}\infty & v = 0 \\ 0 & v \neq 0\end{cases} \]

\[ \int_{-\infty}^{\infty}\delta(v)dv = \theta(v) = \begin{cases} 1 & v = 0 \\ 0 & v \neq 0\end{cases} \]

Appendix II: Countability of \(\mathbb{Q}\)

  • Bad definition: “\(\mathbb{N}\) is countable because no \(x \in \mathbb{N}\) between \(0\) and \(1\). \(\mathbb{R}\) is uncountable because infinitely-many \(x \in \mathbb{R}\) between \(0\) and \(1\).” (\(\Rightarrow \mathbb{Q}\) uncountable)
  • And yet, \(\mathbb{Q}\) is countable…

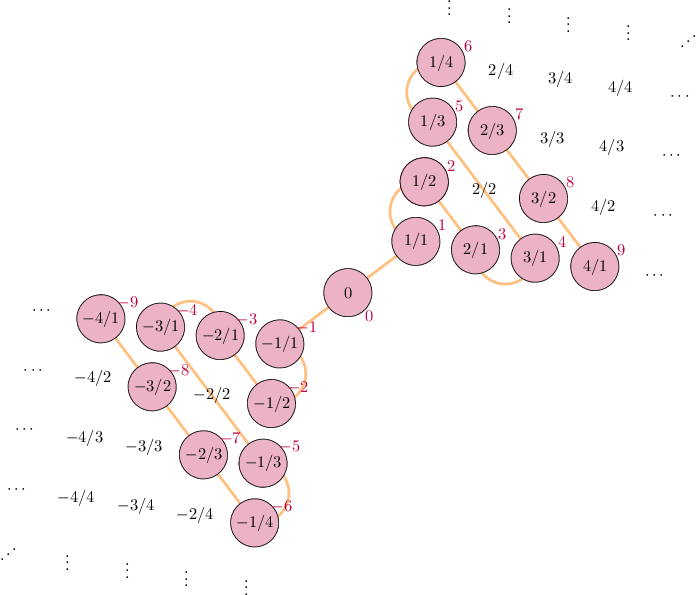
\[ \begin{align*} \begin{array}{ll} s: \mathbb{N} \leftrightarrow \mathbb{Z} & s(n) = (-1)^n \left\lfloor \frac{n+1}{2} \right\rfloor \\ h_+: \mathbb{Z}^+ \leftrightarrow \mathbb{Q}^+ & p_1^{a_1}p_2^{a_2}\cdots \mapsto p_1^{s(a_1)}p_2^{s(a_2)}\cdots \\ h: \mathbb{Z} \leftrightarrow \mathbb{Q} & h(n) = \begin{cases}h_+(n) &n > 0 \\ 0 & n = 0 \\ -h_+(-n) & n < 0\end{cases} \\ (h \circ s): \mathbb{N} \leftrightarrow \mathbb{Q} & ✅🤯 \end{array} \end{align*} \]

Appendix III: Binomial Triangle