Week 9: Dimensionality Reduction

DSAN 5000: Data Science and Analytics

Prof. Jeff and Prof. James

Thursday, October 31, 2024

\(K\)-Means Clustering

K-Means Clustering Algorithm

What we’re given:
  • Data \(\mathbf{X} = (X_1 = \mathbf{x}_1, \ldots, X_N = \mathbf{x}_N)\)
  • Distance metric \(d(\mathbf{v}_1, \mathbf{v}_2)\)
  • Hyperparameter value for \(K\) (⁉️)
Our goal:
  • Assign each point \(\mathbf{x}_i\) to a cluster \(C_i \in \{1, \ldots, K\}\) (so \(S_j = \{\mathbf{x}_i \mid C_i = j\}\) is the set of points assigned to cluster \(j\))

K-Means Clustering Algorithm

  1. Initialize \(K\) random centroids \(\boldsymbol\mu_1, \ldots, \boldsymbol\mu_K\)

  2. (Re-)Compute distance \(d(\mathbf{x}_i, \boldsymbol\mu_j)\) from each point \(\mathbf{x}_i\) to each centroid \(\boldsymbol\mu_j\)

  3. (Re-)Assign points to class of nearest centroid: \(C_i = \argmin_j d(\mathbf{x}_i, \boldsymbol\mu_j)\)

  4. (Re-)compute centroids as mean of points in each cluster:

    \[ \mu_j^\text{new} \leftarrow \frac{1}{|S_j|}\sum_{\mathbf{x}_i \in S_j}\mathbf{x}_i \]

  5. Repeat Steps 2-4 until convergence

K-Means Clustering: Centroids

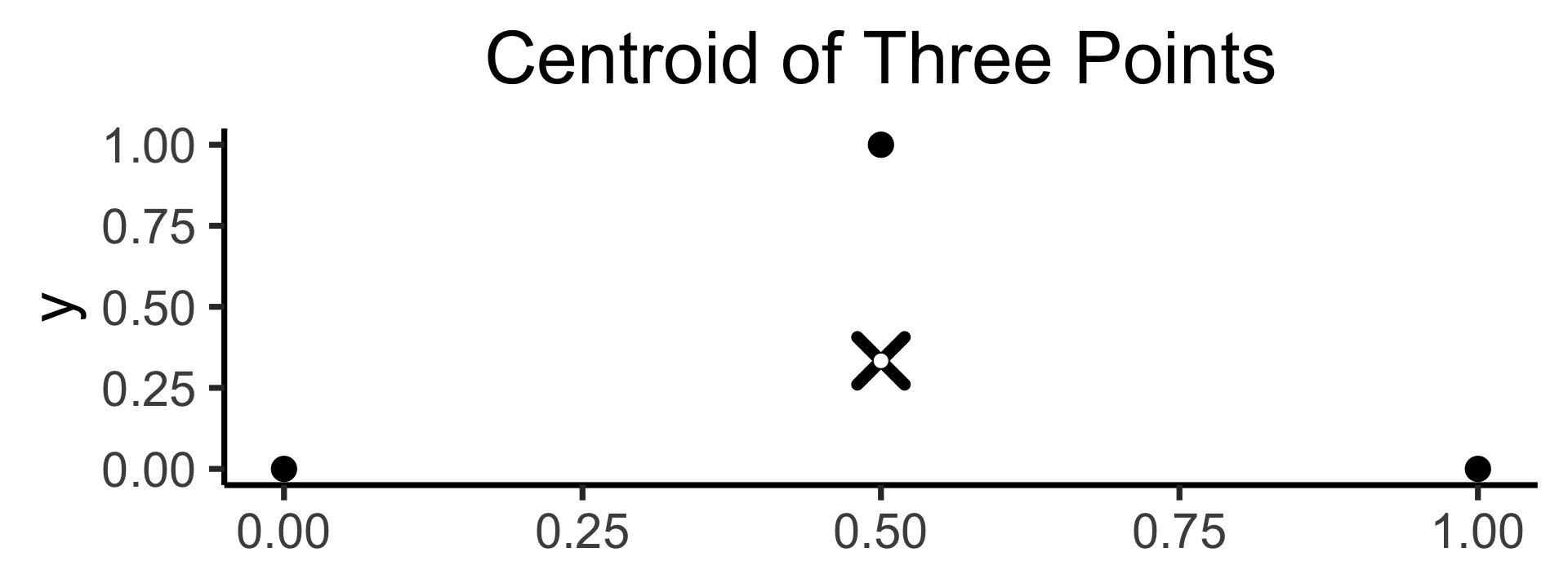
  • In general, the centroid \(\mu(S)\) of a set of \(N\) points \(S = \{\mathbf{x}_1, \mathbf{x}_2, \ldots, \mathbf{x}_n\}\) is just the arithmetic mean of all points in \(S\):

\[ \mu(S) = \frac{1}{|S|}\sum_{\mathbf{x}_i \in S}\mathbf{x}_i \]

Example 1: \(N = 3\) Points

\[ \begin{align*} \mathbf{x}_1 &= (\phantom{0}0\phantom{0}, 0) \\ \mathbf{x}_2 &= (\phantom{0}1\phantom{0}, 0) \\ \mathbf{x}_3 &= (0.5~, 1) \end{align*} \]

\[ \implies \]

\[ \mu(\mathbf{X}) = \left( \frac{1}{2}, \frac{1}{3} \right) \\ \]

Code 
library(tidyverse) |> suppressPackageStartupMessages()
simple_df <- tribble(
    ~x, ~y,
    0, 0,
    1, 0,
    0.5, 1
)
cent_x_simple <- mean(simple_df$x)
cent_y_simple <- mean(simple_df$y)
cent_df_simple <- tibble(x=cent_x_simple, y=cent_y_simple)
ggplot(simple_df, aes(x=x, y=y)) +
  geom_point(size = g_pointsize) +
  geom_point(
    data=cent_df_simple,
    aes(x=x, y=y),
    shape=4, stroke=4, color='black',
    size = g_pointsize * 1.5
  ) +
  geom_point(
    data=cent_df_simple,
    aes(x=x, y=y),
    shape=19, color='white',
    size = g_pointsize / 2) +
  dsan_theme('quarter') +
  labs(
    title = "Centroid of Three Points"
  ) +
  theme(
    axis.title.x = element_blank()
  )

Example 2: \(N = 250\) Points
Code 
N <- 250
r1_vals <- runif(N, 0, 1)
r2_vals <- runif(N, 0, 1)
triangle_df <- tibble(r1=r1_vals, r2=r2_vals)
v1 <- c(0,0)
v2 <- c(1,0)
v3 <- c(0,1)
triangle_df <- triangle_df |> mutate(
    bary_w1 = 1 - sqrt(r1),
    bary_w2 = sqrt(r1) * (1 - r2),
    bary_w3 = sqrt(r1) * r2
)
triangle_df <- triangle_df |> mutate(
    x = bary_w1 * v1[1] + bary_w2 * v2[1] + bary_w3 * v3[1],
    y = bary_w1 * v1[2] + bary_w2 * v2[2] + bary_w3 * v3[2]
)
triangle_cent_x <- mean(triangle_df$x)
triangle_cent_y <- mean(triangle_df$y)
triangle_cent_df <- tibble(x=triangle_cent_x, y=triangle_cent_y)
triangle_plot <- ggplot(
    triangle_df,
    aes(x=x, y=y)
  ) +
  geom_point(
    size = g_pointsize / 2,
    color=cbPalette[1]
  ) +
  geom_point(
    data=triangle_cent_df,
    aes(x=x, y=y),
    shape=4, stroke=4, color='black',
    size = g_pointsize * 1.5) +
  geom_point(
    data=triangle_cent_df,
    aes(x=x, y=y),
    shape=19, color='white',
    size = g_pointsize / 2) +
  dsan_theme('quarter')
# Now a rectangle
x_coords_rect <- runif(N, 0.5, 1)
y_coords_rect <- runif(N, 0.5, 1)
rect_df <- tibble(x=x_coords_rect, y=y_coords_rect)
cent_x_rect <- mean(x_coords_rect)
cent_y_rect <- mean(y_coords_rect)
cent_df_rect <- tibble(x=cent_x_rect, y=cent_y_rect)
rect_plot <- triangle_plot +
  geom_point(
    data=rect_df,
    aes(x=x, y=y),
    size = g_pointsize / 2,
    color=cbPalette[2]
  ) +
  geom_point(
    data=cent_df_rect,
    aes(x=x, y=y),
    shape=4, stroke=4, color='black',
    size = g_pointsize * 1.5) +
  geom_point(
    data=cent_df_rect,
    aes(x=x, y=y),
    shape=19, color='white',
    size = g_pointsize / 2) +
  dsan_theme('half') +
  theme(
    axis.title.x = element_blank()
  )
rect_plot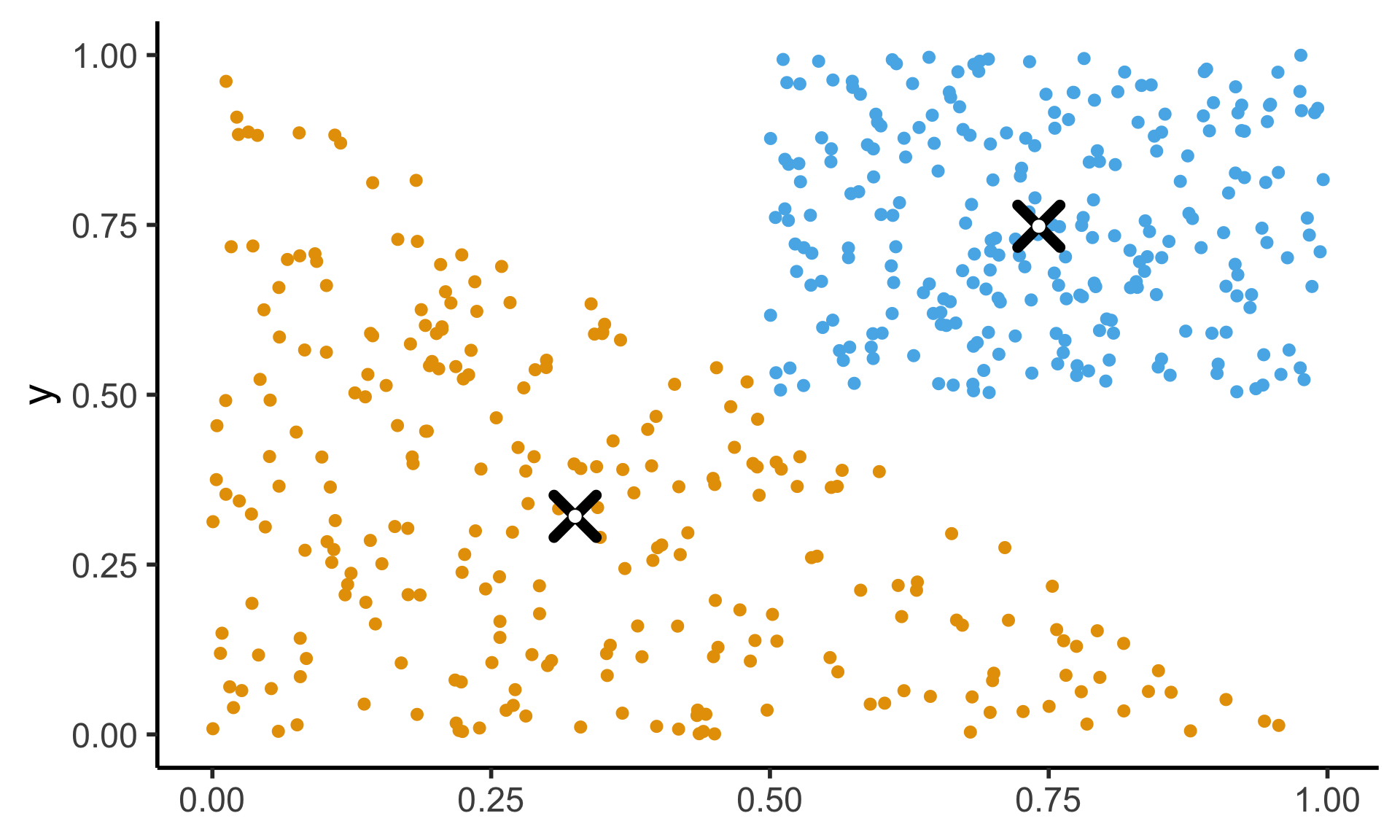

K-Means Clustering: Choosing K

  • Elbow Method
  • Gap Statistic
  • Silhouette

(Check out this incredibly helpful writeup covering each of these methods: it’s what I look at for reference whenever I’m trying to figure out a good value for \(K\) in my research!)

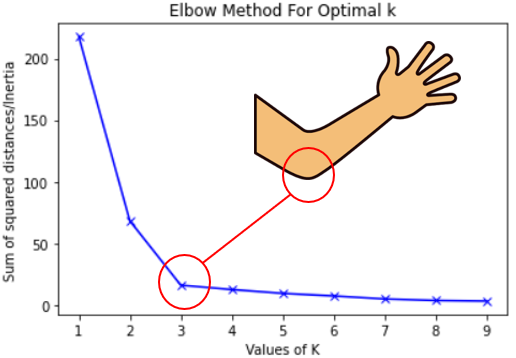
Elbow Method

  • Your lab involves generating an elbow plot!

Gap Statistic

  • From Tibshirani, Walther, and Hastie (2001)
  • Intuition: choice \(k\) is “good” for data \(\mathbf{X}\) if it produces clusters that are more cohesive than null distribution \(\mathbf{X}_0\) with points uniformly distributed in the same range as \(\mathbf{X}\):

\[ \text{Gap}_N(k) = \mathbb{E}_{\mathbf{X}_0}[\log(W_k)] - \log(W_k) \]

Code 
library(tidyverse)
library(patchwork)
library(MASS)
library(latex2exp)
N <- 300
x_coords_unif <- runif(N, 0, 1)
y_coords_unif <- runif(N, 0, 1)
unif_df <- tibble(x = x_coords_unif, y = y_coords_unif)
unif_df <- unif_df |> mutate(
    cluster = ifelse(y <= 0.5, 3, ifelse(x <= 0.5, 1, 2))
)
plot_title <- TeX(r"(Null Distribution $X_0$, k = 3)")
unif_gap_plot <- ggplot(unif_df, aes(x=x, y=y, color=factor(cluster))) +
  geom_point(size = g_pointsize / 2) +
  dsan_theme('half') +
  labs(
    title = plot_title,
    color = "Cluster"
  ) +
  coord_equal()
unif_gap_plot
N_cluster <- 100
sigma <- 0.01
Sigma <- matrix(c(sigma, 0, 0, sigma), nrow=2)
Mu1 <- c(0.2, 0.8)
Mu2 <- c(0.8, 0.8)
Mu3 <- c(0.5, 0.2)
cluster1 <- as_tibble(mvrnorm(N_cluster, Mu1, Sigma))
cluster1 <- cluster1 |> mutate(cluster = 1)
#print(cluster1)
cluster2 <- as_tibble(mvrnorm(N_cluster, Mu2, Sigma))
cluster2 <- cluster2 |> mutate(cluster = 2)
cluster3 <- as_tibble(mvrnorm(N_cluster, Mu3, Sigma))
cluster3 <- cluster3 |> mutate(cluster = 3)
cluster_df <- bind_rows(cluster1, cluster2, cluster3)
colnames(cluster_df) <- c("x","y","cluster")
cluster_gap_plot <- ggplot(cluster_df, aes(x=x, y=y, color=factor(cluster))) + 
  geom_point(size = g_pointsize / 2) +
  dsan_theme('half') +
  labs(
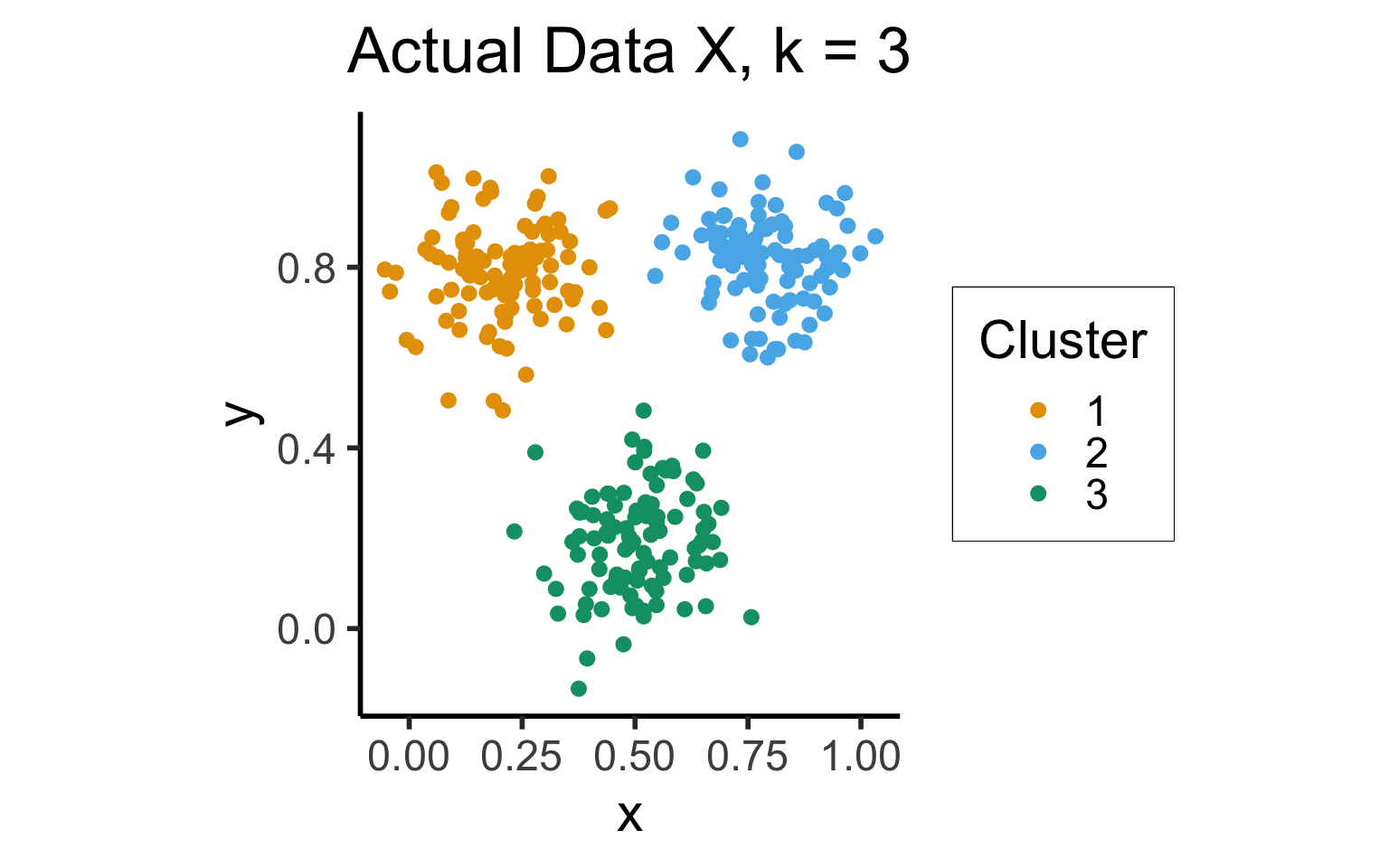
    title = "Actual Data X, k = 3",
    color = "Cluster"
  ) +
  coord_equal()
cluster_gap_plot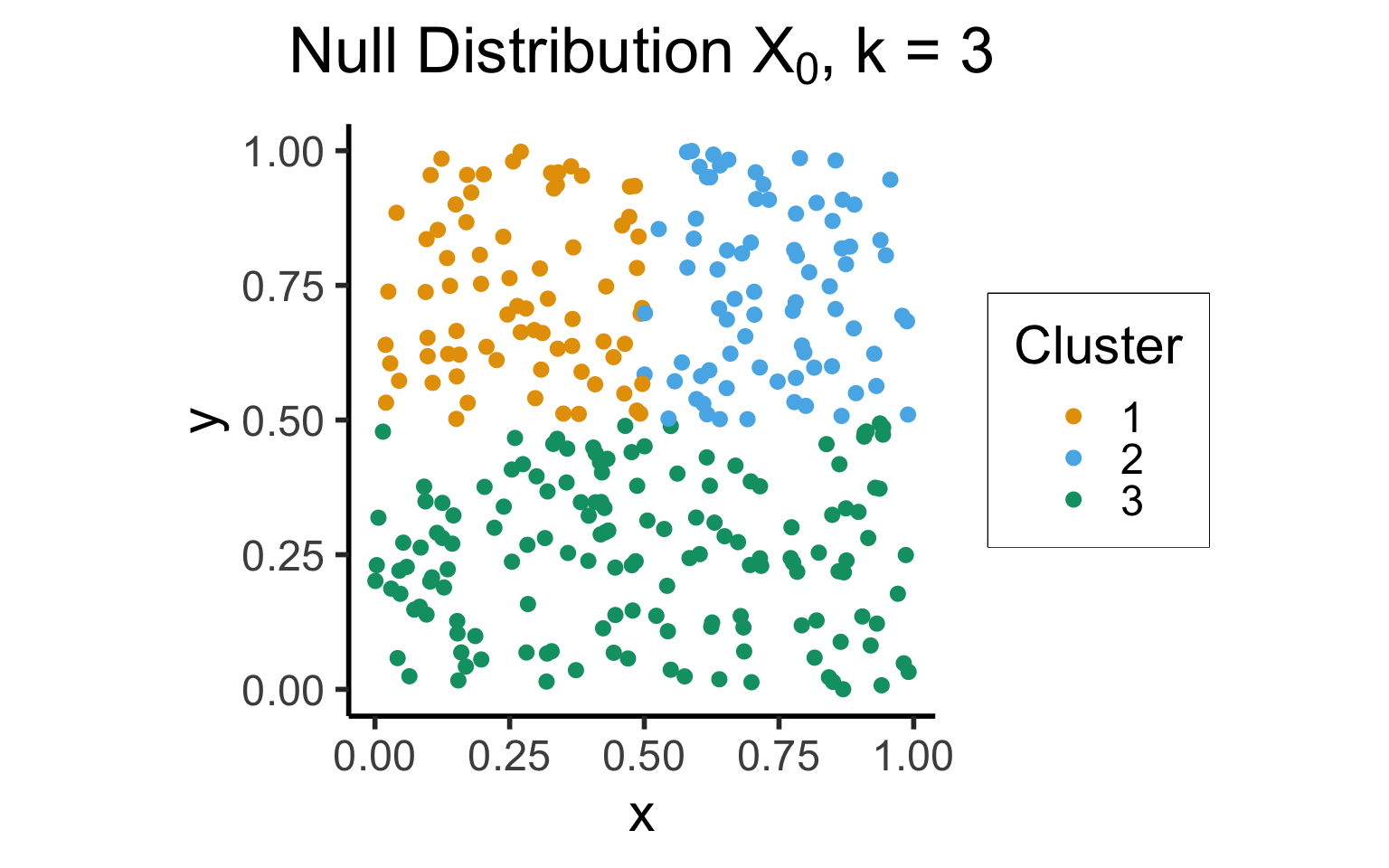

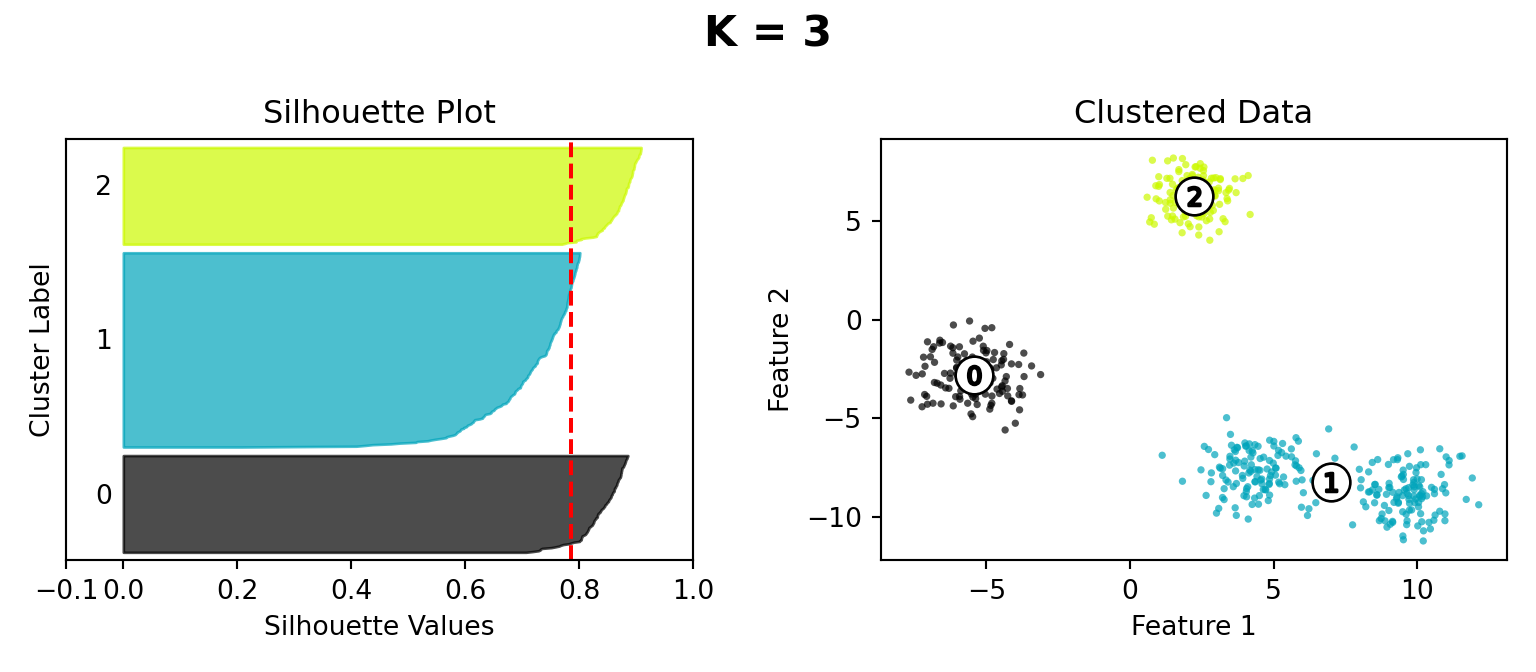
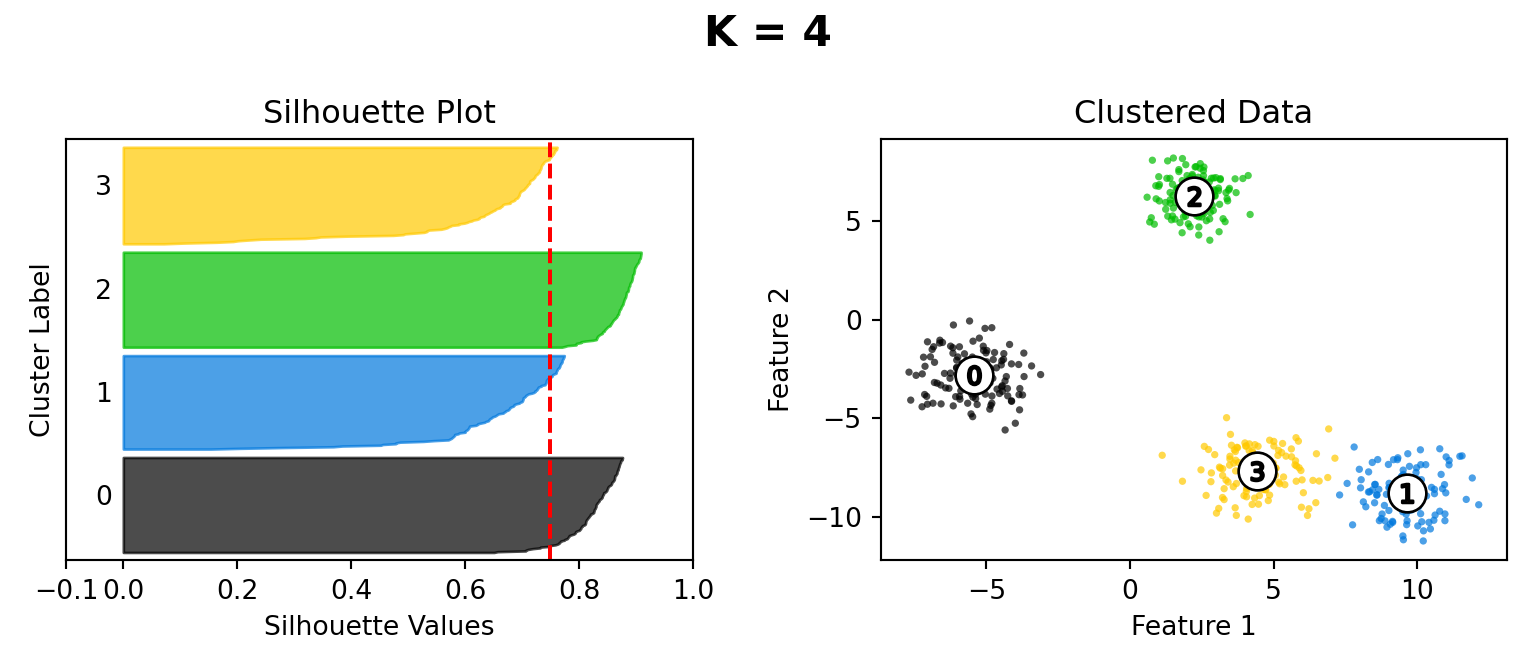
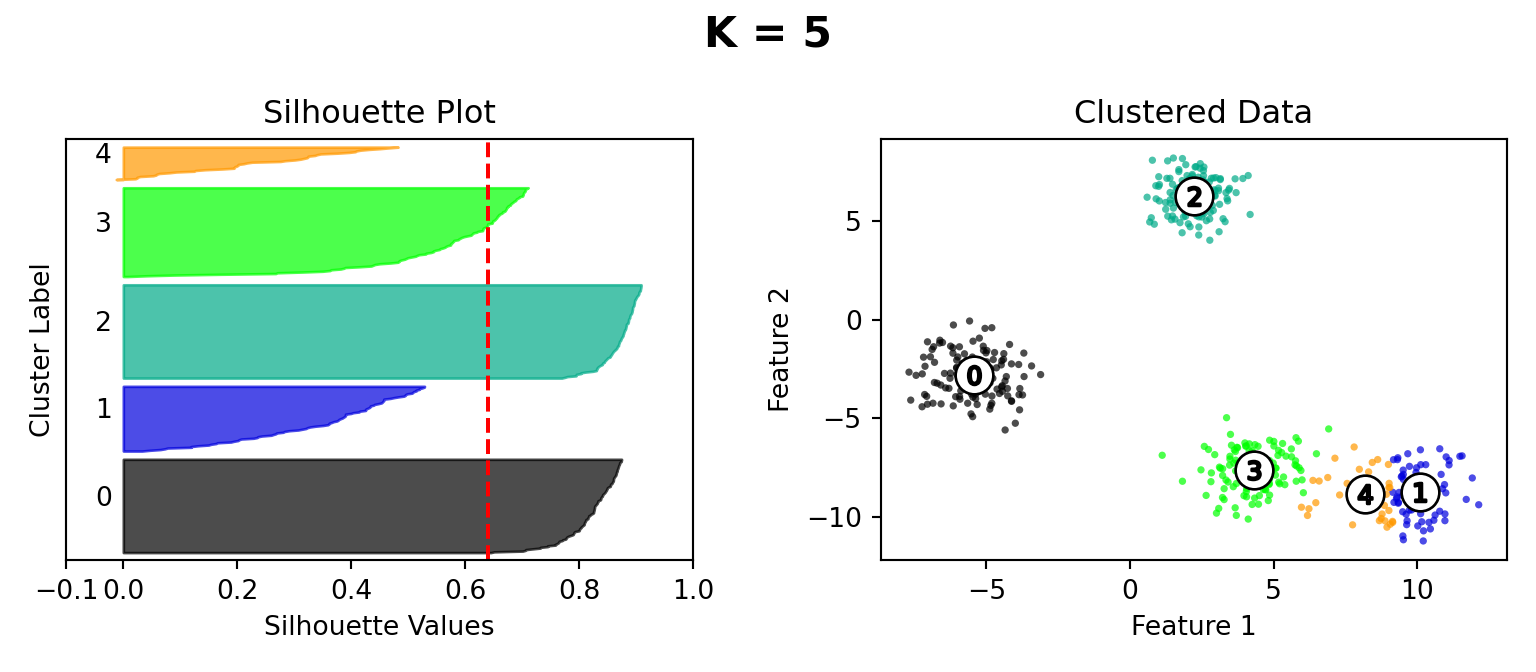
Silhouette Method

Code 
import matplotlib.cm as cm
import matplotlib.pyplot as plt
import numpy as np

from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
from sklearn.metrics import silhouette_samples, silhouette_score

# Generating the sample data from make_blobs
# This particular setting has one distinct cluster and 3 clusters placed close
# together.
X, y = make_blobs(
    n_samples=500,
    n_features=2,
    centers=4,
    cluster_std=1,
    center_box=(-10.0, 10.0),
    shuffle=True,
    random_state=5000
)

def silhouette_plot(n_clusters):
    # Create a subplot with 1 row and 2 columns
    fig, (ax1, ax2) = plt.subplots(1, 2)
    fig.set_size_inches(8, 3.5)

    # The 1st subplot is the silhouette plot
    # The silhouette coefficient can range from -1, 1 but in this example all
    # lie within [-0.1, 1]
    ax1.set_xlim([-0.1, 1])
    # The (n_clusters+1)*10 is for inserting blank space between silhouette
    # plots of individual clusters, to demarcate them clearly.
    ax1.set_ylim([0, len(X) + (n_clusters + 1) * 10])

    # Initialize the clusterer with n_clusters value and a random generator
    # seed of 10 for reproducibility.
    clusterer = KMeans(n_clusters=n_clusters, n_init="auto", random_state=10)
    cluster_labels = clusterer.fit_predict(X)

    # The silhouette_score gives the average value for all the samples.
    # This gives a perspective into the density and separation of the formed
    # clusters
    silhouette_avg = silhouette_score(X, cluster_labels)
    #print(
    #    "For n_clusters =",
    #    n_clusters,
    #    "The average silhouette_score is :",
    #    silhouette_avg,
    #)

    # Compute the silhouette scores for each sample
    sample_silhouette_values = silhouette_samples(X, cluster_labels)

    y_lower = 10
    for i in range(n_clusters):
        # Aggregate the silhouette scores for samples belonging to
        # cluster i, and sort them
        ith_cluster_silhouette_values = sample_silhouette_values[cluster_labels == i]

        ith_cluster_silhouette_values.sort()

        size_cluster_i = ith_cluster_silhouette_values.shape[0]
        y_upper = y_lower + size_cluster_i

        color = cm.nipy_spectral(float(i) / n_clusters)
        ax1.fill_betweenx(
            np.arange(y_lower, y_upper),
            0,
            ith_cluster_silhouette_values,
            facecolor=color,
            edgecolor=color,
            alpha=0.7,
        )

        # Label the silhouette plots with their cluster numbers at the middle
        ax1.text(-0.05, y_lower + 0.5 * size_cluster_i, str(i))

        # Compute the new y_lower for next plot
        y_lower = y_upper + 10  # 10 for the 0 samples

    ax1.set_title("Silhouette Plot")
    ax1.set_xlabel("Silhouette Values")
    ax1.set_ylabel("Cluster Label")

    # The vertical line for average silhouette score of all the values
    ax1.axvline(x=silhouette_avg, color="red", linestyle="--")

    ax1.set_yticks([])  # Clear the yaxis labels / ticks
    ax1.set_xticks([-0.1, 0, 0.2, 0.4, 0.6, 0.8, 1])

    # 2nd Plot showing the actual clusters formed
    colors = cm.nipy_spectral(cluster_labels.astype(float) / n_clusters)
    ax2.scatter(
        X[:, 0], X[:, 1], marker=".", s=30, lw=0, alpha=0.7, c=colors, edgecolor="k"
    )

    # Labeling the clusters
    centers = clusterer.cluster_centers_
    # Draw white circles at cluster centers
    ax2.scatter(
        centers[:, 0],
        centers[:, 1],
        marker="o",
        c="white",
        alpha=1,
        s=200,
        edgecolor="k",
    )

    for i, c in enumerate(centers):
        ax2.scatter(c[0], c[1], marker="$%d$" % i, alpha=1, s=50, edgecolor="k")

    ax2.set_title("Clustered Data")
    ax2.set_xlabel("Feature 1")
    ax2.set_ylabel("Feature 2")

    # plt.suptitle(
    #     "Silhouette analysis for KMeans clustering on sample data with n_clusters = %d"
    #     % n_clusters,
    #     fontsize=14,
    #     fontweight="bold",
    # )
    plt.suptitle("K = " + str(n_clusters), fontsize=16, fontweight="bold")
    plt.tight_layout()
    plt.show()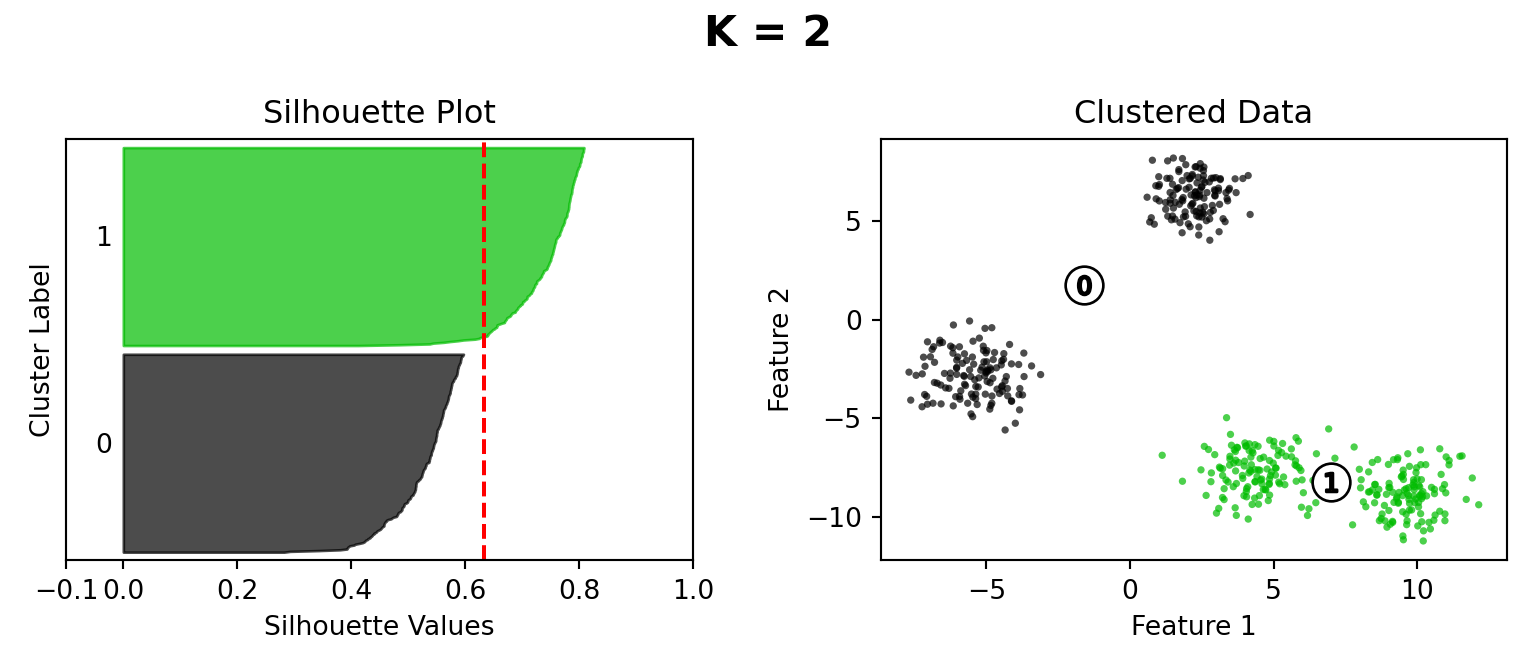

Dimensionality Reduction

Dimensionality Reduction: Why?

  • Dimensions are just numbers we use to describe where something is in some space
  • Do we really need 2 numbers to describe where we are on this line segment?
Code 
my_vec <- tribble(
    ~x, ~y, ~xend, ~yend,
    0, 0, 1, 1
)
my_dotted_vec <- tribble(
  ~x, ~y, ~xend, ~yend,
  1/3, 1, 1, 1/3
)
my_point <- tribble(
    ~x, ~y,
    2/3, 2/3,
)
my_line <- function(x) x
ggplot() +
  geom_segment(
    data=my_vec,
    aes(x=x, y=y, xend=xend, yend=yend),
    linewidth = g_linewidth,
    arrow = arrow(length = unit(0.1, "npc"))
  ) +
  geom_segment(
    data=my_dotted_vec,
    aes(x=x, y=y, xend=xend, yend=yend),
    linewidth = g_linewidth,
    linetype = "dashed"
  ) +
  geom_point(
    data=my_point,
    aes(x=x, y=y, color='jeff'),
    size = g_pointsize
  ) +
  #annotate("point", x = 2/3, y = 2/3, color = cbPalette[1], size = g_pointsize) +
#   geom_function(
#     data=data.frame(x=c(0,1)),
#     aes(x=x),
#     fun=my_line,
#     linewidth = g_linewidth
#   ) +
  annotate("text", x=1/3, y=1/3 + 0.05, label="2/3", angle=45, size=8, vjust='bottom') +
  annotate("text", x=4.8/6, y=4.8/6 + 0.05, label="1/3", angle=45, size=8, vjust='bottom') +
  dsan_theme('quarter') +
  labs(
    title = "Position of Your Boy Jeff w.r.t. v=(1,1)"
  ) +
  theme(
    title = element_text(size=18),
    legend.title = element_blank(),
    legend.spacing.y = unit(0, "mm")
  ) +
  #xlim(c(0,1)) + ylim(c(0,1)) +
  scale_color_manual(values=c('jeff'=cbPalette[1]), labels=c('jeff'="Your Boy Jeff")) +
  coord_equal()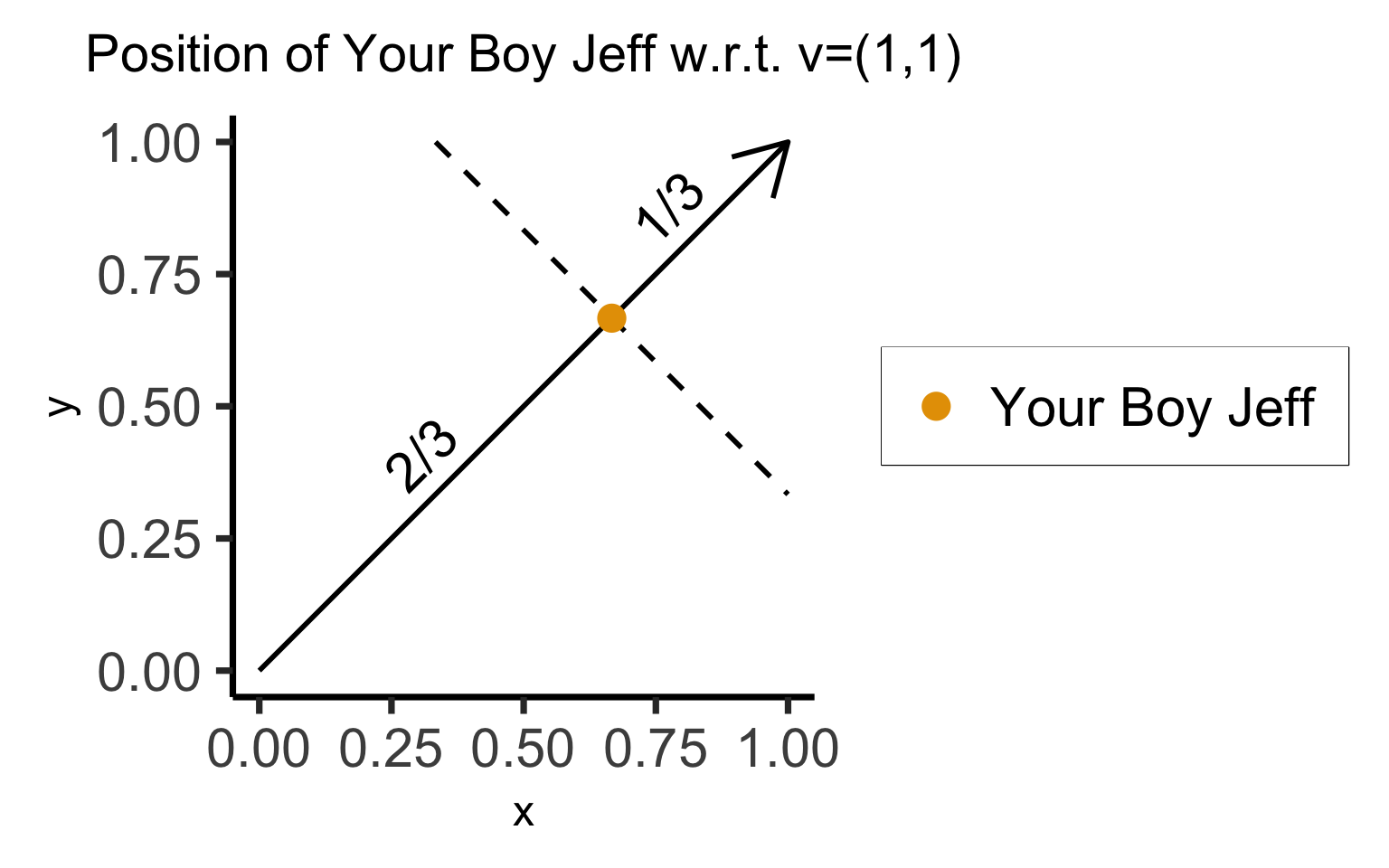

  • Representation 1: \(\text{Jeff} = \left(\frac{2}{3},\frac{2}{3}\right)\)
  • Representation 2: \(\text{Jeff} = \frac{2}{3} \cdot \mathbf{v}\)
  • If we have a 2D dataset (\(X_i \in \mathbb{R}^2\)), but we know that all points are in \(\text{Span}(\mathbf{v})\), we can obtain a 1-dimensional representation!

Dimensionality Reduction: Noisy Data

  • If points are perfectly linear, 1D representation perfectly compresses 2D data
  • Now, same intuition but with lossy representation: how many dimensions do we really need to describe where a person is on this line, to high approximation?
Code 
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
rng = np.random.default_rng(seed = 5000)
def set_seaborn_style():
    sns.set(rc={'figure.figsize':(4.5,4.5)})
    sns.set_theme(style="whitegrid")
set_seaborn_style()
N = 100
slope = 1
intercept = 0
# Now with noise
sigma = 0.1
x_coords = rng.uniform(0,1,N)
# Generate normally distributed random error ~ N(0, sigma**2)
errors = rng.normal(loc=0, scale=sigma, size=N)
y_coords = slope * x_coords + intercept + errors
random_line_df = pd.DataFrame({'x':x_coords, 'y':y_coords})
sns.scatterplot(data=random_line_df, x="x", y="y", color='black')
sns.rugplot(data=random_line_df, x="x", y="y", color='black')
plt.tight_layout()
plt.show()
from sklearn.decomposition import PCA
set_seaborn_style()
pca = PCA(n_components=2).fit(random_line_df.values)
Xp = pca.transform(random_line_df.values)
Xp_df = pd.DataFrame(Xp, columns=['x','y'])
pca_scatter = sns.scatterplot(data=Xp_df, x="x", y="y", color='black')
pca_scatter.set_xlim((-1,1));
pca_scatter.set_ylim((-1,1));
custom_ticks = [-1,-0.8,-0.6,-0.4,-0.2,0,0.2,0.4,0.6,0.8,1]
pca_scatter.set_xticks(custom_ticks)
pca_scatter.set_yticks(custom_ticks)
pca_scatter.set_xlabel("First Principal Component")
pca_scatter.set_ylabel("Second Principal Component")
plt.axhline(0, color='black', alpha=0.5)
plt.axvline(0, color='black', alpha=0.5)
sns.rugplot(data=Xp_df, x="x", y="y", color='black')
plt.tight_layout()
plt.show()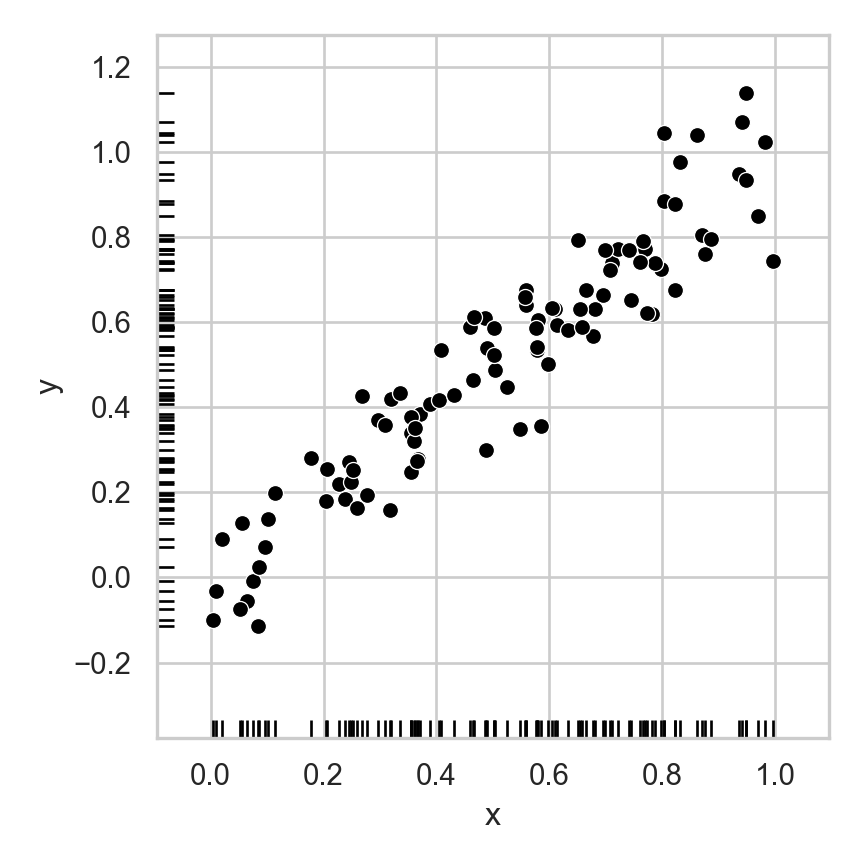

Sounds Good In Theory 🤔… How Does It Help Us Understand The Real World?

  • Represent politician \(i\) as a point \(\mathbf{v}_i = (v_{i,1}, v_{i,2}, \ldots, v_{i,N})\)
  • \(v_{i,j} \in \{Y, N\}\): politician \(i\)’s vote on bill \(j\)
  • Last US Congress (117th) voted on 1945 bills \(\implies\) 1945-dimensional space 😵‍💫
  • What happens if we view this 1945-dimensional space along two axes of maximum variance? (Same principle used to obtain principal component line on last slide)

Interactive version

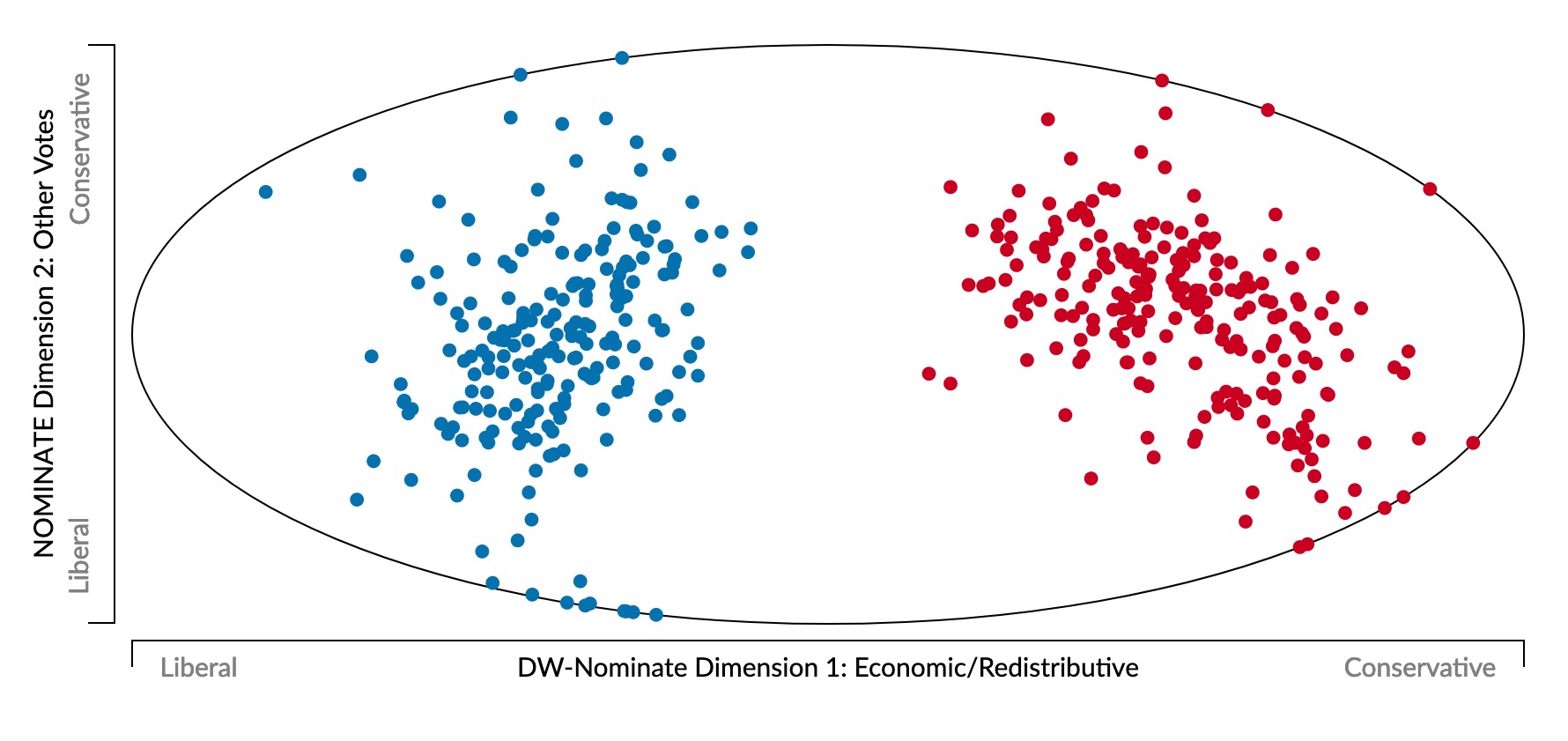
A Principled Quantification of Political Ideology 🤯

Code 
library(ggjoy)
metadata <- read_csv(
    "col_name      , col_width
     congress      , 4
     icpsr         , 6
     st_code       , 3
     cd            , 2
     st_name       , 8
     party_code    , 5
     mc_name       , 15
     dim_1         , 10
     dim_2         , 10
     dim_1_se      , 10
     dim_2_se      , 10
     dim_1_2_corr  , 8
     log_lik       , 11
     num_votes     , 5
     num_class_err , 5
     geo_mean_prob , 10"
)
members <- read_fwf(
    "assets/dwnom.DAT",
    fwf_widths(widths = metadata$col_width, col_names = metadata$col_name)
)
representatives <- members %>%
    filter(
        congress >= 88,
        !(cd %in% c(0, 98, 99)),
        party_code == 100 | party_code == 200
        ) %>%
    mutate(year1 = congress * 2 + 1787) %>%
    arrange(desc(year1))
democrats <- representatives %>% filter(party_code == 100)
republicans <- representatives %>% filter(party_code == 200)
ggplot(representatives, aes(x = dim_1, y = year1, group = year1)) +
    geom_joy(data = democrats, fill = "blue", scale = 7, size = 0.25, rel_min_height = 0.01, alpha = 0.2) +
    geom_joy(data = republicans, fill = "red", scale = 7, size = 0.25, rel_min_height = 0.01, alpha = 0.2) +
    theme_classic() +
    scale_x_continuous(limits = c(-1, 1.3), expand = c(0.01, 0), breaks = seq(-1, 1, 0.5)) +
    scale_y_reverse(breaks = seq(2013, 1963, -10)) +
    ggtitle("Distribution of DW-NOMINATE of U.S. House by Party: 1963-2013") +
    ylab("First Year of Each Congress") +
    xlab("First Dimension DW-NOMINATE") +
    dsan_theme('full')

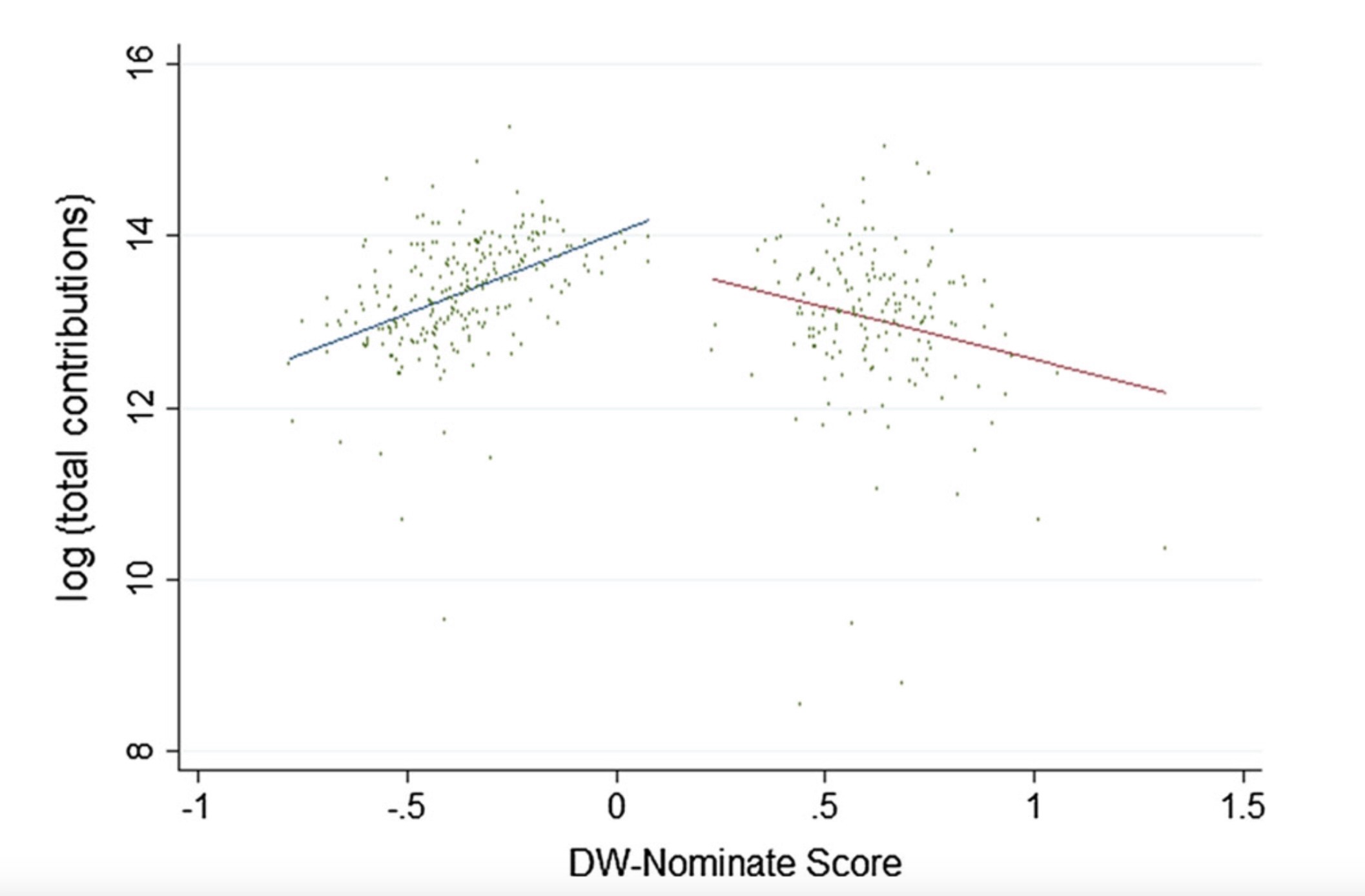
Political Contributions vs. Ideology

From Choi (2017)

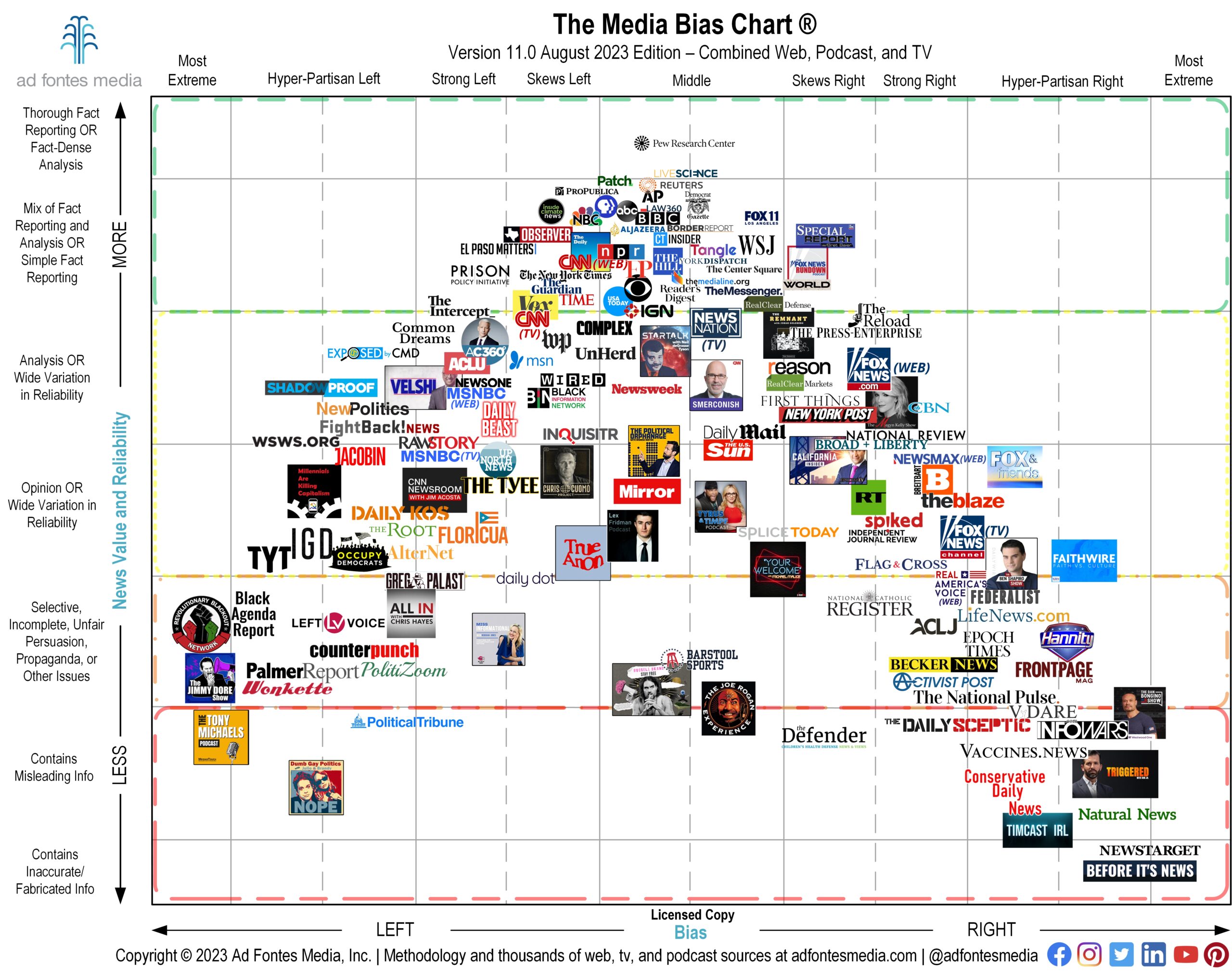
For Media Literacy

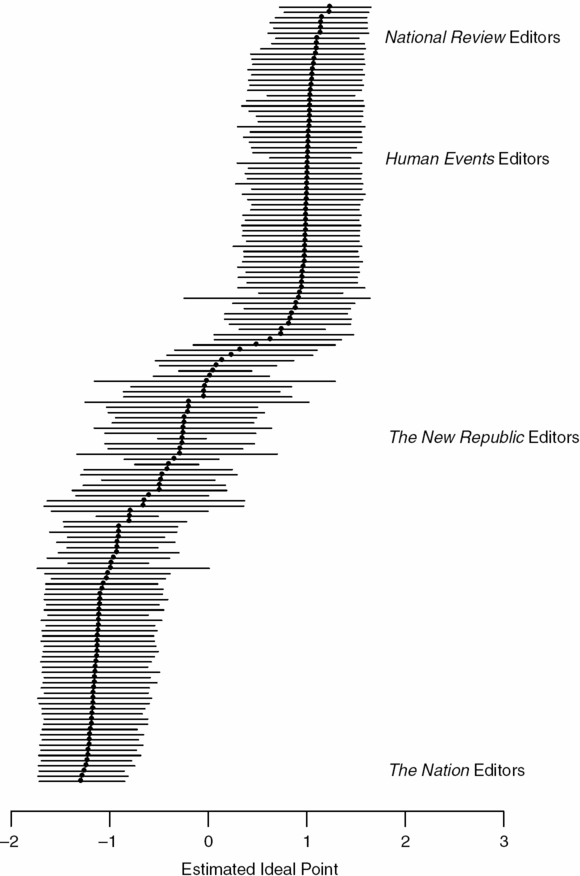
(A random person’s opinion; cited widely in Very Serious Discussions of politics)

(PCA scores painstakingly culled from millions of newspaper articles over many years; hidden on page 320 of Noel (2014))

For NLP

  • High-level goal: Retain information about word-context relationships while reducing the \(M\)-dimensional representations of each word down to 3 dimensions.
  • Low-level goal: Generate rank-\(K\) matrix \(\mathbf{W}\) which best approximates distances between words in \(M\)-dimensional space (rows in \(\mathbf{X}\))

But What Do The Vectors Mean?

  • The coordinates of a word vector \(\textbf{w}\) mean… the coordinates that best preserve its distance to other words in the high-dimensional space
  • However, you can transform the word vectors, or the space they’re plotted in, to impose meaning upon the otherwise-meaningless coordinates!

“Gaps” Between Vectors Also Meaningful!

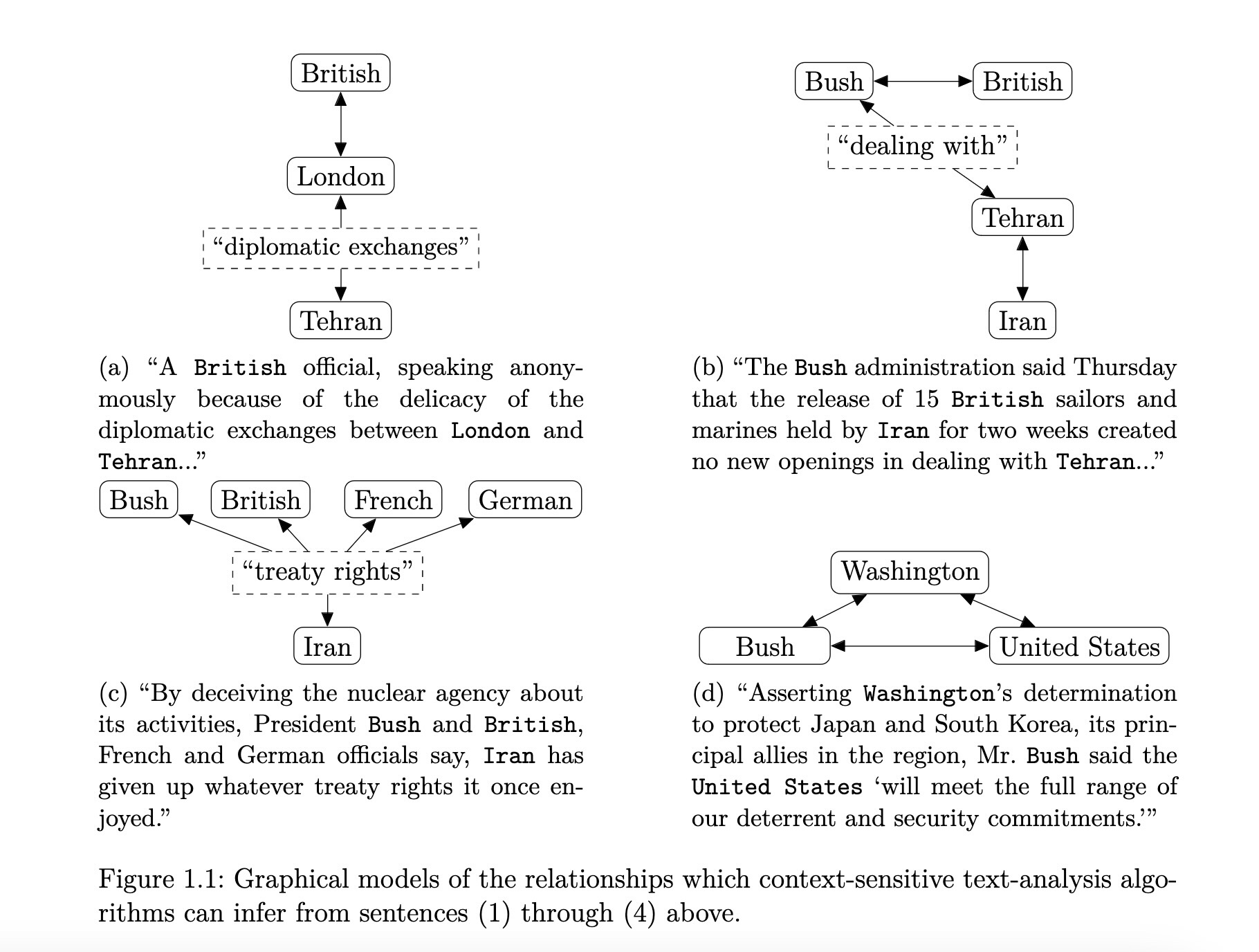
Coding Demo Interlude!

Clustering and Dimensionality Reduction for Text Data

Demo Link

Feature Extraction

Reducing Dimensionality

  • Method 1: Feature Selection. Selecting a subset of existing features:
\(F_1\) \(F_2\) \(F_3\)
0.8 0.9 0.1
0.6 0.4 0.1

→

\(F_1\) \(F_2\) \(F_3\)
0.8 0.9 0.1
0.6 0.4 0.1

→

\(F_1\) \(F_3\)
0.8 0.1
0.6 0.1
  • Method 2: Feature Extraction. Constructing new features as combinations/functions of the original features
\(F_1\) \(F_2\) \(F_3\)
0.8 0.9 0.1
0.6 0.4 0.1

→

\[ \begin{align*} {\color{#56b4e9}F'_{12}} &= \frac{{\color{#e69f00}F_1} + {\color{#e69f00}F_2}}{2} \\ {\color{#56b4e9}F'_{23}} &= \frac{{\color{#e69f00}F_2} + {\color{#e69f00}F_3}}{2} \end{align*} \]

→

\(F'_{12}\) \(F'_{23}\)
0.85 0.50
0.50 0.25

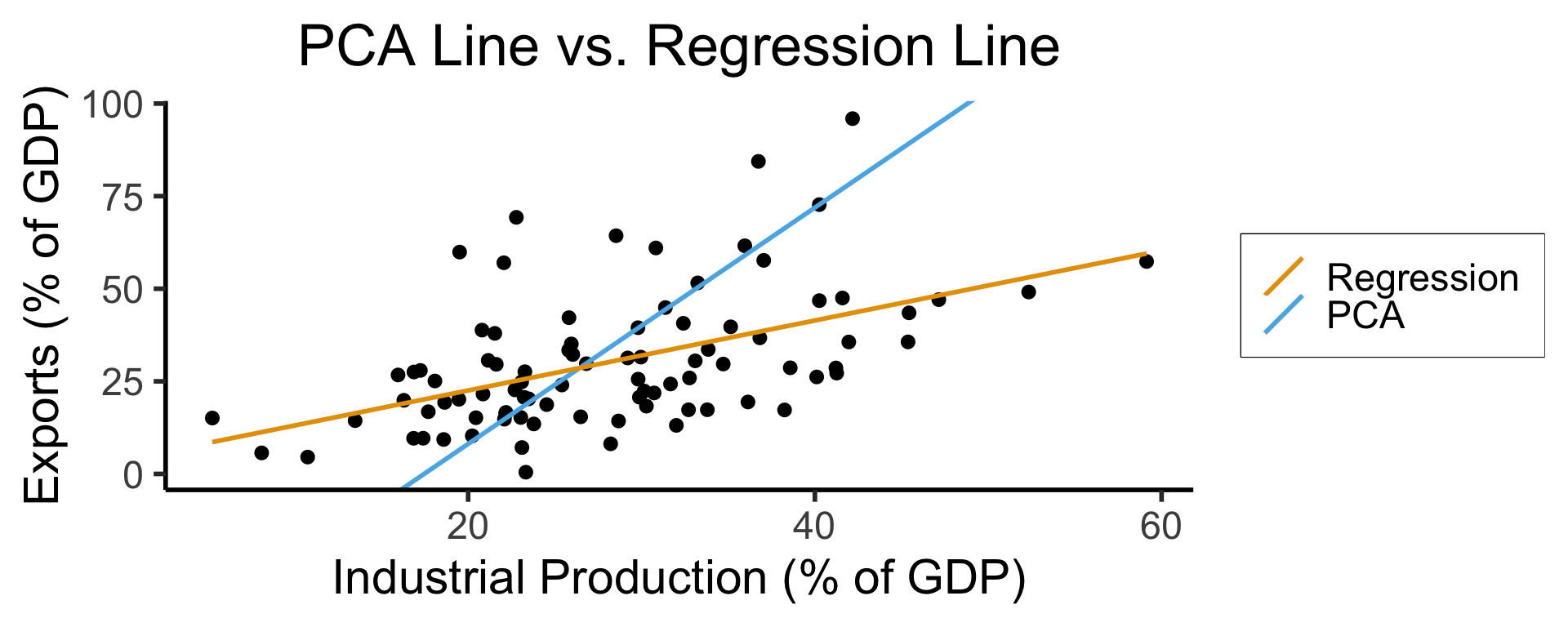
Principal Component Analysis (PCA)

  • We know this is feature extraction since we obtain new dimensions:
Code 
library(tidyverse) |> suppressPackageStartupMessages()
gdp_df <- read_csv("assets/gdp_pca.csv")

dist_to_line <- function(x0, y0, a, c) {
    numer <- abs(a * x0 - y0 + c)
    denom <- sqrt(a * a + 1)
    return(numer / denom)
}
# Finding PCA line for industrial vs. exports
x <- gdp_df$industrial
y <- gdp_df$exports
lossFn <- function(lineParams, x0, y0) {
    a <- lineParams[1]
    c <- lineParams[2]
    return(sum(dist_to_line(x0, y0, a, c)))
}
o <- optim(c(0, 0), lossFn, x0 = x, y0 = y)
ggplot(gdp_df, aes(x = industrial, y = exports)) +
    geom_point(size=g_pointsize/2) +
    geom_abline(aes(slope = o$par[1], intercept = o$par[2], color="pca"), linewidth=g_linewidth, show.legend = TRUE) +
    geom_smooth(aes(color="lm"), method = "lm", se = FALSE, linewidth=g_linewidth, key_glyph = "blank") +
    scale_color_manual(element_blank(), values=c("pca"=cbPalette[2],"lm"=cbPalette[1]), labels=c("Regression","PCA")) +
    dsan_theme("half") +
    remove_legend_title() +
    labs(
      title = "PCA Line vs. Regression Line",
        x = "Industrial Production (% of GDP)",
        y = "Exports (% of GDP)"
    )
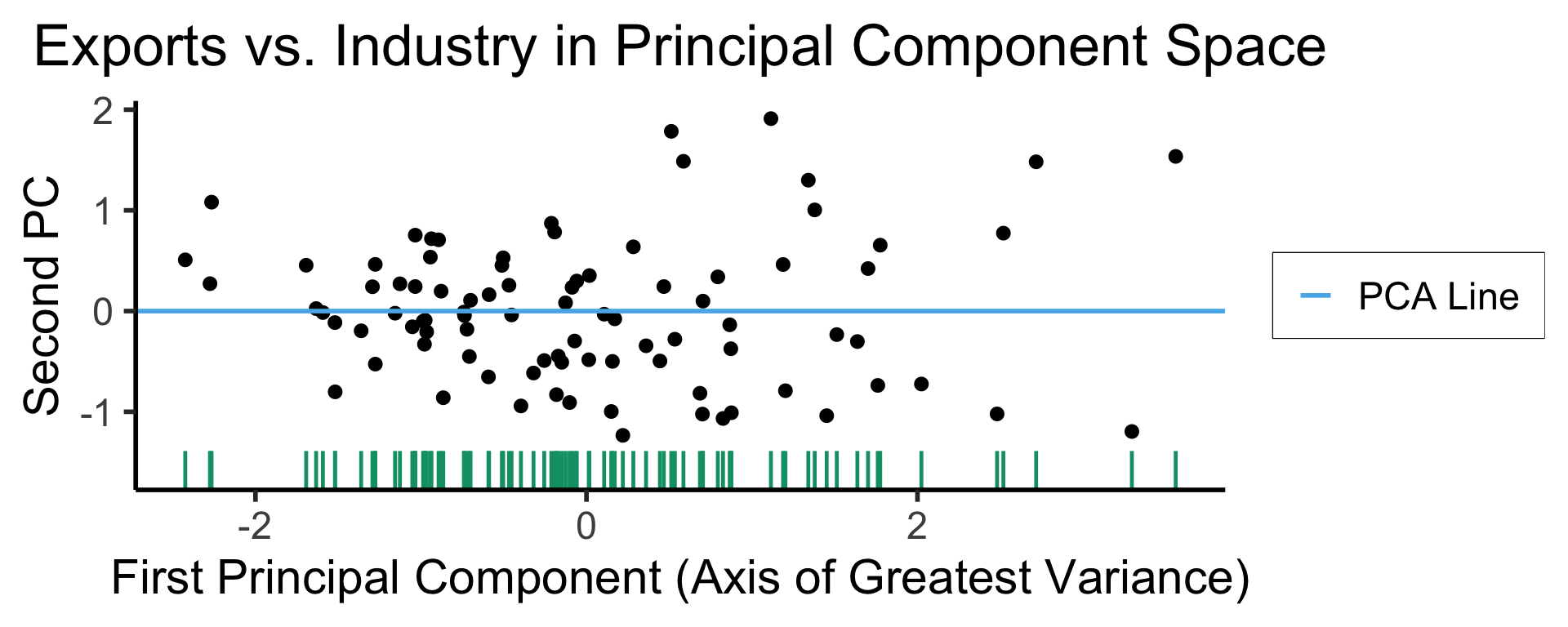
ggplot(gdp_df, aes(pc1, .fittedPC2)) +
    geom_point(size = g_pointsize/2) +
    geom_hline(aes(yintercept=0, color='PCA Line'), linetype='solid', size=g_linesize) +
    geom_rug(sides = "b", linewidth=g_linewidth/1.2, length = unit(0.1, "npc"), color=cbPalette[3]) +
    expand_limits(y=-1.6) +
    scale_color_manual(element_blank(), values=c("PCA Line"=cbPalette[2])) +
    dsan_theme("half") +
    remove_legend_title() +
    labs(
      title = "Exports vs. Industry in Principal Component Space",
      x = "First Principal Component (Axis of Greatest Variance)",
      y = "Second PC"
    )

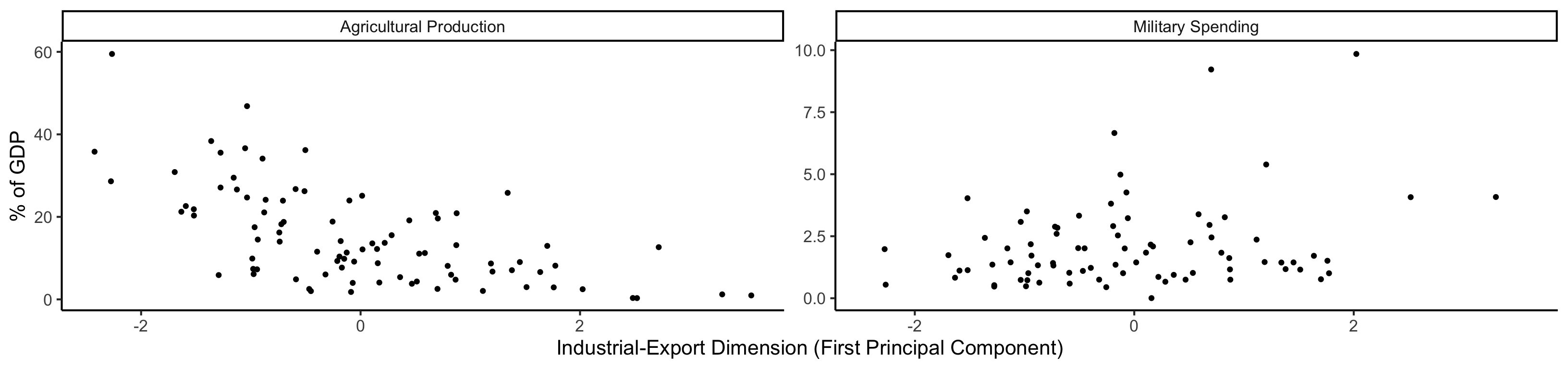
Code 
library(tidyverse) |> suppressPackageStartupMessages()
plot_df <- gdp_df |> dplyr::select(country_code, pc1, agriculture, military)
long_df <- plot_df |> pivot_longer(!c(country_code, pc1), names_to = "var", values_to = "val")
long_df <- long_df |> mutate(
  var = case_match(
    var,
    "agriculture" ~ "Agricultural Production",
    "military" ~ "Military Spending"
  )
)
ggplot(long_df, aes(x = pc1, y = val, facet = var)) +
    geom_point() +
    facet_wrap(vars(var), scales = "free") +
    dsan_theme("full") +
    labs(
        x = "Industrial-Export Dimension (First Principal Component)",
        y = "% of GDP"
    )

PCA Math Magic

  • Remember that our goal is to find the axes along which the data has greatest variance (out of all possible axes)
  • Let’s create a dataset using a known data-generating process: one dimension with 75% of the total variance, and the second with 25%:
Code 
library(tidyverse)
library(MASS)
library(ggforce)
N <- 300
Mu <- c(0, 0)
var_x <- 3
var_y <- 1
Sigma <- matrix(c(var_x, 0, 0, var_y), nrow=2)
data_df <- as_tibble(mvrnorm(N, Mu, Sigma, empirical=TRUE))
colnames(data_df) <- c("x","y")
# data_df <- data_df |> mutate(
#   within_5 = x < 5,
#   within_sq5 = x < sqrt(5)
# )
#nrow(data_df |> filter(within_5)) / nrow(data_df)
#nrow(data_df |> filter(within_sq5)) / nrow(data_df)
# And plot
ggplot(data_df, aes(x=x, y=y)) +
  # 68% ellipse
  # stat_ellipse(geom="polygon", type="norm", linewidth=g_linewidth, level=0.68, fill=cbPalette[1], alpha=0.5) +
  # stat_ellipse(type="norm", linewidth=g_linewidth, level=0.68) +
  geom_ellipse(
    aes(x0=0, y0=0, a=var_x, b=var_y, angle=0),
    linewidth = g_linewidth
  ) +
  # geom_ellipse(
  #   aes(x0=0, y0=0, a=sqrt(5), b=1, angle=0),
  #   linewidth = g_linewidth,
  #   geom="polygon",
  #   fill=cbPalette[1], alpha=0.2
  # ) +
  # # 95% ellipse
  # stat_ellipse(geom="polygon", type="norm", linewidth=g_linewidth, level=0.95, fill=cbPalette[1], alpha=0.25) +
  # stat_ellipse(type="norm", linewidth=g_linewidth, level=0.95) +
  # # 99.7% ellipse
  # stat_ellipse(geom='polygon', type="norm", linewidth=g_linewidth, level=0.997, fill=cbPalette[1], alpha=0.125) +
  # stat_ellipse(type="norm", linewidth=g_linewidth, level=0.997) +
  # Lines at x=0 and y=0
  geom_vline(xintercept=0, linetype="dashed", linewidth=g_linewidth / 2) +
  geom_hline(yintercept=0, linetype="dashed", linewidth = g_linewidth / 2) +
  geom_point(
    size = g_pointsize / 3,
    #alpha=0.5
  ) +
  geom_rug(length=unit(0.5, "cm"), alpha=0.75) +
  geom_segment(
    aes(x=-var_x, y=0, xend=var_x, yend=0, color='PC1'),
    linewidth = 1.5 * g_linewidth,
    arrow = arrow(length = unit(0.1, "npc"))
  ) +
  geom_segment(
    aes(x=0, y=-var_y, xend=0, yend=var_y, color='PC2'),
    linewidth = 1.5 * g_linewidth,
    arrow = arrow(length = unit(0.1, "npc"))
  ) +
  dsan_theme("half") +
  coord_fixed() +
  remove_legend_title() +
  scale_color_manual(
    "PC Vectors",
    values=c('PC1'=cbPalette[1], 'PC2'=cbPalette[2])
  ) +
  scale_x_continuous(breaks=seq(-5,5,1), limits=c(-5,5))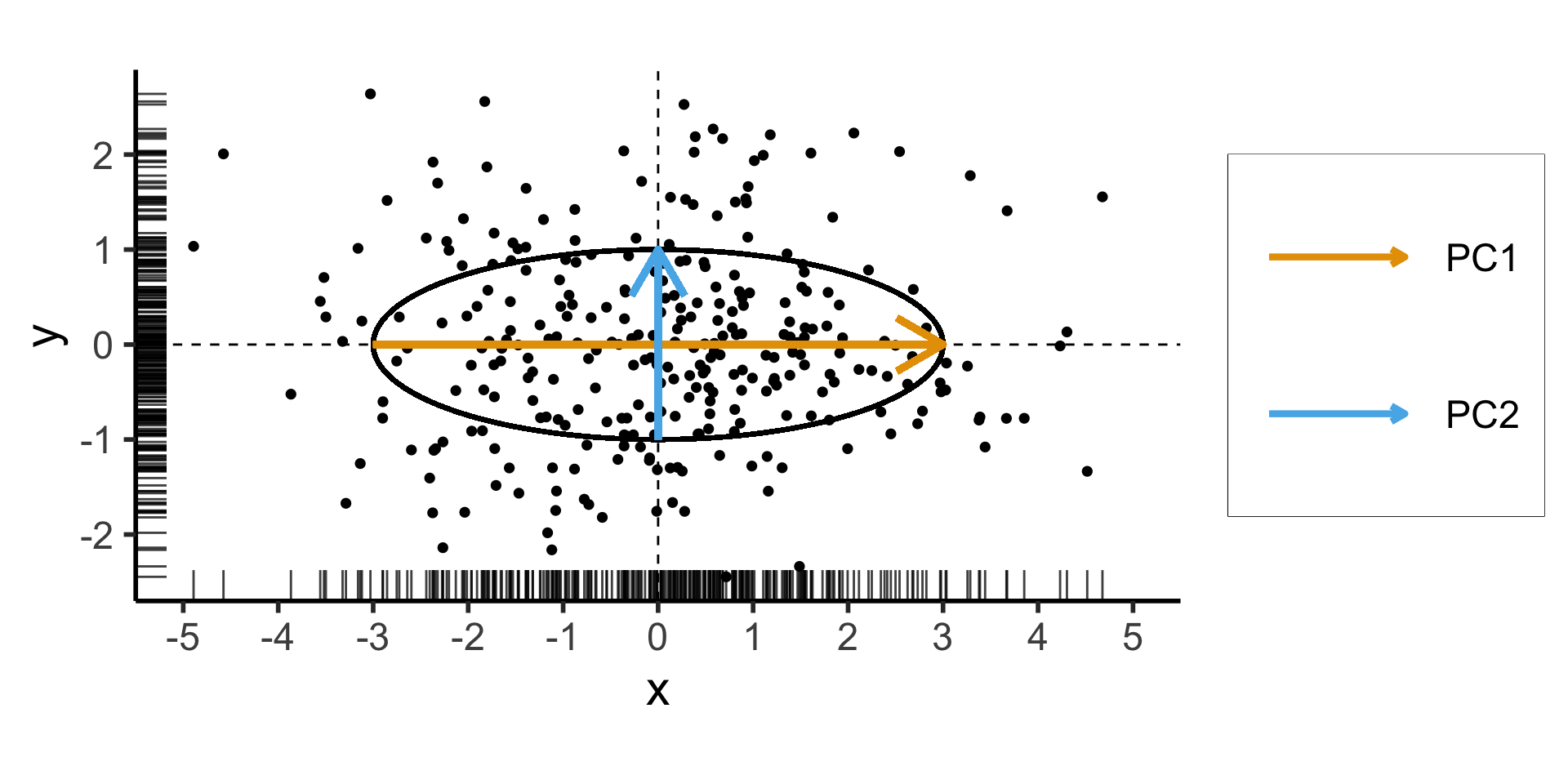

\[ \mathbf{\Sigma} = \begin{bmatrix} {\color{#e69f00}3} & 0 \\ 0 & {\color{#56b4e9}1} \end{bmatrix} \]

Two solutions to \(\mathbf{\Sigma}\mathbf{x} = \lambda \mathbf{x}\):

  • \({\color{#e69f00}\lambda_1} = 3, {\color{#e69f00}\mathbf{x}_1} = (1, 0)^\top\)
  • \({\color{#56b4e9}\lambda_2} = 1, {\color{#56b4e9}\mathbf{x}_2} = (0, 1)^\top\)

Now With PCA Lines \(\neq\) Axes

  • We now introduce covariance between \(x\) and \(y\) coordinates of our data:
Code 
library(tidyverse)
library(MASS)
N <- 250
Mu <- c(0,0)
Sigma <- matrix(c(2,1,1,2), nrow=2)
data_df <- as_tibble(mvrnorm(N, Mu, Sigma))
colnames(data_df) <- c("x","y")
# Start+end coordinates for the transformed vectors
pc1_rc <- (3/2)*sqrt(2)
pc2_rc <- (1/2)*sqrt(2)
ggplot(data_df, aes(x=x, y=y)) +
  geom_ellipse(
    aes(x0=0, y0=0, a=var_x, b=var_y, angle=pi/4),
    linewidth = g_linewidth,
    #fill='grey', alpha=0.0075
  ) +
  geom_vline(xintercept=0, linetype="dashed", linewidth=g_linewidth / 2) +
  geom_hline(yintercept=0, linetype="dashed", linewidth = g_linewidth / 2) +
  geom_point(
    size = g_pointsize / 3,
    #alpha=0.7
  ) +
  geom_rug(
    length=unit(0.35, "cm"), alpha=0.75
  ) +
  geom_segment(
    aes(x=-pc1_rc, y=-pc1_rc, xend=pc1_rc, yend=pc1_rc, color='PC1'),
    linewidth = 1.5 * g_linewidth,
    arrow = arrow(length = unit(0.1, "npc"))
  ) +
  geom_segment(
    aes(x=pc2_rc, y=-pc2_rc, xend=-pc2_rc, yend=pc2_rc, color='PC2'),
    linewidth = 1.5 * g_linewidth,
    arrow = arrow(length = unit(0.1, "npc"))
  ) +
  dsan_theme("half") +
  remove_legend_title() +
  coord_fixed() +
  scale_x_continuous(breaks=seq(-4,4,2))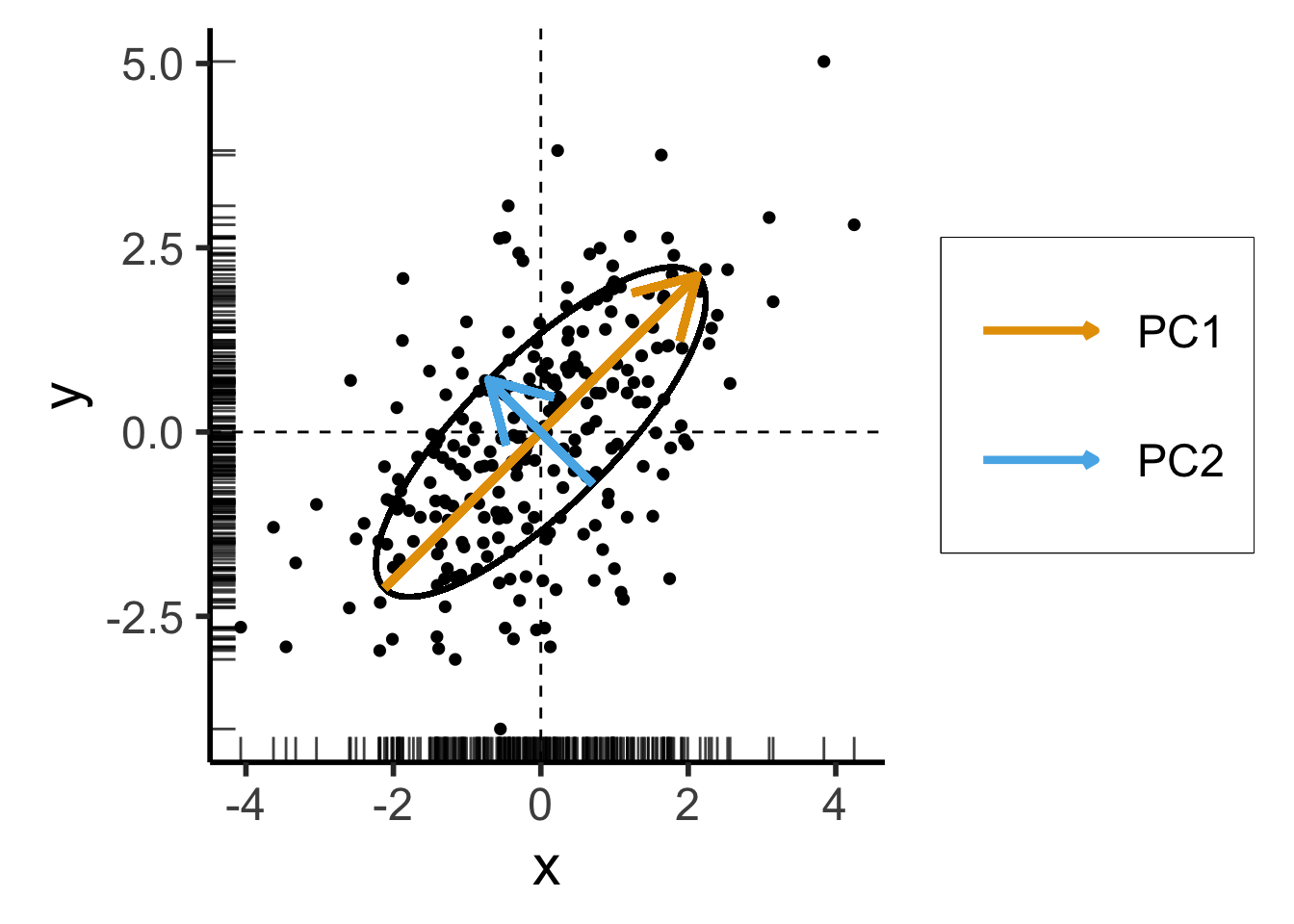

\[ \mathbf{\Sigma}' = \begin{bmatrix} 2 & 1 \\ 1 & 2 \end{bmatrix} \]

Still two solutions to \(\mathbf{\Sigma}'\mathbf{x} = \lambda \mathbf{x}\):

  • \({\color{#e69f00}\lambda_1} = 3, {\color{#e69f00}\mathbf{x}_1} = (1,1)^\top\)
  • \({\color{#56b4e9}\lambda_2} = 1, {\color{#56b4e9}\mathbf{x}_2} = (-1,1)^\top\)

PCA and Eigenvalues

Takeaway 1: Regardless of the coordinate system,

  • Eigenvectors give us axes of greatest variance: \(\mathbf{x}_1\) is axis of greatest variance, \(\mathbf{x}_2\) is axis of 2nd-greatest variance, etc.
  • The corresponding Eigenvalues tell us how much of the total variance is explained by this axis

PCA as Swiss Army Knife

  • PCA can be used for both reinterpretation and reduction of dimensions!
  • Consider dataset \(\mathbf{X} = (X_1, \ldots, X_n)\), with \(X_i \in \mathbb{R}^N\)
Reinterpretation

If we project each \(X_i\) onto \(N\) principal component axes:

  • Datapoints in PC space are linear combinations of the original datapoints! (← Takeaway 2a)

    \[ X'_i = \alpha_1X_1 + \cdots + \alpha_nX_n, \]

    where \(\forall i \left[\alpha_i \neq 0\right]\)

  • We are just “re-plotting” our original data in PC space via change of coordinates

  • Thus we can recover the original data from the PC data

Reduction

If we project \(X_i\) onto \(M < N\) principal component axes:

  • Datapoints in PC space are still linear combinations of the original datapoints (← Takeaway 2b), but now some of the scalars (weights) are 0
  • We have performed statistically-principled dimensionality reduction (← Takeaway 3)
  • However, original data cannot be recovered

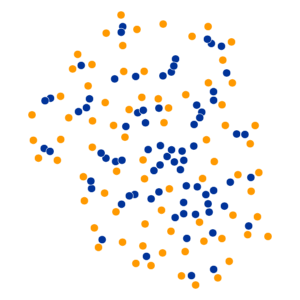
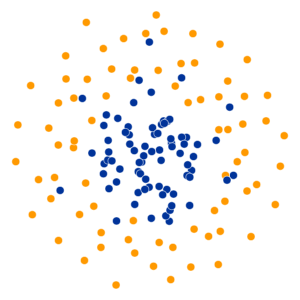
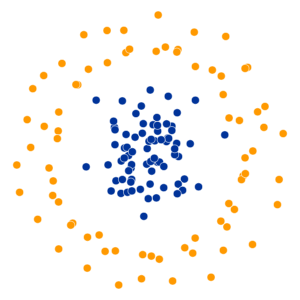
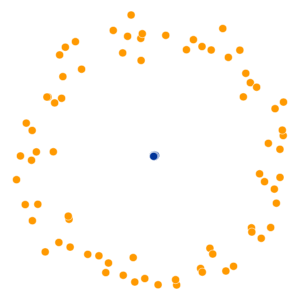
t-SNE for Dimensionality Reduction

  • t-Distributed Stochastic Neighbor Embedding (Van der Maaten and Hinton 2008)
  • If \(x, y\) are neighbors in \(\mathbb{R}^{1000}\), t-SNE “succeeds” if they remain neighbors in \(\mathbb{R}^2\)
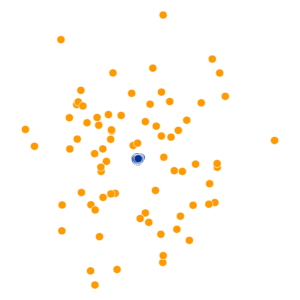
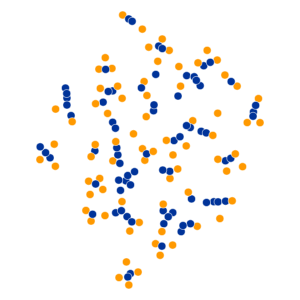
  • Key hyperparameter: perplexity! Roughly, this affects the “tradeoff” between preserving local structure vs. global structure in the lower-dimensional space
  • Choose \(x_i \in \mathbb{R}^{1000}\), and treat it as the center of a Gaussian ball with variance \(\sigma_i\)
  • The choice of \(\sigma_i\) induces a probability distribution \(P_i\) over all other points (what is the probability of drawing \(x_j\) from \(\mathcal{N}(x_i, \sigma_i)\)?)

\[ \text{Perp}(P_i) = 2^{H(P_i)} \]

  • High perplexity \(\iff\) high entropy (eventually Gaussian ball will grow so big that all other points will be equally likely!). So, vary perplexity, see how plot changes

  • See here for an absolutely incredible interactive walkthrough of t-SNE!

What Happens As We Vary Perplexity?

Original Dataset

Perplexity = 2

Perplexity = 5

Perplexity = 30

 

Perplexity = 50

 

Perplexity = 100

 

References

Choi, Sungmun. 2017. “Politician’s Ideology and Campaign Contributions from Interest Groups.” Empirical Economics 53 (4): 1733–46. https://doi.org/10.1007/s00181-016-1168-3.
Noel, Hans. 2014. Political Ideologies and Political Parties in America. Cambridge University Press.
Tibshirani, Robert, Guenther Walther, and Trevor Hastie. 2001. “Estimating the Number of Clusters in a Data Set via the Gap Statistic.” Journal of the Royal Statistical Society. Series B (Statistical Methodology) 63 (2): 411–23. https://www.jstor.org/stable/2680607.
Van der Maaten, Laurens, and Geoffrey Hinton. 2008. “Visualizing Data Using t-SNE.” Journal of Machine Learning Research 9 (11).

Appendix: Uniform Sampling From A Triangle

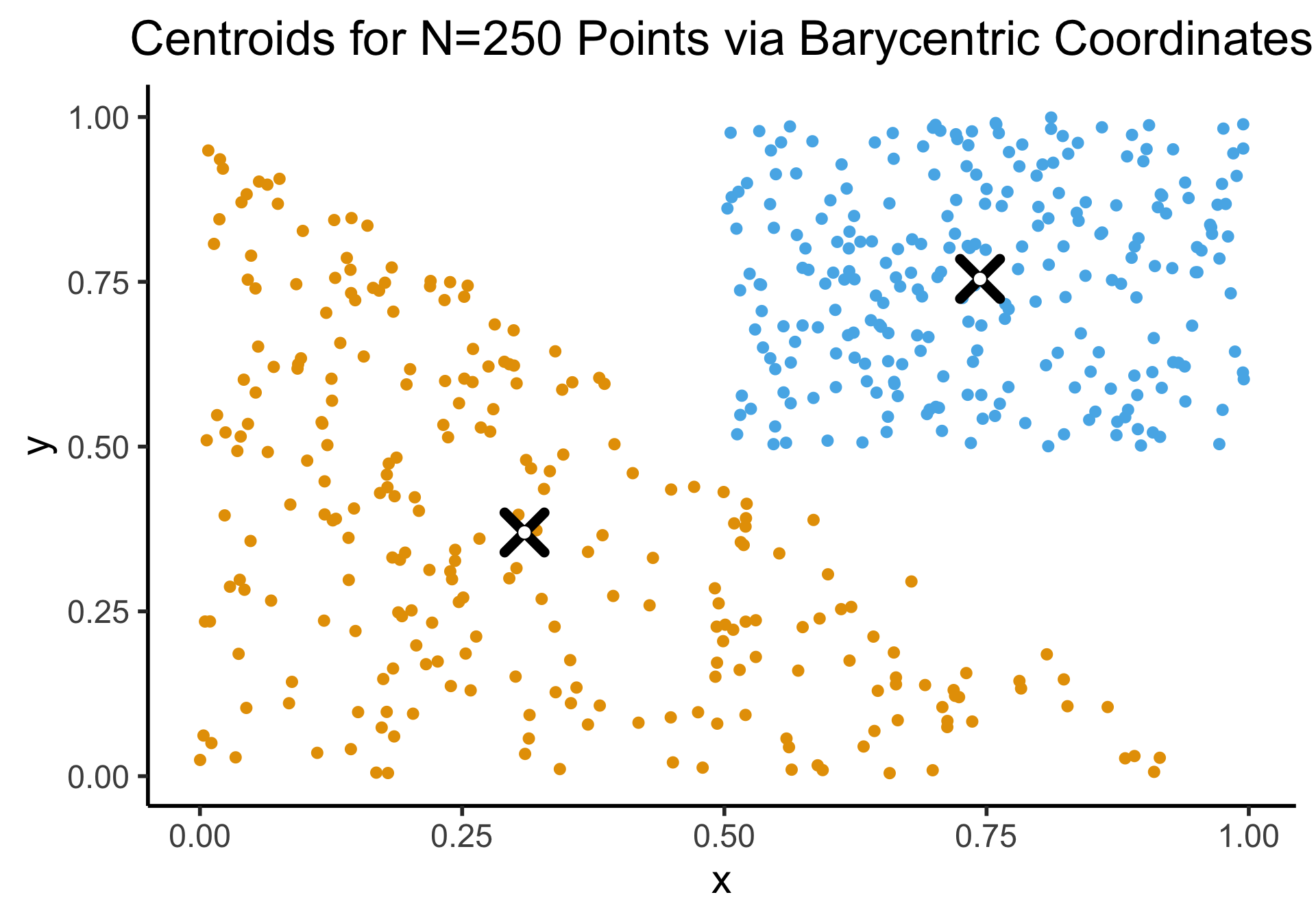
  • See here for how the K-Means Clustering: Centroids slide sampled uniformly from \(\triangle\)!
  • If you don’t use the Barycentric coordinate transformation (right), your points will be clustered more heavily towards the bottom-right of the triangle (left), and the centroid of the sampled points will not be the actual centroid of the triangle!
Code 
N <- 250
x_coords <- runif(N, 0, 1)
y_coords <- runif(N, 0, 1 - x_coords)
data_df <- tibble(x=x_coords, y=y_coords)
cent_x <- mean(x_coords)
cent_y <- mean(y_coords)
cent_df <- tibble(x=cent_x, y=cent_y)
triangle_plot <- ggplot(
    data_df,
    aes(x=x, y=y)
  ) +
  geom_point(
    size = g_pointsize / 2,
    color=cbPalette[1]
  ) +
  geom_point(
    data=cent_df,
    aes(x=x, y=y),
    shape=4, stroke=4, color='black',
    size = g_pointsize * 1.5) +
  geom_point(
    data=cent_df,
    aes(x=x, y=y),
    shape=19, color='white',
    size = g_pointsize / 2) +
  dsan_theme('quarter')
# Now a rectangle
x_coords_rect <- runif(N, 0.5, 1)
y_coords_rect <- runif(N, 0.5, 1)
rect_df <- tibble(x=x_coords_rect, y=y_coords_rect)
cent_x_rect <- mean(x_coords_rect)
cent_y_rect <- mean(y_coords_rect)
cent_df_rect <- tibble(x=cent_x_rect, y=cent_y_rect)
rect_plot <- triangle_plot +
  geom_point(
    data=rect_df,
    aes(x=x, y=y),
    size = g_pointsize / 2,
    color=cbPalette[2]
  ) +
  geom_point(
    data=cent_df_rect,
    aes(x=x, y=y),
    shape=4, stroke=4, color='black',
    size = g_pointsize * 1.5) +
  geom_point(
    data=cent_df_rect,
    aes(x=x, y=y),
    shape=19, color='white',
    size = g_pointsize / 2) +
  dsan_theme('half') +
  labs(
    title = "Centroids for N=250 Points: Y ~ U[0,X]"
  )
rect_plot 
N <- 250
r1_vals <- runif(N, 0, 1)
r2_vals <- runif(N, 0, 1)
triangle_df <- tibble(r1=r1_vals, r2=r2_vals)
v1 <- c(0,0)
v2 <- c(1,0)
v3 <- c(0,1)
triangle_df <- triangle_df |> mutate(
    bary_w1 = 1 - sqrt(r1),
    bary_w2 = sqrt(r1) * (1 - r2),
    bary_w3 = sqrt(r1) * r2
)
triangle_df <- triangle_df |> mutate(
    x = bary_w1 * v1[1] + bary_w2 * v2[1] + bary_w3 * v3[1],
    y = bary_w1 * v1[2] + bary_w2 * v2[2] + bary_w3 * v3[2]
)
triangle_cent_x <- mean(triangle_df$x)
triangle_cent_y <- mean(triangle_df$y)
triangle_cent_df <- tibble(x=triangle_cent_x, y=triangle_cent_y)
triangle_plot <- ggplot(
    triangle_df,
    aes(x=x, y=y)
  ) +
  geom_point(
    size = g_pointsize / 2,
    color=cbPalette[1]
  ) +
  geom_point(
    data=triangle_cent_df,
    aes(x=x, y=y),
    shape=4, stroke=4, color='black',
    size = g_pointsize * 1.5) +
  geom_point(
    data=triangle_cent_df,
    aes(x=x, y=y),
    shape=19, color='white',
    size = g_pointsize / 2) +
  dsan_theme('quarter')
# Now a rectangle
x_coords_rect <- runif(N, 0.5, 1)
y_coords_rect <- runif(N, 0.5, 1)
rect_df <- tibble(x=x_coords_rect, y=y_coords_rect)
cent_x_rect <- mean(x_coords_rect)
cent_y_rect <- mean(y_coords_rect)
cent_df_rect <- tibble(x=cent_x_rect, y=cent_y_rect)
rect_plot <- triangle_plot +
  geom_point(
    data=rect_df,
    aes(x=x, y=y),
    size = g_pointsize / 2,
    color=cbPalette[2]
  ) +
  geom_point(
    data=cent_df_rect,
    aes(x=x, y=y),
    shape=4, stroke=4, color='black',
    size = g_pointsize * 1.5) +
  geom_point(
    data=cent_df_rect,
    aes(x=x, y=y),
    shape=19, color='white',
    size = g_pointsize / 2) +
  dsan_theme('half') +
  labs(
    title = "Centroids for N=250 Points via Barycentric Coordinates"
  )
rect_plot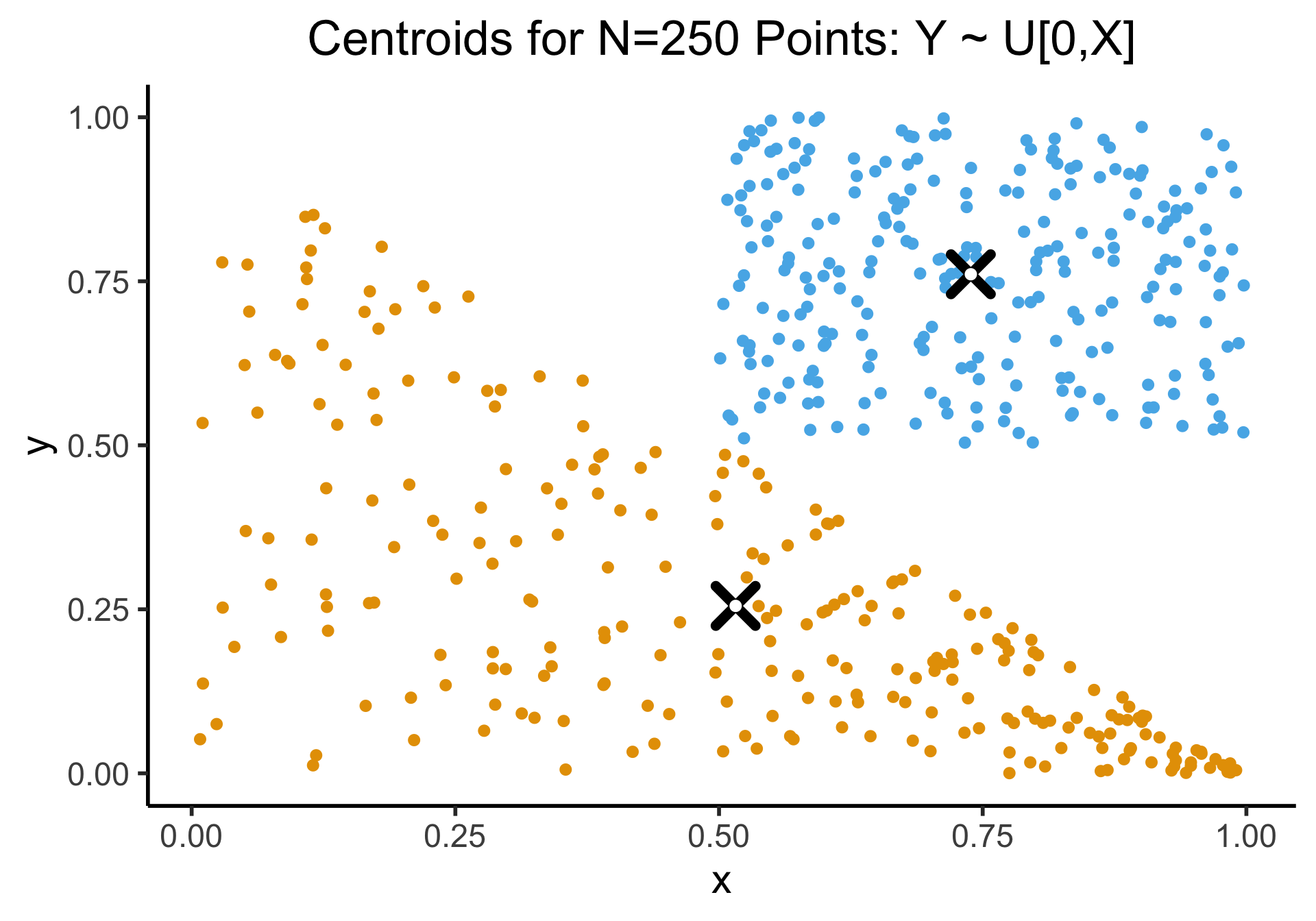

DSAN 5000 W09: Dimensionality Reduction