Week 7: Python Functions and Control Flow, Law of Large Numbers

DSUA111: Data Science for Everyone, NYU, Fall 2020

TA Jeff, jpj251@nyu.edu

Outline

[Part 1: Python]

  1. Functions
  2. Conditional Statements
  3. Loops

[Part 2: Not Python]

  1. Sampling and Law of Large Numbers

Part 1: Python

Functions

  • Built-In Functions
  • Imported Functions
  • Make Your Own!

Built-In Functions

In [90]:
print("hi")

hi
In [92]:
float("infinity")
Out[92]:
inf
In [93]:
type(float("infinity"))
Out[93]:
float

Imported Functions

In [94]:
my_list = [1,2,3,4,5]
In [95]:
my_list.sum()

---------------------------------------------------------------------------
AttributeError                            Traceback (most recent call last)
<ipython-input-95-ed142f2087a1> in <module>
----> 1 my_list.sum()

AttributeError: 'list' object has no attribute 'sum'

noooooooooo

In [96]:
import numpy as np
In [97]:
my_array = np.array(my_list)
In [98]:
my_array.sum()
Out[98]:
15

yayyyyyyyyyy

Make Your Own!

In [99]:
def how_many_letters():
    return len("abcdefghijklmnopqrstuvwxyz")

...No output?

In [100]:
how_many_letters()
Out[100]:
26

What does this function return?

In [163]:
fn_result = how_many_letters()
print(fn_result)

26
In [164]:
print(type(fn_result))

<class 'int'>

Printing Is Not Returning!!!

In [104]:
def say_hi():
    print("hi")
In [105]:
say_hi()

hi

What does this function return?

In [106]:
hi_result = say_hi()

hi
In [107]:
print(hi_result)

None
In [108]:
print(type(hi_result))

<class 'NoneType'>

Instead...

In [109]:
def return_hi():
    return "hi"
In [110]:
return_hi()
Out[110]:
'hi'

What does this function return?

In [111]:
hi_result_2 = return_hi()
In [112]:
print(hi_result_2)

hi
In [113]:
print(type(hi_result_2))

<class 'str'>

I know this is a ten year old meme and that teachers using memes is one of the lamest things in the universe but... i had to do it

Make Your Own! With Parameters!

In [114]:
def triple(the_number):
    return 3 * the_number
In [115]:
triple(5)
Out[115]:
15
In [117]:
triple(0)
Out[117]:
0
In [116]:
triple(triple(5))
Out[116]:
45

Can do more than one!

In [139]:
def combine_names(first_name, second_name, third_name):
    return first_name + ", " + second_name + ", and " + third_name
In [141]:
combine_names("Alice", "Bob", "Craig")
Out[141]:
'Alice, Bob, and Craig'

(https://en.wikipedia.org/wiki/Alice_and_Bob)

Conditional Statements

  • Called "Control Flow Statements" (https://en.wikipedia.org/wiki/Control_flow)
  • Until now, Python ran every line you wrote, from top of cell to bottom, in order
  • Now you can control which lines get run, conditionally
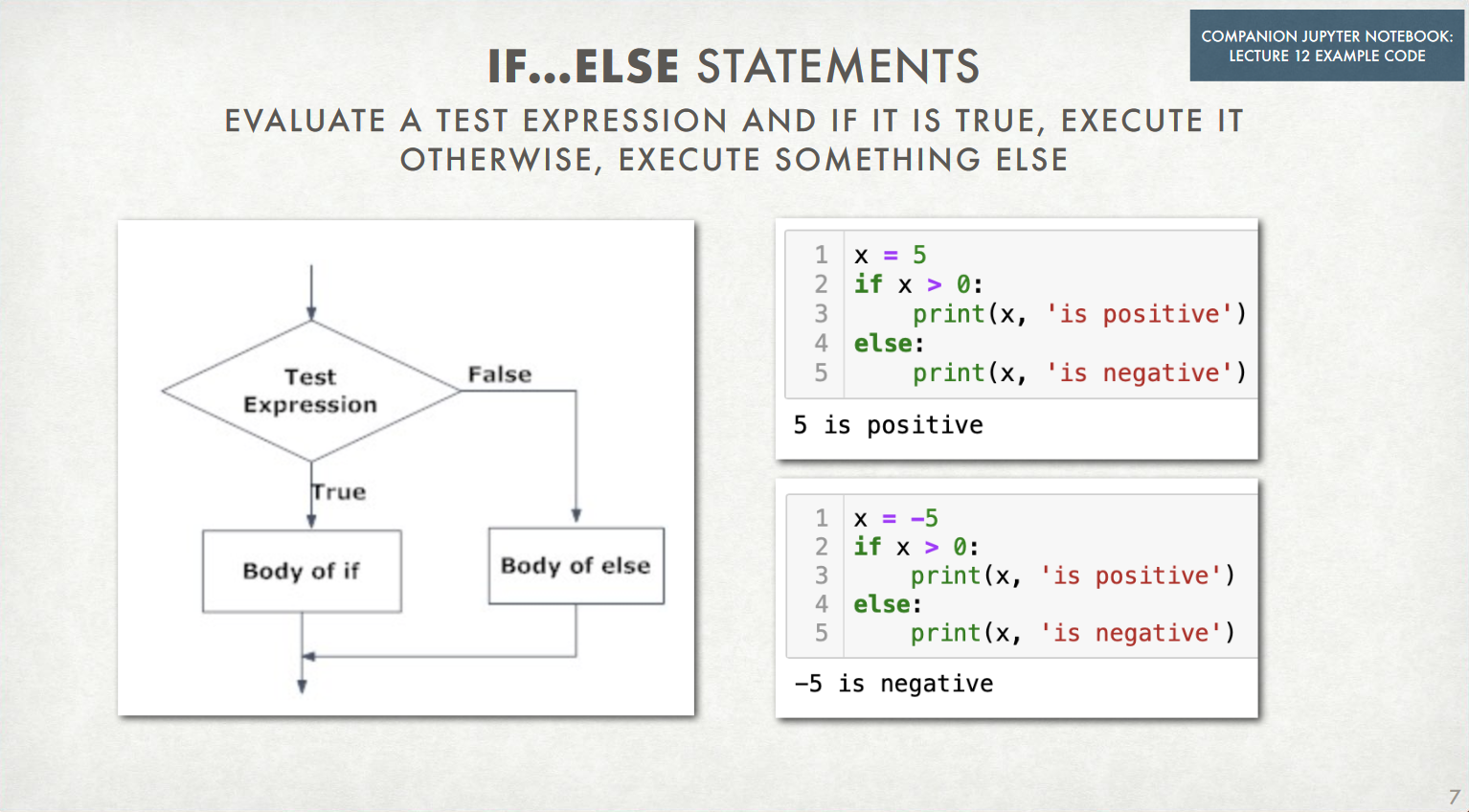
  • if, if-else, if-elif-else (really if-elif-...-elif-else)

if Statements

if condition:
    expression(s)

(Lecture 12.3, Slide 6)

if-else

if condition_1:
    expression_1
else:
    expression_2

(Lecture 12.3, Slide 7)

if-elif-...-elif-else

if condition_1:
    expression_1
elif condition_2:
    expression_2
...
elif condition_10:
    expression_10
else:
    expression_11

(Lecture 12.3, Slide 8)

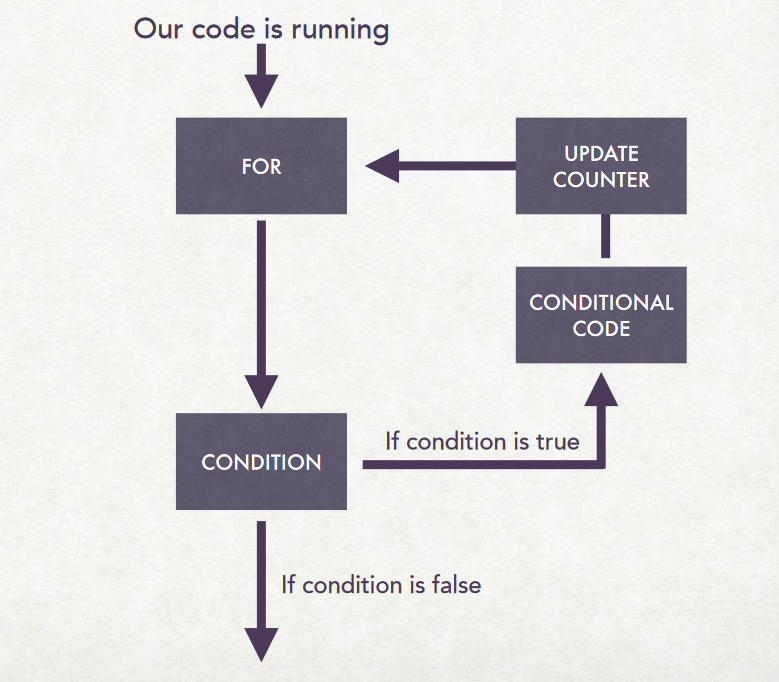
while Loops

while condition:
    expression

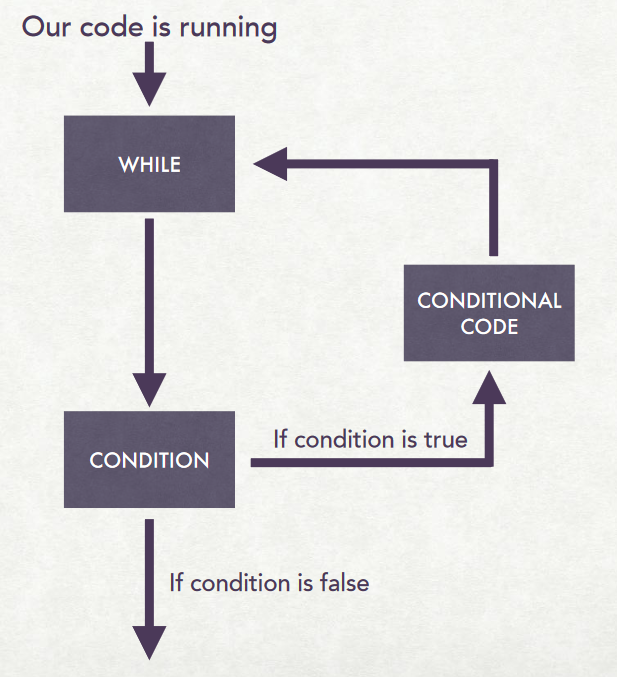
(Lecture 12.2, Slide 12)

(tl;dr: While $X$ is true, do $Y$)

In [165]:
i = 0
while i < 10:
    print(i)
    i = i + 1

0
1
2
3
4
5
6
7
8
9
In [166]:
my_list = ["Afghanistan", "Albania", "Algeria", "Yemen", "Zambia", "Zimbabwe"]
In [167]:
list_index = 0
while list_index < len(my_list):
    current_thing = my_list[list_index]
    print("Item #" + str(list_index) + " is " + str(current_thing))
    list_index = list_index + 1

Item #0 is Afghanistan
Item #1 is Albania
Item #2 is Algeria
Item #3 is Yemen
Item #4 is Zambia
Item #5 is Zimbabwe

That's a lot of gross-looking code...

for Loops

for element in sequence:
    expression

(tl;dr: For each thing in $X$, do $Y$)

In [142]:
for current_thing in my_list:
    print(current_thing)

Afghanistan
Albania
Algeria
Yemen
Zambia
Zimbabwe
In [143]:
for list_index, current_thing in enumerate(my_list):
    print("Element #" + str(list_index) + " is " + str(current_thing))

Element #0 is Afghanistan
Element #1 is Albania
Element #2 is Algeria
Element #3 is Yemen
Element #4 is Zambia
Element #5 is Zimbabwe

Part 2: Not Python

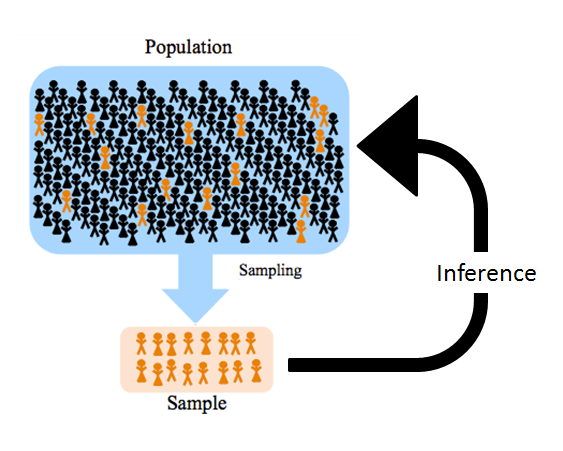
Sampling

  • Population: Full set of things we want to draw inferences about
  • Sample: Actual set of observations of these things that we have to work with

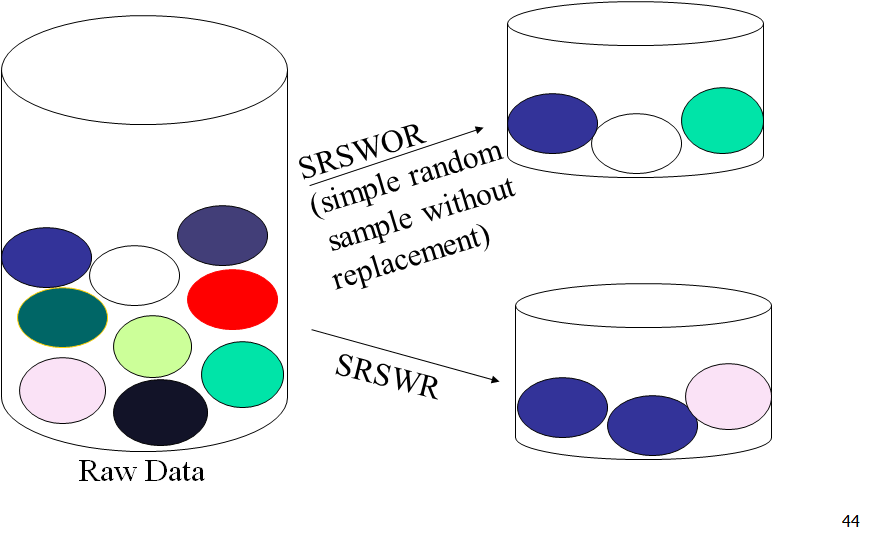
(from https://www.statsandr.com/blog/what-is-the-difference-between-population-and-sample/)

Sampling With and Without Replacement

  • Sampling With Replacement: People/units can enter the sample more than once
  • Sampling Without Replacement: People/units enter the same at most once

(from https://slidewiki.org/deck/1290-2/data-reduction/slide/10562-2/10562-2:21/view)

Distributions

  • Probability Distribution: Theoretical -- I expect that each side of the die will come up 1/6th of the time
  • Empirical Distribution: Actually observed -- I rolled the die 10 times and saw this many 1s, this many 2s, ...

Plotting a Distribution

In [188]:
import matplotlib.pyplot as plt
def plot_distribution():
    die_faces = [1,2,3,4,5,6]
    probabilities = [1/6,1/6,1/6,1/6,1/6,1/6]
    plt.bar(die_faces, probabilities)
    plt.show()
In [189]:
plot_distribution()
In [175]:
1/6
Out[175]:
0.16666666666666666

Law of Large Numbers

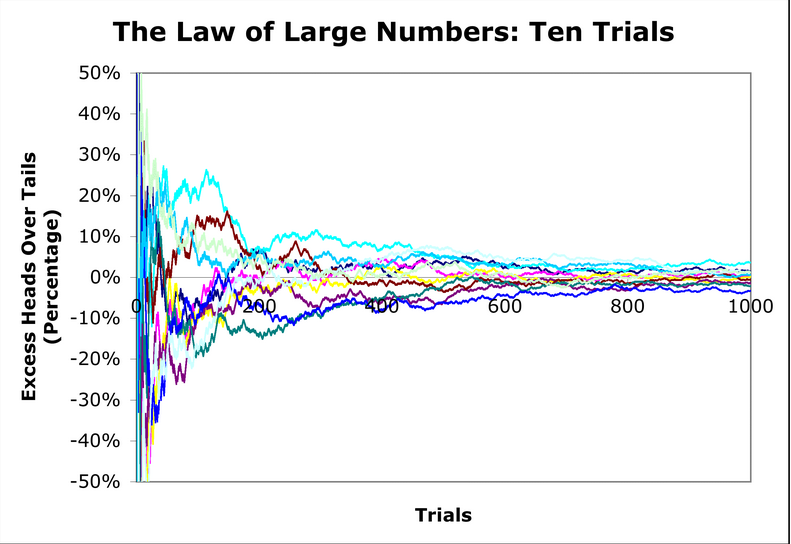
(from https://alphaarchitect.com/2014/01/04/the-law-of-large-numbers-and-casino-earnings/)

N = 10

In [148]:
import numpy as np
In [182]:
# N = 10
rolls = np.random.randint(1, 7, 10)
print(rolls)
more_rolls = np.random.randint(1, 7, 10)
print(more_rolls)
even_more_rolls = np.random.randint(1, 7, 10)
print(even_more_rolls)

[2 2 4 3 1 6 2 1 2 6]
[2 6 5 5 4 5 3 4 6 6]
[5 2 3 3 6 6 3 3 2 5]
In [183]:
plt.hist(rolls, bins=range(1,8))
plt.show()
In [184]:
plt.hist(more_rolls, bins=range(1,8))
plt.show()
In [185]:
plt.hist(even_more_rolls, bins=range(1,8))
plt.show()

N = 100

In [187]:
rolls_100 = np.random.randint(1, 7, 100)
print(rolls_100)
more_rolls_100 = np.random.randint(1, 7, 100)
print(more_rolls_100)
even_more_rolls_100 = np.random.randint(1, 7, 100)
print(even_more_rolls_100)

[1 4 5 6 3 2 3 3 6 4 1 6 5 5 1 1 3 5 5 4 4 2 1 3 4 6 5 6 4 4 1 2 3 4 2 1 6
 6 6 2 1 1 3 2 3 5 3 4 2 1 1 3 5 5 3 6 1 2 6 5 1 4 6 3 4 3 1 6 3 2 6 3 1 3
 6 1 4 2 3 6 3 6 5 5 3 1 3 6 4 4 1 1 3 2 5 6 6 5 4 4]
[3 4 5 5 3 6 1 4 1 1 5 4 1 6 5 3 1 4 5 4 1 3 2 1 2 4 3 6 4 2 4 4 3 4 6 5 5
 2 5 1 5 5 1 5 4 6 3 2 2 6 6 3 2 2 3 5 4 1 3 1 1 6 2 6 2 6 5 1 4 5 2 6 1 3
 2 1 1 4 6 6 3 5 5 1 2 4 4 1 5 2 2 3 5 6 6 4 5 2 5 4]
[2 1 3 2 1 5 5 5 5 3 3 4 4 6 6 5 6 5 3 6 3 2 2 6 4 2 1 6 6 4 2 6 5 1 3 2 1
 4 1 6 3 6 5 1 5 3 4 6 4 4 6 1 3 3 4 1 1 6 1 1 1 5 1 2 1 5 6 6 3 4 3 3 1 6
 6 3 5 1 1 4 6 6 4 6 4 5 4 4 5 4 5 4 4 2 5 2 3 2 3 4]
In [154]:
plt.hist(rolls_100, bins=range(1,8))
plt.show()
In [155]:
plt.hist(more_rolls_100, bins=range(1,8))
plt.show()

Hmmmm... it's getting really tedious to make 2, 3, 4 rolls variables each time... did we learn something that could help us here?

In [191]:
i = 0
while i < 3:
    current_roll_100 = np.random.randint(1, 7, 100)
    plt.hist(current_roll_100, bins=range(1,8))
    plt.show()
    i = i + 1
print("Done!")

Done!

<Figure size 432x288 with 0 Axes>

Now smash that sample size increase button

N = 1,000

In [157]:
plt.hist(np.random.randint(1, 7, 1000), bins=range(1,8))
plt.show()

Again, getting super tired of writing this same basic code over and over again... wonder if there's ANOTHER thing we learned that could help us here?

In [158]:
def plot_dice_rolls(N):
    rolls_N = np.random.randint(1, 7, N)
    plt.hist(rolls_N, bins=range(1,8))
    plt.show()

N = 10,000

In [170]:
plot_dice_rolls(10000)

N = 100,000

In [169]:
plot_dice_rolls(100000)

N = 1 Million

In [168]:
plot_dice_rolls(1000000)

Recall the Probability Distribution...

In [180]:
plot_distribution()