Week 4: Causality Wrap-Up, Python Sequences and Libraries

DSUA111: Data Science for Everyone, NYU, Fall 2020

TA Jeff, jpj251@nyu.edu

• This slideshow: https://jjacobs.me/dsua111-sections/week-04
• All materials: https://github.com/jpowerj/dsua111-sections

Outline

1. HW1 Feedback
2. Causality Wrap-Up
3. Python Sequences
4. Python Libraries

0. HW1 Feedback

• NYU Classes -> Gradebook

1. Causality Wrap-Up

Where we left off:

Fundamental Problem of Causal Inference: Forget Everything And Run?

Face Everything And Rise

• Find good comparison cases: Treatment Group and Control Group

• "Statistical Matching"
  • Don't worry about the details, but tldr is:
  • Find the two most similar people, put one in Treatment Group, the other in Control Group, and compare their outcomes
  • Bam. If we can measure and take into account all variables that may be related to our causal hypothesis, this is as close as we can possibly get to "solving" FPCI
  • [Not on the midterm or final, but relevant in case you're despairing about FPCI]

Controlled Experiments: How/Why Do They Help?

• Random Assignment: Vietnam War/Second Indochina War Draft
  • Key point: makes treatment and control groups similar, on average, without us having to do any work!
  • (e.g., don't need to worry about "pairing up" similar treatment+control units via statistical matching)
• No more Selection Effects
• Omitted variables are in BOTH Treatment and Control groups

Complications: Selection

• Tldr: Why did this person (unit) end up in the treatment group? Why did this other person (unit) end up in the control group?
  • Are there systematic differences?
• Vietnam/Indochina Draft: Why can't we just study [men who join the military] versus [men who don't], and take the difference as a causal estimate?

Complications: Compliance

• We ideally want people assigned to the treatment group to take the treatment, and people assigned to the control group to take the control.
• "Compliance" is the degree to which this is actually true in your experiment
  • High compliance = most people actually took what they were assigned
  • Low compliance = lots of people who were assigned to treatment actually took control, and vice-versa
• What problems might there be with compliance in the Draft example?

The Biggest Complication: Observational Data

• In observational studies, researchers have no control over assignment to treatment/control 😨
• On the one hand... Forget Everything And Run, if you can.
• On the other hand... statisticians over the last ~4 centuries have developed fancy causal inference tools/techniques to help us Face Everything And Rise!

Causal Terminology for Observational Studies

(This is... genuinely important + relevant imo)

from Hu (2020), "Direct Effects"

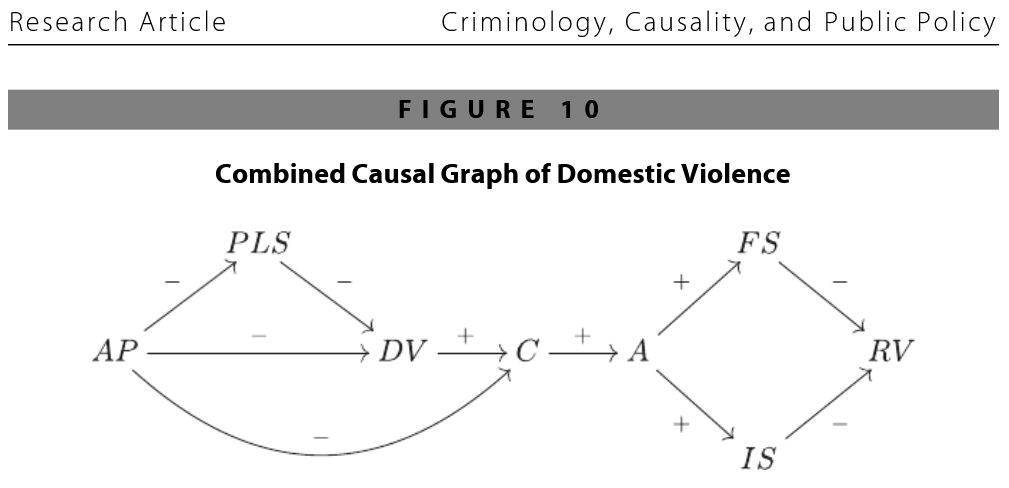
from Sampson, Winship, and Knight (2013), "Translating Causal Claims: Principles and Strategies for Policy‐Relevant Criminology"

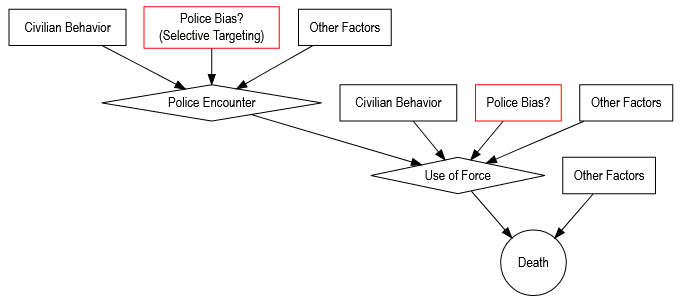
from Bradford (2020), "Observations on Police Shootings & Interracial Violence"

2. Python Sequences

Where we left off:

my_string = "Jeff"
my_float = 5.5
my_string * my_float

---------------------------------------------------------------------------
TypeError                                 Traceback (most recent call last)
<ipython-input-113-e6906dc4821b> in <module>
      1 my_string = "Jeff"
      2 my_float = 5.5
----> 3 my_string * my_float

TypeError: can't multiply sequence by non-int of type 'float'

Sequences?

(Lecture 6.2 slides, p. 5)

Jeff's TLDR

• Lists: Ordered sequences of... anything (including lists themselves 🤯)

my_basic_list = [1, "one", 1.0]
print(my_basic_list)

[1, 'one', 1.0]

my_meta_list = [my_basic_list, 2, "two", 2.0, [3, "three", 3.0]]
print(my_meta_list)

[[1, 'one', 1.0], 2, 'two', 2.0, [3, 'three', 3.0]]

• This is not the same as

my_non_meta_list = my_basic_list + [2, "two", 2.0] + [3, "three", 3.0]
print(my_non_meta_list)

[1, 'one', 1.0, 2, 'two', 2.0, 3, 'three', 3.0]

• ^(!!!)

Ordered?

• We specify "ordered" only because there are also sets, which contain elements but have no notion of a "first", "second", "third" element

ordered_list = [4, 3, 2, 1]
set(ordered_list)

{1, 2, 3, 4}

Arrays are just fancier lists (for doing fancier math)

ordered_array = np.array(ordered_list)

• What happened?

Remember to import NumPy first!

import numpy as np
ordered_array = np.array(ordered_list)
print(ordered_array)
print(ordered_list)

[4 3 2 1]
[4, 3, 2, 1]

ordered_list.mean()

---------------------------------------------------------------------------
AttributeError                            Traceback (most recent call last)
<ipython-input-120-46a02c4663bc> in <module>
----> 1 ordered_list.mean()

AttributeError: 'list' object has no attribute 'mean'

ordered_array.mean()

2.5

Important difference, though: NumPy arrays require that all elements be the same type!

...so what happens if they're different?

no_bueno = np.array([1,"two",3.0])
no_bueno

array(['1', 'two', '3.0'], dtype='<U11')

print(type(no_bueno[0]))
print(type(no_bueno[1]))
print(type(no_bueno[2]))

<class 'numpy.str_'>
<class 'numpy.str_'>
<class 'numpy.str_'>

Bracket Madness

• [ ] (square brackets): list
• { } (curly brackets): set (or dict)
• ( ) (parentheses): tuple

type([1, 2, 3])

list

type({1, 2, 3})

set

type({1: "one", 2: "two", 3: "three"})

dict

type((1, 2, 3))

tuple

3. Python Libraries

(From most basic to most fancy)

1. NumPy: import numpy as np

$\rightarrow$ Math with arrays

2. Pandas: import pandas as pd

$\rightarrow$ Math with Tables (DataFrames)

3. Matplotlib: import matplotlib.pyplot as plt

$\rightarrow$ Visualizing NumPy/Pandas objects

4. Statsmodels: import statsmodels.formula.api as smf

$\rightarrow$ Statistical hypothesis testing

5. Seaborn: import seaborn as sns

$\rightarrow$ Visualizing statistical hypothesis tests

6. Scikit-learn: import sklearn

$\rightarrow$ Fancy machine learning things

NumPy

import numpy as np
cool_array = np.array([1, 2, 3, 4, 5])
cool_array.std()

1.4142135623730951

Pandas

import pandas as pd
cool_df = pd.DataFrame(
    {'x':[1,2,3,4,5,6,7,8],
     'y':[2,4,5,5,7,9,10,13],
     'z':[0,0,1,0,1,1,1,1]}
)
cool_df.head()

	x	y	z
0	1	2	0
1	2	4	0
2	3	5	1
3	4	5	0
4	5	7	1

Matplotlib

import matplotlib.pyplot as plt
plt.scatter(cool_df['x'], cool_df['y'])
plt.show()

Statsmodels

import statsmodels.formula.api as smf
result = smf.ols('y ~ x', data=cool_df).fit()
print(result.summary().tables[1])

==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
Intercept      0.3929      0.614      0.640      0.546      -1.110       1.895
x              1.4405      0.122     11.846      0.000       1.143       1.738
==============================================================================

Seaborn

import seaborn as sns
sns.regplot(x='x', y='y', data=cool_df);

Scikit-learn

import sklearn

import scikitplot as skplt
skplt.metrics.plot_confusion_matrix(classes, predictions, normalize=True)
plt.show()