Week 8: Propensity Score Weighting
DSAN 5650: Causal Inference for Computational Social Science
Summer 2025, Georgetown University
Wednesday, July 9, 2025
Schedule
Today’s Planned Schedule:
| Start | End | Topic | |
|---|---|---|---|
| Lecture | 6:30pm | 7:00pm | Final Project Pep Talk → |
| 7:00pm | 7:50pm | Controlling For Things vs. Matching/Weighting → | |
| Break! | 7:50pm | 8:00pm | |
| 8:00pm | 9:00pm | Propensity Score Lab → |
\[ \DeclareMathOperator*{\argmax}{argmax} \DeclareMathOperator*{\argmin}{argmin} \newcommand{\bigexp}[1]{\exp\mkern-4mu\left[ #1 \right]} \newcommand{\bigexpect}[1]{\mathbb{E}\mkern-4mu \left[ #1 \right]} \newcommand{\definedas}{\overset{\small\text{def}}{=}} \newcommand{\definedalign}{\overset{\phantom{\text{defn}}}{=}} \newcommand{\eqeventual}{\overset{\text{eventually}}{=}} \newcommand{\Err}{\text{Err}} \newcommand{\expect}[1]{\mathbb{E}[#1]} \newcommand{\expectsq}[1]{\mathbb{E}^2[#1]} \newcommand{\fw}[1]{\texttt{#1}} \newcommand{\given}{\mid} \newcommand{\green}[1]{\color{green}{#1}} \newcommand{\heads}{\outcome{heads}} \newcommand{\iid}{\overset{\text{\small{iid}}}{\sim}} \newcommand{\lik}{\mathcal{L}} \newcommand{\loglik}{\ell} \DeclareMathOperator*{\maximize}{maximize} \DeclareMathOperator*{\minimize}{minimize} \newcommand{\mle}{\textsf{ML}} \newcommand{\nimplies}{\;\not\!\!\!\!\implies} \newcommand{\orange}[1]{\color{orange}{#1}} \newcommand{\outcome}[1]{\textsf{#1}} \newcommand{\param}[1]{{\color{purple} #1}} \newcommand{\pgsamplespace}{\{\green{1},\green{2},\green{3},\purp{4},\purp{5},\purp{6}\}} \newcommand{\pedge}[2]{\require{enclose}\enclose{circle}{~{#1}~} \rightarrow \; \enclose{circle}{\kern.01em {#2}~\kern.01em}} \newcommand{\pnode}[1]{\require{enclose}\enclose{circle}{\kern.1em {#1} \kern.1em}} \newcommand{\ponode}[1]{\require{enclose}\enclose{box}[background=lightgray]{{#1}}} \newcommand{\pnodesp}[1]{\require{enclose}\enclose{circle}{~{#1}~}} \newcommand{\purp}[1]{\color{purple}{#1}} \newcommand{\sign}{\text{Sign}} \newcommand{\spacecap}{\; \cap \;} \newcommand{\spacewedge}{\; \wedge \;} \newcommand{\tails}{\outcome{tails}} \newcommand{\Var}[1]{\text{Var}[#1]} \newcommand{\bigVar}[1]{\text{Var}\mkern-4mu \left[ #1 \right]} \]
Roadmap for Part 2
- \(\downarrow\) Focus on abstract concepts / terminology
- \(\uparrow\) Focus on data analysis
- (Should hopefully start to feel more like other DSAN classes!)
- (\(\Rightarrow\) Need you to take specific examples I pick and analogize them to your field(s) of interest)
Final Projects
- Notion! Then, choose a path (rough draft of paths):
- Modeling a social phenomenon with PGMs
- Taking an existing project/interest (e.g., from 5300) and pushing towards the causality asymptote
- Choose a path by Tuesday, July 15, 6:30pm EDT
Propensity Score Weighting
- HW1 matching: similarity either 1 (applied to same schools) or 0 (didn’t apply to same schools)
- Propensity scores: model quality of match
- \(\Rightarrow\) Opens up (literally) infinite possibilities between 0 and 1!
- \(\Rightarrow\) Use your unsupervised learning skills (matching via clustering)
- \(\Rightarrow\) Use your supervised learning skills (propensity scores = logistic regression coefficients!)

- \(\Rightarrow\) Use your diagnostic skills: e.g., methods for evaluating clusters / preventing overfitting
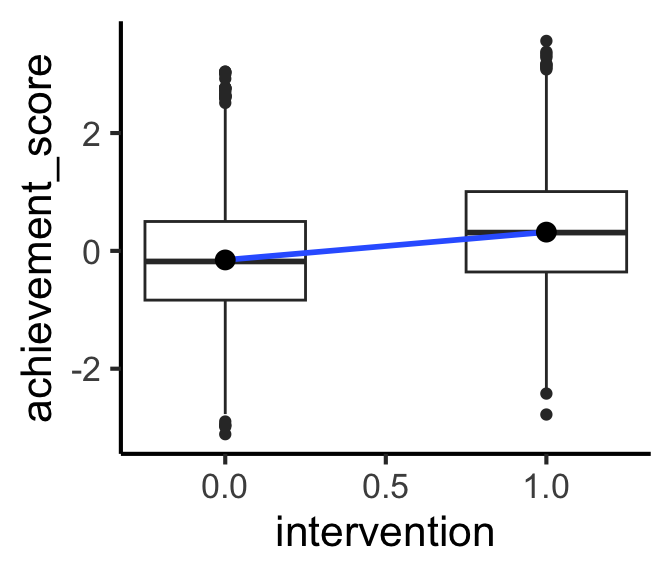
Working Example: Growth Mindset(!)
- From Athey and Wager (2019)
- Treatment \(T\), called
interventionin the dataset: a seminar on growth mindset for high school students - Outcome \(Y\), called
achievement_scorein the dataset: performance on state’s standardized test - In a perfect world, we could just compute
\[ \mathbb{E}[Y \mid T = 1] - \mathbb{E}[Y \mid T = 0] \]
Code
| intervention | mean_score |
|---|---|
| 0 | -0.1538030 |
| 1 | 0.3184686 |
Code
| term | estimate |
|---|---|
| (Intercept) | -0.1538030 |
| intervention | 0.4722717 |
Code
The Problem: Pesky Covariates
- Here the “blob” \(\mathbf{X}\) forms a fork, as drawn…
- But in reality the work of modeling is flying into the cloud and modeling the \(\mathbf{X}\)-\(T\) and \(\mathbf{X}\)-\(Y\) relationships (especially: figuring out which covariates \(X_j \in \mathbf{X}\) are colliders), so you can close the backdoors:
- This can be really difficult, for a bunch of reasons… What if there was an easier way?
If We Had Control Over Everything (Experiments vs. Observational Data Analysis)
- If we could intervene in the DGP, we could assign treatment randomly, thus removing the impact of Covariates on \(T\)!
- Alas, we are data scientists, not (necessarily) experiment-conductors, plus there are often ethical reasons to not perform experiments!
- …There’s still another approach!
Closing Backdoors the Too-Good-To-Be-True Way
- Key insight from causal thinking: Transformation of the problem from “control for all covariates” to “close all backdoor paths”…
- For the goal of just closing these paths, we have an alternative1:
- Rosenbaum and Rubin (1983): there exists a statistic \(\mathtt{e}(\mathbf{X}) = \Pr(T \mid \mathbf{X})\), the propensity score, which “captures” info in \(\textbf{X}\) relevant to \(T\) such that
- Conditioning on \(\mathtt{e}(\mathbf{X})\) closes \(\mathbf{X} \Rightarrow \mathtt{e}(\mathbf{X}) \rightarrow T\) (\(\mathtt{e}(\mathbf{X})\) is a pipe)
- This would close backdoor path \(T \leftarrow \mathtt{e}(\mathbf{X}) \Leftarrow \mathbf{X} \rightarrow Y\), leaving only direct effect \(T \rightarrow Y\)! There’s one remaining complication…
Closing Backdoors via Propensity Score Estimation
- Sadly we don’t observe true probability of being treated for all possible values of \(\mathbf{X}\)
- But, we can derive an estimate \(\hat{\mathtt{e}}(\mathbf{X})\) using our machine learning skills 😎
- We now have that \(\hat{\mathtt{e}}(\mathbf{X})\), as a proxy relative to the pipe \(\mathbf{X} \Rightarrow \mathtt{e}(\mathbf{X}) \rightarrow T\), blocks the pipe to the extent that it captures the true probability \(\mathtt{e}(\mathbf{X}) = \Pr(T \mid \mathbf{X})\)
- Backdoor Path: \(T \leftarrow \mathtt{e}(\mathbf{X}) \Leftarrow \mathbf{X} \rightarrow Y\)
- Closed in proportion to \(\left[ \text{Cor}(\hat{\mathtt{e}}(\mathbf{X}), \mathtt{e}(\mathbf{X})) \right]^2 = ❓\)
Sometimes-Helpful Thought Experiment
- Back in our basic confounding scenario:
- If there was only one covariate (\(\mathbf{X} = X\)), and it was a constant (\(\Pr(X = c) = 1\)), then all the variation in \(Y\) would be due to variation in \(T\)
- Less extreme: if person \(i\) has covariates \(\mathbf{X}_i\) and person \(j\) has covariates \(\mathbf{X}_j\), but \(\mathbf{X}_i = \mathbf{X}_j\), then variation in their outcomes is due solely to \(T\)
- Part of the logic of propensity score is that, if person \(i\) has covariates \(\mathbf{X}_i\) and person \(j\) has covariates \(\mathbf{X}_j\), but \(\mathtt{e}(\mathbf{X}_i) = \mathtt{e}(\mathbf{X}_j)\), then \(i\) and \(j\) are perfectly matched
- \(\Rightarrow\) (by fun math proof) variation in their outcomes is due solely to \(T\)
How Exactly Do We Adjust For \(\hat{\mathtt{e}}(\mathbf{X})\)?
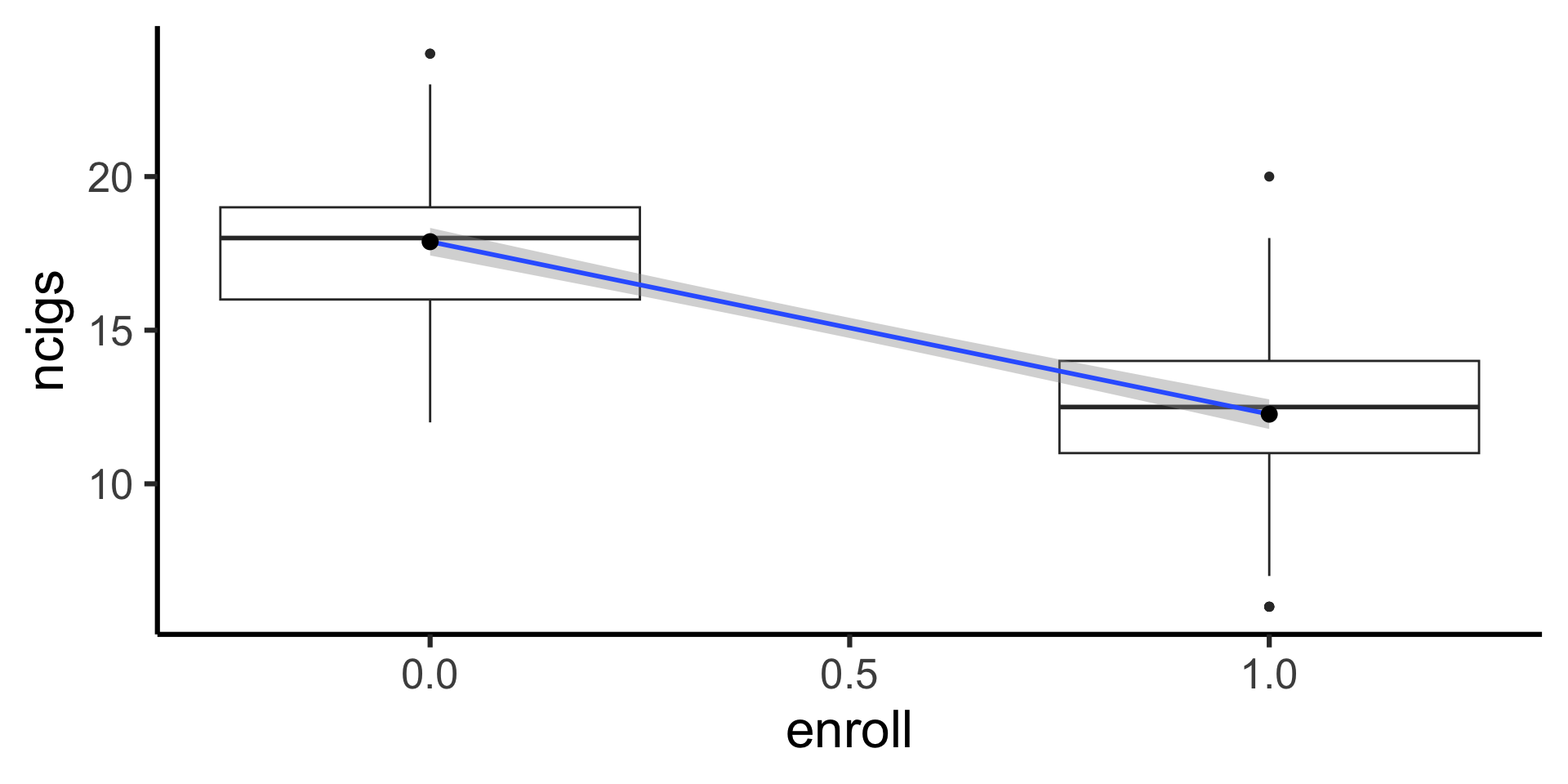
- Simulation example: smoking reduction
Code
library(tidyverse)
library(Rlab)
set.seed(5650)
n <- 250
motiv_vals <- runif(n, 0, 1)
enroll_vals <- ifelse(
motiv_vals < 0.25,
0,
# We know motiv > 0.25
ifelse(
motiv_vals > 0.75,
1,
# We know 0.25 < motiv < 0.75
rbern(n, prob=(motiv_vals - 0.125)*1.5)
)
)
ncigs_vals <- rbinom(n, size=30, prob=0.6-0.2*enroll_vals)
smoke_df <- tibble(
motiv=motiv_vals,
enroll=enroll_vals,
ncigs=ncigs_vals
)
(smoke_mean_df <- smoke_df |> group_by(enroll) |> summarize(mean_ncigs=mean(ncigs)))| enroll | mean_ncigs |
|---|---|
| 0 | 17.88060 |
| 1 | 12.26724 |
Code
| term | estimate |
|---|---|
| (Intercept) | 17.880597 |
| enroll | -5.613356 |
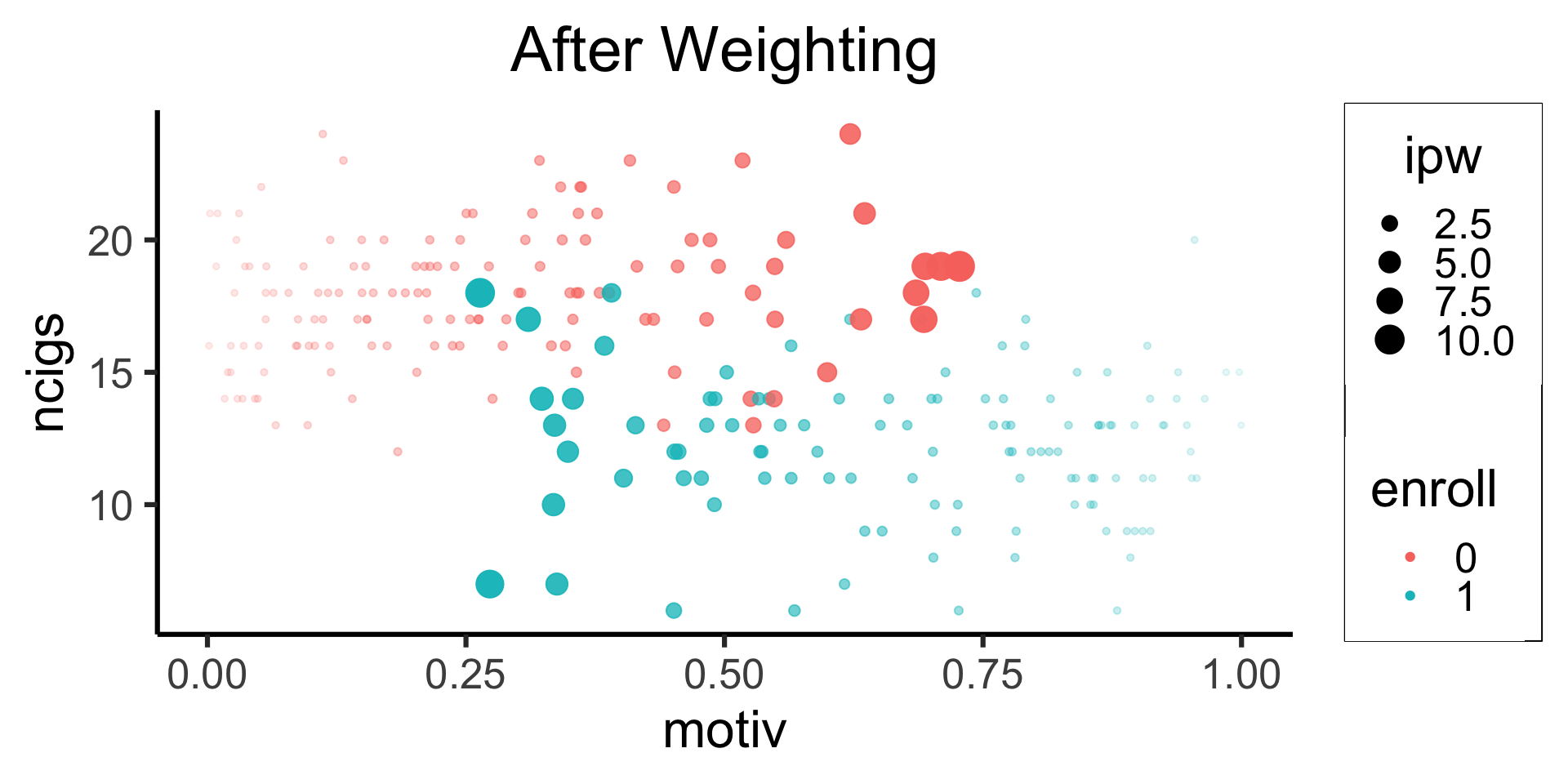
Inverse Probability-of-Treatment Weighting
Code
eprop_model <- glm(enroll ~ motiv, family='binomial', data=smoke_df)
eprop_preds <- predict(eprop_model, type="response")
smoke_df <- smoke_df |> mutate(pred=eprop_preds)
# Use the preds to compute IPW
smoke_df <- smoke_df |> rowwise() |> mutate(
ipw=ifelse(enroll, 1/pred, 1/(1-pred))
) |> arrange(pred)
#smoke_df
smoke_df |> mutate(enroll=factor(enroll)) |>
ggplot(aes(x=motiv, y=ncigs, color=enroll)) +
geom_point() +
theme_dsan(base_size=24) +
labs(title="Before Weighting")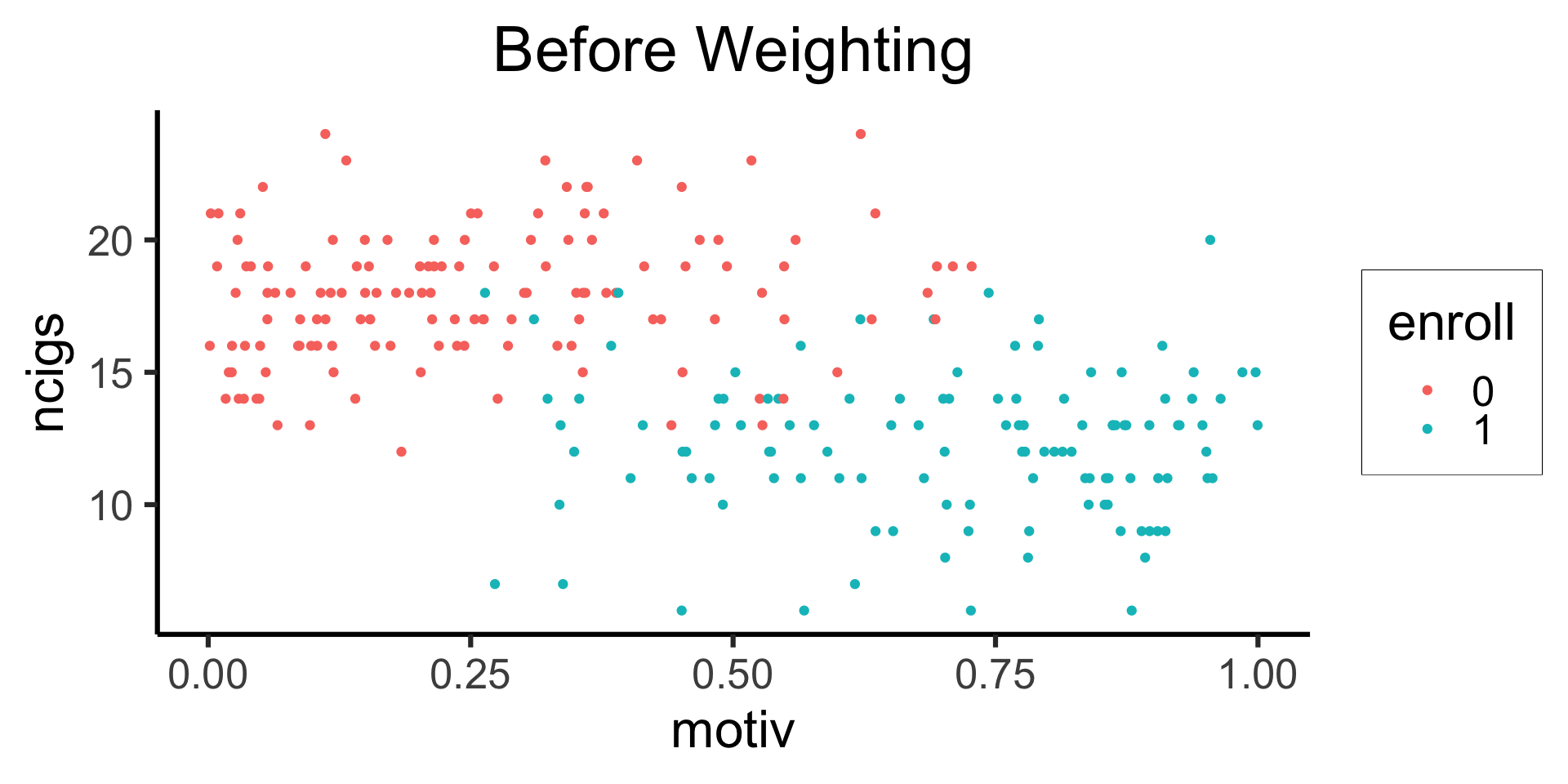
Code
smoke_df |>
ggplot(aes(x=motiv)) +
# Predictions
geom_point(
aes(y=enroll, color=factor(enroll))
) +
# Values
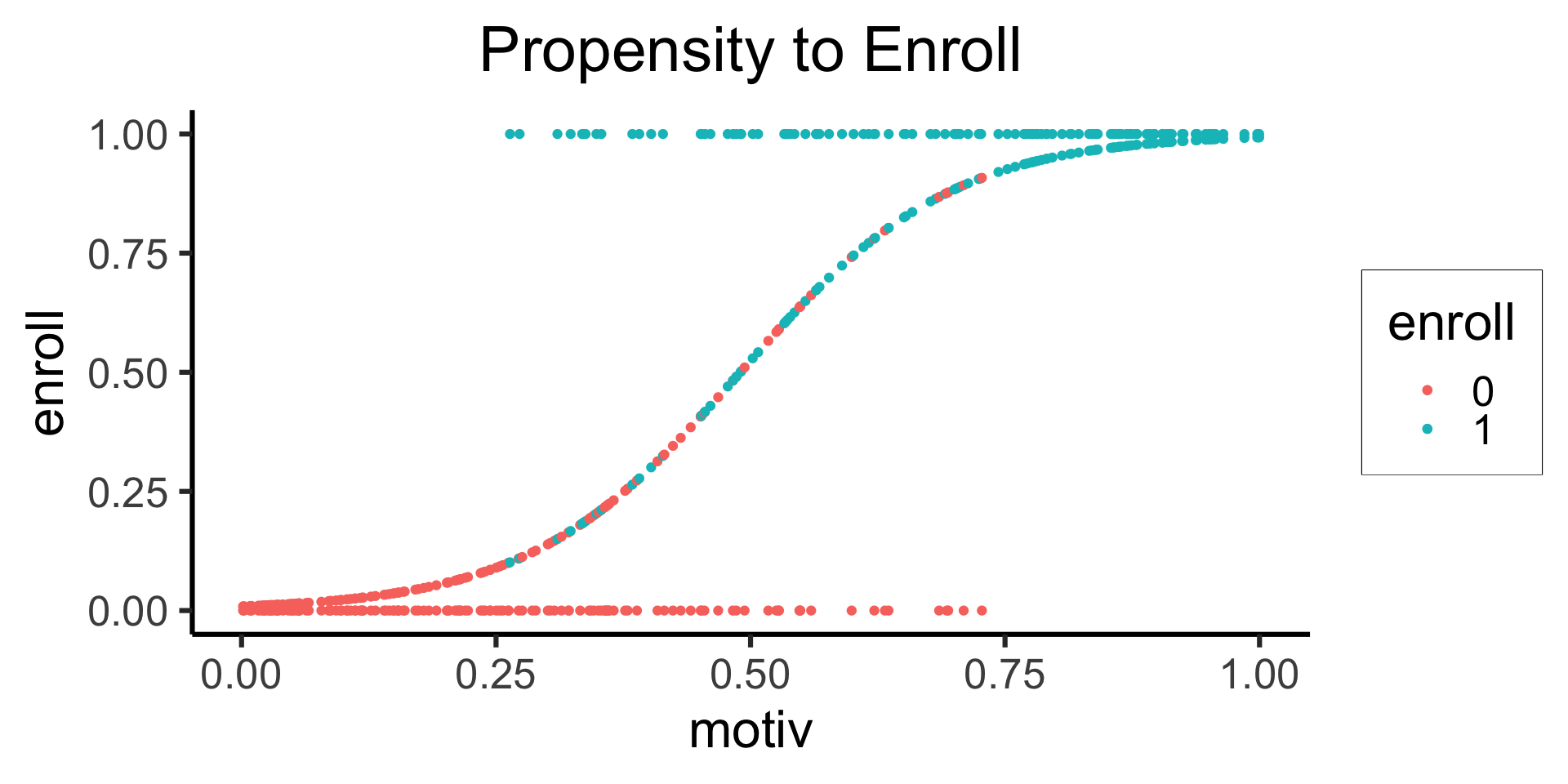
geom_point(
aes(y=pred, color=factor(enroll))
) +
labs(color="enroll") +
theme_dsan(base_size=24) +
labs(title="Propensity to Enroll")
ipw_min <- min(smoke_df$ipw)
ipw_max <- max(smoke_df$ipw)
smoke_df <- smoke_df |> mutate(
ipw_scaled = (ipw - ipw_min) / (ipw_max - ipw_min)
)
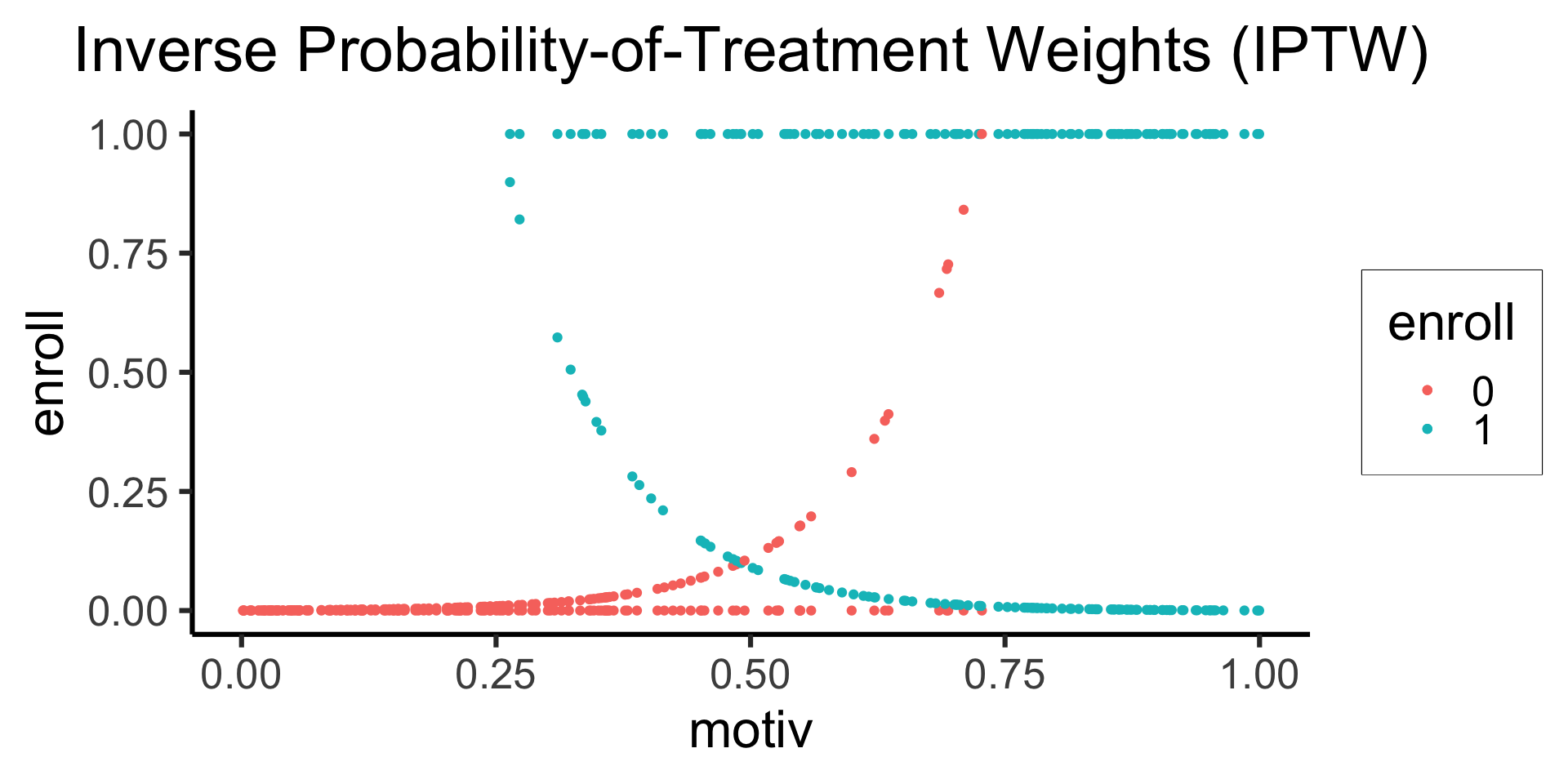
smoke_df |>
ggplot(aes(x=motiv)) +
# Predictions
geom_point(
aes(y=enroll, color=factor(enroll))
) +
# Values
geom_point(
aes(y=ipw_scaled, color=factor(enroll))
) +
theme_dsan(base_size=24) +
labs(
title="Inverse Probability-of-Treatment Weights (IPTW)",
color="enroll"
)↓
→
↑
The Final Result!
| term | estimate | std.error |
|---|---|---|
| (Intercept) | 18.10133 | 0.2466712 |
| enroll | -5.66453 | 0.3571696 |
Call:
lm_weightit(formula = ncigs ~ enroll, data = smoke_df, weightit = W)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 18.1013 0.2479 73.02 <1e-06 ***
enroll -5.6645 0.5463 -10.37 <1e-06 ***
Standard error: HC0 robust
Call:
lm_weightit(formula = ncigs ~ enroll, data = smoke_df, weightit = W_default)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 18.1013 0.2441 74.16 <1e-06 ***
enroll -5.6645 0.5444 -10.41 <1e-06 ***
Standard error: HC0 robust (adjusted for estimation of weights)…What If We Have Many Covariates?
- Curse of dimensionality…
- Lab Time!
References
DSAN 5650 Week 8: Propensity Score Weighting