Week 3: From PGMs to Causal Diagrams

DSAN 5650: Causal Inference for Computational Social Science
Summer 2025, Georgetown University

Jeff Jacobs

jj1088@georgetown.edu

Wednesday, June 4, 2025

Schedule

Today’s Planned Schedule:

	Start	End	Topic
Lecture	6:30pm	6:45pm	HW1 Questions and Concerns →
	6:45pm	7:15pm	Causality Recap →
	7:00pm	7:30pm	Motivating Examples: Causal Inference →
	7:30pm	7:45pm	Your First Probabilistic Graphical Model! →
Break!	7:45pm	8:00pm
	8:00pm	9:00pm	PGM “Lab” →

cb_palette = [
    "#E69F00", "#56B4E9", "#009E73",
    "#F0E442", "#0072B2", "#D55E00",
    "#CC79A7"
]

\[ \DeclareMathOperator*{\argmax}{argmax} \DeclareMathOperator*{\argmin}{argmin} \newcommand{\bigexp}[1]{\exp\mkern-4mu\left[ #1 \right]} \newcommand{\bigexpect}[1]{\mathbb{E}\mkern-4mu \left[ #1 \right]} \newcommand{\definedas}{\overset{\small\text{def}}{=}} \newcommand{\definedalign}{\overset{\phantom{\text{defn}}}{=}} \newcommand{\eqeventual}{\overset{\text{eventually}}{=}} \newcommand{\Err}{\text{Err}} \newcommand{\expect}[1]{\mathbb{E}[#1]} \newcommand{\expectsq}[1]{\mathbb{E}^2[#1]} \newcommand{\fw}[1]{\texttt{#1}} \newcommand{\given}{\mid} \newcommand{\green}[1]{\color{green}{#1}} \newcommand{\heads}{\outcome{heads}} \newcommand{\iid}{\overset{\text{\small{iid}}}{\sim}} \newcommand{\lik}{\mathcal{L}} \newcommand{\loglik}{\ell} \DeclareMathOperator*{\maximize}{maximize} \DeclareMathOperator*{\minimize}{minimize} \newcommand{\mle}{\textsf{ML}} \newcommand{\nimplies}{\;\not\!\!\!\!\implies} \newcommand{\orange}[1]{\color{orange}{#1}} \newcommand{\outcome}[1]{\textsf{#1}} \newcommand{\param}[1]{{\color{purple} #1}} \newcommand{\pgsamplespace}{\{\green{1},\green{2},\green{3},\purp{4},\purp{5},\purp{6}\}} \newcommand{\pedge}[2]{\require{enclose}\enclose{circle}{~{#1}~} \rightarrow \; \enclose{circle}{\kern.01em {#2}~\kern.01em}} \newcommand{\pnode}[1]{\require{enclose}\enclose{circle}{~{#1}~}} \newcommand{\purp}[1]{\color{purple}{#1}} \newcommand{\sign}{\text{Sign}} \newcommand{\spacecap}{\; \cap \;} \newcommand{\spacewedge}{\; \wedge \;} \newcommand{\tails}{\outcome{tails}} \newcommand{\Var}[1]{\text{Var}[#1]} \newcommand{\bigVar}[1]{\text{Var}\mkern-4mu \left[ #1 \right]} \]

HW1 Questions and/or Concerns

• 🆕 Submitting to AutoHinter! 🆕

Causality Recap

So What’s the Problem?

• Non-probabilistic models: High potential for being garbage
  • tldr: even if SUPER certain, using \(\Pr(\mathcal{H}) = 1-\varepsilon\) with tiny \(\varepsilon\) has literal life-saving advantages¹ (Finetti 1972)
• Probabilistic models: Getting there, still looking at “surface”
  • Of the \(N = 100\) times we observed event \(X\) occurring, event \(Y\) also occurred \(90\) of those times
  • \(\implies \Pr(Y \mid X) = \frac{\#[X, Y]}{\#[X]} = \frac{90}{100} = 0.9\)
• Causal models: Does \(Y\) happen because of \(X\) happening? For that, need to start modeling what’s happening under the surface making \(X\) and \(Y\) “pop up” together so often

1. See Appendix Slide

The Fundamental Problem of Causal Inference

The only workable definition of «\(X\) causes \(Y\)»:

Defining Causality (Hume 1739, ruining everything as usual 😤)

\(X\) causes \(Y\) if and only if:

1. \(X\) temporally precedes \(Y\) and
2. • In two worlds \(W_0\) and \(W_1\) where
   • everything is exactly the same except that \(X = 0\) in \(W_0\) and \(X = 1\) in \(W_1\),
   • \(Y = 0\) in \(W_0\) and \(Y = 1\) in \(W_1\)

• The problem? We live in one world, not two identical worlds simultaneously 😭

What Is To Be Done?

Probability++

• Tools from prob/stats (RVs, CDFs, Conditional Probability) necessary but not sufficient for causal inference!
• Example: Say we use DSAN 5100 tools to discover:
  • Probability that event \(E_1\) occurs is \(\Pr(E_1) = 0.5\)
  • Probability that \(E_1\) occurs conditional on another event \(E_0\) occurring is \(\Pr(E_1 \mid E_0) = 0.75\)
• Unfortunately, we still cannot infer that the occurrence of \(E_0\) causes an increase in the likelihood of \(E_1\) occurring.

Beyond Conditional Probability

• This issue (that conditional probabilities could not be interpreted causally) at first represented a kind of dead end for scientists interested in employing probability theory to study causal relationships…
• Recent decades: researchers have built up an additional “layer” of modeling tools, augmenting existing machinery of probability to address causality head-on!
• Pearl (2000): Formal proofs that (\(\Pr\) axioms) \(\cup\) (\(\textsf{do}\) axioms) \(\Rightarrow\) causal inference procedures successfully recover causal effects

Preview: do-Calculus

• Extends core of probability to incorporate causality, via \(\textsf{do}\) operator
• \(\textsf{do}(X = 5)\) is a “special” event, representing intervention in DGP to force \(X \leftarrow 5\)… \(\textsf{do}(X = 5)\) not the same event as \(X = 5\)!

\(X = 5\)	\(\neq\)	\(\textsf{do}(X = 5)\)
Observing that \(X\) took on value 5 (for some possibly-unknown reason)	\(\neq\)	Intervening to force \(X \leftarrow 5\), all else in DGP remaining the same (intervention then “flows” through rest of DGP)

• Probably the most difficult thing in 5650 to wrap head around

• “Special”: \(\Pr(\textsf{do}(X = 5))\) not well-defined, only \(\Pr(Y = 6 \mid \textsf{do}(X = 5))\)

• To emphasize special-ness, we may use notation like:

  \[ \Pr(Y = 6 \mid \textsf{do}(X = 5)) \equiv \textstyle \Pr_{\textsf{do}(X = 5)}(Y = 6) \]

  to avoid confusion with “normal” events

Causal World Unlocked 😎 (With Great Power Comes Great Responsibility…)

• With \(\textsf{do}(\cdot)\) in hand… (Alongside DGP satisfying axioms slightly more strict than core probability axioms)
• We can make causal inferences from similar pair of facts! If:
  • Probability that event \(E_1\) occurs is \(\Pr(E_1) = 0.5\),
  • The probability that \(E_1\) occurs conditional on the event \(\textsf{do}(E_0)\) occurring is \(\Pr(E_1 \mid \textsf{do}(E_0)) = 0.75\),
• Now we can actually infer that the occurrence of \(E_0\) caused an increase in the likelihood of \(E_1\) occurring!

Back to PGMs: Case Studies

Importance of Observed vs. Latent Distinction!

• Across many different fields, hidden stumbling-block in your project may be failure to model this distinction and pursue its implications!

Figure 1: Your model failing to achieve its goal bc you haven’t yet distinguished observed vs. latent variables

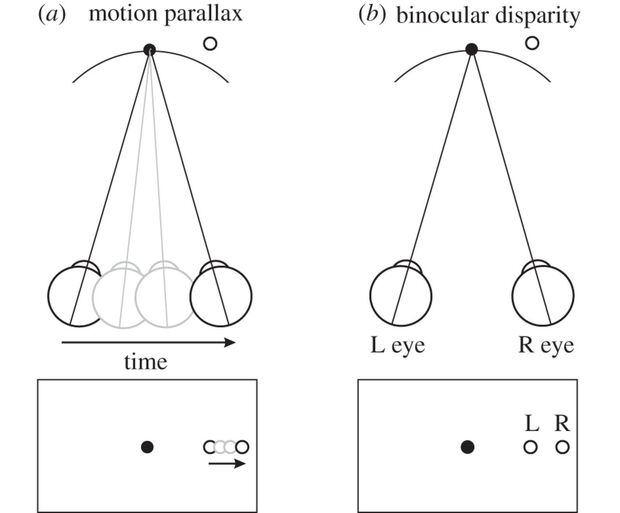
Example from Cognitive Neuroscience: Visual Perception

• We “see” 3D objects like a basketballs, but our eyes are (curved) 2D surfaces!
• \(\Rightarrow\) Our brains construct 3D environment by combining 2D info (observed photons-hitting-light-cones) with latent heuristic info:
  • Instantaneous Binocular Disparity, fusing info from two slightly-offset eyes,
  • Short-term Motion Parallax: How does object shift over short temporal “windows” of movement?
  • Long-term mental models (orange-ish circle with this line pattern is usually a basketball, which is usually this big, etc.)

Image source (a very cool article!)

• Similar examples in many other fields \(\leadsto\) science is a strange waltz of general models vs. field-specific details, but there’s one model that is infinitely helpful imo…

Hidden Markov Models (HMMs) Are Our Ur-PGMs!

• Using “Ur” in the same sense as “America’s Ur-Choropleths”…
• HMMs are our “Ur-Models” for Computational Social Science specifically

• Let’s consider an extremely currently-popular strand of CSS research, and step through why (a) it may be harder than it initially seems, but (b) we can use HMMs to “organize”/manage/visualize the complexity!

As in, how America’s Ur-Choropleths are two visualizations you can keep at hand before launching into a specific nation-wide choropleth about a specific issue!

Studying “Fake News”

Studying “fake news” with ML and/or Deep Learning and/or Big Data is very popular in Computational Social Science: let’s use HMMs to see why it might be more… difficult/complicated than it seems at first 🙈

• The (implicit) model in studies like Iyengar and Kinder (2010) is something like:

• Thus allowing results to be summarized in a table like:

Iyengar and Kinder (2010)

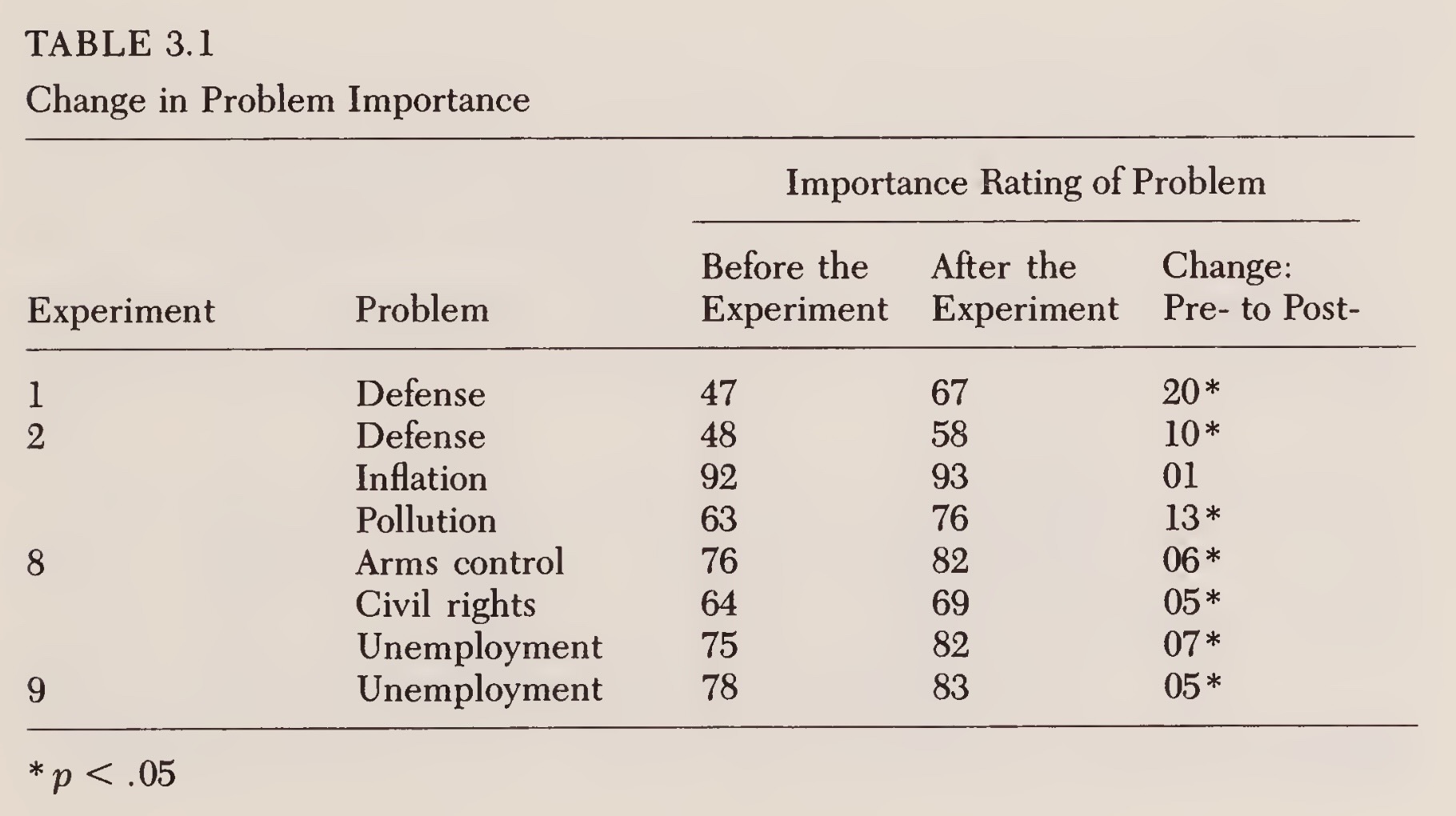
The Devil in the Details I

Residents of the New Haven, Connecticut area participated in one of two experiments, each of which spanned six consecutive days […] took place in November 1980, shortly after the presidential election

We measured problem importance with four questions that appeared in both the pretreatment and posttreatment questionnaires:

• Please indicate how important you consider these problems to be.
• Should the federal government do more to develop solutions to these problems, even if it means raising taxes?
• How much do you yourself care about these problems?
• These days how much do you talk about these problems?

The Devil in the Details II

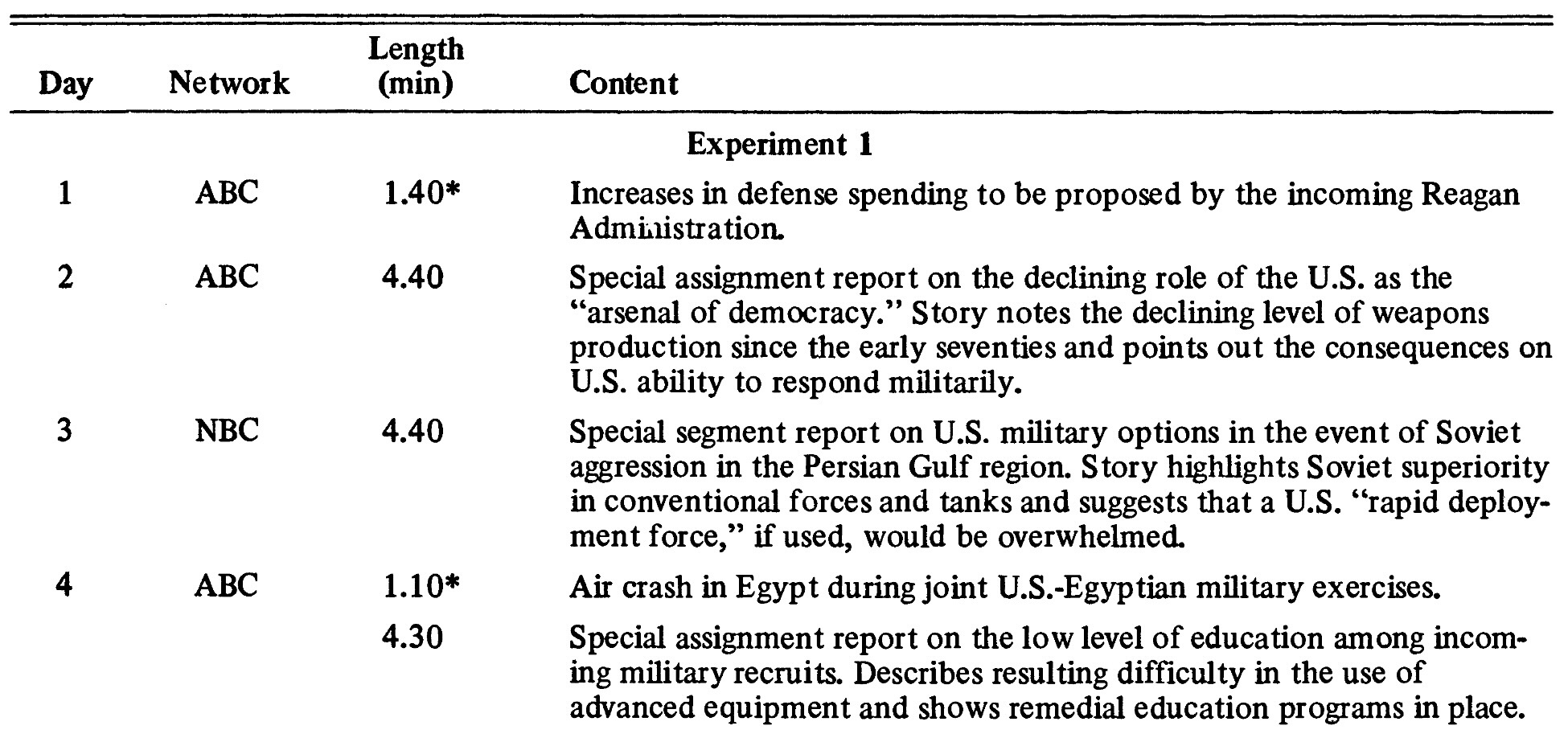
Randomization and Fine-Tuned Treatment

• …These are the types of things we usually don’t have control over as data scientists (we’re just handed a .csv!)

Let’s Model It!

The Final Piece: Plate Notation

• For describing general distributions, there is often a “single node generating a bunch of nodes” structure:

• PGM notation has a built-in tool for this: plates!

Crucial CSS Model We Can Now Dive Into!

Image source

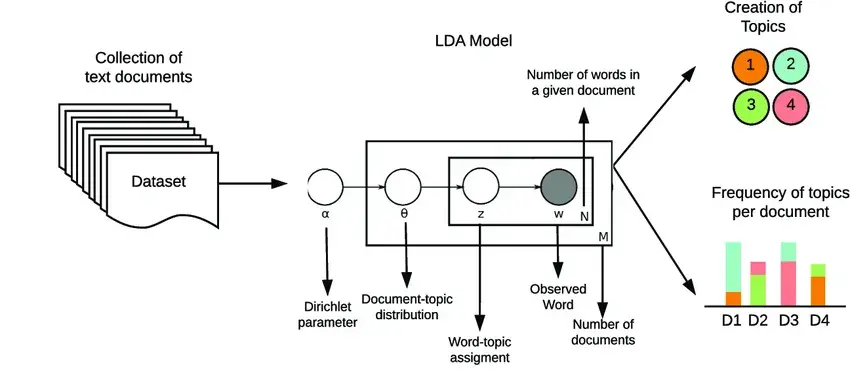
What Does This Give Us?

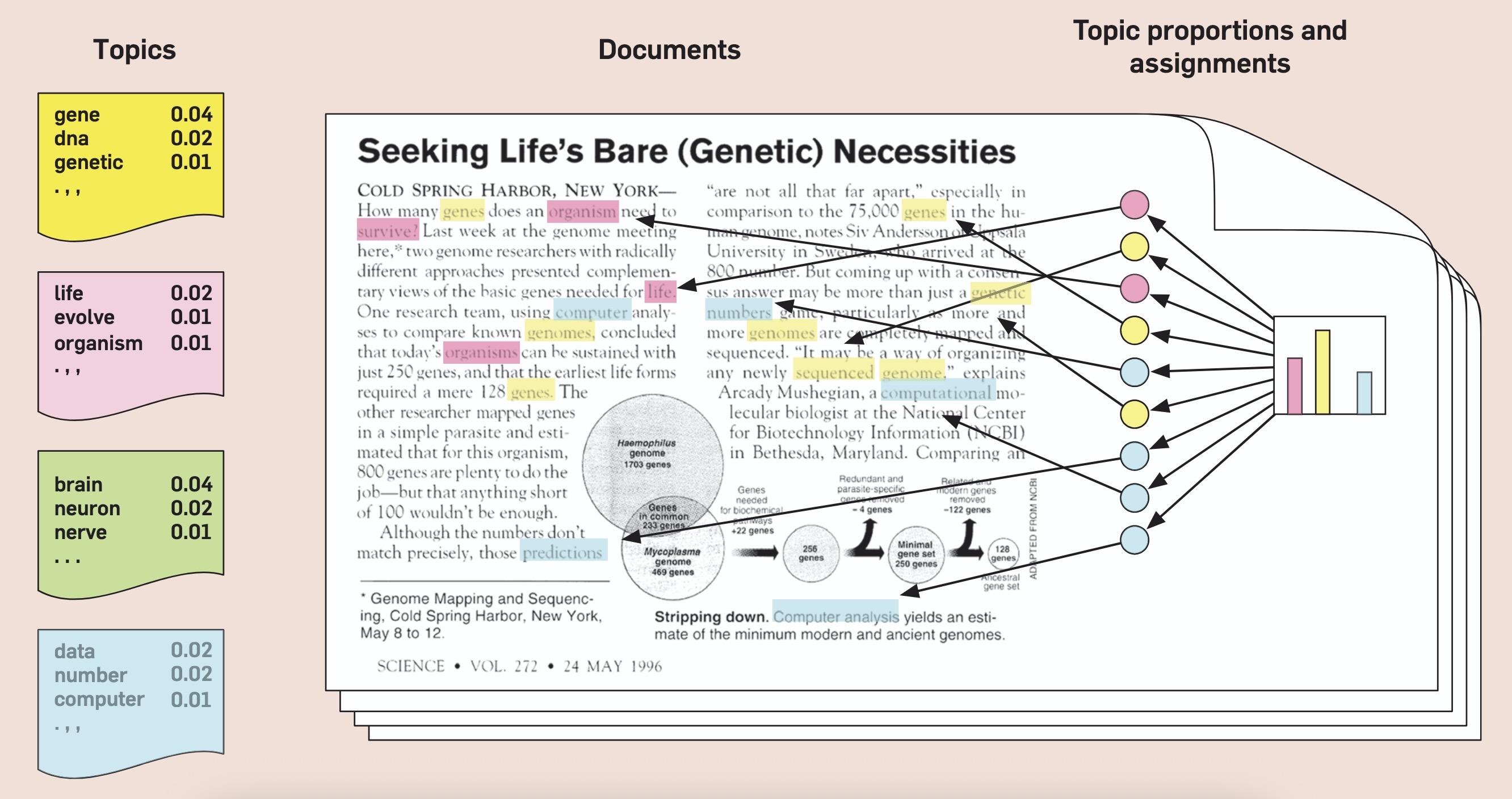
Before We Branch Off Of PGMs

(Even in non-causal settings)

Image source

• We don’t exactly think “Shakespeare decided on a set of topics,”

Your First Causal Diagram

Getting Shot By A Firing Squad

\(O\)	\(C\)	\(A\)	\(B\)	\(D\)
0	0	0	0	0
1	1	1	1	1
0	0	0	0	0
0	0	0	0	0
1	1	1	1	1

\[ \begin{align*} \Pr(D) &= 0.4 \\ \Pr(D \mid A) &= 1 \end{align*} \]

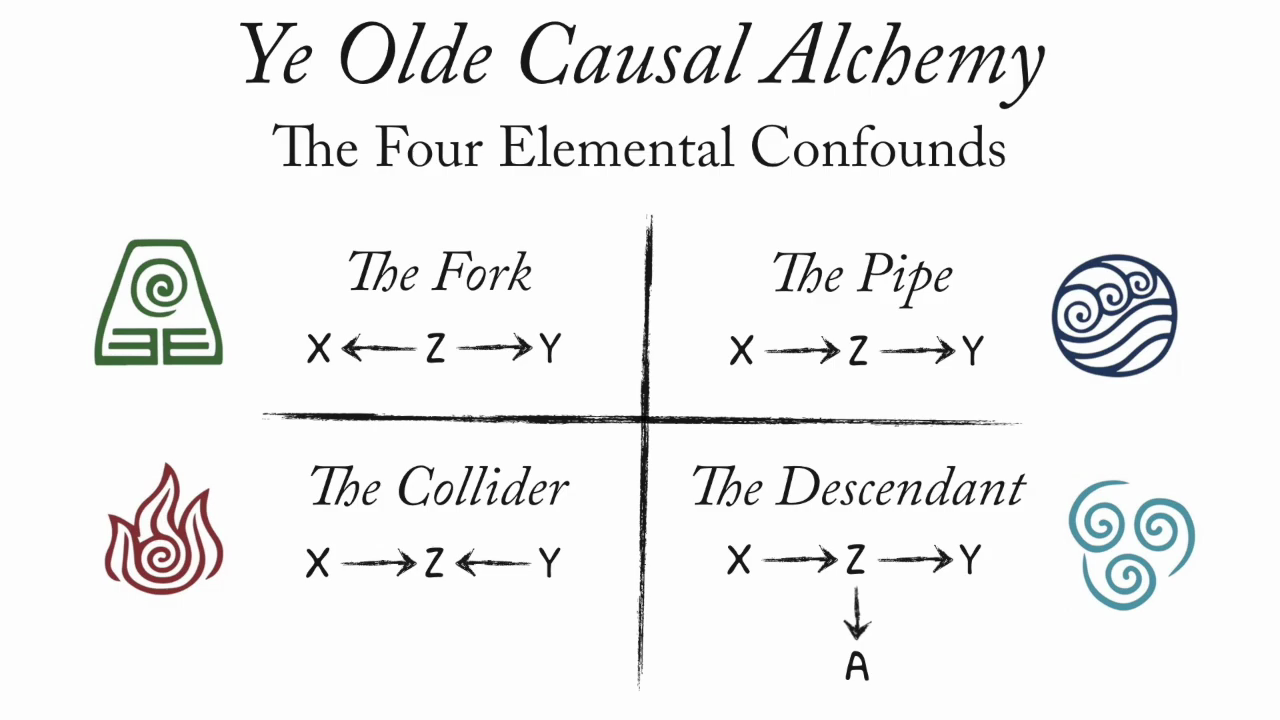
The Four Elemental Confounds

References

Finetti, Bruno de. 1972. Probability, Induction and Statistics: The Art of Guessing. J. Wiley.

Hume, David. 1739. A Treatise of Human Nature: Being an Attempt to Introduce the Experimental Method of Reasoning Into Moral Subjects; and Dialogues Concerning Natural Religion. Longmans, Green.

Iyengar, Shanto, and Donald R. Kinder. 2010. News That Matters: Television & American Opinion. University of Chicago Press.

Pearl, Judea. 2000. Causality: Models, Reasoning, and Inference. Cambridge University Press. https://www.dropbox.com/scl/fi/4kfpro4gpx7tg55fwd7qt/Judea-Pearl-Causality_-Models-Reasoning-and-Inference.pdf?rlkey=f0abw0cgmsyiegx6xapq5z7j2&dl=1.