Week 2: Software Design Patterns and Object-Oriented Programming

DSAN 5500: Data Structures, Objects, and Algorithms in Python

Jeff Jacobs

jj1088@georgetown.edu

Thursday, January 15, 2026

Where We Left Off: Primitive Types

None

\[ \underset{\text{\small{Always 0}}}{\underline{\hspace{16mm}}} \]

Code 
x = None
type(x)
NoneType

Boolean (True or False)

\[ \underset{\{0,1\}}{\underline{\hspace{12mm}}} \]

Code 
x = True
type(x)
bool

Numbers (int, float)

\[ \small{\underset{\small{\{0,1\}}}{\underline{\hspace{8mm}}}~ \underset{\small{\{0,1\}}}{\underline{\hspace{8mm}}}~ \underset{\small{\{0,1\}}}{\underline{\hspace{8mm}}}~ \underset{\small{\{0,1\}}}{\underline{\hspace{8mm}}}~ \underset{\small{\{0,1\}}}{\underline{\hspace{8mm}}}~ \underset{\small{\{0,1\}}}{\underline{\hspace{8mm}}}~ \underset{\small{\{0,1\}}}{\underline{\hspace{8mm}}}~ \underset{\small{\{0,1\}}}{\underline{\hspace{8mm}}}} \]

Code 
x = 3
print(type(x))
y = 3.14
type(y)
<class 'int'>
float
  • Why do we distinguish these from all other types? Computer knows in advance how much space they’ll take up! (None: 1 bit, bool: 1 bit, int: 32/64 bits)

Primitive Types: Python Weirdness Edition

None: 1 bit (Always 0)

import sys
sys.getsizeof(None)
16

Boolean (True or False): Exactly 1 bit (0 or 1)

sys.getsizeof(True)
28

int: 32 or 64 bits (depending on OS)

sys.maxsize
9223372036854775807

Why is this happening?

Stack and Heap in C / Java

my_beautiful_app.c
time_t current_time = time(NULL);
int num_rows = 13;
bool filled = true;
bool empty = false;
int num_cols = 2;
char username[] = "Jeff";
int i = 0;
int j = None;
void z = NULL;

Stack and Heap in Python

my_beautiful_app.py
import datetime
cur_date = datetime.datetime.now()
num_rows = 13
filled = True
empty = False
num_cols = 2
username = "Jeff"
i = 0
j = None
z = 314

Side-by-Side

Algorithmic Thinking

  • What are the inputs?
  • What are the outputs?
  • Standard cases vs. corner cases
  • Adversarial development: brainstorm all of the ways an evil hacker might break your code!

Example: Finding An Item Within A List

  • Seems straightforward, right? Given a list l, and a value v, return the index of l which contains v
  • Corner cases galore…
  • What if l contains v more than once? What if it doesn’t contain v at all? What if l is None? What if v is None? What if l isn’t a list at all? What if v is itself a list?

Corner Cases

  • Most people stand in the center of a room…
  • Eccentric weirdos stand in the corner
  • Your algorithm needs to handle all people

Demo

Streamlit Dictionary Lookup Demo

Data Structures: Motivation

Why Does NYC Subway Have Express Lines?

From NYC Central Park website

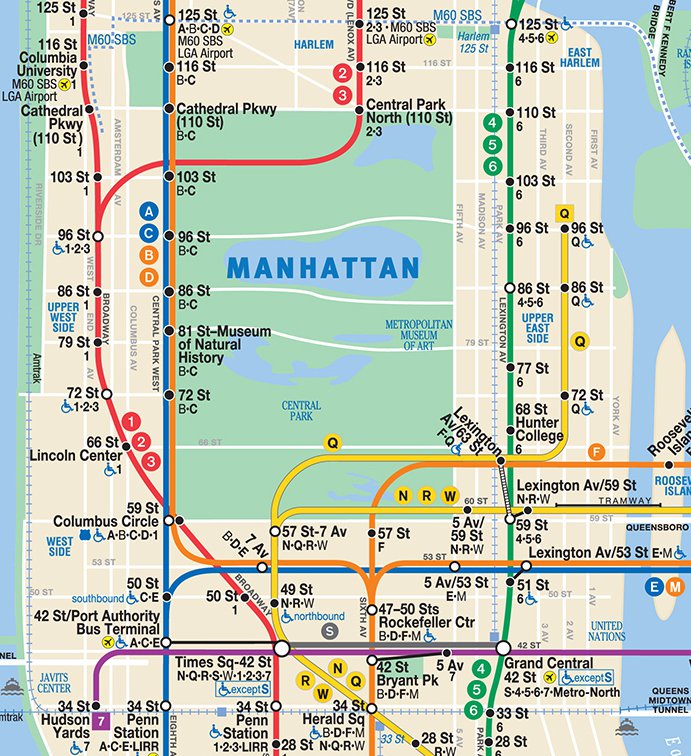
Why Stop At Two Levels?

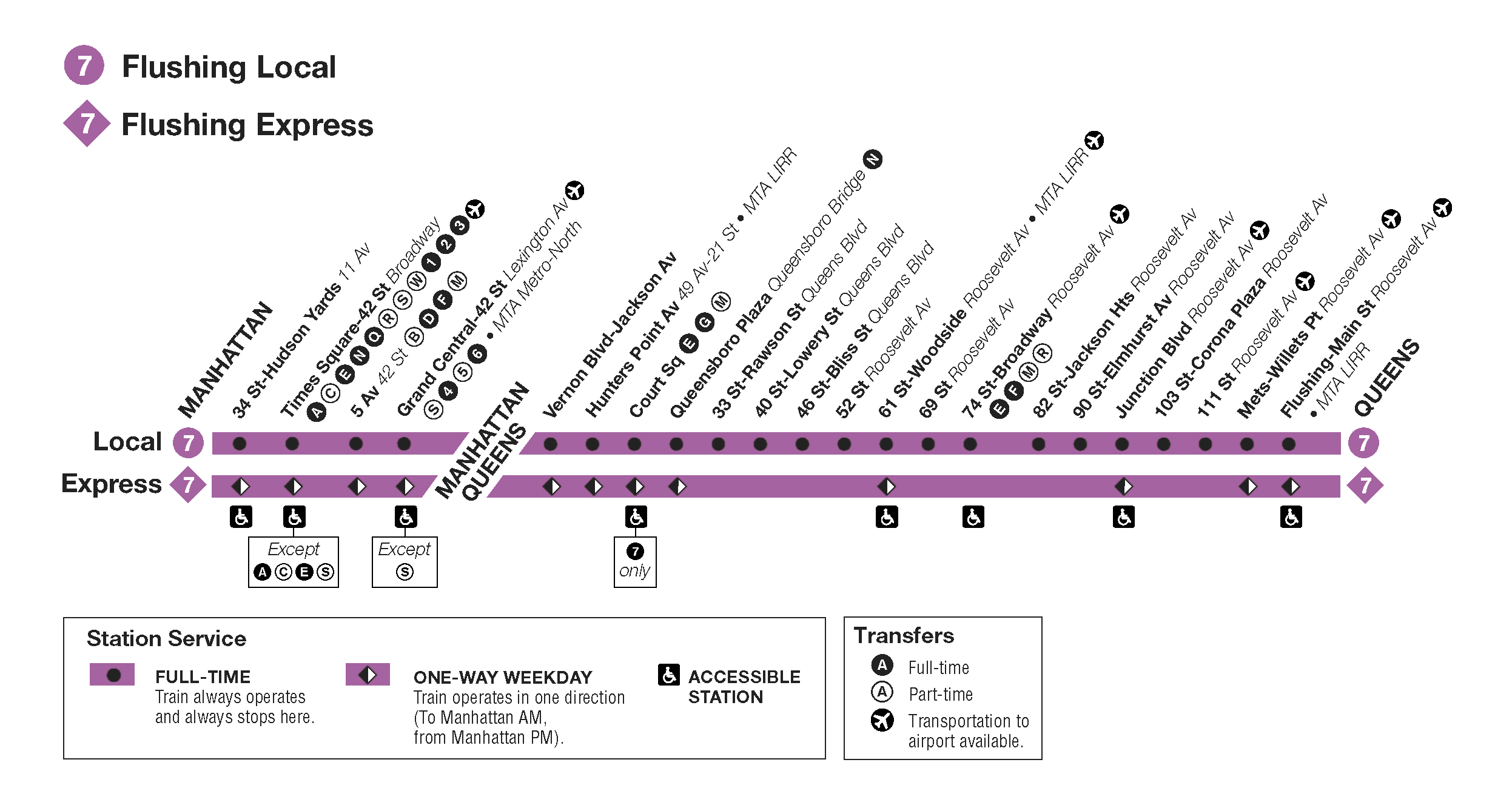
From Skip List Data Structure Explained, Sumit’s Diary blog

How TF Does Google Maps Work?

  • A (mostly) full-on answer: soon to come! Data structures for spatial data
  • A step in that direction: Quadtrees! (Fractal DC)

Jim Kang’s Quadtree Visualizations

Algorithmic Complexity: Motivation

The Secretly Exciting World of Matrix Multiplication

  • Fun Fact 1: Most of modern Machine Learning is, at the processor level, just a bunch of matrix operations
  • Fun Fact 2: The way we’ve all learned how to multiply matrices requires \(O(N^3)\) operations, for two \(N \times N\) matrices \(A\) and \(B\)
  • Fun Fact 3: \(\underbrace{x^2 - y^2}_{\mathclap{\times\text{ twice, }\pm\text{ once}}} = \underbrace{(x+y)(x-y)}_{\times\text{once, }\pm\text{ twice}}\)
  • Fun Fact 4: These are not very fun facts at all

Why Is Jeff Rambling About Matrix Math From 300 Years Ago?

  • The way we all learned it in school (for \(N = 2\)):

\[ AB = \begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{bmatrix} \begin{bmatrix} b_{11} & b_{12} \\ b_{21} & b_{22} \end{bmatrix} = \begin{bmatrix} a_{11}b_{11} + a_{12}b_{21} & a_{11}b_{12} + a_{12}b_{22} \\ a_{21}b_{11} + a_{22}b_{21} & a_{21}b_{12} + a_{22}b_{22} \end{bmatrix} \]

  • 12 operations: 8 multiplications, 4 additions \(\implies O(N^3) = O(2^3) = O(8)\)
  • Are we trapped? Like… what is there to do besides performing these \(N^3\) operations, if we want to multiply two \(N \times N\) matrices? Why are we about to move onto yet another slide about this?

Block-Partitioning Matrices

  • Now let’s consider big matrices, whose dimensions are a power of 2 (for ease of illustration): \(A\) and \(B\) are now \(N \times N = 2^n \times 2^n\) matrices
  • We can “decompose” the matrix product \(AB\) as:

\[ AB = \begin{bmatrix} A_{11} & A_{12} \\ A_{21} & A_{22} \end{bmatrix} \begin{bmatrix} B_{11} & B_{12} \\ B_{21} & B_{22} \end{bmatrix} = \begin{bmatrix} A_{11}B_{11} + A_{12}B_{21} & A_{11}B_{12} + A_{12}B_{22} \\ A_{21}B_{11} + A_{22}B_{21} & A_{21}B_{12} + A_{22}B_{22} \end{bmatrix} \]

  • Which gives us a recurrence relation representing the total number of computations required for this big-matrix multiplication: \(T(N) = \underbrace{8T(N/2)}_{\text{Multiplications}} + \underbrace{\Theta(1)}_{\text{Additions}}\)
  • It turns out that (using a method we’ll learn in Week 3), given this recurrence relation and our base case from the previous slide, this divide-and-conquer approach via block-partitioning doesn’t help us: we still get \(T(n) = O(n^3)\)…
  • So why is Jeff still torturing us with this example?

Time For Some 🪄MATRIX MAGIC!🪄

  • If we define

\[ \begin{align*} m_1 &= (a_{11}+a_{22})(b_{11}+b_{22}) \\ m_2 &= (a_{21}+a_{22})b_{11} \\ m_3 &= a_{11}(b_{12}-b_{22}) \\ m_4 &= a_{22}(b_{21}-b_{11}) \\ m_5 &= (a_{11}+a_{12})b_{22} \\ m_6 &= (a_{21}-a_{11})(b_{11}+b_{12}) \\ m_7 &= (a_{12}-a_{22})(b_{21}+b_{22}) \end{align*} \]

  • Then we can combine these seven scalar products to obtain our matrix product:

\[ AB = \begin{bmatrix} m_1 + m_4 - m_5 + m_7 & m_3 + m_5 \\ m_2 + m_4 & m_1 - m_2 + m_3 + m_6 \end{bmatrix} \]

  • Total operations: 7 multiplications, 18 additions

Block-Partitioned Matrix Magic

  • Using the previous slide as our base case and applying this same method to the block-paritioned big matrices, we get the same result, but where the four entries in \(AB\) here are now matrices rather than scalars:

\[ AB = \begin{bmatrix} M_1 + M_4 - M_5 + M_7 & M_3 + M_5 \\ M_2 + M_4 & M_1 - M_2 + M_3 + M_6 \end{bmatrix} \]

  • We now have a different recurrence relation: \(T(N) = \underbrace{7T(N/2)}_{\text{Multiplications}} + \underbrace{\Theta(N^2)}_{\text{Additions}}\)
  • And it turns out, somewhat miraculously, that the additional time required for the increased number of additions is significantly less than the time savings we obtain by doing 7 instead of 8 multiplications, since this method now runs in \(T(N) = O(N^{\log_2(7)}) \approx O(N^{2.807}) < O(N^3)\) 🤯