Week 1: Introduction to the Course

DSAN 5450: Data Ethics and Policy
Spring 2026, Georgetown University

Jeff Jacobs

jj1088@georgetown.edu

Wednesday, January 14, 2026

Who Am I? Why Is Georgetown Having Me Teach This?

\DeclareMathOperator*{\argmax}{argmax} \DeclareMathOperator*{\argmin}{argmin} \newcommand{\bigexp}[1]{\exp\mkern-4mu\left[ #1 \right]} \newcommand{\bigexpect}[1]{\mathbb{E}\mkern-4mu \left[ #1 \right]} \newcommand{\definedas}{\overset{\small\text{def}}{=}} \newcommand{\definedalign}{\overset{\phantom{\text{defn}}}{=}} \newcommand{\eqeventual}{\overset{\text{eventually}}{=}} \newcommand{\Err}{\text{Err}} \newcommand{\expect}[1]{\mathbb{E}[#1]} \newcommand{\expectsq}[1]{\mathbb{E}^2[#1]} \newcommand{\fw}[1]{\texttt{#1}} \newcommand{\given}{\mid} \newcommand{\green}[1]{\color{green}{#1}} \newcommand{\heads}{\outcome{heads}} \newcommand{\iid}{\overset{\text{\small{iid}}}{\sim}} \newcommand{\lik}{\mathcal{L}} \newcommand{\loglik}{\ell} \DeclareMathOperator*{\maximize}{maximize} \DeclareMathOperator*{\minimize}{minimize} \newcommand{\mle}{\textsf{ML}} \newcommand{\nimplies}{\;\not\!\!\!\!\implies} \newcommand{\orange}[1]{\color{orange}{#1}} \newcommand{\outcome}[1]{\textsf{#1}} \newcommand{\param}[1]{{\color{purple} #1}} \newcommand{\pgsamplespace}{\{\green{1},\green{2},\green{3},\purp{4},\purp{5},\purp{6}\}} \newcommand{\pedge}[2]{\require{enclose}\enclose{circle}{~{#1}~} \rightarrow \; \enclose{circle}{\kern.01em {#2}~\kern.01em}} \newcommand{\pnode}[1]{\require{enclose}\enclose{circle}{\kern.1em {#1} \kern.1em}} \newcommand{\ponode}[1]{\require{enclose}\enclose{box}[background=lightgray]{{#1}}} \newcommand{\pnodesp}[1]{\require{enclose}\enclose{circle}{~{#1}~}} \newcommand{\purp}[1]{\color{purple}{#1}} \newcommand{\sign}{\text{Sign}} \newcommand{\spacecap}{\; \cap \;} \newcommand{\spacewedge}{\; \wedge \;} \newcommand{\tails}{\outcome{tails}} \newcommand{\Var}[1]{\text{Var}[#1]} \newcommand{\bigVar}[1]{\text{Var}\mkern-4mu \left[ #1 \right]}

Prof. Jeff Introduction!

• Born and raised in NW DC → high school in Rockville, MD
• University of Maryland: Computer Science, Math, Economics (2008-2012)

Grad School

• Studied abroad in Beijing (Peking University/北大) → internship with Huawei in Hong Kong (HKUST)

• Stanford for MS in Computer Science (2012-2014)
• Research Economist at UC Berkeley (2014-2015)

• Columbia for PhD[+Postdoc] in Political Science (2015-2023)

Dissertation (Political Science + History)

“Our Word is Our Weapon”: Text-Analyzing Wars of Ideas from the French Revolution to the First Intifada

Why Is Georgetown Having Me Teach This?

• Quanty things, but then PhD major was Political Philosophy (concentration in International Relations)
• What most interested me: unraveling history; Easy to get lost in “present-day” details of e.g. debiasing algorithms and fairness in AI, but these questions go back literally thousands of years!
• Pol philosophers distinguish “ancients” and “moderns” based on a crucial shift in perspective: ancients sought perfection, while Rousseau (1762) “took men [sic] as they are, and laws as they could be”.

Figure 1: Years spent questing in various dungeons of academia

• But is separation of ethics from politics possible? (Bowles 2016) Should we accept “human nature” as immutable/eternal? My answer: yes AND no simultaneously…

Dialectics

My Biases

• Upbringing: religious Jewish, right-wing (Revisionist Zionist) Republican environment
• “Encouraged” to emigrate to Israel for IDF service, but after learning history I renounced citizenship etc., family no longer big fans of me (Traumatic and scary to talk about, tbh 🙈)
• 2015-present: Teach CS + design thinking in refugee camps in West Bank and Gaza each summer (Code for Palestine)
• Metaethics: Learn about the world, challenge+update prior beliefs (Bayes’ rule!); I hope to challenge+update them throughout semester, with your help 🙂

On the One Hand…

On the Other Hand…

Remembering Why It Matters

Rules of Thumb

• Ask questions about power \leadsto inequities, but especially about structures/processes that give rise to them!
• “Philosophers have hitherto only tried to understand the world; the point, however, is to change it.” (Marx 1845)
• Dialectical implication: the more we understand it the better we’ll be at changing it

Ricardo Morales Art Studio

Ethics as an Axiomatic System

Axiomatics

• Popular understanding of math: Deals with Facts, statements are true or false
  • Ex: 1 + 1 = 2 is “true”
• Reality: No statements in math are absolutely true! Only conditional statements are possible to prove!
• We cannot prove atomic statements q, only implicational statements: p \implies q for some axiom(s) p.
• 1 + 1 = 2 is indeterminate without definitions of 1, +, =, and 2!
  • (Easy counterexample for math/CS majors: 1 + 1 = 0 in \mathbb{Z}_2)

Steingart (2023)

Example: 1 + 1 = 2

• How it’s taught: this is a rule, and if you don’t follow it you will be banished to eternal hellfire
• How it’s proved: ZFC \implies [1 + 1 = 2], where ZFC stands for the Zermelo-Fraenkel Axioms with the Axiom of Choice!

Whitehead and Russell (1910), p. 83. See here for page in context

Proving 1 + 1 = 2

(A non-formal proof that still captures the gist:)

• Axiom 1: There is a type of thing that can hold other things, which we’ll call a set. We’ll represent it like: \{ \langle \text{\text{stuff in the set}} \rangle \}.
• Axiom 2: Start with the set with nothing in it, \{\}, and call it “0”.
• Axiom 3: If we put this set 0 inside of an empty set, we get a new set \{0\} = \{\{\}\}, which we’ll call “1”.
• Axiom 4: If we put this set 1 inside of another set, we get another new set \{1\} = \{\{\{\}\}\}, which we’ll call “2”.
• Axiom 5: This operation (creating a “next number” by placing a given number inside an empty set) we’ll call succession: S(x) = \{x\}
• Axiom 6: We’ll define addition, a + b, as applying this succession operation S to a, b times. Thus a + b = \underbrace{S(S(\cdots (S(}_{b\text{ times}}a))\cdots ))
• Result: (Axioms 1-6) \implies 1 + 1 = S(1) = S(\{\{\}\}) = \{\{\{\}\}\} = 2. \; \blacksquare

How Is This Relevant to Ethics?

(Thank you for bearing with me on that 😅)

• Just as mathematicians slowly came to the realization that

\textbf{mathematical results} \neq \textbf{(non-implicational) truths}

• I hope to help you see how

\textbf{ethical conclusions} \neq \textbf{(non-implicational) truths}

• When someone says 1 + 1 = 2, you are allowed to question them, and ask, “On what basis? Please explain…”.
  • Here the only valid answer is a collection of axioms which entail 1 + 1 = 2
• When someone says Israel has the right to defend itself, you are allowed to question them, and ask, “On what basis? Please explain…”
  • Here the only valid answer is an ethical framework which entails that Israel has the right to defend itself.

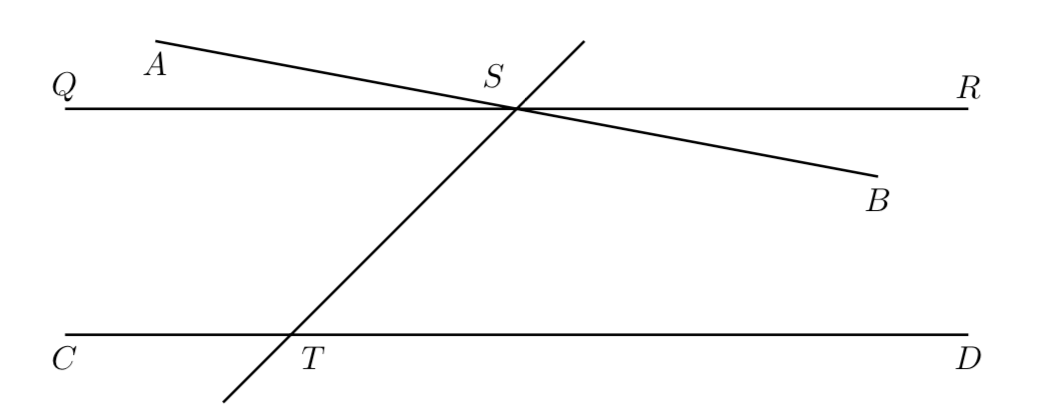
Axiomatic Systems: Statements Can Be True And False

• Let T be sum of interior angles of a triangle. We’re taught [T = 180^\circ] as a “rule”
• Euclid’s Fifth Postulate P_5: Given a line and a point not on it, exactly one line parallel to the given line can be drawn through the point.

P_5 \implies T = 180^\circ (Euclidean Geometry)

\neg P_5 \implies T \neq 180^\circ (Non-Euclidean Geometry)

References

Bowles, Samuel. 2016. The Moral Economy: Why Good Incentives Are No Substitute for Good Citizens. Yale University Press. https://books.google.com?id=Q7IODAAAQBAJ.

Marx, Karl. 1845. Thesen über Feuerbach. Stuttgart: J. H. W. Dietz. https://de.wikisource.org/wiki/Thesen_%C3%BCber_Feuerbach.

Rousseau, Jean-Jacques. 1762. The Social Contract. Geneva: J. M. Dent. https://books.google.com?id=G1MOAQAAIAAJ.

Steingart, Alma. 2023. Axiomatics: Mathematical Thought and High Modernism. University of Chicago Press. https://books.google.com?id=VLmeEAAAQBAJ.

Whitehead, Alfred North, and Bertrand Russell. 1910. Principia Mathematica. Cambridge University Press. https://books.google.com?id=SB440AEACAAJ.