Week 7: Basis Functions and Splines
DSAN 5300: Statistical Learning
Spring 2025, Georgetown University
Monday, February 24, 2025
Schedule
Today’s Planned Schedule:
| Start | End | Topic | |
|---|---|---|---|
| Lecture | 6:30pm | 7:00pm | Roadmap: Even More Wiggly “Linearity” → |
| 7:00pm | 7:20pm | “Manual” Model Selection: Subsets → | |
| 7:20pm | 7:40pm | Key Regularization Building Block: \(L^p\) Norm → | |
| 7:40pm | 8:00pm | Regularized Regression Intro → | |
| Break! | 8:00pm | 8:10pm | |
| 8:10pm | 8:50pm | Basically Lasso is the Coolest Thing Ever → | |
| 8:50pm | 9:00pm | Scary-Looking But Actually-Fun W07 Preview → |
\[ \DeclareMathOperator*{\argmax}{argmax} \DeclareMathOperator*{\argmin}{argmin} \newcommand{\bigexp}[1]{\exp\mkern-4mu\left[ #1 \right]} \newcommand{\bigexpect}[1]{\mathbb{E}\mkern-4mu \left[ #1 \right]} \newcommand{\definedas}{\overset{\small\text{def}}{=}} \newcommand{\definedalign}{\overset{\phantom{\text{defn}}}{=}} \newcommand{\eqeventual}{\overset{\text{eventually}}{=}} \newcommand{\Err}{\text{Err}} \newcommand{\expect}[1]{\mathbb{E}[#1]} \newcommand{\expectsq}[1]{\mathbb{E}^2[#1]} \newcommand{\fw}[1]{\texttt{#1}} \newcommand{\given}{\mid} \newcommand{\green}[1]{\color{green}{#1}} \newcommand{\heads}{\outcome{heads}} \newcommand{\iid}{\overset{\text{\small{iid}}}{\sim}} \newcommand{\lik}{\mathcal{L}} \newcommand{\loglik}{\ell} \DeclareMathOperator*{\maximize}{maximize} \DeclareMathOperator*{\minimize}{minimize} \newcommand{\mle}{\textsf{ML}} \newcommand{\nimplies}{\;\not\!\!\!\!\implies} \newcommand{\orange}[1]{\color{orange}{#1}} \newcommand{\outcome}[1]{\textsf{#1}} \newcommand{\param}[1]{{\color{purple} #1}} \newcommand{\pgsamplespace}{\{\green{1},\green{2},\green{3},\purp{4},\purp{5},\purp{6}\}} \newcommand{\prob}[1]{P\left( #1 \right)} \newcommand{\purp}[1]{\color{purple}{#1}} \newcommand{\sign}{\text{Sign}} \newcommand{\spacecap}{\; \cap \;} \newcommand{\spacewedge}{\; \wedge \;} \newcommand{\tails}{\outcome{tails}} \newcommand{\Var}[1]{\text{Var}[#1]} \newcommand{\bigVar}[1]{\text{Var}\mkern-4mu \left[ #1 \right]} \]
Roadmap
[Weeks 4-6]
Polynomial Regression
Linear Models
Piecewise Regression
Linear Models
[Today]
Splines (Truncated Power Bases)
Linear Models
Natural Splines
Linear Models
What Problem Are We Solving?
- From W04-06, you are now really good at thinking through issues of non-linearity in terms of polynomial regression
- (Hence, why I kept “plugging in” degree of polynomial as our measure of complexity)
- Now we want to move towards handling any kind of non-linearity
- (Hence, why I kept reminding you how degree of polynomial is only one possible measure of complexity)
What’s So Bad About Polynomial Regression?
- Mathematically, Weierstrass Approximation Theorem says we can model any function as (possibly infinite) sum of polynomials
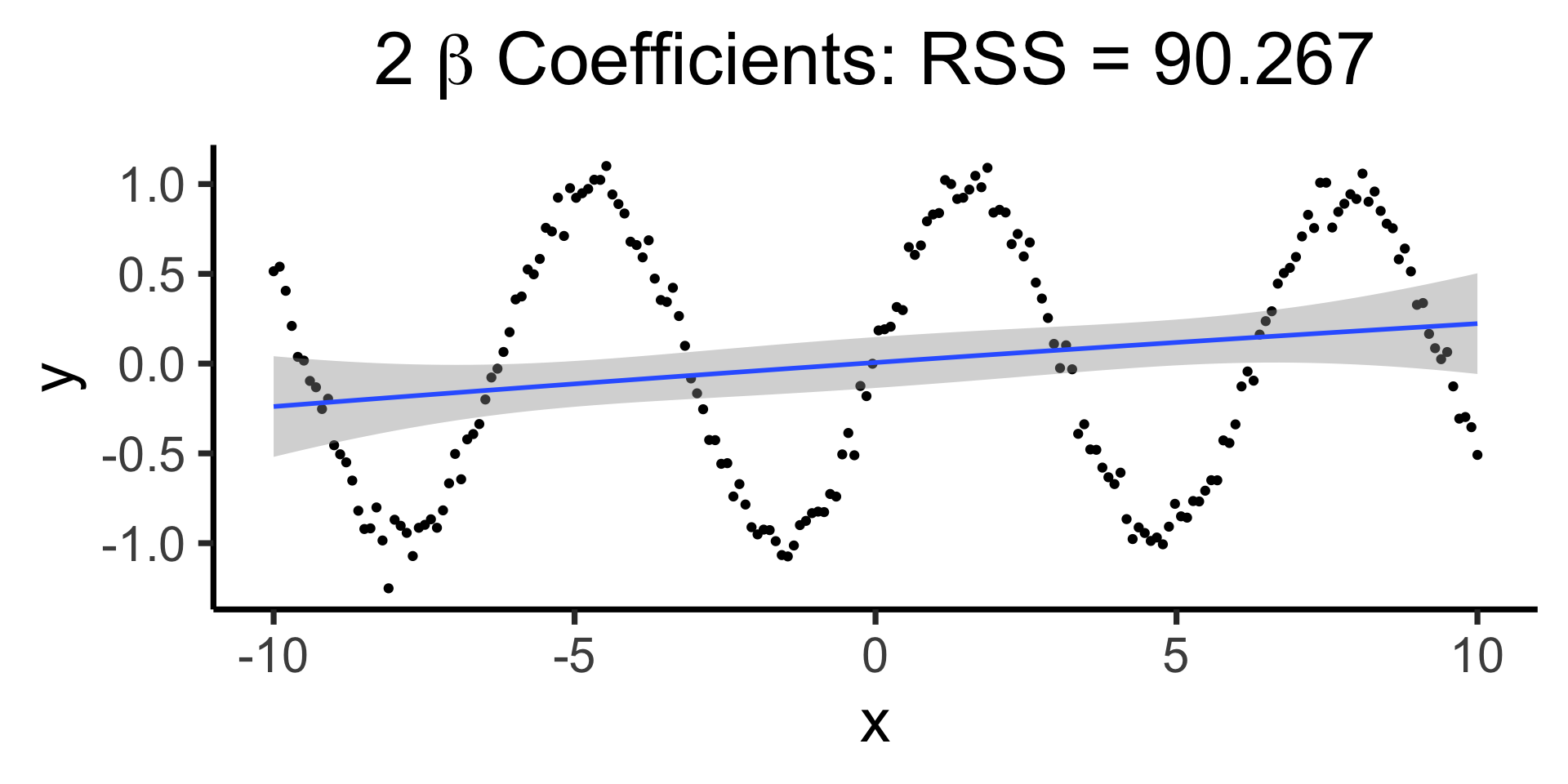
- In practice, this can be a horrifically bad way to actually model things:
Raw data: \(y = \sin(x) + \varepsilon\)
Code
library(tidyverse) |> suppressPackageStartupMessages()
library(latex2exp) |> suppressPackageStartupMessages()
N <- 200
x_vals <- seq(from=-10, to=10, length.out=N)
y_raw <- sin(x_vals)
y_noise <- rnorm(length(y_raw), mean=0, sd=0.075)
y_vals <- y_raw + y_noise
dgp_label <- TeX("Raw Data")
data_df <- tibble(x=x_vals, y=y_vals)
base_plot <- data_df |> ggplot(aes(x=x, y=y)) +
geom_point() +
theme_dsan(base_size=28)
base_plot + labs(title=dgp_label)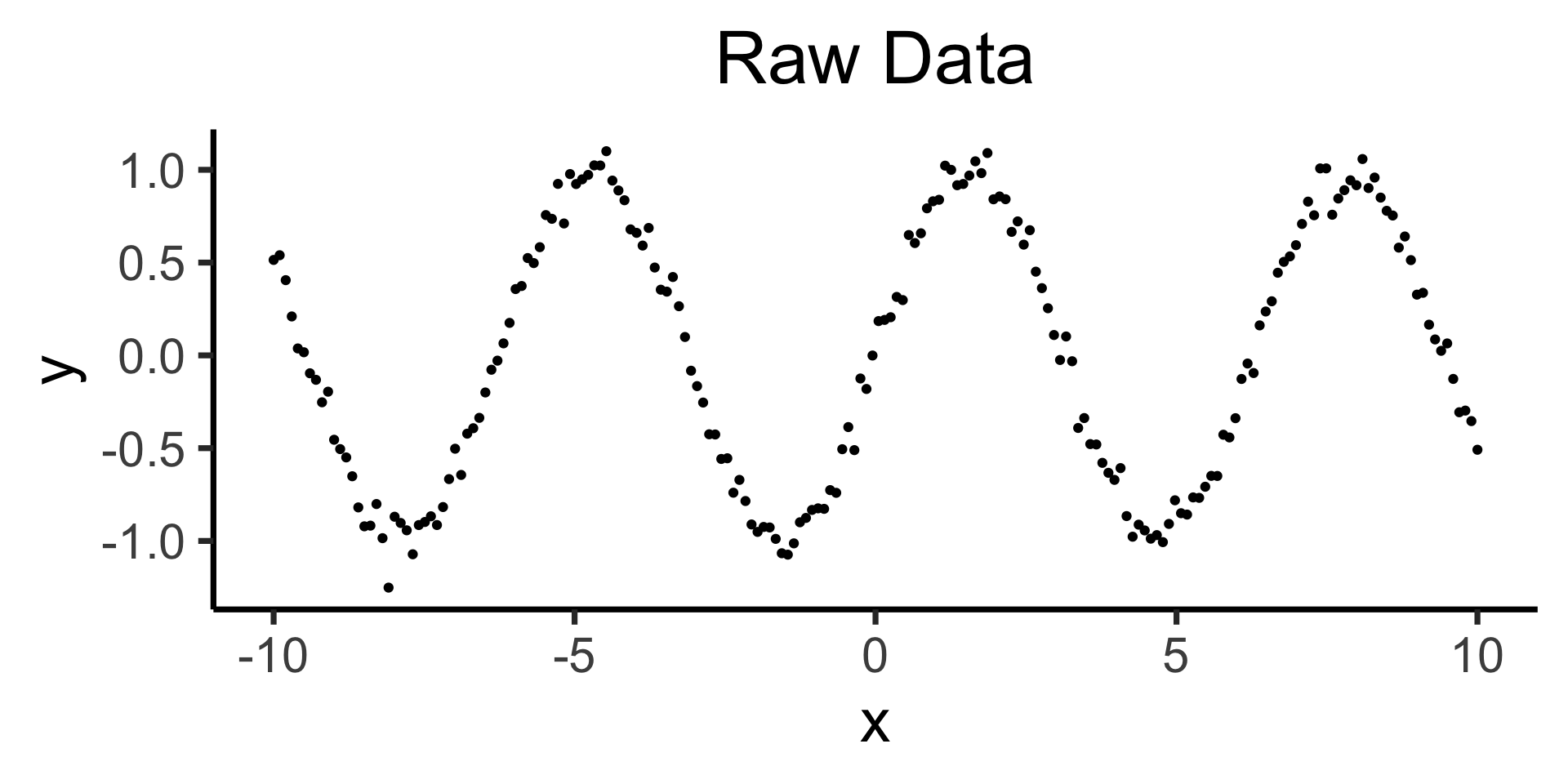
Bad (quadratic) model
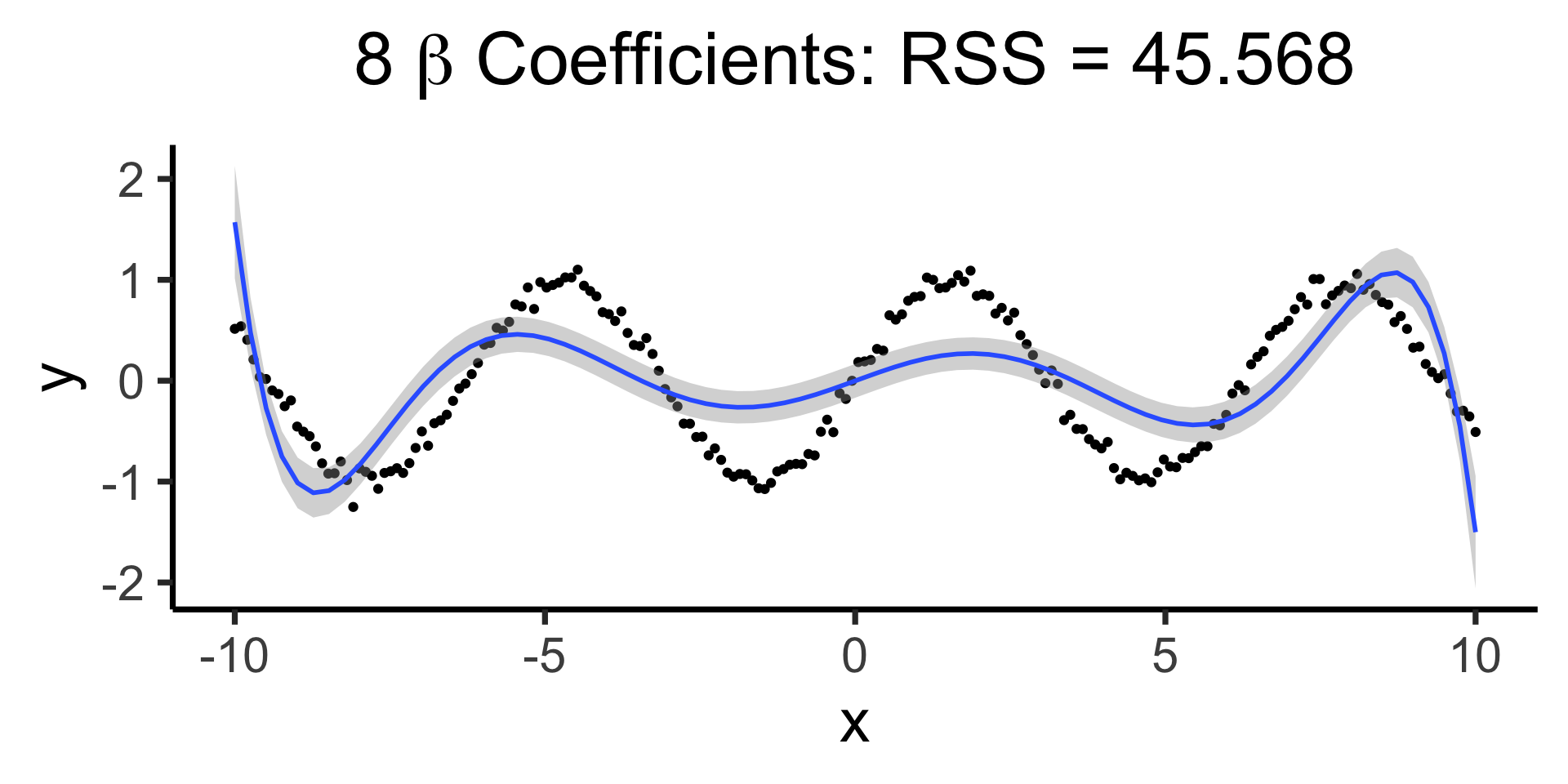
Making it “better” with more complex polynomials
Code
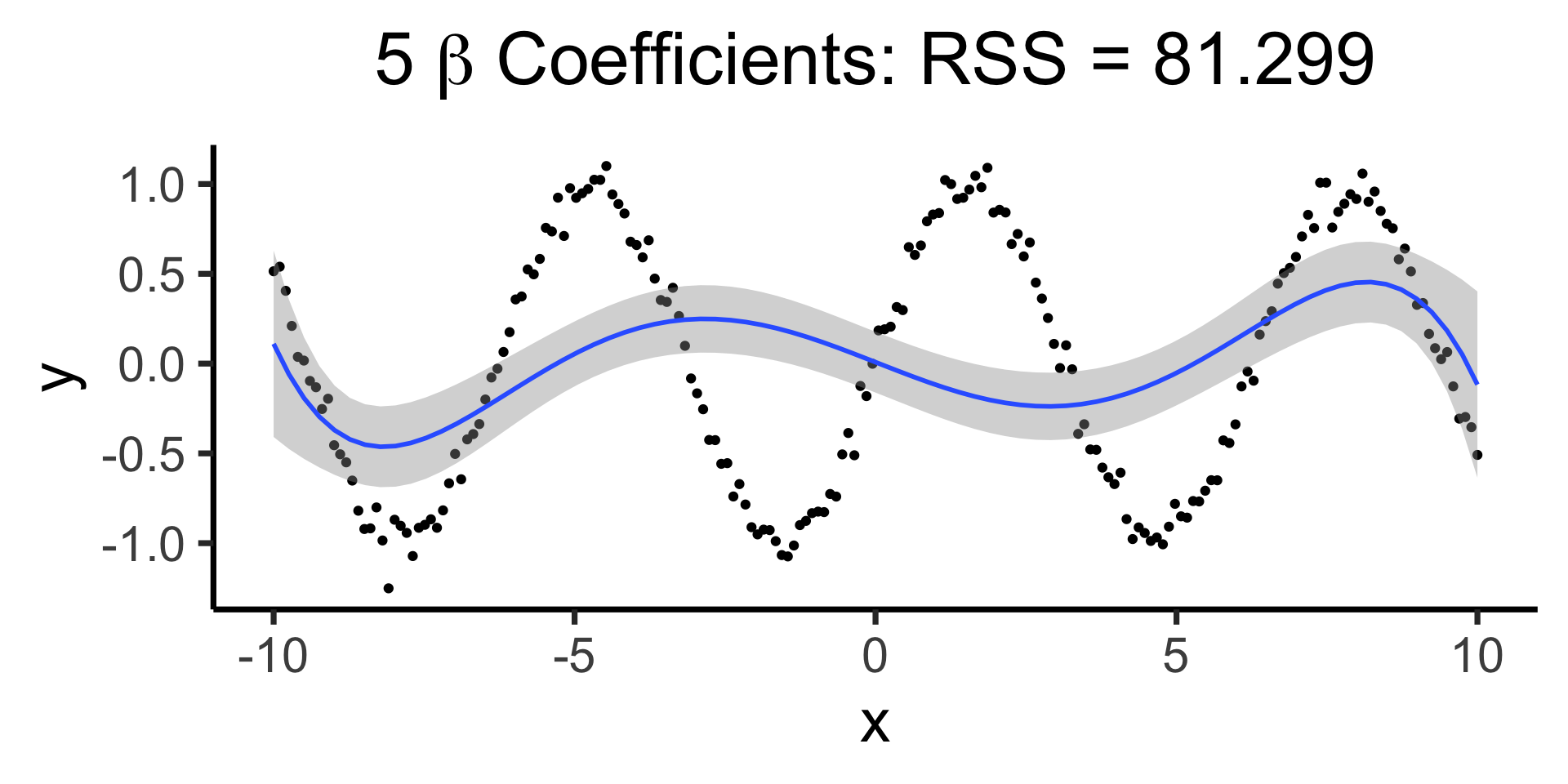
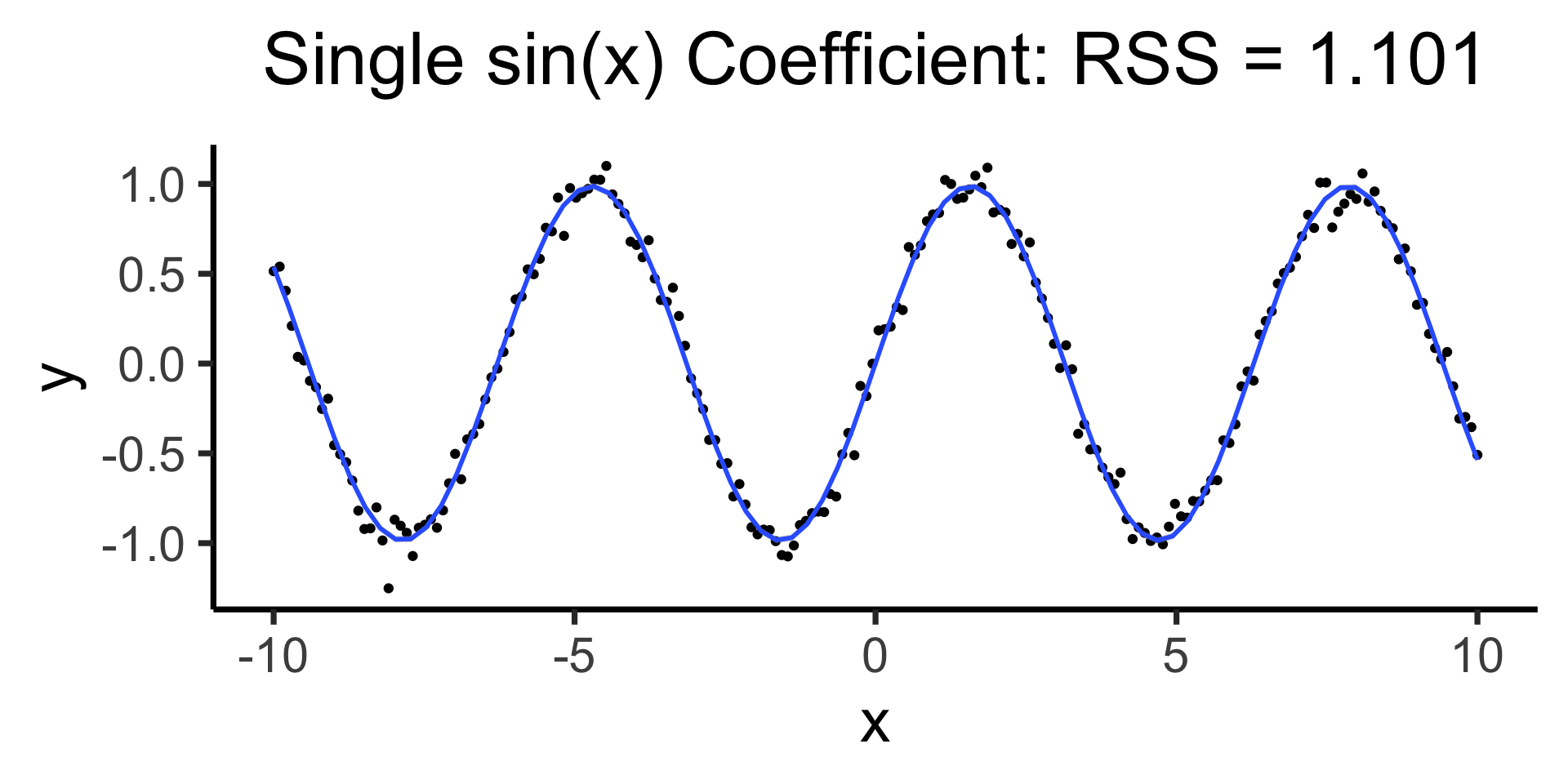
Using all data to estimate single parameter, by using the “correct” basis function!
\[ Y = \beta_0 + \beta_1 \sin(x) \]
Basis Functions
- Seems like it’ll help to have a toolkit filled with different basis functions, so we can use them with
lm()🤔 - …Let’s get into it!
The General Form
(Decomposing Fancy Regressions into Core “Pieces”)
Q: What do all these types of regression have in common?
A: They can all be written in the form
\[ Y = \beta_0 + \beta_1 b_1(X) + \beta_2 b_2(X) + \cdots + \beta_d b_d(X) \]
Where \(b(\cdot)\) is called a basis function
- Polynomial: \(b_j(X) = X^j\)
- Piecewise: \(b_j(X) = \mathbb{1}[c_{j-1} \leq X < c_j]\)
- Earlier Example: \(b_1(X) = \sin(X)\)
Segments \(\rightarrow\) Splines
| What we want | How we do it | Name for result | |
|---|---|---|---|
| Model sub-regions of \(\text{domain}(X)\) | Chop \(\text{domain}(X)\) into pieces, one regression per piece | Discontinuous Segmented Regression | |
| Continuous prediction function | Require pieces to join at chop points \(\{\xi_1, \ldots, \xi_K\}\) | Continuous Segmented Regression | |
| Smooth prediction function | Require pieces to join and have equal derivatives at \(\xi_i\) | Spline | |
| Less jump in variance at boundaries | Reduce complexity of polynomials at endpoints | Natural Spline |
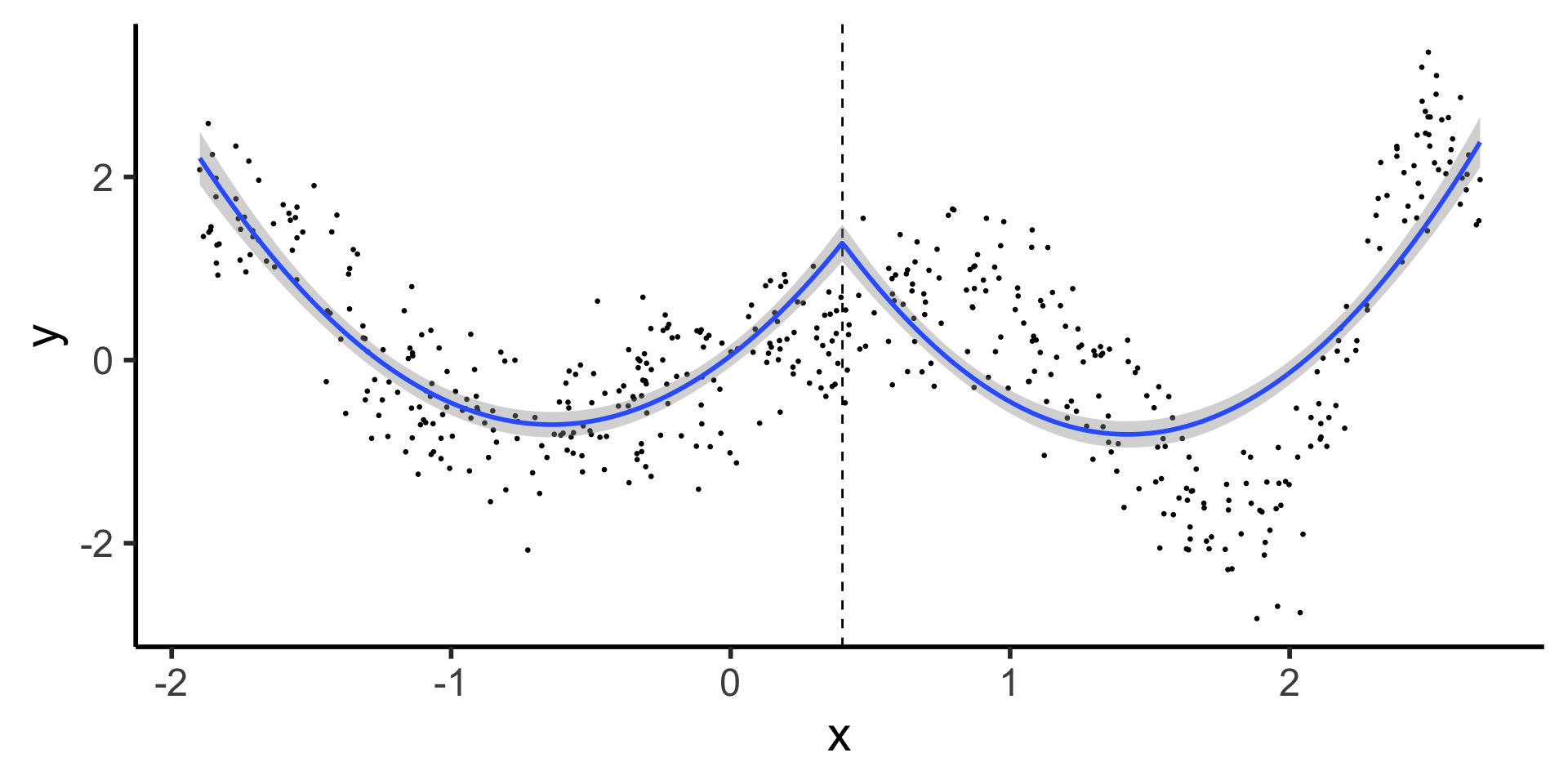
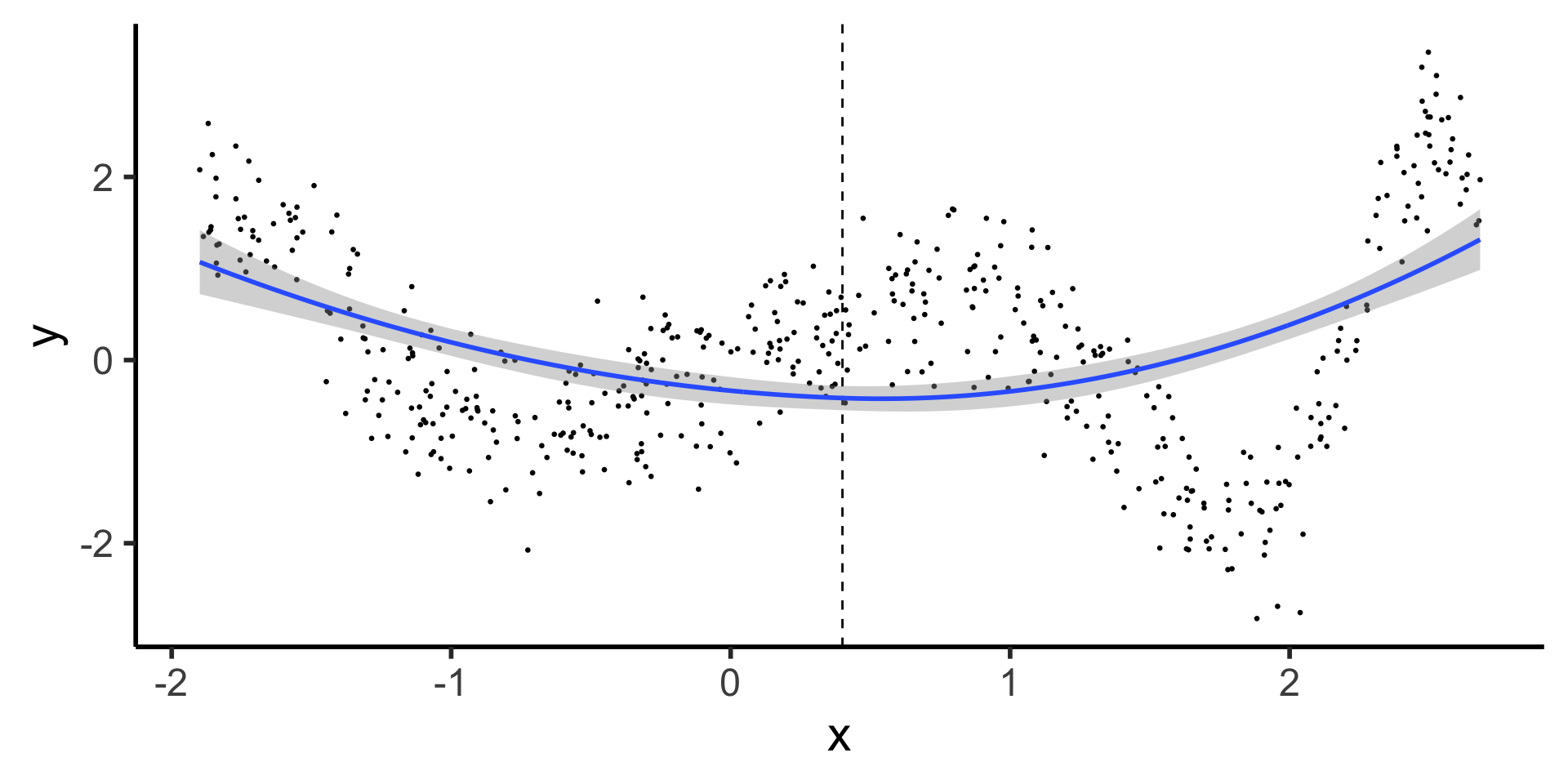
Discontinuous Segmented Regression
- Here we see why our first two basis functions were polynomial and piecewise: most rudimentary spline fits a polynomial to each piece
Code
library(tidyverse) |> suppressPackageStartupMessages()
set.seed(5300)
compute_y <- function(x) {
return(x * cos(x^2))
}
N <- 500
xmin <- -1.9
xmax <- 2.7
x_vals <- runif(N, min=xmin, max=xmax)
y_raw = compute_y(x_vals)
y_noise = rnorm(N, mean=0, sd=0.5)
y_vals <- y_raw + y_noise
prod_df <- tibble(x=x_vals, y=y_vals)
knot <- (xmin + xmax) / 2
prod_df <- prod_df |> mutate(segment = x <= knot)
# First segment model
#left_df <- prod_df |> filter(x <= knot_point)
#left_model <- lm(y ~ poly(x, 2), data=left_df)
prod_df |> ggplot(aes(x=x, y=y, group=segment)) +
geom_point(size=0.5) +
geom_vline(xintercept=knot, linetype="dashed") +
geom_smooth(method='lm', formula=y ~ poly(x, 2), se=TRUE) +
theme_classic(base_size=22)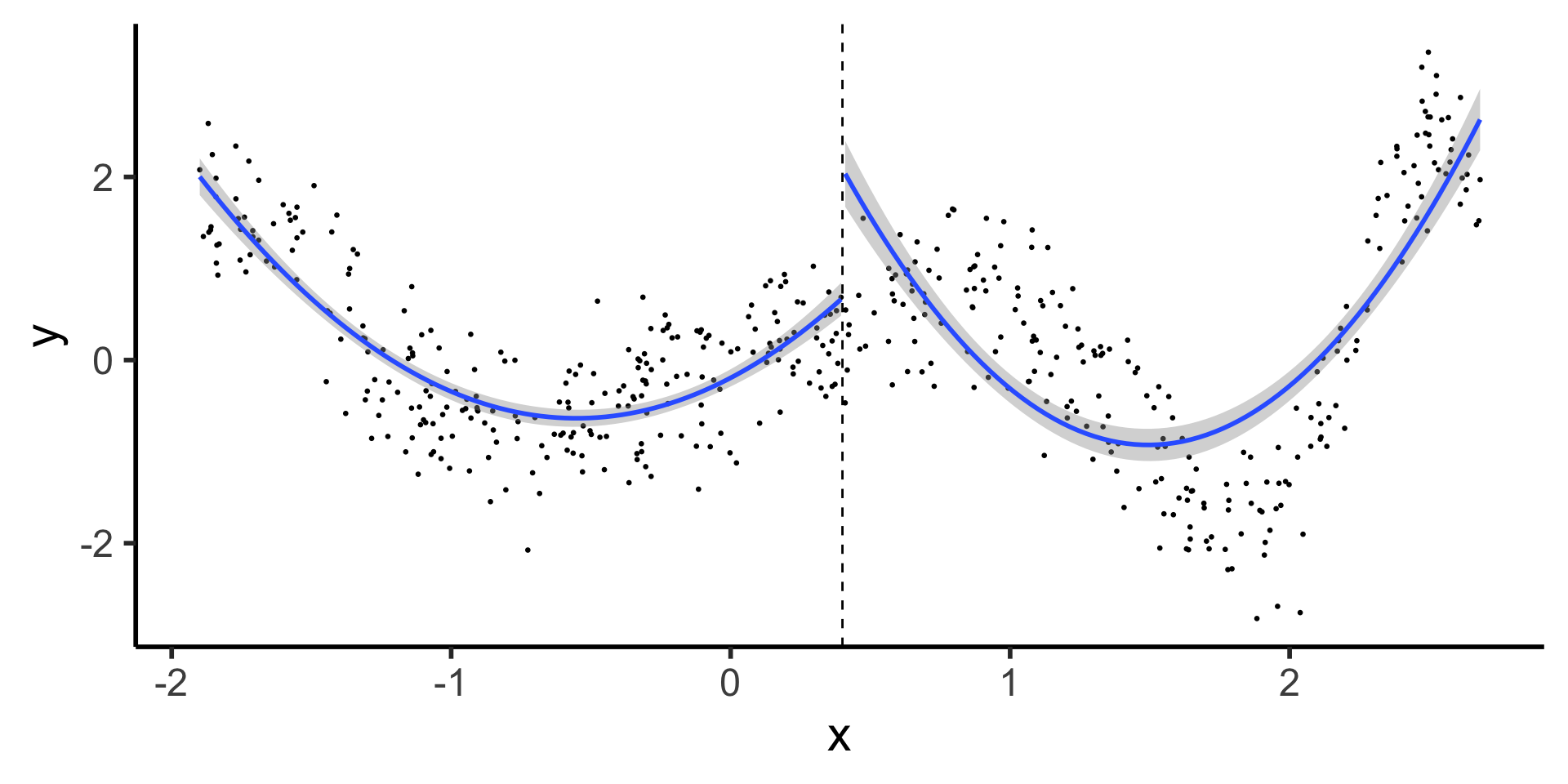
- What’s the issue with this?
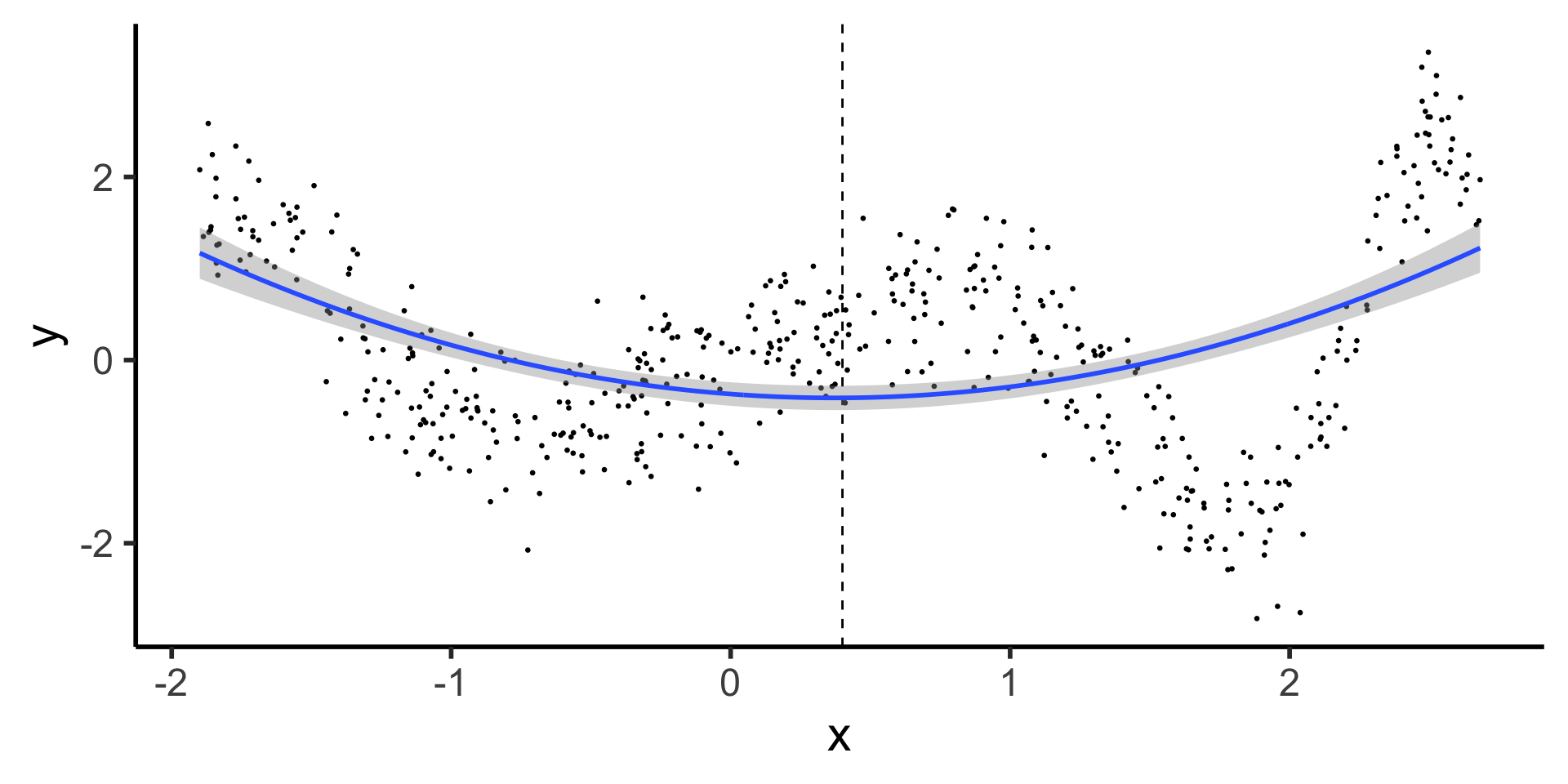
Forcing Continuity at Knot Points
- Starting slow: let’s come back down to line world…
- Why are these two lines “allowed” to be non-continuous, under our current approach?
\[ \hspace{6.5cm} Y^{\phantom{🧐}}_L = \beta_0 + \beta_1 X_L \]
\[ Y_R = \beta_0^{🧐} + \beta_1 X_R \hspace{5cm} \]
Code
set.seed(5300)
xmin_sub <- -1
xmax_sub <- 1.9
sub_df <- prod_df |> filter(x >= xmin_sub & x <= xmax_sub)
sub_knot <- (xmin_sub + xmax_sub) / 2
sub_df <- sub_df |> mutate(segment = x <= sub_knot)
# First segment model
sub_df |> ggplot(aes(x=x, y=y, group=segment)) +
geom_point(size=0.5) +
geom_vline(xintercept=sub_knot, linetype="dashed") +
geom_smooth(method='lm', formula=y ~ x, se=TRUE, linewidth=g_linewidth) +
theme_classic(base_size=28)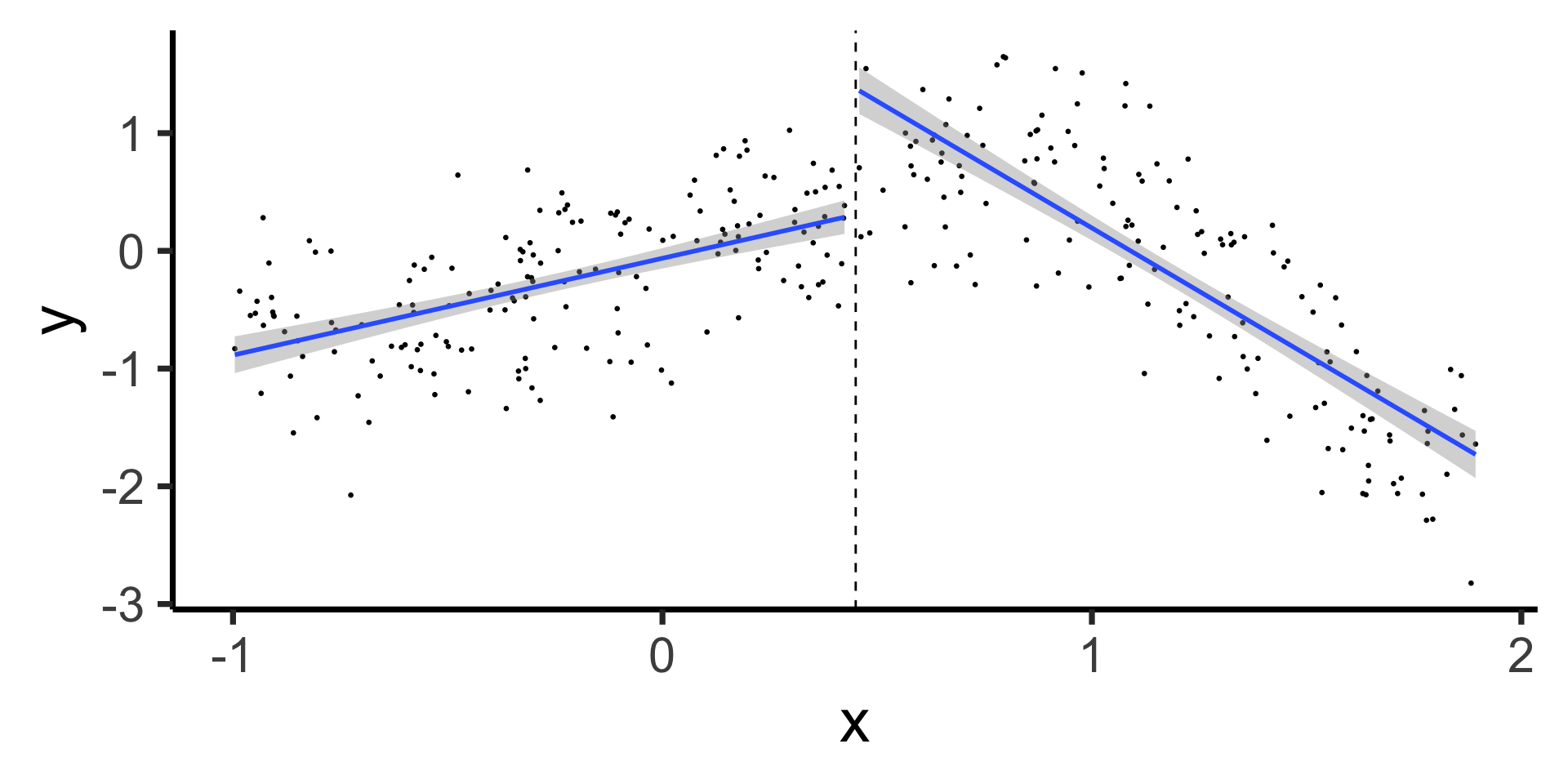
- …We need \(X_R\) to have its own slope but not its own intercept! Something like:
\[ Y = \beta_0 + \beta_1 (X \text{ before } \xi) + \beta_2 (X \text{ after } \xi) \]
Truncated Power Basis (ReLU Basis)
\[ \text{ReLU}(x) \definedas (x)_+ \definedas \begin{cases} 0 &\text{if }x \leq 0 \\ x &\text{if }x > 0 \end{cases} \implies (x - \xi)_+ = \begin{cases} 0 &\text{if }x \leq \xi \\ x - \xi &\text{if }x > 0 \end{cases} \]
Code
library(latex2exp) |> suppressPackageStartupMessages()
trunc_x <- function(x, xi) {
return(ifelse(x <= xi, 0, x - xi))
}
trunc_x_05 <- function(x) trunc_x(x, 1/2)
trunc_title <- TeX("$(x - \\xi)_+$ with $\\xi = 0.5$")
trunc_label <- TeX("$y = (x - \\xi)_+$")
ggplot() +
stat_function(
data=data.frame(x=c(-3,3)),
fun=trunc_x_05,
linewidth=g_linewidth
) +
xlim(-3, 3) +
theme_dsan(base_size=28) +
labs(
title = trunc_title,
x = "x",
y = trunc_label
)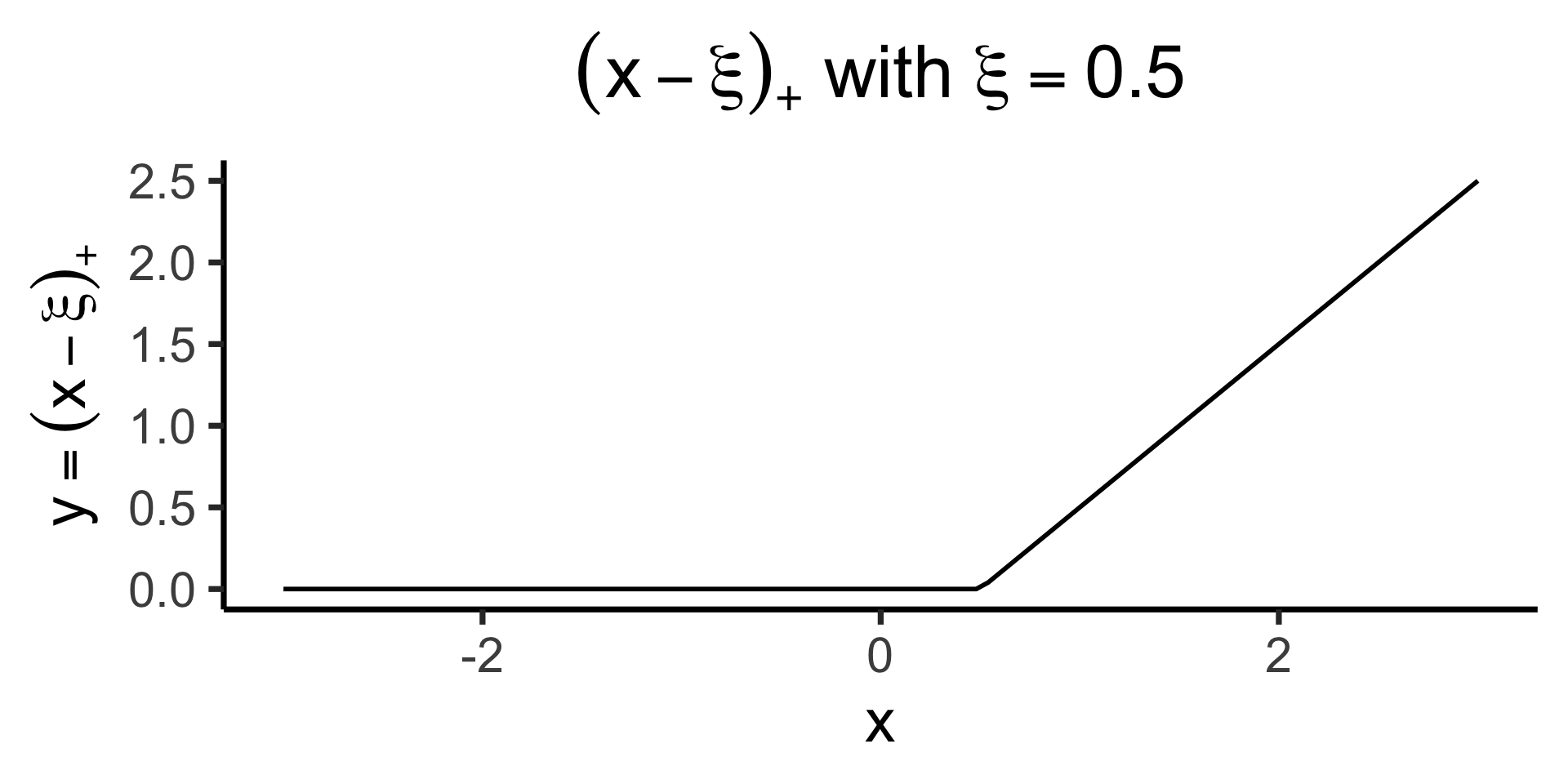
- \(\Rightarrow\) we can include a “slope modifier” \(\beta_m (X - \xi)_+\) that only “kicks in” once \(x\) goes past \(\xi\)! (Changing slope by \(\beta_m\))
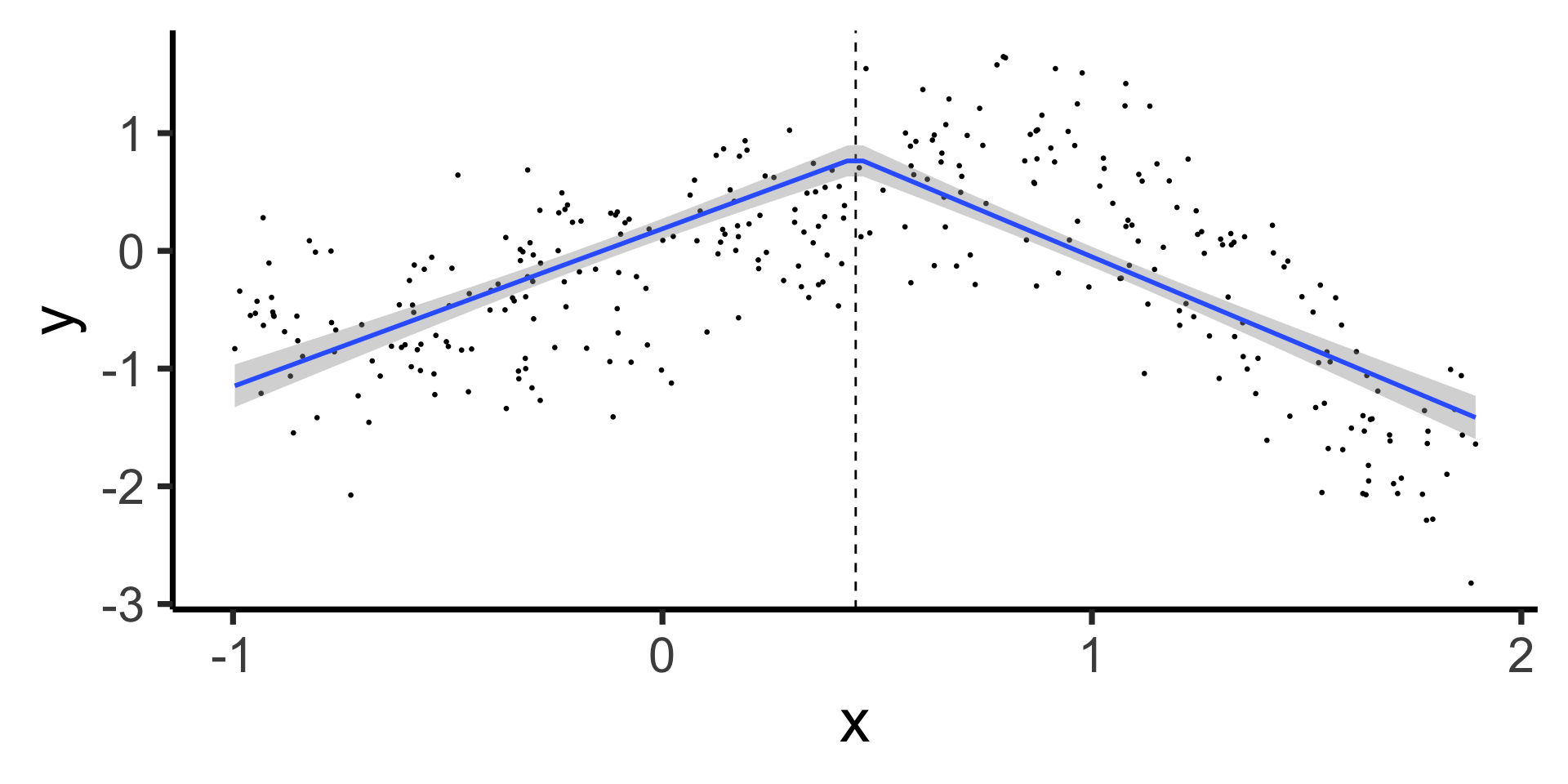
Linear Segments with Continuity at Knot
Our new (non-naïve) model:
\[ \begin{align*} Y &= \beta_0 + \beta_1 X + \beta_2 (X - \xi)_+ \\ &= \beta_0 + \begin{cases} \beta_1 X &\text{if }X \leq \xi \\ (\beta_1 + \beta_2)X &\text{if }X > \xi \end{cases} \end{align*} \]
Code
| term | estimate | std.error | statistic |
|---|---|---|---|
| (Intercept) | 0.187 | 0.044 | 4.255 |
| x | 1.340 | 0.093 | 14.342 |
| x_tr | -2.868 | 0.168 | -17.095 |
Continuous Segmented Regression
\[ \begin{align*} Y &= \beta_0 + \beta_1 X + \beta_2 X^2 + \beta_3 (X - \xi)_+ + \beta_4 (X - \xi)_+^2 \\[0.8em] &= \beta_0 + \begin{cases} \beta_1 X + \beta_2 X^2 &\text{if }X \leq \xi \\ (\beta_1 + \beta_3) X + (\beta_2 + \beta_4) X^2 &\text{if }X > \xi \end{cases} \end{align*} \]
Code
cont_seg_plot <- ggplot() +
geom_point(data=prod_df, aes(x=x, y=y), size=0.5) +
geom_vline(xintercept=knot, linetype="dashed") +
stat_smooth(
data=prod_df, aes(x=x, y=y),
method='lm',
formula=y ~ poly(x,2) + poly(ifelse(x > knot, (x - knot), 0), 2),
n = 300
) +
#geom_smooth(data=prod_df |> filter(segment == FALSE), aes(x=x, y=y), method='lm', formula=y ~ poly(x,2)) +
# geom_smooth(method=segreg, formula=y ~ seg(x, npsi=1, fixed.psi=0.5)) + # + seg(I(x^2), npsi=1)) +
theme_classic(base_size=22)
cont_seg_plot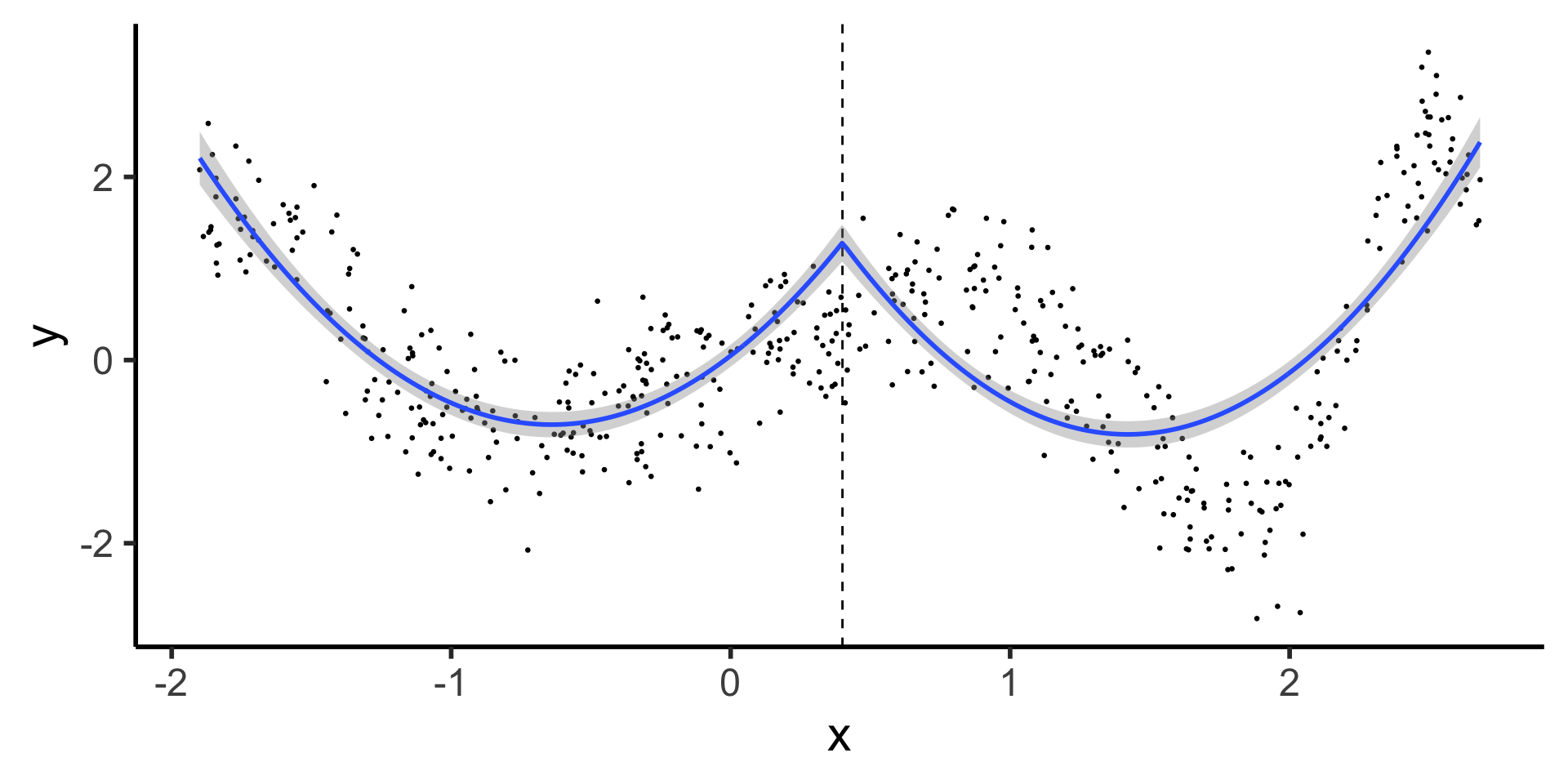
- There’s still a problem here… can you see what it is? (Hint: things that break calculus)
Splines (The Moment You’ve Been Waiting For!)
Constrained Derivatives: “Quadratic Splines” (⚠️)
- Like “Linear Probability Models”, “Quadratic Splines” are a red flag
- Why? If we have leftmost plot below, but want it differentiable everywhere… only option is to fit a single quadratic, defeating the whole point of the “chopping”!
\[ \frac{\partial Y}{\partial X} = \beta_1 + 2\beta_2 X + \beta_3 + 2\beta_4 X \]
“Quadratic Spline”:
- \(\implies\) Least-complex function that allows smooth “joining” is cubic function
Cubic Splines (aka, Splines)
(We did it, we finally did it)
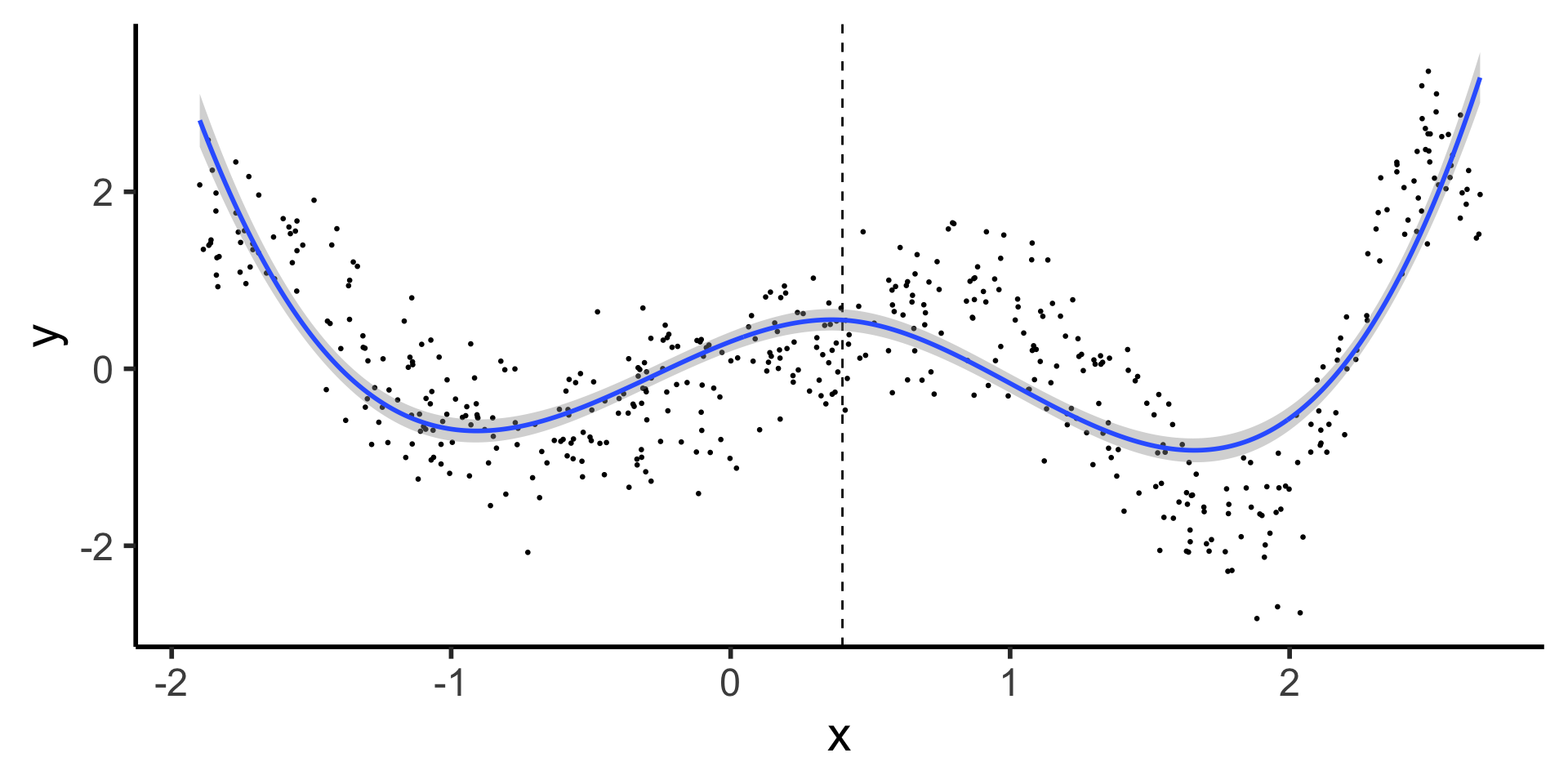
Natural Splines: Why Not Stop There?
Polynomials start to BEHAVE BADLY as they go to \(-\infty\) and \(\infty\)
Code
library(splines) |> suppressPackageStartupMessages()
set.seed(5300)
N_sparse <- 400
x_vals <- runif(N_sparse, min=xmin, max=xmax)
y_raw = compute_y(x_vals)
y_noise = rnorm(N_sparse, mean=0, sd=1.0)
y_vals <- y_raw + y_noise
sparse_df <- tibble(x=x_vals, y=y_vals)
knot_sparse <- (xmin + xmax) / 2
knot_vec <- c(-1.8,-1.7,-1.6,-1.5,-1.4,-1.2,-1.0,-0.8,-0.6,-0.4,-0.2,0,knot_sparse,1,1.5,2)
knot_df <- tibble(knot=knot_vec)
# Boundary lines
left_bound_line <- geom_vline(
xintercept = xmin + 0.1, linewidth=1,
color="red", alpha=0.8
)
right_bound_line <- geom_vline(
xintercept = xmax - 0.1,
linewidth=1, color="red", alpha=0.8
)
ggplot() +
geom_point(data=sparse_df, aes(x=x, y=y), size=0.5) +
geom_vline(
data=knot_df, aes(xintercept=knot),
linetype="dashed"
) +
stat_smooth(
data=sparse_df, aes(x=x, y=y),
method='lm',
formula=y ~ bs(x, knots=c(knot_sparse), degree=25),
n=300
) +
left_bound_line +
right_bound_line +
theme_dsan(base_size=22)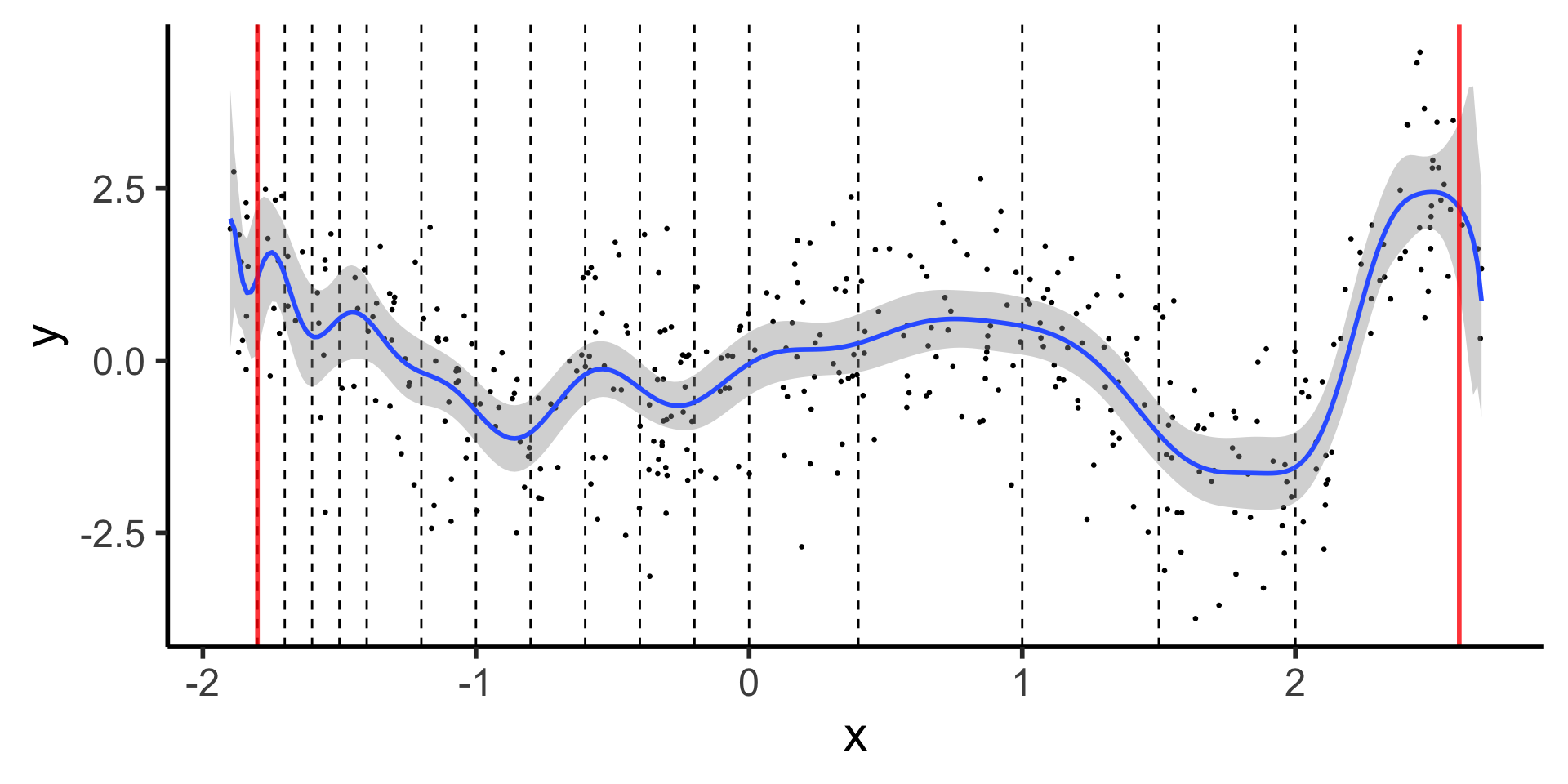
Natural Splines: Force leftmost and rightmost pieces to be linear
Code
library(splines) |> suppressPackageStartupMessages()
set.seed(5300)
N_sparse <- 400
x_vals <- runif(N_sparse, min=xmin, max=xmax)
y_raw = compute_y(x_vals)
y_noise = rnorm(N_sparse, mean=0, sd=1.0)
y_vals <- y_raw + y_noise
sparse_df <- tibble(x=x_vals, y=y_vals)
knot_sparse <- (xmin + xmax) / 2
ggplot() +
geom_point(data=sparse_df, aes(x=x, y=y), size=0.5) +
stat_smooth(
data=sparse_df, aes(x=x, y=y),
method='lm',
formula=y ~ ns(x, knots=knot_vec, Boundary.knots=c(xmin + 0.1, xmax - 0.1)),
n=300
) +
geom_vline(
data=knot_df, aes(xintercept=knot),
linetype="dashed"
) +
left_bound_line +
right_bound_line +
theme_dsan(base_size=22)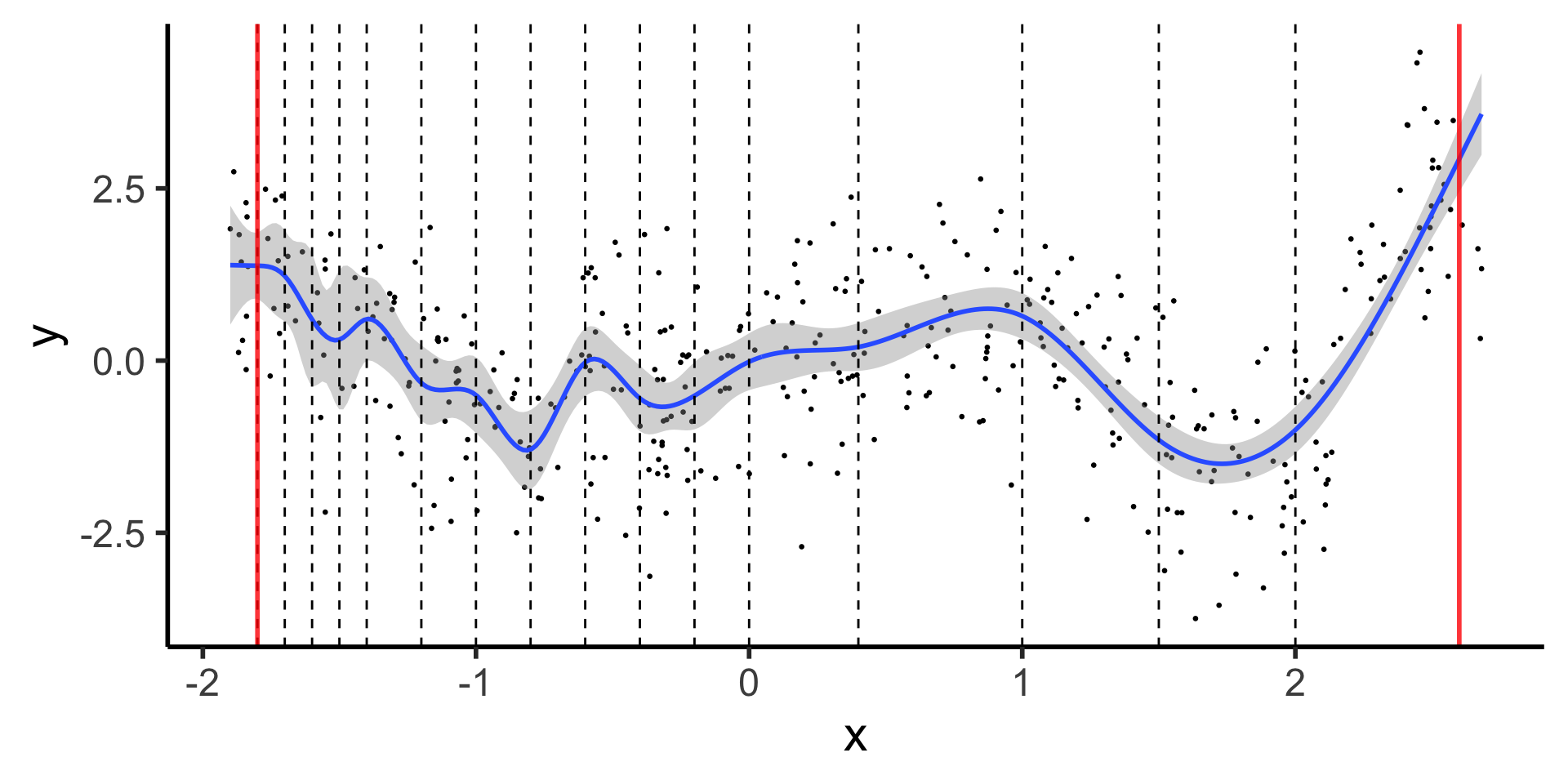
How Do We Find The Magical Knot Points?
- Hyperparameter 0: Number of knots \(K\)
- Hyperparameters 1 to \(K\): Location \(\xi_k\) for each knot
- Fear: Seems like we’re going to need a bunch of slides/lectures talking about this, right?
- (e.g., if you really do have to manually choose them, heuristic is to place them in more “volatile” parts of \(D_X\))
- Reality: Nope, just use CV! 😉😎
Even Cooler Alternative Approach: Smoothing Splines
(Where “cooler” here really means “more statistically-principled”)
Reminder (W04): Penalizing Complexity
Week 4 (General Form):
\[ \boldsymbol\theta^* = \underset{\boldsymbol\theta}{\operatorname{argmin}} \left[ \mathcal{L}(y, \widehat{y}; \boldsymbol\theta) + \lambda \cdot \mathsf{Complexity}(\boldsymbol\theta) \right] \]

Last Week (Penalizing Polynomials):
\[ \boldsymbol\beta^*_{\text{lasso}} = \underset{\boldsymbol\beta, \lambda}{\operatorname{argmin}} \left[ \frac{1}{N}\sum_{i=1}^{N}(\widehat{y}_i(\boldsymbol\beta) - y_i)^2 + \lambda \|\boldsymbol\beta\|_1 \right] \]

Now (Penalizing Sharp Change / Wigglyness):
\[ g^* = \underset{g, \lambda}{\operatorname{argmin}} \left[ \sum_{i=1}^{N}(g(x_i) - y_i)^2 + \lambda \overbrace{\int}^{\mathclap{\text{Sum of}}} [\underbrace{g''(t)}_{\mathclap{\text{Change in }g'(t)}}]^2 \mathrm{d}t \right] \]

Penalizing Wiggles
\[ g^* = \underset{g, \lambda}{\operatorname{argmin}} \left[ \sum_{i=1}^{N}(g(x_i) - y_i)^2 + \lambda \overbrace{\int}^{\mathclap{\text{Sum of}}} [\underbrace{g''(t)}_{\mathclap{\text{Change in }g'(t)}}]^2 \mathrm{d}t \right] \]
- (Note that we do not assume it’s a spline! We optimize over \(g\) itself, not \(K\), \(\xi_k\))
- Penalizing \([g'(t)]^2\) would mean: penalize function for changing over its domain
- Penalizing \([g''(t)]^2\) means: it’s ok to change, but do so smoothly
- Uber ride metaphor: remember how \(g'(t)\) gives speed while \(g''(t)\) gives acceleration
- Penalizing speed… would just make driver go slowly (ensuring slow ride)
- Penalizing acceleration…
- Ensures that they can fit the traffic pattern (can drive whatever speed they want)
- As long as they smoothly accelerate and decelerate between those speeds (ensuring non-bumpy ride!)
Three Mind-Blowing Math Facts
As \(\lambda \rightarrow 0\), \(g^*\) will grow as wiggly as necessary to achieve zero RSS / MSE / \(R^2\)
As \(\lambda \rightarrow \infty\), \(g^*\) converges to OLS linear regression line
We didn’t optimize over splines, yet optimal \(g\) is a spline!
Specifically, a Natural Cubic Spline with…
- Knots at every data point (\(K = N\), \(\xi_i = x_i\)), but
- Penalized via (optimal) \(\lambda^*\), so not as wiggly as “free to wiggle” splines from previous approach: shrunken natural cubic spline
Related (Important!) Local Regression at \(X = x_0\)
Identify \(k\) points closest to \(x_0\)
Compute weights \(K_i = K(x_0, x_i)\), such that \(K_i = 0\) for furthest \(i\), and \(K_i\) increases as \(x_i\) gets closer to \(x_0\)
Compute Weighted Least Squares Estimate
\[ \boldsymbol\beta^*_{\text{WLS}} = \underset{\boldsymbol\beta}{\operatorname{argmin}} \left[ \frac{1}{N}\sum_{i=1}^{N}K_i(\widehat{y}_i(\boldsymbol\beta) - y_i)^2 \right] \]
Estimate is ready! \(\widehat{f}(x_0) = \beta^{\text{WLS}}_0 + \beta^{\text{WLS}}_1 x_0\).
References
DSAN 5300-01 Week 7: Basis Functions and Splines