Week 2: Linear Regression

DSAN 5300: Statistical Learning
Spring 2025, Georgetown University

Jeff Jacobs

jj1088@georgetown.edu

Monday, January 13, 2025

Linear Regression

  • What happens to my dependent variable \(Y\) when my independent variable \(X\) changes by 1 unit?

  • Whenever you carry out a regression, keep the goal in the front of your mind:

    The Goal of Regression

    Find a line \(\widehat{y} = mx + b\) that best predicts \(Y\) for given values of \(X\)

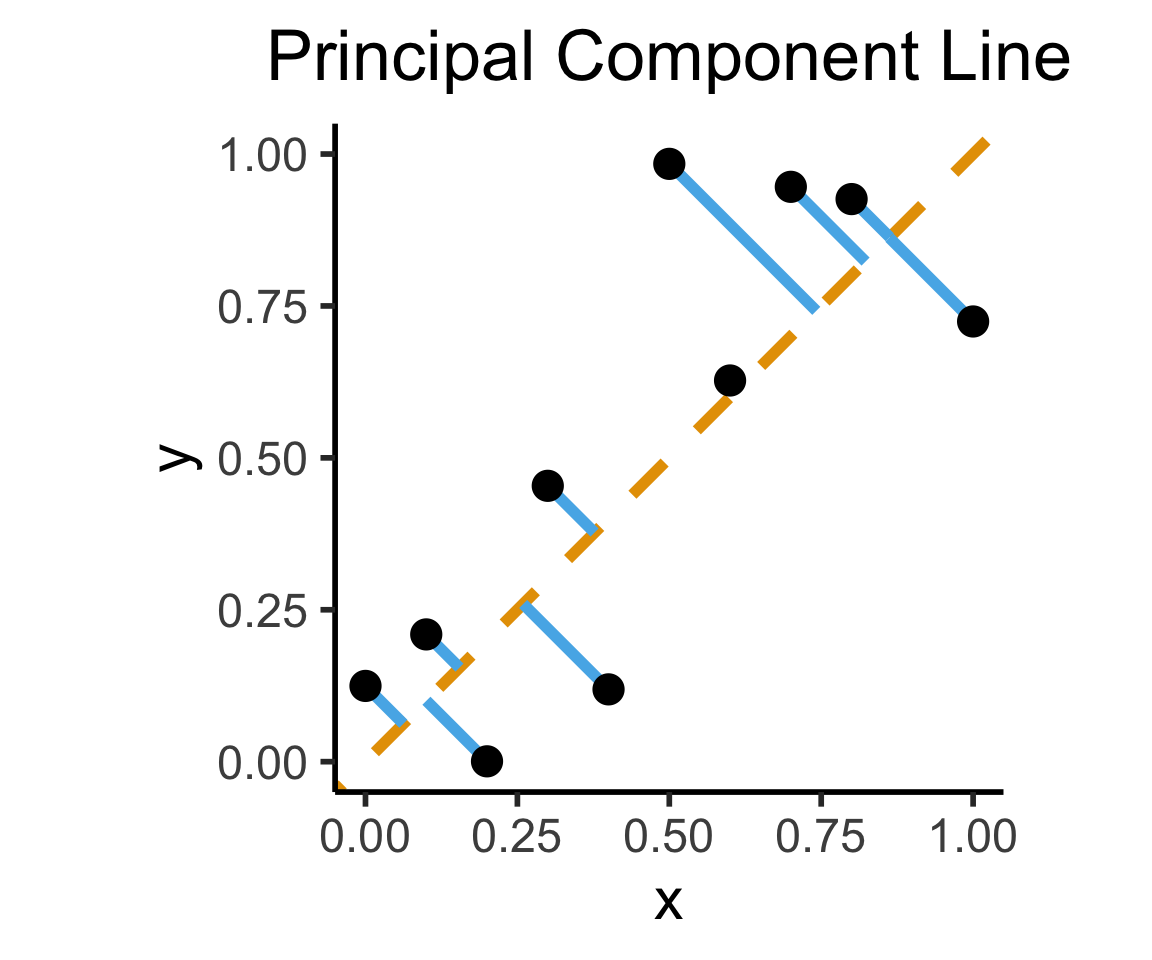
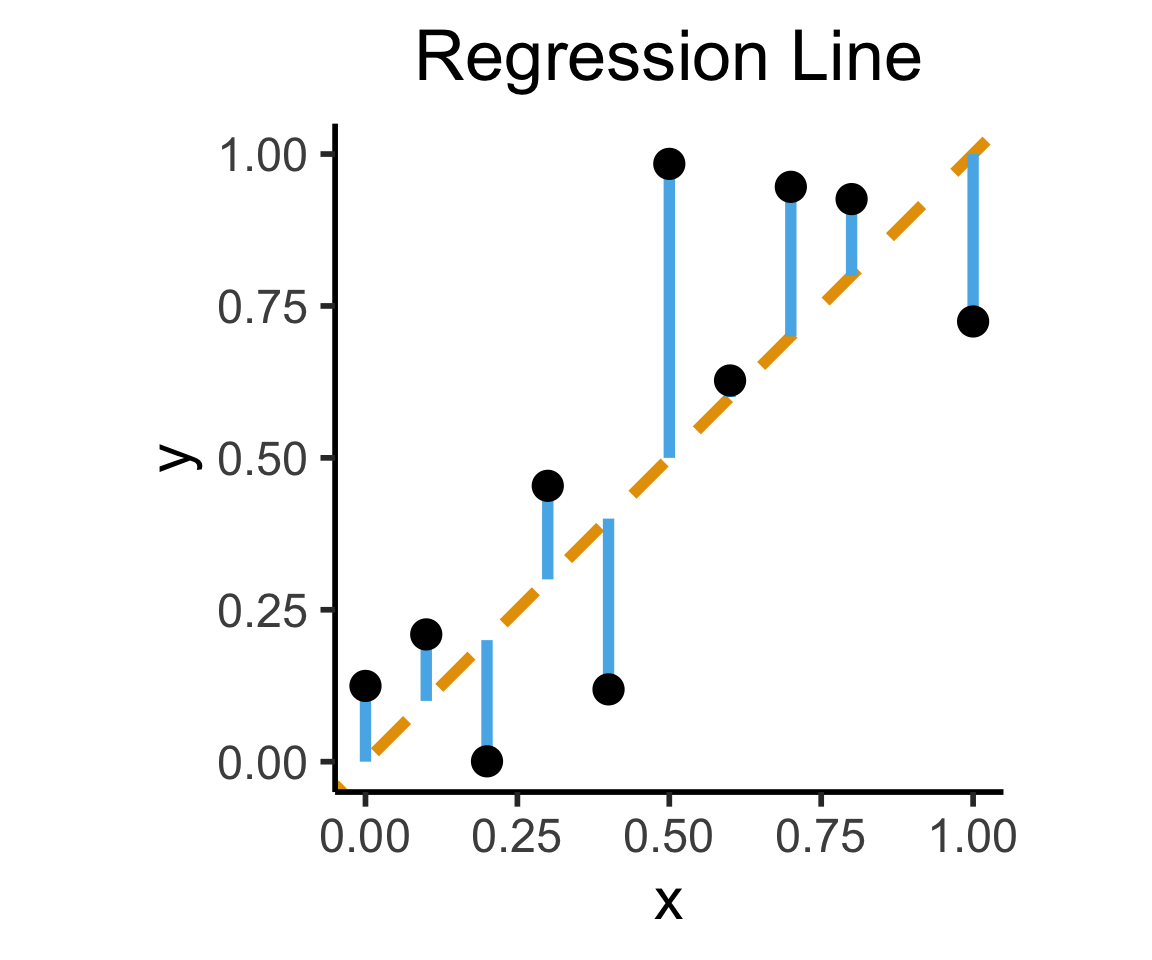
How Do We Define “Best”?

  • Intuitively, two different ways to measure how well a line fits the data:
Code 
library(tidyverse)
set.seed(5321)
N <- 11
x <- seq(from = 0, to = 1, by = 1 / (N - 1))
y <- x + rnorm(N, 0, 0.2)
mean_y <- mean(y)
spread <- y - mean_y
df <- tibble(x = x, y = y, spread = spread)
ggplot(df, aes(x=x, y=y)) +
  geom_abline(slope=1, intercept=0, linetype="dashed", color=cbPalette[1], linewidth=g_linewidth*2) +
  geom_segment(xend=(x+y)/2, yend=(x+y)/2, linewidth=g_linewidth*2, color=cbPalette[2]) +
  geom_point(size=g_pointsize) +
  coord_equal() +
  xlim(0, 1) + ylim(0, 1) +
  dsan_theme("half") +
  labs(
    title = "Principal Component Line"
  )
ggplot(df, aes(x=x, y=y)) +
  geom_abline(slope=1, intercept=0, linetype="dashed", color=cbPalette[1], linewidth=g_linewidth*2) +
  geom_segment(xend=x, yend=x, linewidth=g_linewidth*2, color=cbPalette[2]) +
  geom_point(size=g_pointsize) +
  coord_equal() +
  xlim(0, 1) + ylim(0, 1) +
  dsan_theme("half") +
  labs(
    title = "Regression Line"
  )

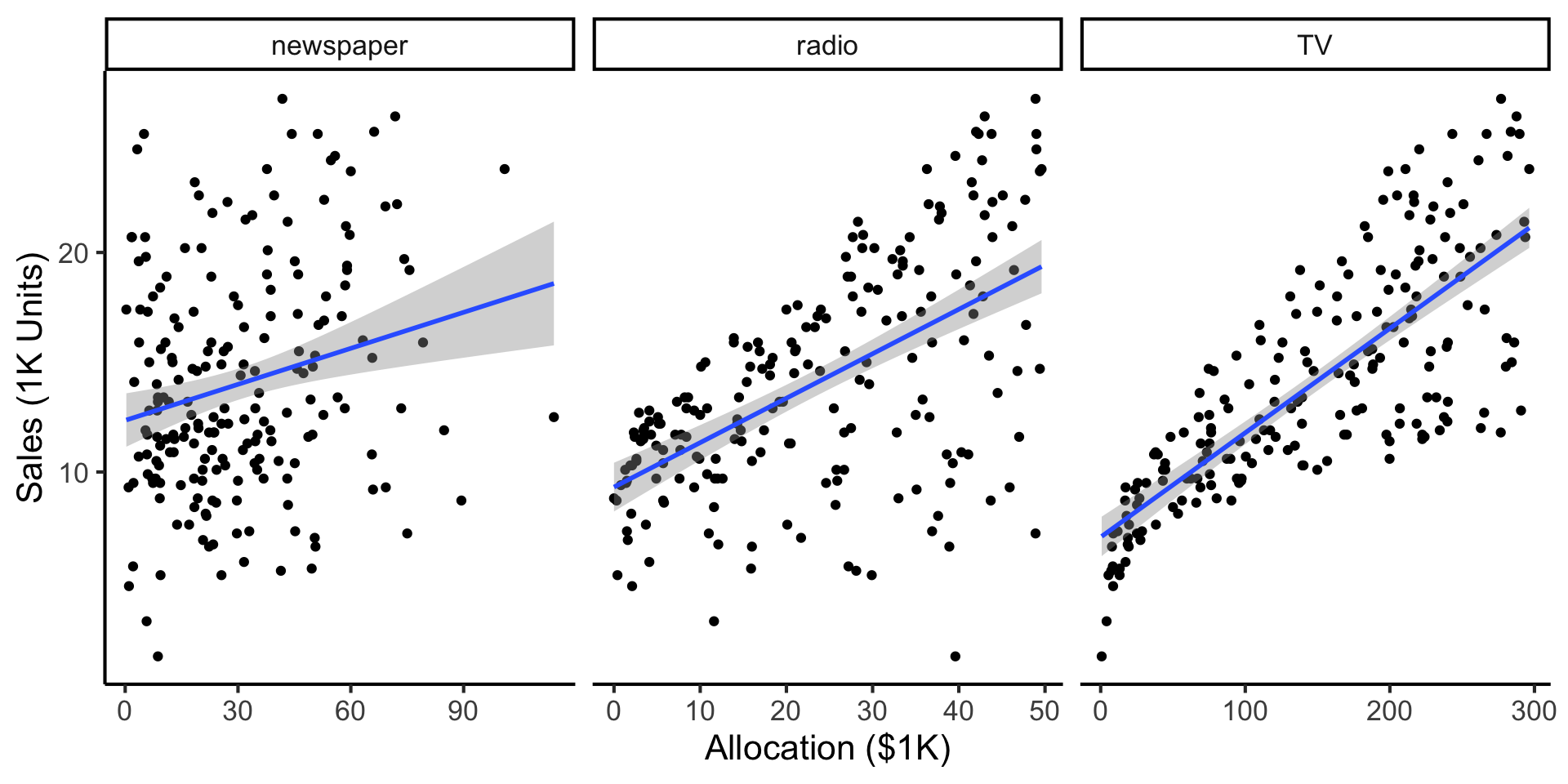
Predictive Example: Advertising Effects

  • Independent variable: $ put into advertisements
  • Dependent variable: Sales
  • Goal: Figure out a good way to allocate an advertising budget
Code 
library(tidyverse)
ad_df <- read_csv("assets/Advertising.csv") |> rename(id=`...1`)
long_df <- ad_df |> pivot_longer(-c(id, sales), names_to="medium", values_to="allocation")
long_df |> ggplot(aes(x=allocation, y=sales)) +
  geom_point() +
  facet_wrap(vars(medium), scales="free_x") +
  geom_smooth(method='lm', formula="y ~ x") +
  theme_dsan() +
  labs(
    x = "Allocation ($1K)",
    y = "Sales (1K Units)"
  )

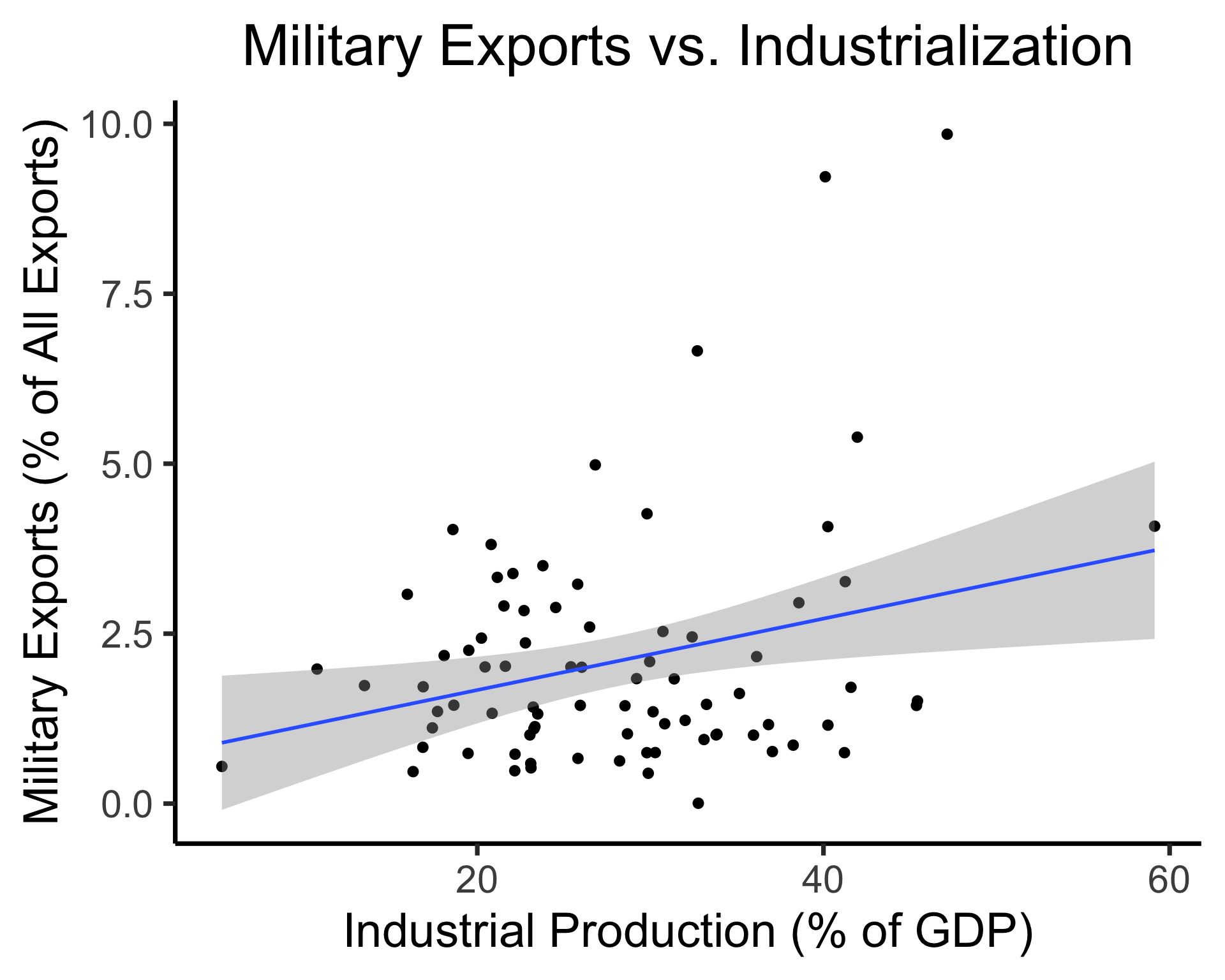
Explanatory Example: Industrialization Effects

Code 
library(tidyverse)
gdp_df <- read_csv("assets/gdp_pca.csv")
mil_plot <- gdp_df |> ggplot(aes(x=industrial, y=military)) +
  geom_point(size=0.5*g_pointsize) +
  geom_smooth(method='lm', formula="y ~ x", linewidth=1) +
  theme_dsan() +
  labs(
    title="Military Exports vs. Industrialization",
    x="Industrial Production (% of GDP)",
    y="Military Exports (% of All Exports)"
  )
mil_plot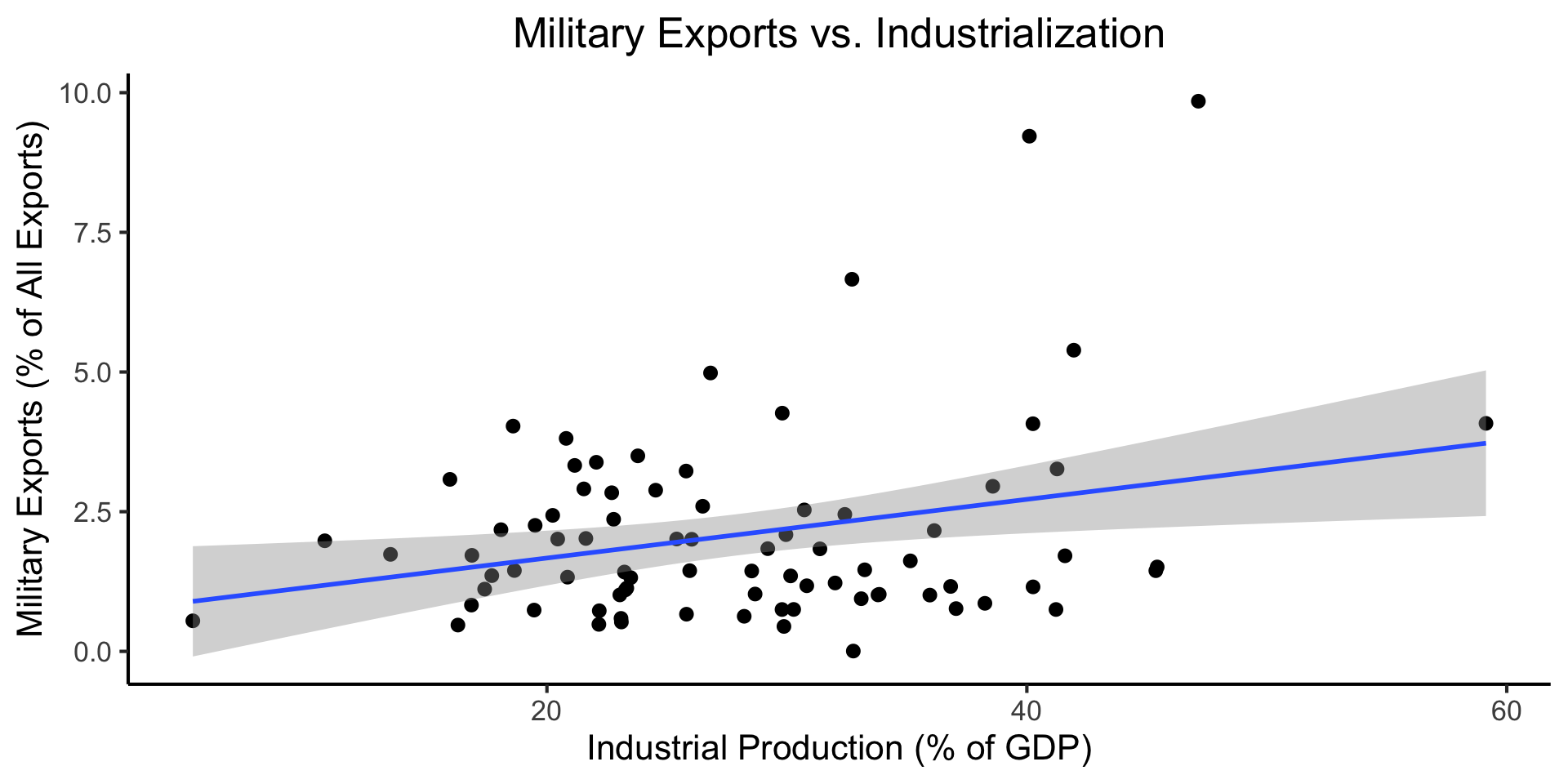

Simple Linear Regression

  • For now, we treat Newspaper, Radio, TV advertising separately: how much do sales increase per $1 into [medium]? (Later we’ll consider them jointly: multiple regression)

  • Our model:

    \[ Y = \underbrace{\param{\beta_0}}_{\mathclap{\text{Intercept}}} + \underbrace{\param{\beta_1}}_{\mathclap{\text{Slope}}}X + \varepsilon \]

  • This model generates predictions via

    \[ \widehat{y} = \underbrace{\widehat{\beta_0}}_{\mathclap{\small\begin{array}{c}\text{Estimated} \\[-5mm] \text{intercept}\end{array}}} ~+~ \underbrace{\widehat{\beta_1}}_{\mathclap{\small\begin{array}{c}\text{Estimated} \\[-4mm] \text{slope}\end{array}}}\cdot x \]

  • Note how these predictions will be wrong (unless the data is perfectly linear)

  • We’ve accounted for this in our model (by including \(\varepsilon\) term)!

  • But, we’d like to find estimates \(\widehat{\beta}_0\) and \(\widehat{\beta}_1\) that produce the “least wrong” predictions: motivates focus on residuals…

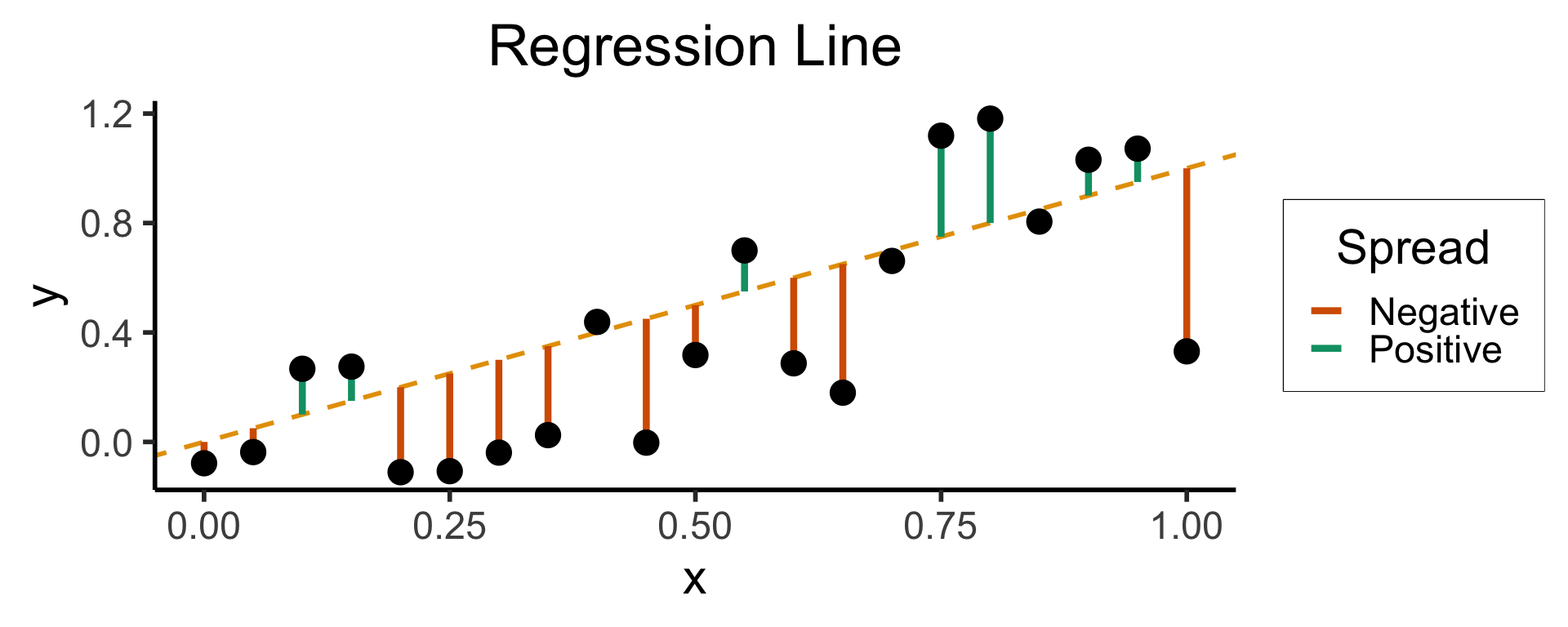
Least Squares: Minimizing Residuals

What can we optimize to ensure these residuals are as small as possible?

Code 
N <- 21
x <- seq(from = 0, to = 1, by = 1 / (N - 1))
y <- x + rnorm(N, 0, 0.25)
mean_y <- mean(y)
spread <- y - mean_y
sim_lg_df <- tibble(x = x, y = y, spread = spread)
sim_lg_df |> ggplot(aes(x=x, y=y)) +
  geom_abline(slope=1, intercept=0, linetype="dashed", color=cbPalette[1], linewidth=g_linewidth) +
  # geom_segment(xend=x, yend=x, linewidth=g_linewidth*2, color=cbPalette[2]) +
  geom_segment(aes(xend=x, yend=x, color=ifelse(y>x,"Positive","Negative")), linewidth=1.5*g_linewidth) +
  geom_point(size=g_pointsize) +
  # coord_equal() +
  theme_dsan("half") +
  scale_color_manual("Spread", values=c("Positive"=cbPalette[3],"Negative"=cbPalette[6]), labels=c("Positive"="Positive","Negative"="Negative")) +
  labs(
    title = "Regression Line"
  )

  • Sum?
Code 
large_sum <- sum(sim_lg_df$spread)
writeLines(fmt_decimal(large_sum))
0.0000000000
  • Sum of Squares?
Code 
large_sqsum <- sum((sim_lg_df$spread)^2)
writeLines(fmt_decimal(large_sqsum))
3.8405017200
Code 
N <- 21
x <- seq(from = 0, to = 1, by = 1 / (N - 1))
y <- x + rnorm(N, 0, 0.05)
mean_y <- mean(y)
spread <- y - mean_y
sim_sm_df <- tibble(x = x, y = y, spread = spread)
sim_sm_df |> ggplot(aes(x=x, y=y)) +
  geom_abline(slope=1, intercept=0, linetype="dashed", color=cbPalette[1], linewidth=g_linewidth) +
  # geom_segment(xend=x, yend=x, linewidth=g_linewidth*2, color=cbPalette[2]) +
  geom_segment(aes(xend=x, yend=x, color=ifelse(y>x,"Positive","Negative")), linewidth=1.5*g_linewidth) +
  geom_point(size=g_pointsize) +
  # coord_equal() +
  theme_dsan("half") +
  scale_color_manual("Spread", values=c("Positive"=cbPalette[3],"Negative"=cbPalette[6]), labels=c("Positive"="Positive","Negative"="Negative")) +
  labs(
    title = "Regression Line"
  )

  • Sum?
Code 
small_rsum <- sum(sim_sm_df$spread)
writeLines(fmt_decimal(small_rsum))
0.0000000000
  • Sum of Squares?
Code 
small_sqrsum <- sum((sim_sm_df$spread)^2)
writeLines(fmt_decimal(small_sqrsum))
1.9748635217

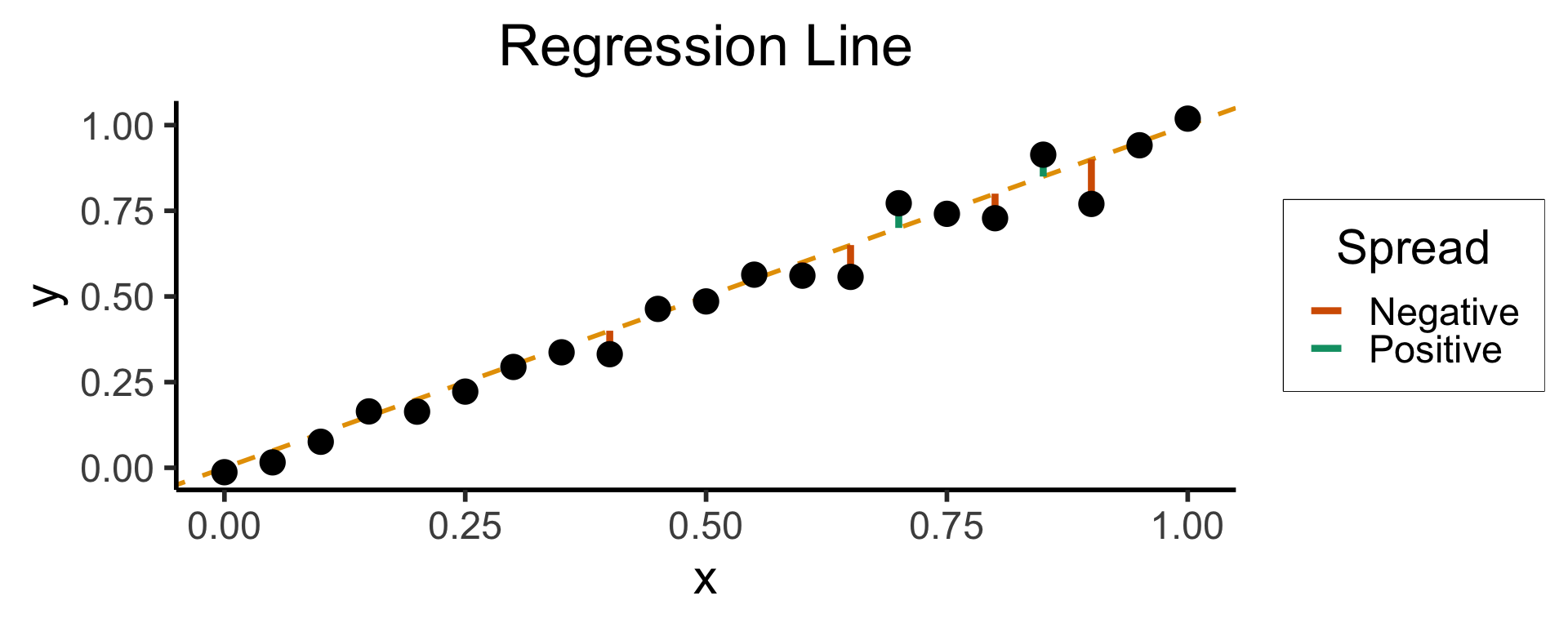
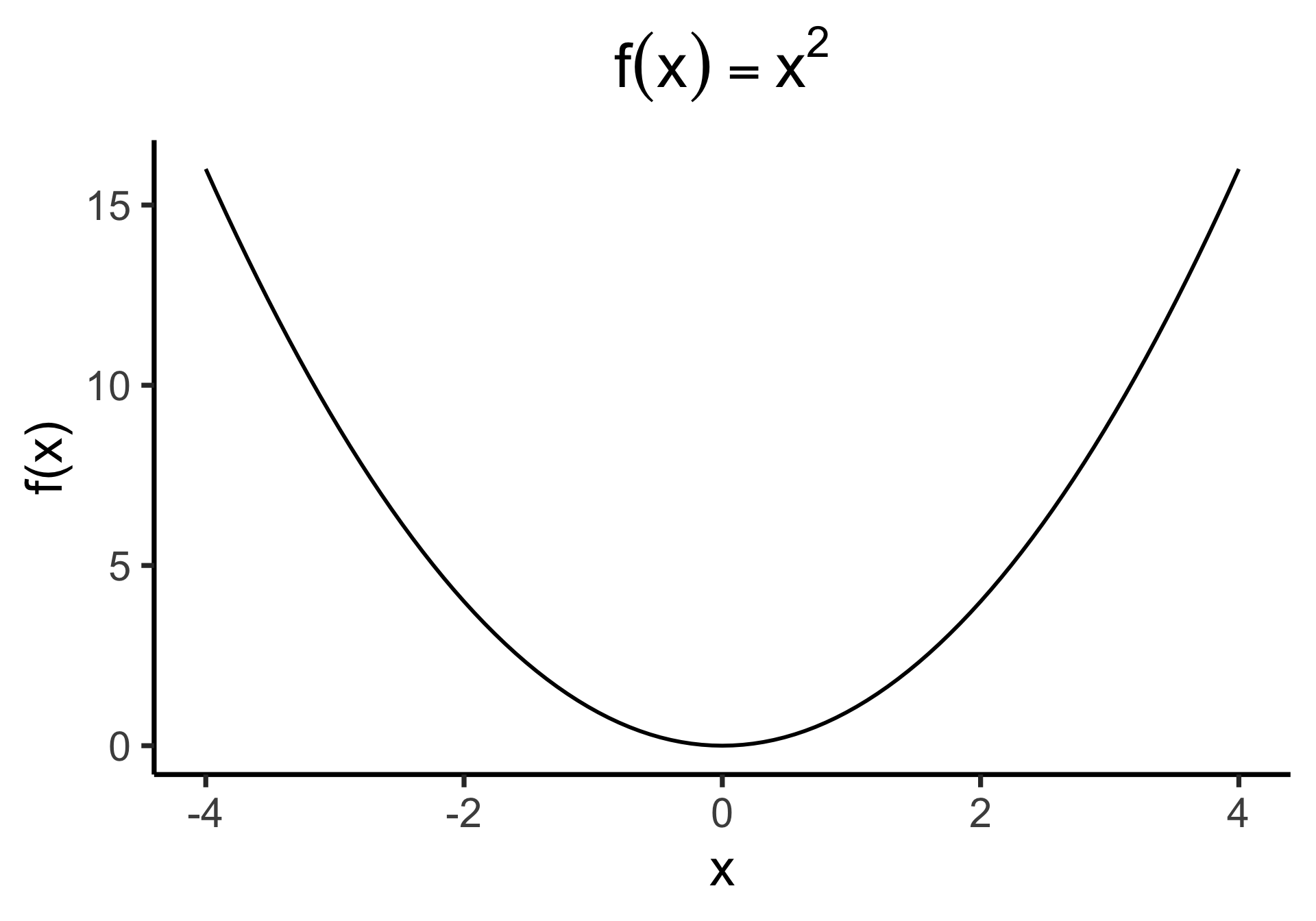
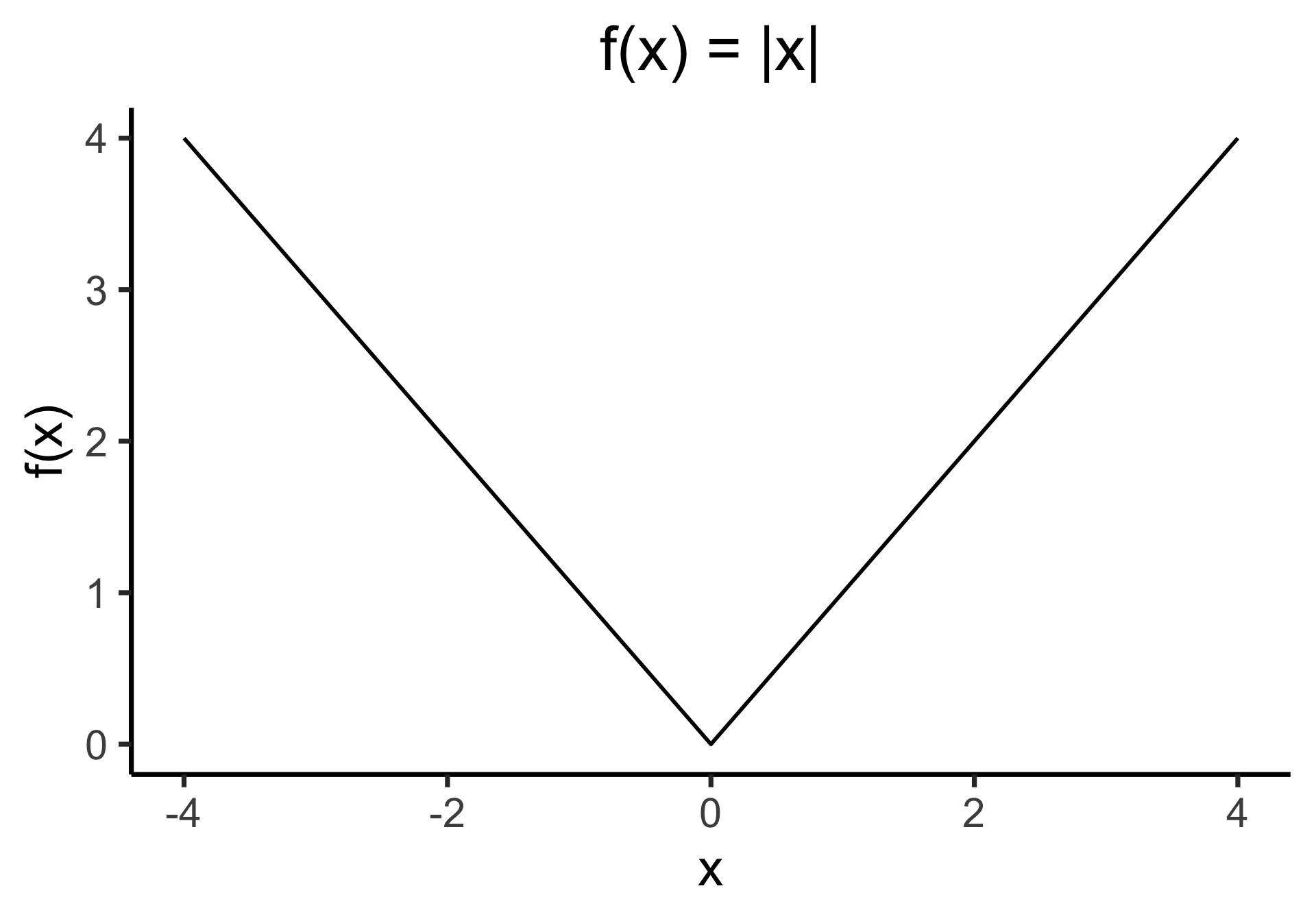
Why Not Absolute Value?

  • Two feasible ways to prevent positive and negative residuals cancelling out:
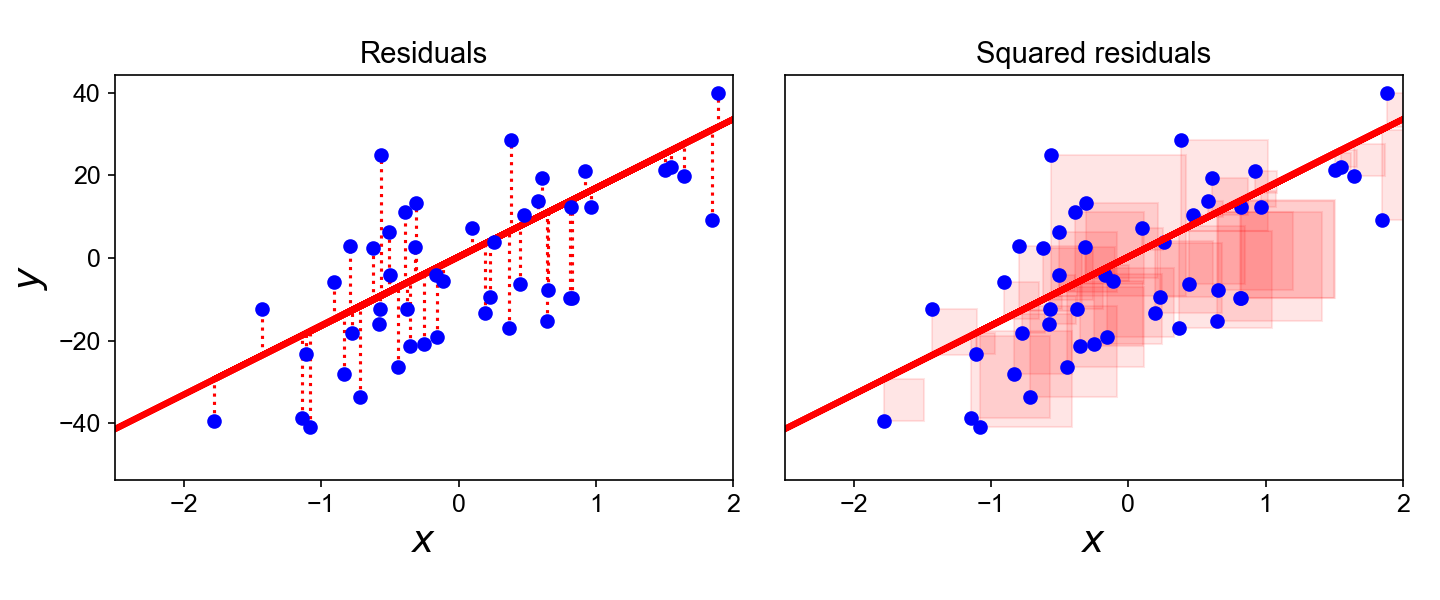
    • Absolute value \(\left|y - \widehat{y}\right|\) or squaring \(\left( y - \widehat{y} \right)^2\)
  • But remember that we’re aiming to minimize these residuals…
  • Ghost of calculus past 😱: which is differentiable everywhere?
Code 
library(latex2exp)
x2_label <- latex2exp("$f(x) = x^2$")
ggplot(data.frame(x=c(-4,4)), aes(x=x)) +
  stat_function(fun=~ .x^2, linewidth = g_linewidth) +
  dsan_theme("quarter") +
  labs(
    title=x2_label,
    y="f(x)"
  )

Code 
# Could use facet_grid() here, but it doesn't work too nicely with stat_function() :(
ggplot(data.frame(x=c(-4,4)), aes(x=x)) +
  stat_function(fun=~ abs(.x), linewidth=g_linewidth) +
  dsan_theme("quarter") +
  labs(
    title="f(x) = |x|",
    y="f(x)"
  )

Outliers Penalized Quadratically

Image Source

Key Features of Regression Line

  • Regression line is BLUE: Best Linear Unbiased Estimator
  • What exactly is it the “best” linear estimator of?

\[ \widehat{y} = \underbrace{\widehat{\beta}_0}_{\mathclap{\small\begin{array}{c}\text{Estimated} \\[-5mm] \text{intercept}\end{array}}} ~+~ \underbrace{\widehat{\beta}_1}_{\mathclap{\small\begin{array}{c}\text{Estimated} \\[-4mm] \text{slope}\end{array}}}\cdot x \]

is chosen so that

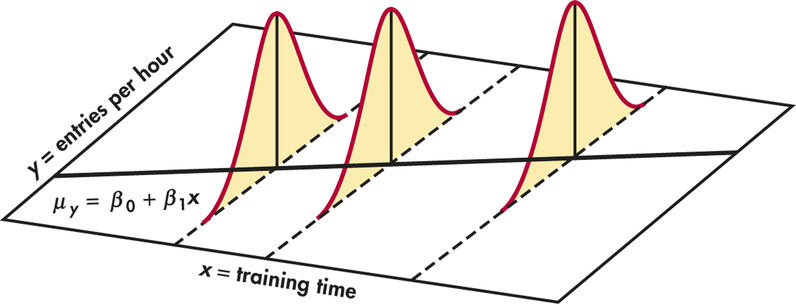
\[ \widehat{\theta} = \left(\widehat{\beta}_0, \widehat{\beta}_1\right) = \argmin_{\beta_0, \beta_1}\left[ \sum_{x_i \in X} \left(~~\overbrace{\widehat{y}(x_i)}^{\mathclap{\small\text{Predicted }y}} - \overbrace{\expect{Y \mid X = x_i}}^{\small \text{Avg. }y\text{ when }x = x_i}\right)^{2~} \right] \]

Where Did That \(\mathbb{E}[Y \mid X = x_i]\) Come From?

Image Source

But… What About All the Other Types of Vars?

  • 5000: you saw, e.g., nominal, ordinal, cardinal vars
  • 5100: you wrestled with discrete vs. continuous RVs
  • Good News #1: Regression can handle all these types+more!
  • Good News #2: Distinctions between classification and regression start to diminish as you learn fancier regression methods! (One key tool here: link functions)
  • By end of 5300 you should have something on your toolbelt for handling most cases like “I want to do [regression / classification], but my data is [not cardinal+continuous]”

Deriving the Least Squares Estimate

A Sketch (HW is the Full Thing)

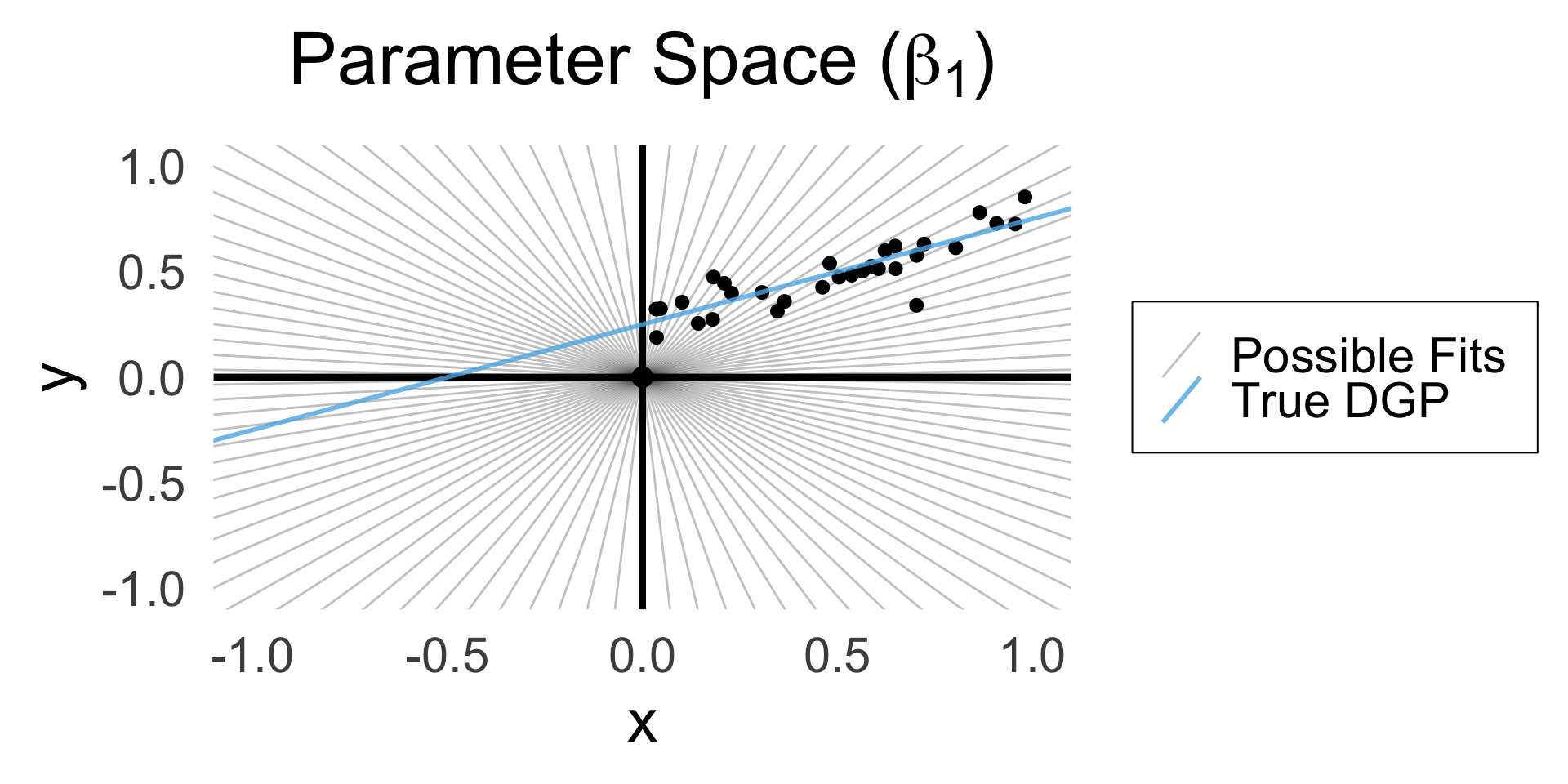
  • OLS for regression without intercept \(\param{\beta_0}\): Which line through origin best predicts \(Y\)?
  • (Good practice + reminder of how restricted linear models are!)

\[ Y = \beta_1 X + \varepsilon \]

Code 
library(latex2exp)
set.seed(5300)
# rand_slope <- log(runif(80, min=0, max=1))
# rand_slope[41:80] <- -rand_slope[41:80]
# rand_lines <- tibble::tibble(
#   id=1:80, slope=rand_slope, intercept=0
# )
# angles <- runif(100, -pi/2, pi/2)
angles <- seq(from=-pi/2, to=pi/2, length.out=50)
possible_lines <- tibble::tibble(
  slope=tan(angles), intercept=0
)
num_points <- 30
x_vals <- runif(num_points, 0, 1)
y0_vals <- 0.5 * x_vals + 0.25
y_noise <- rnorm(num_points, 0, 0.07)
y_vals <- y0_vals + y_noise
rand_df <- tibble::tibble(x=x_vals, y=y_vals)
title_exp <- latex2exp("Parameter Space ($\\beta_1$)")
# Main plot object
gen_lines_plot <- function(point_size=2.5) {
  lines_plot <- rand_df |> ggplot(aes(x=x, y=y)) +
    geom_point(size=point_size) +
    geom_hline(yintercept=0, linewidth=1.5) +
    geom_vline(xintercept=0, linewidth=1.5) +
    # Point at origin
    geom_point(data=data.frame(x=0, y=0), aes(x=x, y=y), size=4) +
    xlim(-1,1) +
    ylim(-1,1) +
    # coord_fixed() +
    theme_dsan_min(base_size=28)
  return(lines_plot)
}
main_lines_plot <- gen_lines_plot()
main_lines_plot +
  # Parameter space of possible lines
  geom_abline(
    data=possible_lines,
    aes(slope=slope, intercept=intercept, color='possible'),
    # linetype="dotted",
    # linewidth=0.75,
    alpha=0.25
  ) +
  # True DGP
  geom_abline(
    aes(
      slope=0.5,
      intercept=0.25,
      color='true'
    ), linewidth=1, alpha=0.8
  ) + 
  scale_color_manual(
    element_blank(),
    values=c('possible'="black", 'true'=cb_palette[2]),
    labels=c('possible'="Possible Fits", 'true'="True DGP")
  ) +
  remove_legend_title() +
  labs(
    title=title_exp
  )

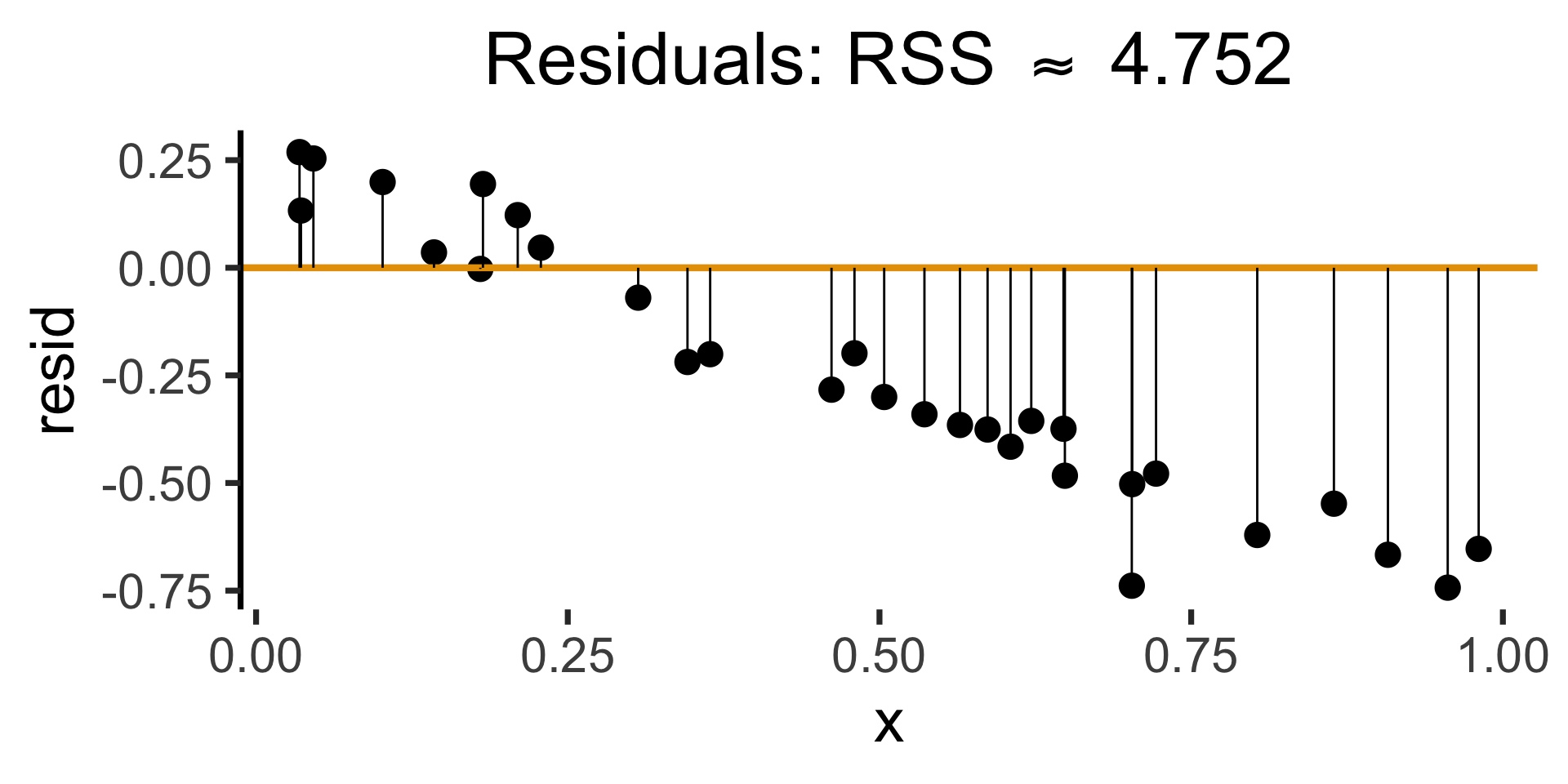
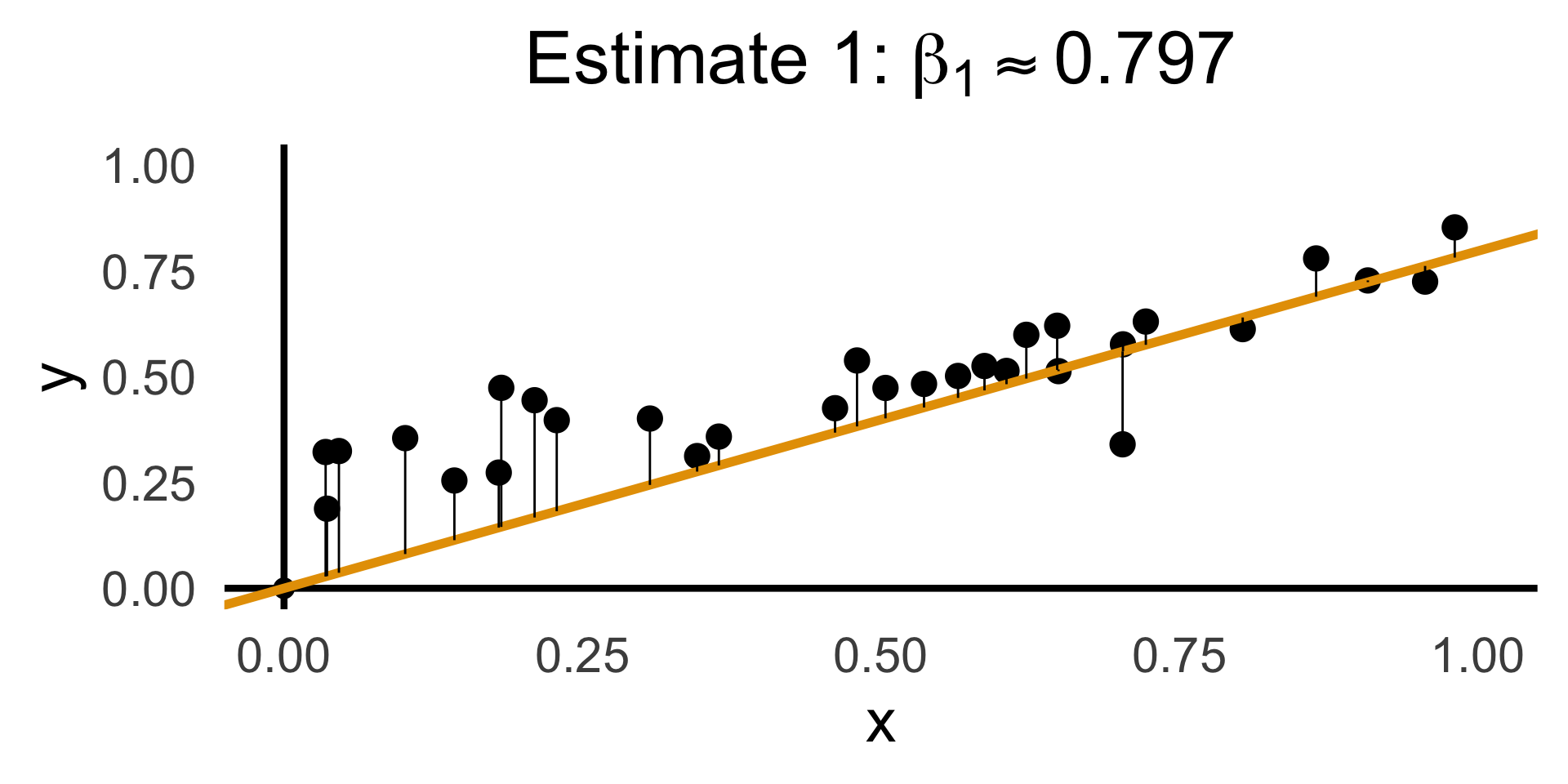
Evaluating with Residuals

Code 
rc1_df <- possible_lines |> slice(n() - 14)
# Predictions for this choice
rc1_pred_df <- rand_df |> mutate(
  y_pred = rc1_df$slope * x,
  resid = y - y_pred
)
rc1_label <- latex2exp(paste0("Estimate 1: $\\beta_1 \\approx ",round(rc1_df$slope, 3),"$"))
rc1_lines_plot <- gen_lines_plot(point_size=5)
rc1_lines_plot +
  geom_abline(
    data=rc1_df,
    aes(intercept=intercept, slope=slope),
    linewidth=2,
    color=cb_palette[1]
  ) +
  geom_segment(
    data=rc1_pred_df,
    aes(x=x, y=y, xend=x, yend=y_pred),
    # color=cb_palette[1]
  ) +
  xlim(0, 1) + ylim(0, 1) +
  labs(
    title = rc1_label
  )

Code 
gen_resid_plot <- function(pred_df) {
  rc_rss <- sum((pred_df$resid)^2)
  rc_resid_label <- latex2exp(paste0("Residuals: RSS $\\approx$ ",round(rc_rss,3)))
  rc_resid_plot <- pred_df |> ggplot(aes(x=x, y=resid)) +
    geom_point(size=5) +
    geom_hline(
      yintercept=0,
      color=cb_palette[1],
      linewidth=1.5
    ) +
    geom_segment(
      aes(xend=x, yend=0)
    ) +
    theme_dsan(base_size=28) +
    theme(axis.line.x = element_blank()) +
    labs(
      title=rc_resid_label
    )
  return(rc_resid_plot)
}
rc1_resid_plot <- gen_resid_plot(rc1_pred_df)
rc1_resid_plot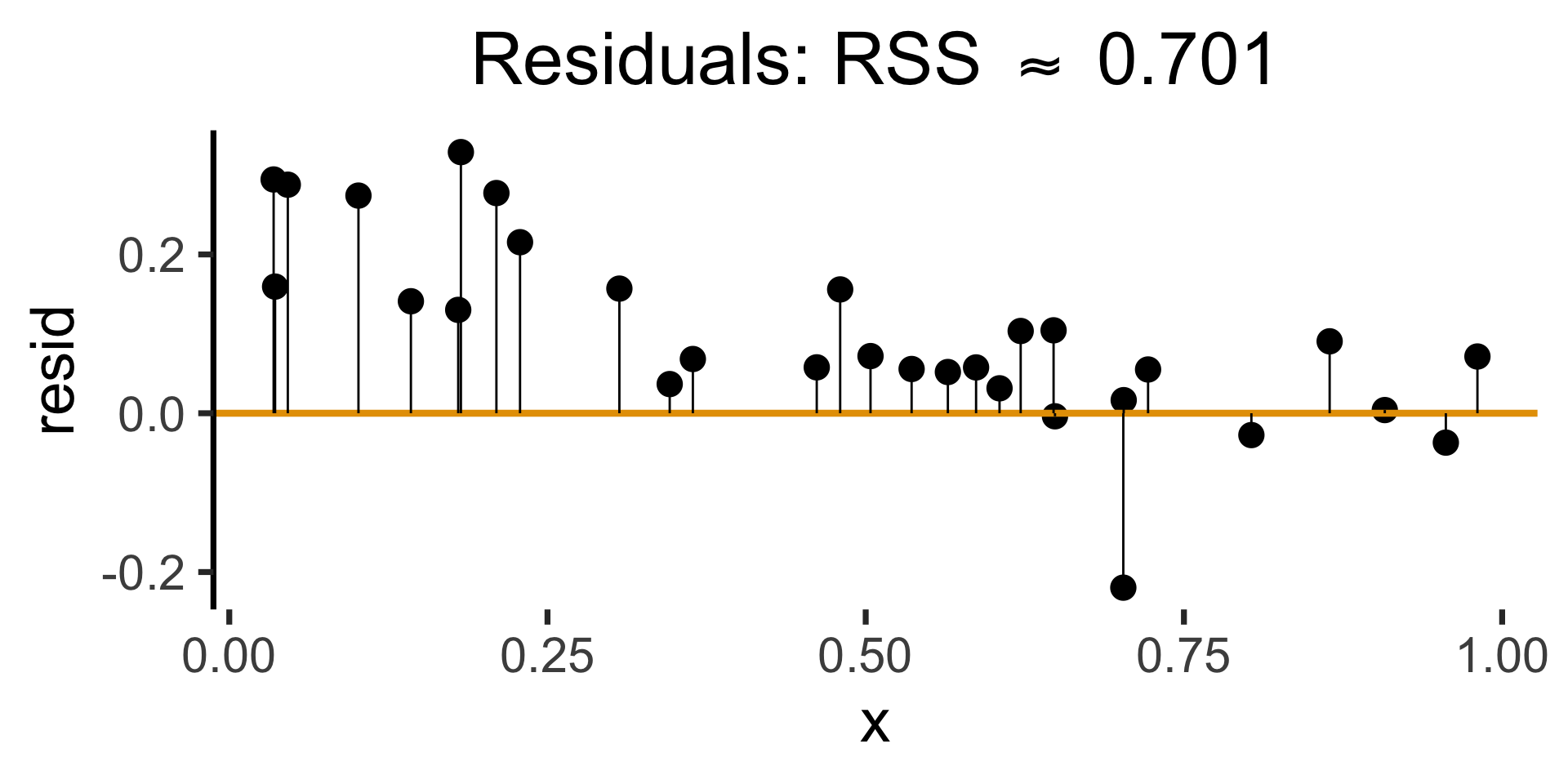

Code 
rc2_df <- possible_lines |> slice(n() - 9)
# Predictions for this choice
rc2_pred_df <- rand_df |> mutate(
  y_pred = rc2_df$slope * x,
  resid = y - y_pred
)
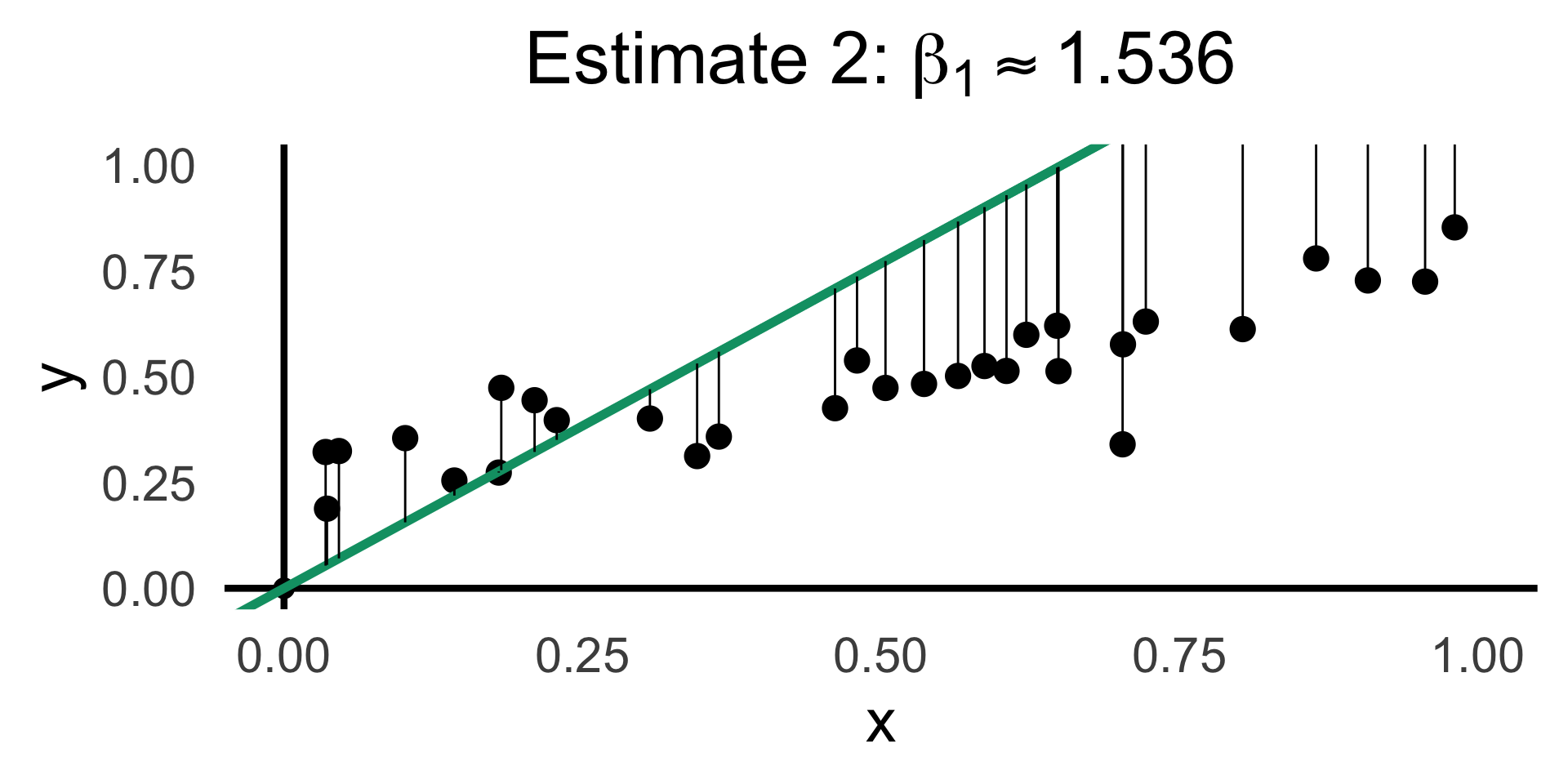
rc2_label <- latex2exp(paste0("Estimate 2: $\\beta_1 \\approx ",round(rc2_df$slope,3),"$"))
rc2_lines_plot <- gen_lines_plot(point_size=5)
rc2_lines_plot +
  geom_abline(
    data=rc2_df,
    aes(intercept=intercept, slope=slope),
    linewidth=2,
    color=cb_palette[3]
  ) +
  geom_segment(
    data=rc2_pred_df,
    aes(
      x=x, y=y, xend=x,
      yend=ifelse(y_pred <= 1, y_pred, Inf)
    )
    # color=cb_palette[1]
  ) +
  xlim(0, 1) + ylim(0, 1) +
  labs(
    title=rc2_label
  )

Code 
rc2_resid_plot <- gen_resid_plot(rc2_pred_df)
rc2_resid_plot

Now the Math

\[ \begin{align*} \beta_1^* = \argmin_{\beta_1}\left[ \sum_{i=1}^{n}(\widehat{y}_i - y_i)^2 \right] = \argmin_{\beta_1}\left[ \sum_{i=1}^{n}(\beta_1x_i - y_i)^2 \right] \end{align*} \]

We can compute this derivative to obtain:

\[ \frac{\partial}{\partial\beta_1}\left[ \sum_{i=1}^{n}(\beta_1x_i - y_i)^2 \right] = \sum_{i=1}^{n}\frac{\partial}{\partial\beta_1}(\beta_1x_i - y_i)^2 = \sum_{i=1}^{n}2(\beta_1x_i - y_i)x_i \]

And our first-order condition means that:

\[ \sum_{i=1}^{n}2(\beta_1^*x_i - y_i)x_i = 0 \iff \beta_1^*\sum_{i=1}^{n}x_i^2 = \sum_{i=1}^{n}x_iy_i \iff \boxed{\beta_1^* = \frac{\sum_{i=1}^{n}x_iy_i}{\sum_{i=1}^{n}x_i^2}} \]

Doing Things With Regression

Regression: R vs. statsmodels

In (Base) R: lm()
Code 
lin_model <- lm(sales ~ TV, data=ad_df)
summary(lin_model)

Call:
lm(formula = sales ~ TV, data = ad_df)

Residuals:
    Min      1Q  Median      3Q     Max 
-8.3860 -1.9545 -0.1913  2.0671  7.2124 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 7.032594   0.457843   15.36   <2e-16 ***
TV          0.047537   0.002691   17.67   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.259 on 198 degrees of freedom
Multiple R-squared:  0.6119,    Adjusted R-squared:  0.6099 
F-statistic: 312.1 on 1 and 198 DF,  p-value: < 2.2e-16

General syntax:

lm(
  dependent ~ independent + controls,
  data = my_df
)
In Python: smf.ols()
Code 
import statsmodels.formula.api as smf
results = smf.ols("sales ~ TV", data=ad_df).fit()
print(results.summary(slim=True))
                            OLS Regression Results                            
==============================================================================
Dep. Variable:                  sales   R-squared:                       0.612
Model:                            OLS   Adj. R-squared:                  0.610
No. Observations:                 200   F-statistic:                     312.1
Covariance Type:            nonrobust   Prob (F-statistic):           1.47e-42
==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
Intercept      7.0326      0.458     15.360      0.000       6.130       7.935
TV             0.0475      0.003     17.668      0.000       0.042       0.053
==============================================================================

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

General syntax:

smf.ols(
  "dependent ~ independent + controls",
  data = my_df
)

Interpreting Output

Code 
mil_plot + theme_dsan("quarter")

Code 
gdp_model <- lm(military ~ industrial, data=gdp_df)
summary(gdp_model)

Call:
lm(formula = military ~ industrial, data = gdp_df)

Residuals:
    Min      1Q  Median      3Q     Max 
-2.3354 -1.0997 -0.3870  0.6081  6.7508 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)  
(Intercept)  0.61969    0.59526   1.041   0.3010  
industrial   0.05253    0.02019   2.602   0.0111 *
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.671 on 79 degrees of freedom
  (8 observations deleted due to missingness)
Multiple R-squared:  0.07895,   Adjusted R-squared:  0.06729 
F-statistic: 6.771 on 1 and 79 DF,  p-value: 0.01106

Zooming In: Coefficients

Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.61969 0.59526 1.041 0.3010
industrial 0.05253 0.02019 2.602 0.0111 *
\(\widehat{\beta}\) Uncertainty Test stat \(t\) How extreme is \(t\)? Signif. Level

\[ \widehat{y} \approx \class{cb1}{\overset{\beta_0}{\underset{\small \pm 0.595}{0.620}}} + \class{cb2}{\overset{\beta_1}{\underset{\small \pm 0.020}{0.053}}} \cdot x \]

Zooming In: Significance

Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.61969 0.59526 1.041 0.3010
industrial 0.05253 0.02019 2.602 0.0111 *
\(\widehat{\beta}\) Uncertainty Test stat \(t\) How extreme is \(t\)? Signif. Level
Code 
library(ggplot2)
int_tstat <- 1.041
int_tstat_str <- sprintf("%.02f", int_tstat)
label_df_int <- tribble(
    ~x, ~y, ~label,
    0.25, 0.05, paste0("P(t > ",int_tstat_str,")\n= 0.3")
)
label_df_signif_int <- tribble(
    ~x, ~y, ~label,
    2.7, 0.075, "95% Signif.\nCutoff"
)
funcShaded <- function(x, lower_bound, upper_bound){
    y <- dnorm(x)
    y[x < lower_bound | x > upper_bound] <- NA
    return(y)
}
funcShadedIntercept <- function(x) funcShaded(x, int_tstat, Inf)
funcShadedSignif <- function(x) funcShaded(x, 1.96, Inf)
ggplot(data=data.frame(x=c(-3,3)), aes(x=x)) +
  stat_function(fun=dnorm, linewidth=g_linewidth) +
  geom_vline(aes(xintercept=int_tstat), linewidth=g_linewidth, linetype="dashed") +
  geom_vline(aes(xintercept = 1.96), linewidth=g_linewidth, linetype="solid") +
  stat_function(fun = funcShadedIntercept, geom = "area", fill = cbPalette[1], alpha = 0.5) +
  stat_function(fun = funcShadedSignif, geom = "area", fill = "grey", alpha = 0.333) +
  geom_text(label_df_int, mapping = aes(x = x, y = y, label = label), size = 10) +
  geom_text(label_df_signif_int, mapping = aes(x = x, y = y, label = label), size = 8) +
  # Add single additional tick
  scale_x_continuous(breaks=c(-2, 0, int_tstat, 2), labels=c("-2","0",int_tstat_str,"2")) +
  dsan_theme("quarter") +
  labs(
    title = "t Value for Intercept",
    x = "t",
    y = "Density"
  ) +
  theme(axis.text.x = element_text(colour = c("black", "black", cbPalette[1], "black")))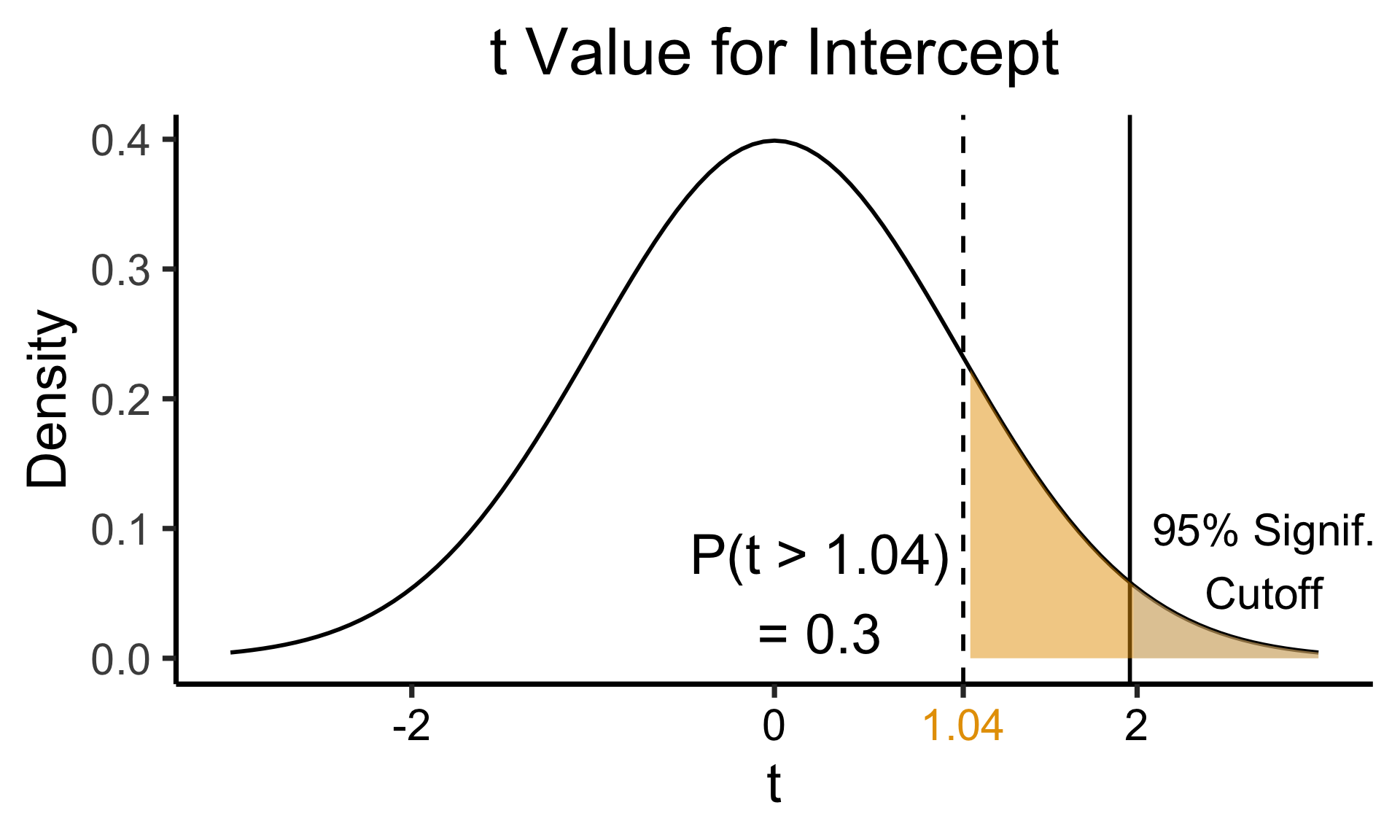

Code 
library(ggplot2)
coef_tstat <- 2.602
coef_tstat_str <- sprintf("%.02f", coef_tstat)
label_df_coef <- tribble(
    ~x, ~y, ~label,
    3.65, 0.06, paste0("P(t > ",coef_tstat_str,")\n= 0.01")
)
label_df_signif_coef <- tribble(
  ~x, ~y, ~label,
  1.05, 0.03, "95% Signif.\nCutoff"
)
funcShadedCoef <- function(x) funcShaded(x, coef_tstat, Inf)
ggplot(data=data.frame(x=c(-4,4)), aes(x=x)) +
  stat_function(fun=dnorm, linewidth=g_linewidth) +
  geom_vline(aes(xintercept=coef_tstat), linetype="dashed", linewidth=g_linewidth) +
  geom_vline(aes(xintercept=1.96), linetype="solid", linewidth=g_linewidth) +
  stat_function(fun = funcShadedCoef, geom = "area", fill = cbPalette[2], alpha = 0.5) +
  stat_function(fun = funcShadedSignif, geom = "area", fill = "grey", alpha = 0.333) +
  # Label shaded area
  geom_text(label_df_coef, mapping = aes(x = x, y = y, label = label), size = 10) +
  # Label significance cutoff
  geom_text(label_df_signif_coef, mapping = aes(x = x, y = y, label = label), size = 8) +
  coord_cartesian(clip = "off") +
  # Add single additional tick
  scale_x_continuous(breaks=c(-4, -2, 0, 2, coef_tstat, 4), labels=c("-4", "-2","0", "2", coef_tstat_str,"4")) +
  dsan_theme("quarter") +
  labs(
    title = "t Value for Coefficient",
    x = "t",
    y = "Density"
  ) +
  theme(axis.text.x = element_text(colour = c("black", "black", "black", "black", cbPalette[2], "black")))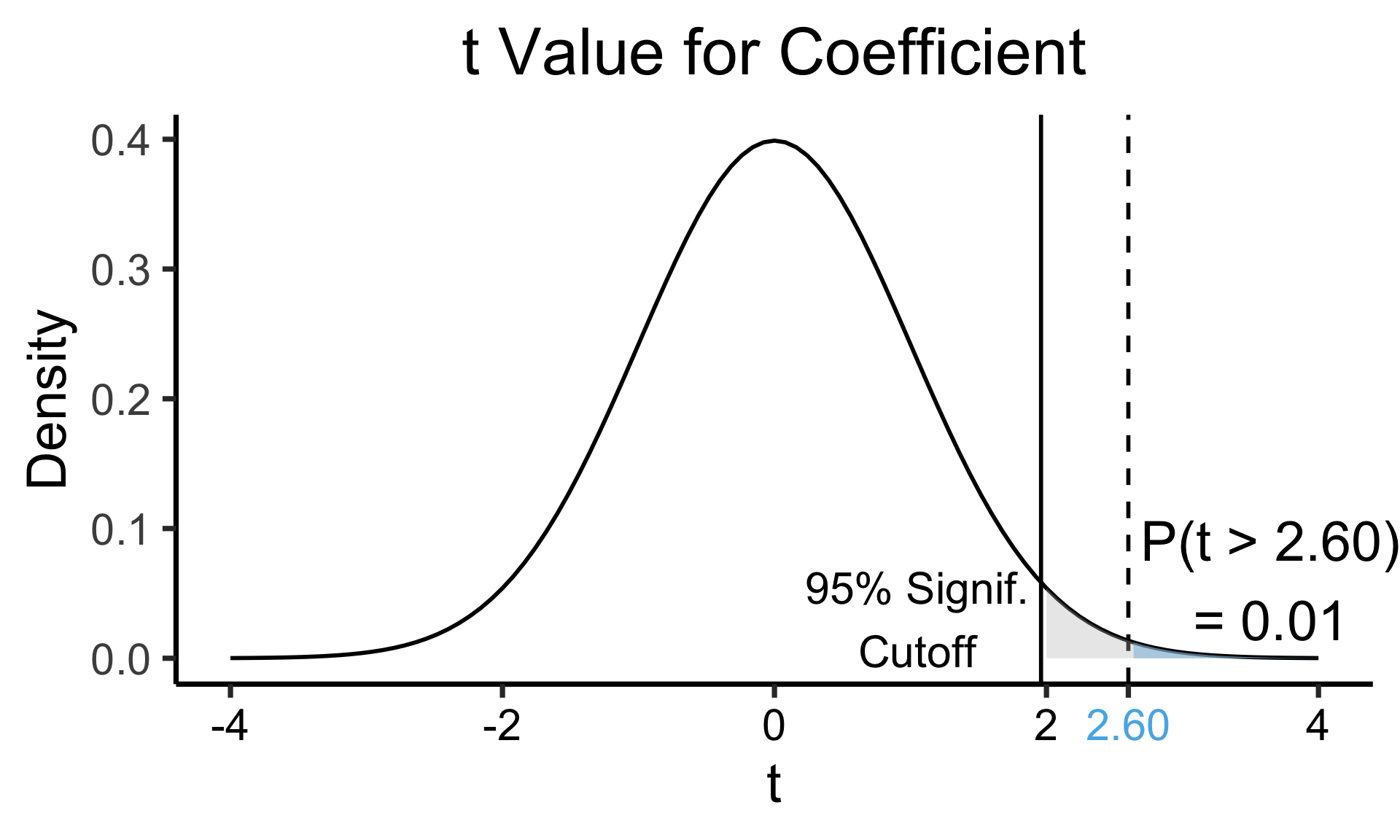

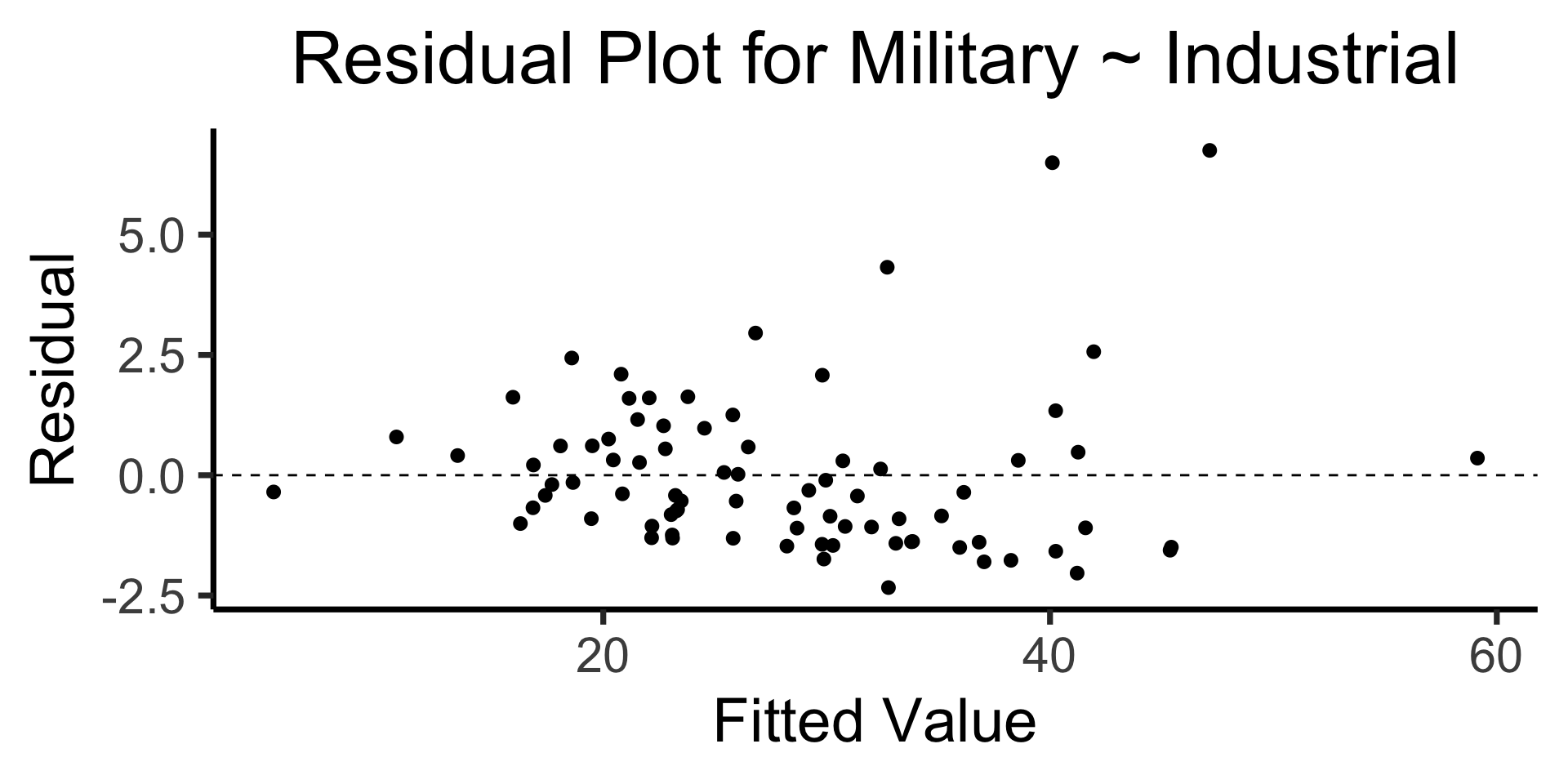
The Residual Plot

  • A key assumption required for OLS: “homoskedasticity”
  • Given our model \[ y_i = \beta_0 + \beta_1x_i + \varepsilon_i \] the errors \(\varepsilon_i\) should not vary systematically with \(i\)
  • Formally: \(\forall i \left[ \Var{\varepsilon_i} = \sigma^2 \right]\)
Code 
library(broom)
gdp_resid_df <- augment(gdp_model)
ggplot(gdp_resid_df, aes(x = industrial, y = .resid)) +
    geom_point(size = g_pointsize/2) +
    geom_hline(yintercept=0, linetype="dashed") +
    dsan_theme("quarter") +
    labs(
      title = "Residual Plot for Military ~ Industrial",
      x = "Fitted Value",
      y = "Residual"
    )

Code 
x <- 1:80
errors <- rnorm(length(x), 0, x^2/1000)
y <- x + errors
het_model <- lm(y ~ x)
df_het <- augment(het_model)
ggplot(df_het, aes(x = .fitted, y = .resid)) +
    geom_point(size = g_pointsize / 2) +
    geom_hline(yintercept = 0, linetype = "dashed") +
    dsan_theme("quarter") +
    labs(
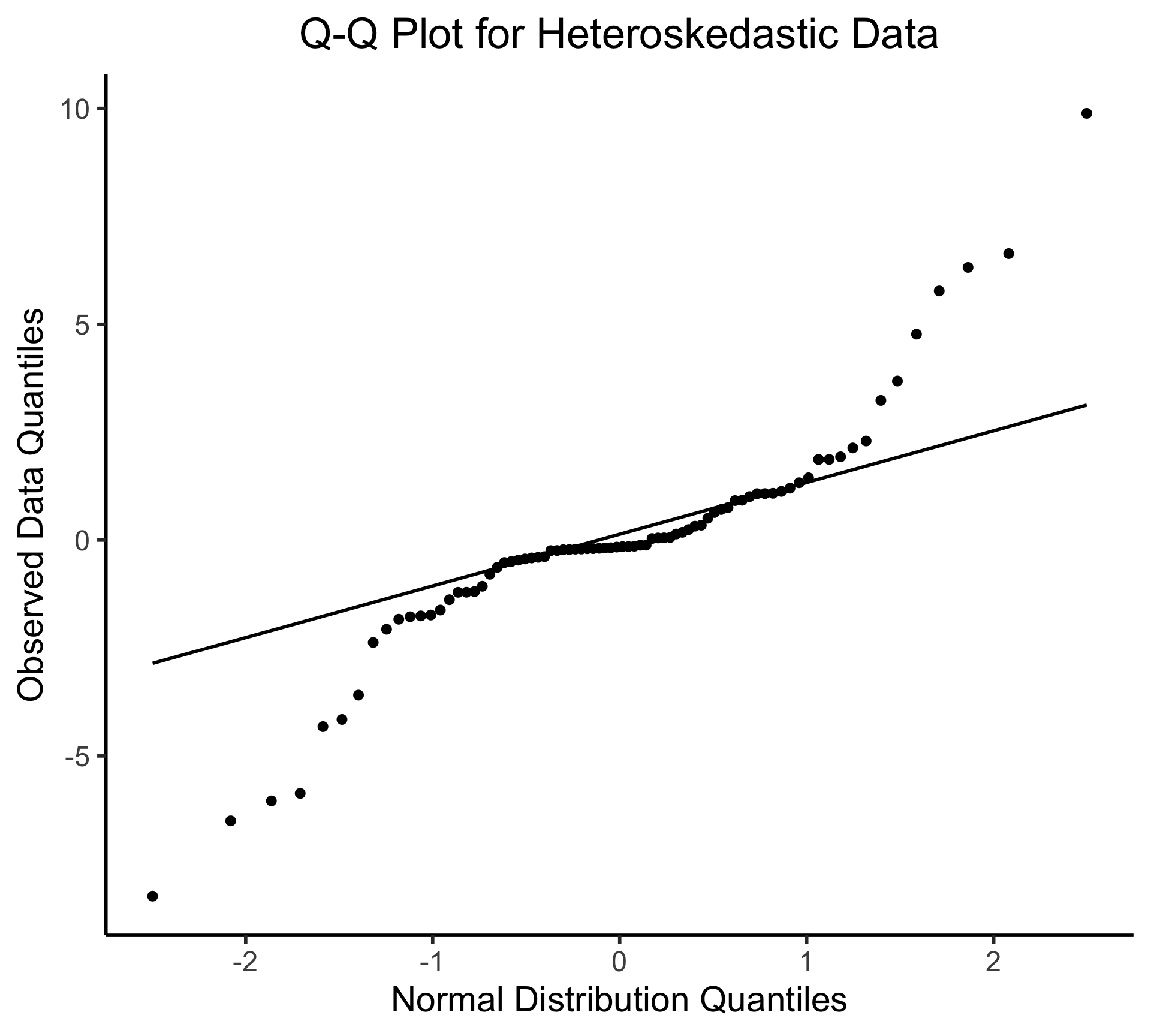
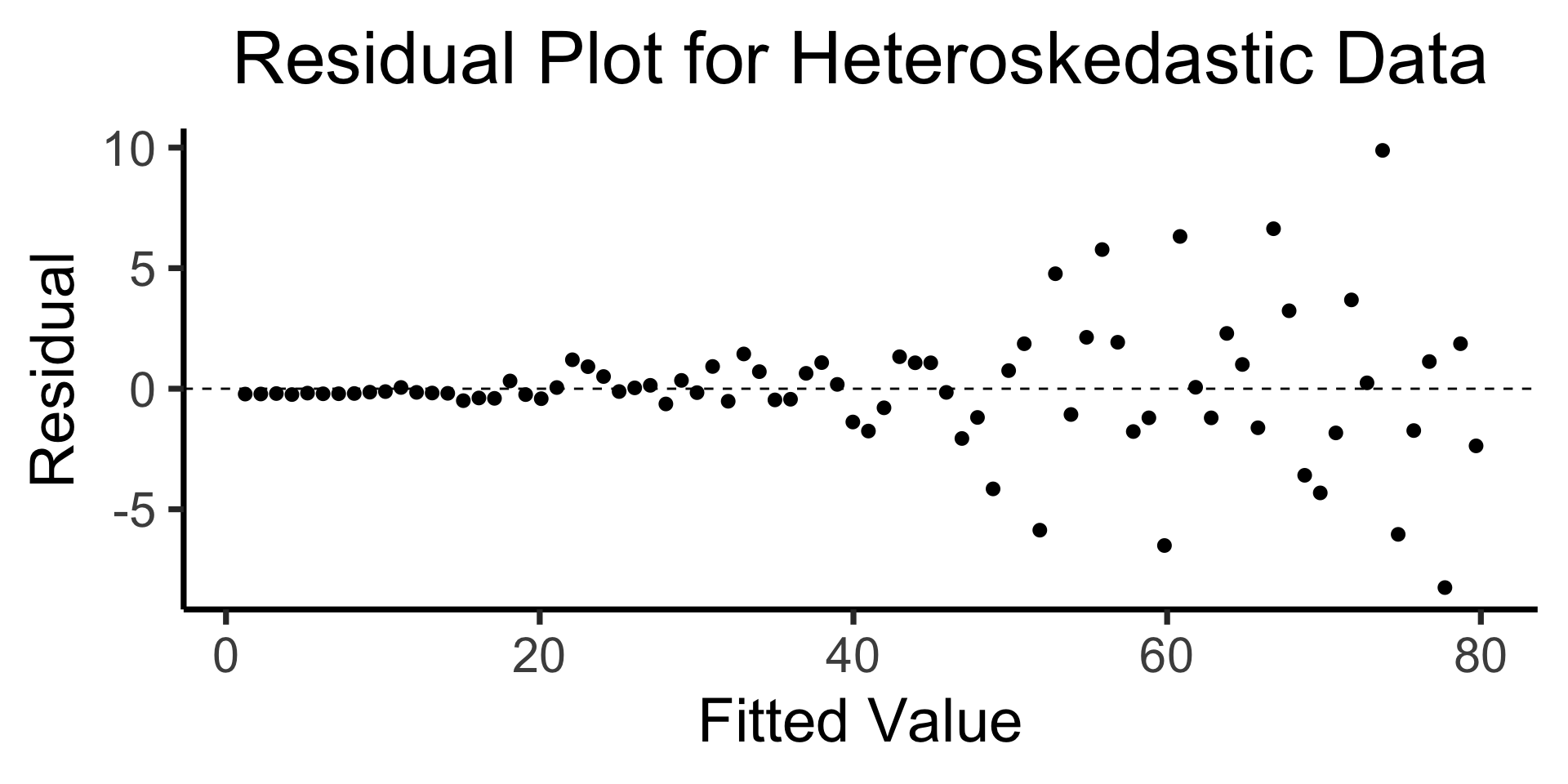
        title = "Residual Plot for Heteroskedastic Data",
        x = "Fitted Value",
        y = "Residual"
    )

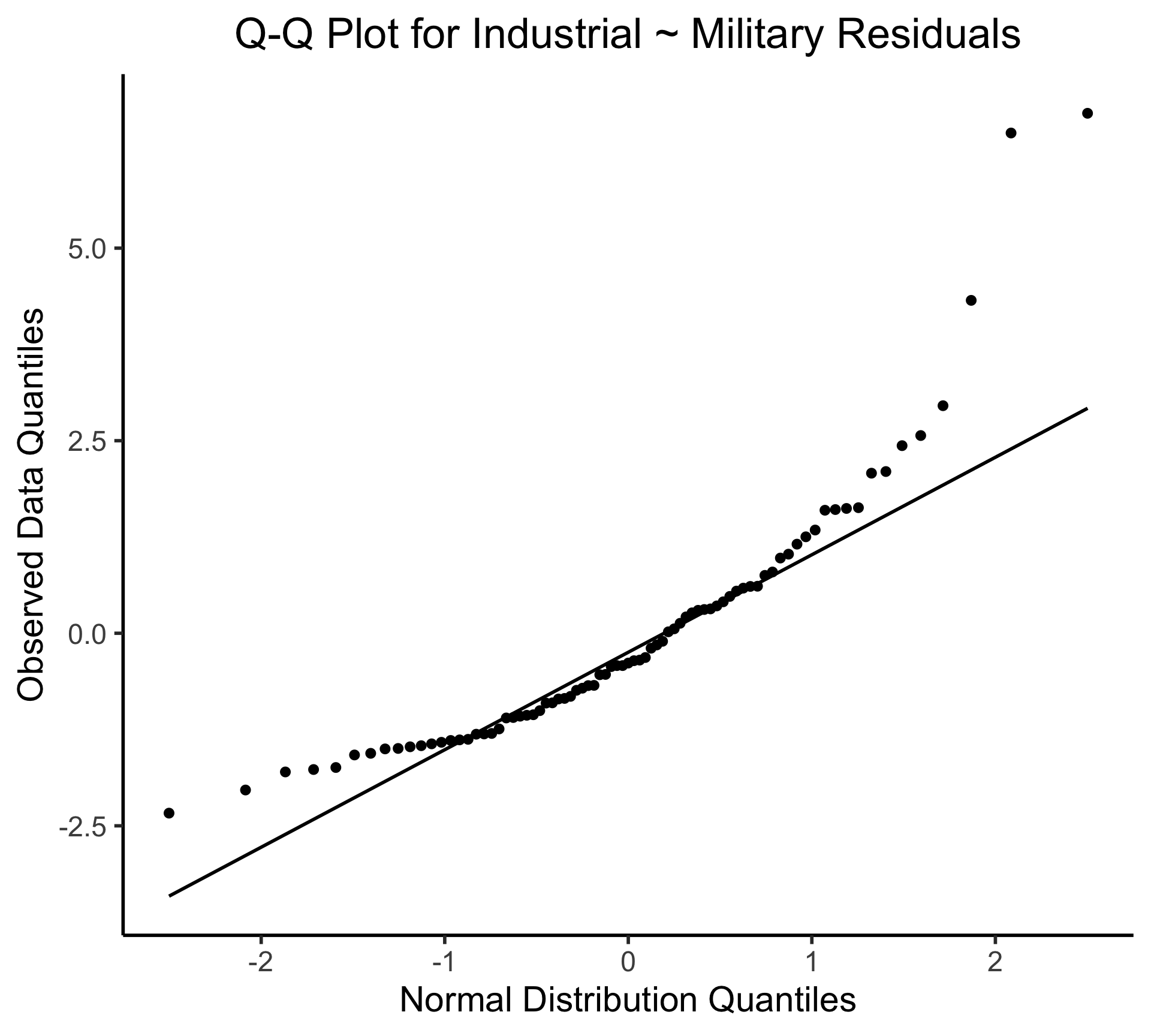
Q-Q Plot

  • If \((\widehat{y} - y) \sim \mathcal{N}(0, \sigma^2)\), points would lie on 45° line:
Code 
ggplot(df_het, aes(sample=.resid)) +
  stat_qq(size = g_pointsize/2) + stat_qq_line(linewidth = g_linewidth) +
  dsan_theme("half") +
  labs(
    title = "Q-Q Plot for Heteroskedastic Data",
    x = "Normal Distribution Quantiles",
    y = "Observed Data Quantiles"
  )

Code 
ggplot(gdp_resid_df, aes(sample=.resid)) +
  stat_qq(size = g_pointsize/2) + stat_qq_line(linewidth = g_linewidth) +
  dsan_theme("half") +
  labs(
    title = "Q-Q Plot for Industrial ~ Military Residuals",
    x = "Normal Distribution Quantiles",
    y = "Observed Data Quantiles"
  )

Multiple Linear Regression

  • Notation: \(x_{i,j}\) = value of independent variable \(j\) for person/observation \(i\)
  • \(M\) = total number of independent variables

\[ \widehat{y}_i = \beta_0 + \beta_1x_{i,1} + \beta_2x_{i,2} + \cdots + \beta_M x_{i,M} \]

  • \(\beta_j\) interpretation: a one-unit increase in \(x_{i,j}\) is associated with a \(\beta_j\) unit increase in \(y_i\), holding all other independent variables constant

Visualizing Multiple Linear Regression

(ISLR, Fig 3.5): A pronounced non-linear relationship. Positive residuals (visible above the surface) tend to lie along the 45-degree line, where budgets are split evenly. Negative residuals (most not visible) tend to be away from this line, where budgets are more lopsided.

Interpreting MLR

Code 
mlr_model <- lm(sales ~ TV + radio + newspaper, data=ad_df)
print(summary(mlr_model))

Call:
lm(formula = sales ~ TV + radio + newspaper, data = ad_df)

Residuals:
    Min      1Q  Median      3Q     Max 
-8.8277 -0.8908  0.2418  1.1893  2.8292 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept)  2.938889   0.311908   9.422   <2e-16 ***
TV           0.045765   0.001395  32.809   <2e-16 ***
radio        0.188530   0.008611  21.893   <2e-16 ***
newspaper   -0.001037   0.005871  -0.177     0.86    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.686 on 196 degrees of freedom
Multiple R-squared:  0.8972,    Adjusted R-squared:  0.8956 
F-statistic: 570.3 on 3 and 196 DF,  p-value: < 2.2e-16
  • Holding radio and newspaper spending constant…
    • An increase of $1K in spending on TV advertising is associated with
    • An increase in sales of about 46 units
  • Holding TV and newspaper spending constant…
    • An increase of $1K in spending on radio advertising is associated with
    • An increase in sales of about 189 units

But Wait…

Code 
print(summary(mlr_model))

Call:
lm(formula = sales ~ TV + radio + newspaper, data = ad_df)

Residuals:
    Min      1Q  Median      3Q     Max 
-8.8277 -0.8908  0.2418  1.1893  2.8292 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept)  2.938889   0.311908   9.422   <2e-16 ***
TV           0.045765   0.001395  32.809   <2e-16 ***
radio        0.188530   0.008611  21.893   <2e-16 ***
newspaper   -0.001037   0.005871  -0.177     0.86    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.686 on 196 degrees of freedom
Multiple R-squared:  0.8972,    Adjusted R-squared:  0.8956 
F-statistic: 570.3 on 3 and 196 DF,  p-value: < 2.2e-16
Code 
lr_model <- lm(sales ~ newspaper, data=ad_df)
print(summary(lr_model))

Call:
lm(formula = sales ~ newspaper, data = ad_df)

Residuals:
     Min       1Q   Median       3Q      Max 
-11.2272  -3.3873  -0.8392   3.5059  12.7751 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 12.35141    0.62142   19.88  < 2e-16 ***
newspaper    0.05469    0.01658    3.30  0.00115 ** 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 5.092 on 198 degrees of freedom
Multiple R-squared:  0.05212,   Adjusted R-squared:  0.04733 
F-statistic: 10.89 on 1 and 198 DF,  p-value: 0.001148
  • MLR results can be drastically different from SLR results, because of correlations (next slide)
  • This is a good thing! It’s how we’re able to control for confounding variables!

Correlations Among Features

Code 
cor(ad_df |> select(-id))
                  TV      radio  newspaper     sales
TV        1.00000000 0.05480866 0.05664787 0.7822244
radio     0.05480866 1.00000000 0.35410375 0.5762226
newspaper 0.05664787 0.35410375 1.00000000 0.2282990
sales     0.78222442 0.57622257 0.22829903 1.0000000
  • Observe how \(\text{cor}(\texttt{radio}, \texttt{newspaper}) \approx 0.35\)
  • In markets where we spend more on radio our sales will tend to be higher…
  • Corr matrix \(\implies\) we spend more on newspaper in those same markets…
  • In SLR which only examines sales vs. newspaper, we (correctly!) observe that higher values of newspaper are associated with higher values of sales…
  • In essence, newspaper advertising is a surrogate for radio advertising \(\implies\) in our SLR, newspaper “gets credit” for the association between radio and sales

Another MLR Superpower: Incorporating Categorical Vars

(Preview for next week)

\[ Y = \beta_0 + \beta_1 \times \texttt{income} \]

Code 
credit_df <- read_csv("assets/Credit.csv")
credit_plot <- credit_df |> ggplot(aes(x=Income, y=Balance)) +
  geom_point(size=0.5*g_pointsize) +
  geom_smooth(method='lm', formula="y ~ x", linewidth=1) +
  theme_dsan() +
  labs(
    title="Credit Card Balance vs. Income Level",
    x="Income ($1K)",
    y="Credit Card Balance ($)"
  )
credit_plot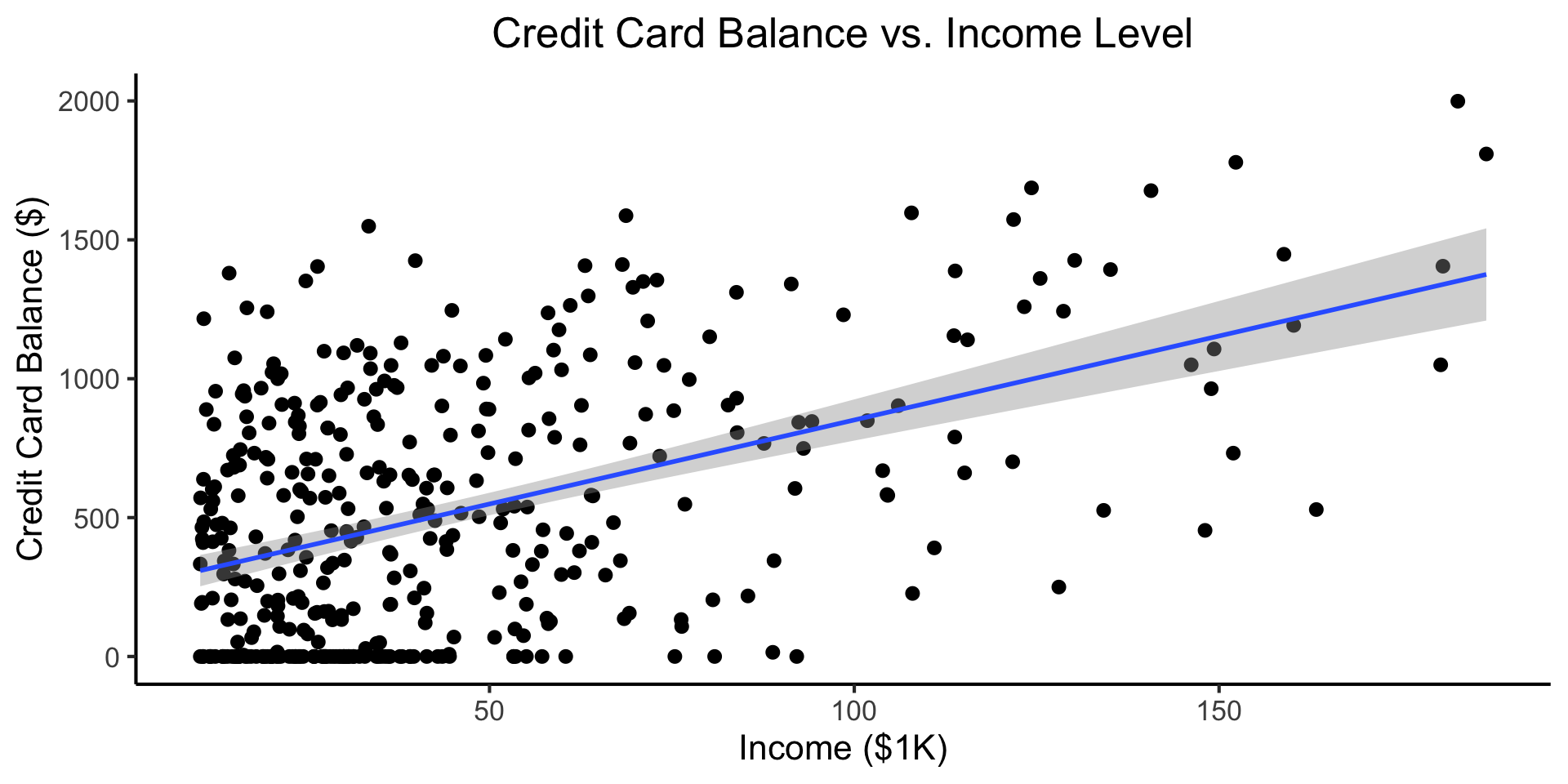

\[ \begin{align*} Y = &\beta_0 + \beta_1 \times \texttt{income} + \beta_2 \times \texttt{Student} \\ &+ \beta_3 \times (\texttt{Student} \times \texttt{Income}) \end{align*} \]

Code 
student_plot <- credit_df |> ggplot(aes(x=Income, y=Balance, color=Student)) +
  geom_point(size=0.5*g_pointsize) +
  geom_smooth(method='lm', formula="y ~ x", linewidth=1) +
  theme_dsan() +
  labs(
    title="Credit Card Balance vs. Income Level",
    x="Income ($1K)",
    y="Credit Card Balance ($)"
  )
student_plot

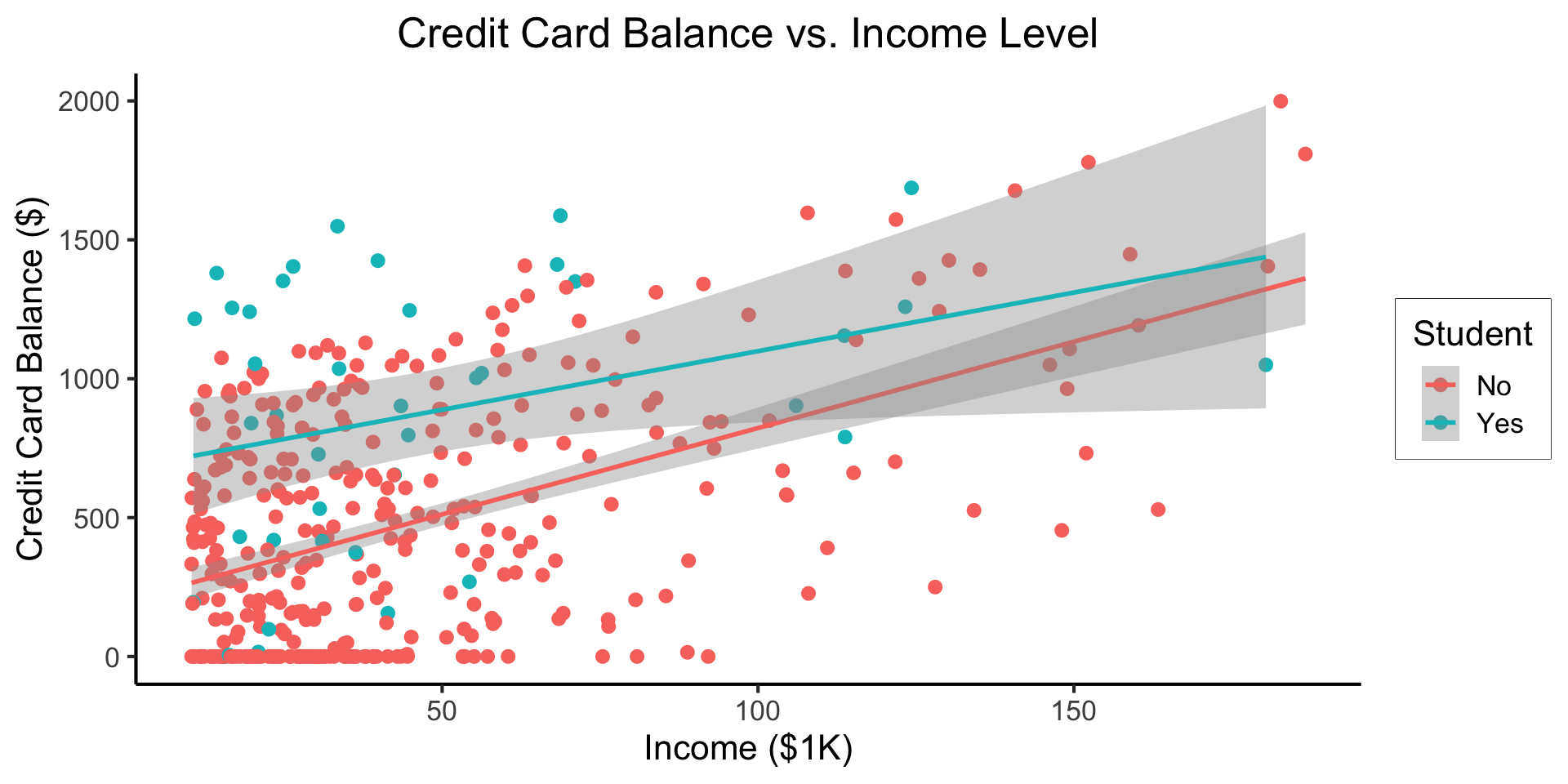
  • Why do we need the \(\texttt{Student} \times \texttt{Income}\) term?
  • Understanding this setup will open up a vast array of possibilities for regression 😎

References

Gelman, Andrew, and Jennifer Hill. 2007. Data Analysis Using Regression and Multilevel/Hierarchical Models. Cambridge University Press.